大气次声源定位算法及误差分析
尚楚翔,滕鹏晓,吕 君,杨 军,程 巍
(1.中国科学院声学研究所,北京100190;2.中国科学院大学,北京101408)
0 引 言
自然事件和人类活动会伴有次声信号产生。大气中的次声源主要包括3种[1]:人为制造的脉冲信号;陨石、火山喷发、地震等自然灾害;对流层中的大气扰动。由于大气层中存在温度和风向的分层结构,次声因其频率低、衰减小的特点,可以在大气中形成次声波导,传播上千千米而没有明显的能量损失[2],因此逐渐成为陨石、火山、核爆炸次声源定位的有效技术和实用方法。
文献[2-3]中根据已有的地震探测技术,提出逐步多通道相关方法(Progressive Multi-channel Correlation Method, PMCC)。通过次声信号检测方法和声达时间差(Time Difference of Arrival, TDOA)算法,可以计算出不同频段下次声波到达阵列的方位角和俯仰角。1996年,全面禁止核试验条约组织(Comprehensive Nuclear Test Ban Treaty Organization, CTBTO)成立,构建了国际监测系统(International Monitoring System, IMS),将次声作为核爆炸监测定位和当量估计的手段之一。IMS在全球设有60个次声监测站,保证任何位置发生当量大于1 kt以上的核爆炸至少能被2个监测站探测到,并使用PMCC方法对其定位。每个监测站采用4元次声阵列,阵列形状为中心一点,其余三点组成三角形[4]。1996年,谢金来[5-6]建立了中国科学院声学研究所核爆炸次声波监测系统,包括北京香山次声站、昆明次声站和杭州次声站。监测系统采用4元方阵,实现了四点定向、两阵定位的次声监测网络。Kennett等[7]通过增加阵元数目解决了IMS中4元中心三角阵列对高频信号出现混叠现象的问题,此后监测站逐步升级为8元或9元阵列。次声阵列监测系统不仅可以在最优置信度、实时性和灵敏度三方面显著提高核爆炸监测能力,还可以用于全球环境、人为灾害和自然灾害的监测[6]。
目前,CTBTO成员国研究人员广泛采用两个或多个阵列的地理坐标及其测得的多个方位角,通过在地球坐标系上进行测绘,定位次声源的经纬度。由于在阵列布置时,各阵元无法保证高度一致,忽略阵元间的海拔高度差,方位角的计算结果会存在一定的误差。本文基于最小二乘法,通过分析PMCC方法的主要流程,确定其次声源定位的主要误差来源,推导了在考虑和忽略阵元间高度差时计算次声波入射角的方法,针对特定阵型仿真模拟实现各方向入射次声波的计算误差可视化,研究最大海拔高度差和入射角计算误差之间的关系,并讨论了入射角的计算误差对后续定位的影响。
1 理论模型
PMCC方法主要包含次声信号检测方法和定位算法。其中定位算法采用TDOA算法,包括时间延迟估计(Time Delay Estimation, TDE)和基于时延的定位方法两部分。次声波在大气远距离传播过程中,不同频率的声波路径存在差异,到达阵列的入射角度不同[8],因此在定位前会先将各阵元的接收信号通过多个带通滤波器进行分频处理,以实现对不同频率次声波的定位计算。
1.1 时间延迟估计
TDE方法大致可包括最小均方(Least Mean Square, LMS)自适应滤波器法、自适应特征值分解法、声学传递函数比法等[9]。PMCC方法采用广义互相关(Generalized Cross- Correlation, GCC)[10]算法估计次声信号到达阵元的时间延迟。其原理相当于将接收信号进行前置滤波,适当消除噪声及干扰的影响后再进行相关运算,取其峰值进行时延估计,以提高时延估计的精度,具体流程如图1所示。图1中FFT表示快速傅里叶变换,IFFT表示快速傅里叶逆变换。
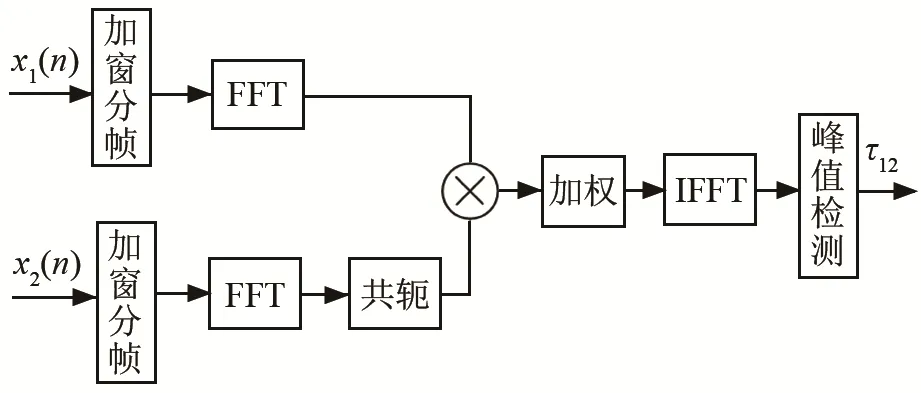
图1 广义互相关估计时延流程图Fig.1 Flow chart of generalized cross-correlation estimation of time delay
对于两个阵元接收到的信号x1(n)和x2(n),简化模型后可以表示为
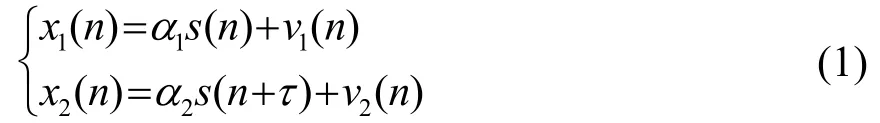
其中:s(n)为次声源信号,αi(i=1,2)表示次声信号到达阵元i的衰减系数,vi表示阵元i处的噪声信号。假设噪声信号与声源信号互不相关,噪声信号之间互不相关,互功率谱表示为
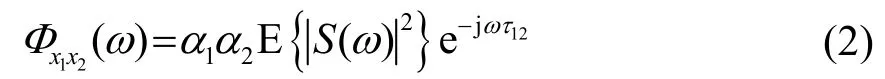
广义互相关定义为
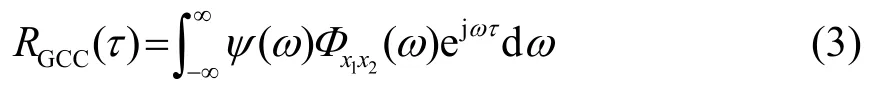
其中:ψ(ω)为加权函数,相当于前置滤波作用。文献[10]给出了多种通用的加权函数,PMCC方法主要使用HB(Hassab-Boucher)加权函数,其表达式为
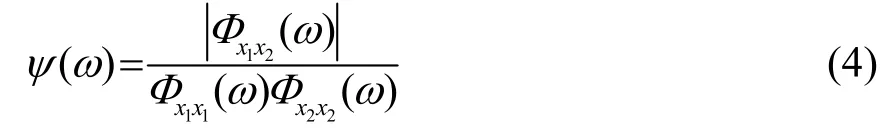
在实际应用中,使用信号频谱相乘估计功率谱,相关函数的最大峰会被弱化,同时噪声的相关性也会对结果产生影响。因此布置次声阵列通常选择背景噪声较小的位置,并且较大的阵元间距可以减小噪声相关性。
1.2 信号一致性阈值检测
目前CTBTO主要采用8元或9元阵列构建IMS监测站,由大尺寸的5元阵列嵌套小尺寸的3元或4元阵列组成。根据次声波长,阵元间距通常设定在1~3 km。较大的阵元间距可以减少空间噪声的相关性,提高广义互相关加权的滤波性能。同时可以增加声波到达阵元的时延,减小读取时延数据的测量误差对后续定位的影响。但阵元间距太大会使信号本身的互相关性下降,并且当阵元间距超过信号高频部分的半波长时,时延计算会出现空间混叠现象。可以看作两个阵元接收了不同周期内的高频信号,互相关函数会出现多个峰值,导致时延估计错误。
次声阵列Rn的任意3元子阵列(i,j,k)接收次声源信号的时延满足闭合时间关系:

由于背景噪声的相位具有随机性,并且读取时延数据存在测量误差,闭合时间关系无法严格满足。修正闭合时间关系更改为[11]
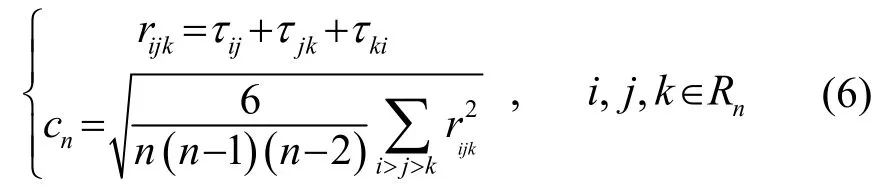
当阵列的修正闭合时间关系在阈值cthreshold范围内,说明阵元位置有效,否则说明某阵元位置干扰过大导致时延计算出现了较大误差。
为检测次声源信号并且避免高频信号出现混叠,检测过程会从小尺寸的3元阵列出发,逐步扩大阵型以提高计算精度。这种方式体现PMCC方法的逐级性,如图2所示。
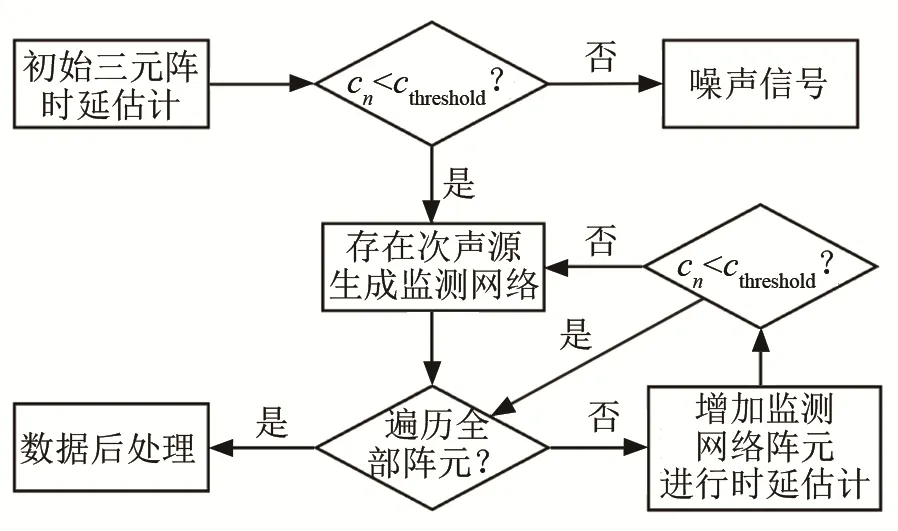
图2 PMCC方法的逐级检测Fig.2 Progressive detection by PMCC method
在监测过程中,需先排除连续零信号的传声器。当初始三元阵的接收信号时延满足修正闭合时间关系时,说明存在次声源,生成次声源监测子网络。逐个添加其他阵元,计算子网络的修正闭合时间关系并进行阈值判断,如果满足阈值范围则保留该阵元。遍历全部阵元后利用监测网络进行后续定位。
1.3 基于时延的定位方法
在获取不同频率次声信号到达各阵元的时间延迟后,可通过几何定位法或目标函数搜索法计算入射角。考虑到次声远距离传播的路径远大于阵列尺寸,声波到达阵列可视为平面波,入射角采用最小二乘法利用多通道时延进行计算。
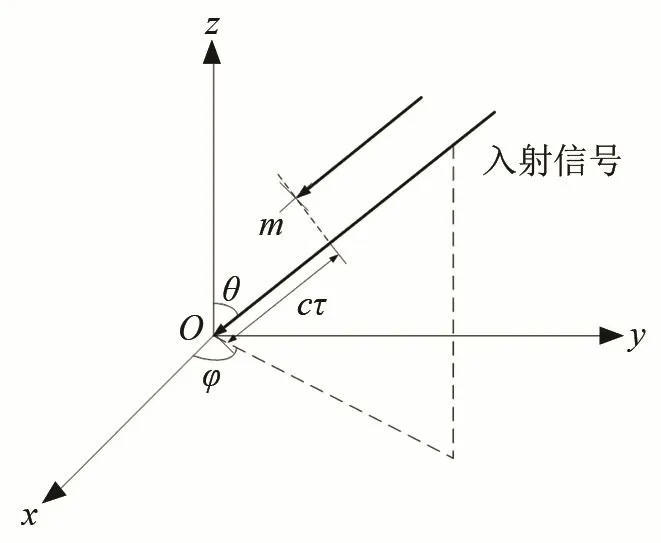
图3 任意阵列示意图Fig.3 Schematic diagram of arbitrary array
图3为任意阵列示意图。设入射信号方向为r=-[sinθcosφ,sinθsinφ,cosθ],其中方位角为φ(与x轴夹角),俯仰角为θ(与z轴夹角);阵元m的坐标为pm=(xm,ym,zm);c表示当地声速;τij表示阵元i相对于阵元j的延迟,正值表示信号先到阵元j、后到阵元i,τji可以表示为[12]
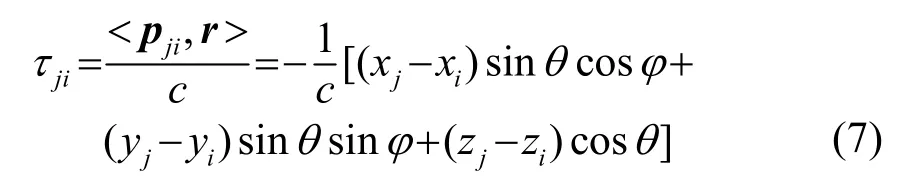
在实际测量中,阵元的地理坐标、采集设备和环境因素都有可能造成式(7)不严格相等,用误差表示为
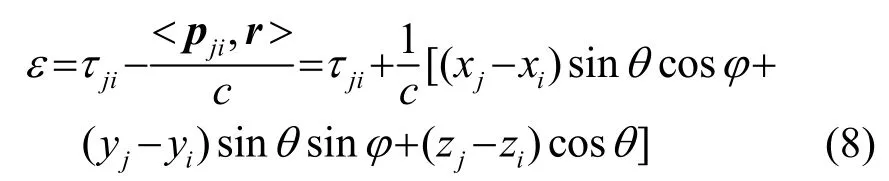
n个阵元的误差线性方程组可写为
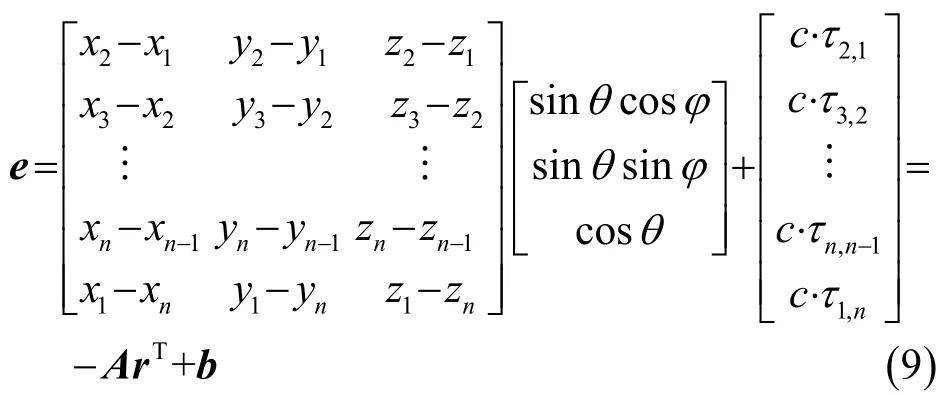
其中:e为误差向量,A为位置矩阵,b为声程差向量。在最小二乘意义下,估计误差的模的平方和

式(10)取最小值,可得到:
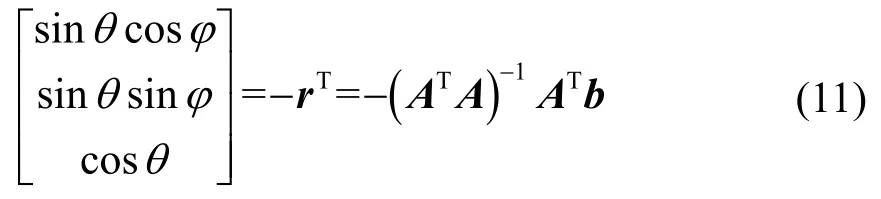
视速度V是表示次声信号的重要参数,由本地声速和俯仰角决定:

为了进一步滤除干扰信号,在时频域对计算结果进行聚类。
接收信号经过连续时间窗和分频处理后,通过时延定位可以得到由独立单元组成的时频图[13],每个独立单元成为聚类的检测点,如图4(a)所示。每个检测点Pi由时间ti、频率fi、视速度Vi和方位角φi表示,应用权重欧几里得距离表示相邻时间窗或频带之间检测点的距离[11]:
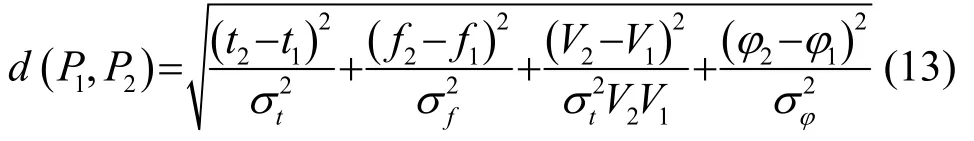
其中:σ表示对应参数的权值。设定阈值dmax,当时频图中两个相邻检测点的距离在阈值范围内,这两个检测点同属于一类信号。当类中检测点数量大于建立族所需要的最小数目时,建立一个PMCC族。图4(a)为聚类前的时频图,灰色检测点距离相邻的黑色检测点较远,在进行聚类后形成只包含黑色检测点的PMCC族,如图4(b)。建立PMCC族有效地排除了外界扰动信号,提高定位算法的抗干扰能力。
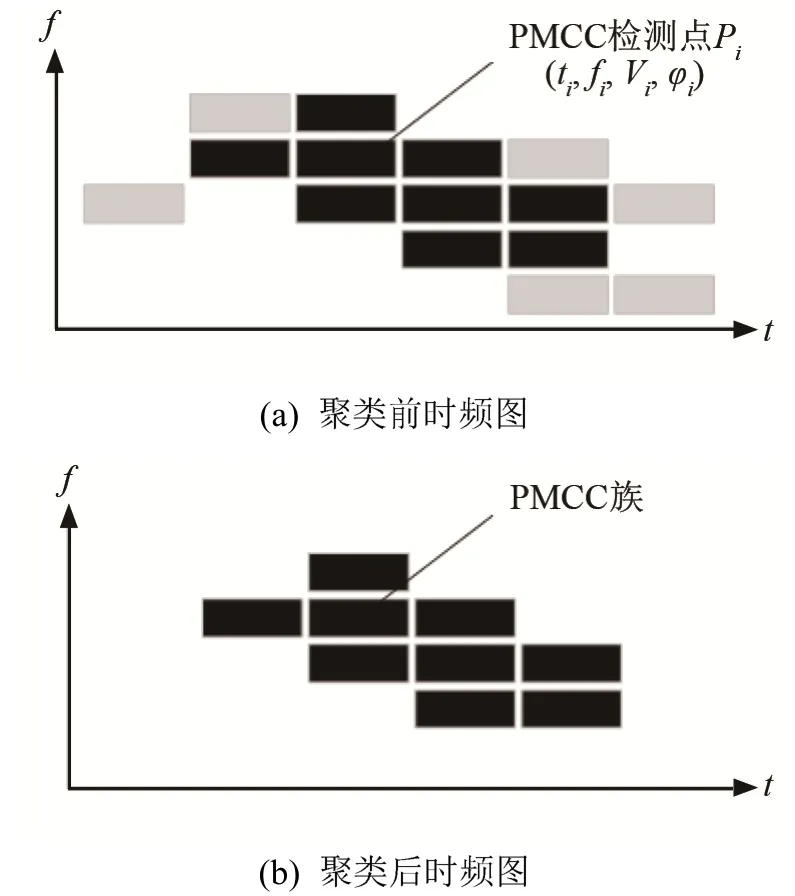
图4 聚类前后检测信号的变化Fig.4 Changes in detection signals before and after clustering
2 误差分析
在实际应用中,阵元的地理位置使用经纬度表示,不考虑其海拔高度,阵元m的坐标取为pm=(xm,ym)。此时式(9)中A变为n×2维矩阵:
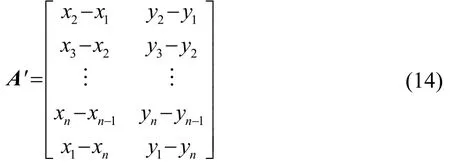
此时误差向量表示为
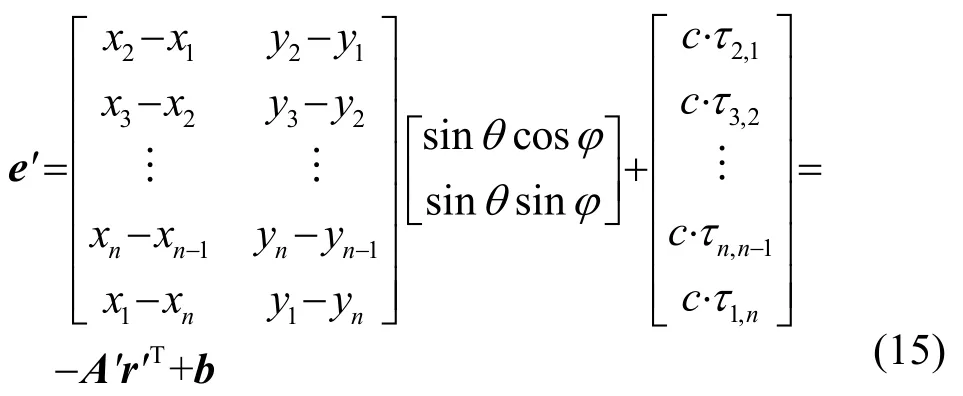
同样利用最小二乘法得到入射角度:
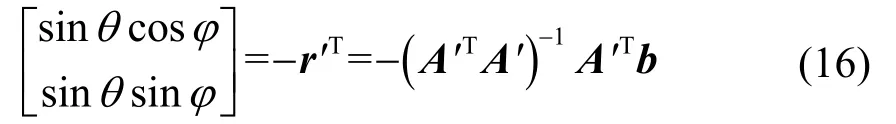
显然,式(16)与式(11)的结果不完全相等,这是因为忽略阵元海拔高度差会影响入射角的计算结果。
仿真采用的4元次声阵列示意图如图5所示,阵元间距为1~3 km,最大海拔高度差为0.04 km。由于误差只与阵元位置坐标和信号入射角度有关,利用式(11)计算各方向次声信号到达各阵元的真实时延,同时是次声阵列采集到的时延。利用式(16)求解在该时延下的入射角,进而对比各方向的误差结果。可以预测,信号入射角度越接近垂直入射,阵元海拔高度差所产生的时延在总时延中所占的比例越大,忽略高度差所产生的误差也就越大。
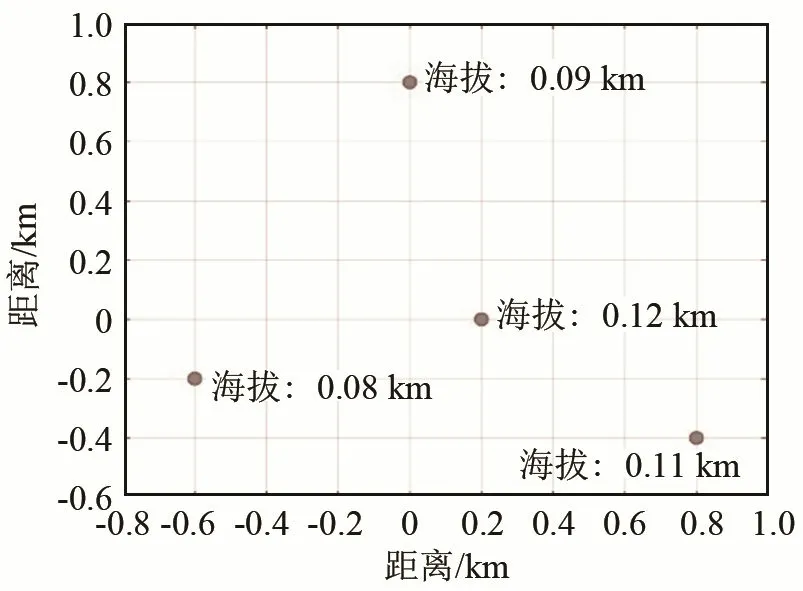
图5 仿真采用的中心一点其余三点组成三角形的4元次声阵列Fig.5 The triangular quaternary infrasound array composed of one element at the center plus other three elements
图6为取方位角0°~360°,步长1.8°的次声波入射到图5阵列,不考虑阵元高度差时产生的方位角误差。在图6(a)、6(b)中,当入射信号俯仰角接近0°,即信号接近垂直入射时,方位角误差极大,甚至相差180°,导致定位反向。随着俯仰角增加,方位角误差逐渐减小。接近水平入射的信号方位角误差范围可保证在2°以内。考虑到大气次声远距离传播到达阵列的俯仰角基本大于30°,将俯仰角取值范围改为30°到90°。图6(c)中,俯仰角为30°,方位角为90°或270°附近时存在误差极大值,与当前阵型构造有关。各方向方位角误差在3°以内。3°的方位角误差在次声传播水平距离500 km时,对应定位偏移误差约为25 km,次声传播水平距离1 000 km对应50 km的定位偏移误差。
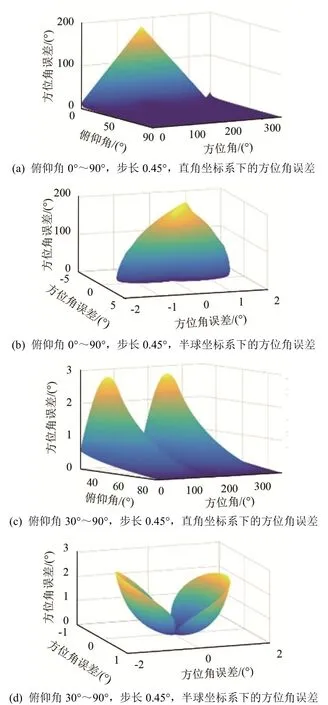
图6 不考虑阵元高度差时次声波入射到图5阵列产生的方位角误差Fig.6 The azimuth errors when the infrasound wave is incident to the array shown in Fig.5 without considering element height difference
图7为取方位角0°~360°,步长1.8°的次声波入射到图5阵列,不考虑阵元高度差时产生的俯仰角误差。由图7可见,各方向俯仰角误差全部在4°以内。随着俯仰角的增加,俯仰角误差逐渐减小。在入射信号方位角为344°、俯仰角为86°附近存在误差极大值,与当前阵型构造有关,不同阵型的极大值位置和大小不同。4°的俯仰角误差在俯仰角为57°、声速为344 m·s-1时,会产生14 m·s-1左右的视速度误差。
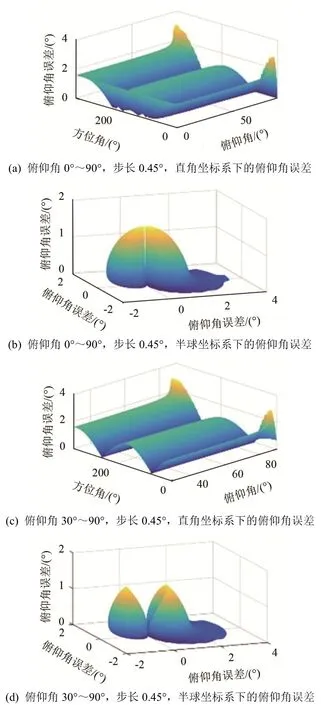
图7 不考虑阵元高度差时次声波入射到图5阵列产生的俯仰角误差Fig.7 The pitch angle errors when the infrasound wave is incident to the array shown in Fig.5 without considering element height difference
显然,入射角计算误差只取决于阵元海拔的相对高度差,而非绝对高度。仍然采用图5中的4元次声阵列,保持阵元水平位置不变,阵元的海拔高度服从0到设定最大海拔高度差值的均匀随机分布,在经过多次仿真试验后,可以得到对于同一入射角度的次声波,最大海拔高度差与入射角计算误差的关系,图8为方位角30°时平均俯仰角误差和平均方位角误差。随着阵元最大海拔高度差的增加,入射角计算误差呈线性增大。在最大海拔高度差为0.2 km的情况下,方位角误差可达到5°左右。对比图8(a)与图8(b)可以发现,当俯仰角较小时,方位角误差的增速高于俯仰角误差的增速。随着俯仰角的增加,俯仰角误差几乎没有影响,与图7相对应;但方位角误差会急剧减小,对应图6。
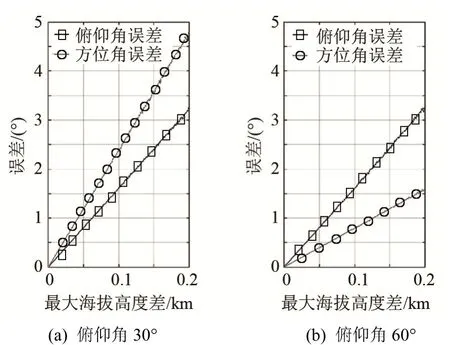
图8 方位角为30°时平均俯仰角误差和平均方位角误差Fig.8 The average pitch angle error and the average azimuth angle error with the azimuth angle of 30°
在忽略阵元海拔高度差的情况下,入射信号俯仰角为0°时,方位角误差最大,俯仰角误差存在极大值。随着俯仰角的增加,误差逐渐减小。次声阵列的阵型会对特定的入射方向产生误差极大值。随着阵元间最大海拔高度差的增加,入射角计算误差呈线性增大趋势。对于仿真的4元中心三角阵型,在限定入射方向与最大海拔高度差后,计算误差均可保持在5°以内,但由于次声传播距离较远,5°的入射角误差水平偏移距离相当于水平传播距离的9%,视速度误差可达到18 m·s-1左右。
3 结 论
本文依据PMCC方法,分析了基于HB加权的广义互相关时间延迟估计算法、信号一致性阈值检测方法和基于最小二乘法的平面波时延定位方法,确定了忽略阵元间的海拔高度差是PMCC方法产生误差的主要原因。推导了在忽略阵元间高度差的情况下次声波入射角的计算方法。通过假设存在高度差的4元中心三角阵型,对各方向入射声波因忽略阵元间海拔高度差而产生的误差进行模拟与分析。同时在假设阵型水平位置不变的情况下,讨论了最大海拔高度差与计算误差的关系。结果表明,在次声远距离传播的条件下,忽略阵元间的海拔高度差对后续定位误差有较大影响,PMCC定位次声源时需要考虑阵元海拔高度差的影响。

