船用离心风机壳体振动噪声优化研究

张建华，楚武利，杨晓彤，张晶辉

(1.西安航空学院飞行器学院，陕西西安710129；2.西北工业大学动力与能源学院，陕西西安710072；3.先进航空发动机协同创新中心，北京100191；4.中国航发西安航空发动机有限公司，陕西西安710021)

0 引 言

船用离心风机一般在高温、高湿且较为密闭的环境下运行。根据GB/T 11865《船用离心通风机》[1]的国家标准，船用离心风机不仅要满足普通风机的安装和运行要求，还要满足低振动烈度、噪声辐射运行要求。当风机用于舱室内通风换气时，风机的出口连接长管道，此时风机的气动噪声不能直接传递到外界，流体激励风机机壳引发的壳体表面振动，振动激发产生的结构振动噪声则成为主要噪声。事实上风机的非定常流动诱发的噪声属于流固干涉噪声(流体激励力对壳体振动引发的在空气中传播的振动噪声)，叶轮和蜗壳是弹性体结构，尤其在大型风机中蜗壳的振动不可忽略[2]。离心风机的叶轮内部流动诱发壳体振动的振动噪声鲜有学者研究，但这类噪声问题在大型风机系统中也显得尤为突出，目前叶轮内部流动诱发蜗壳壳体振动噪声的研究仅限于计算方法。20世纪末，Koopmann等[2]首次提出了一种基于边界元(Boundary Element Method, BEM)计算和实验测量相结合的预测方法。此方法将分离气动噪声，单独计算大型离心风机叶轮内部的非定常流动诱发的蜗壳壳体振动噪声，振动噪声计算所需的压力脉动通过实验获得；随后，Hwang 等[3]采用和文献[2]相同的方法成功预测了冰箱用压缩机的振动声辐射；21世纪初，蔡建成等[4]、Lu等[5]采用数值计算和实验相结合的方法，预测了工业用T9-19 No.4A离心风机蜗壳的振动声辐射。振动噪声研究的目的是获得振动噪声产生机理，提出有效的降噪方法。目前，结构减振方法非常引人注目，它实际上是通过修改受控对象的动力学特性参数使振动满足特定要求，不需要添加任何子系统的控制方法。而结构减振主要以结构优化为主，离心风机的蜗壳属于薄壁结构，而薄壁结构的振动辐射声功率是关于结构振动速度的二次型函数[6]，通过优化设计使得结构振动速度降低，则必能使其辐射的声功率在一定范围内降低。周正等[7]、Lu等[5]通过优化降低结构表面振动速度方法获得了降噪效果。然而，上述学者在预测壳体振动声辐射的计算中，将计算分为两个过程：(1) 以结构有限元法获得结构的振动速度；(2) 以声学边界元法获得结构的振动声辐射，计算过程较为繁琐，容易出错。因此，有必要采用振动、噪声同步计算的方法，减小计算过程中可能存在的误差。本文采用数值计算方法，给出一种基于振动噪声同步计算的振动噪声一体化优化方法，在保持壳体质量不变的前提下，有效地降低壳体振动声辐射。

1 数值计算模型

1.1 离心风机模型参数

以某船用离心风机为研究对象，该风机依据使用环境不同，分为两种安装状态：进出口开口和进出口连接有封闭长管道，本文所研究的风机处在第二种安装环境下，该风机具体参数见表1。

1.2 非定常流场计算

1.2.1 流场网格

叶轮出口不稳定流动对壳体壁面的周期性冲击是壳体振动的主要激励源。为了获得较为精确的振动激励源，风机内部的流动结构全部采用高质量的六面体结构化网格处理。由于风机计算模型较复杂，将风机整个计算域分成四个主要部分： 过渡段和进口管道计算域(包含深入叶轮内的轴向进气空腔区域)，翼型叶轮网格计算域、带有前后空腔的蜗壳整体网格计算域，节流阀和出口延伸段计算域。风机计算域的网格数如表2所示。

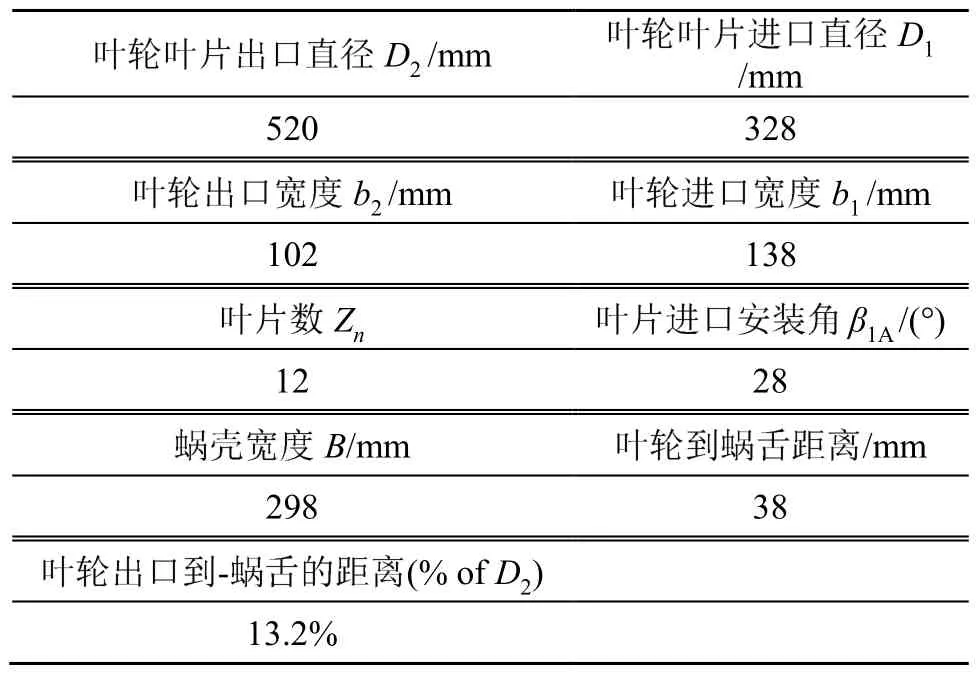
表1 风机参数Table 1 Parameters of centrifugal fan

表2 风机计算域的网格数Table 2 Grid numbers in the calculational domain of fan system

各计算域之间通过交界面(interface)相互连接，在转动域和静止域之间设定两个重要的转/静交界面：其一，与叶轮相连接的进口空腔和叶轮进口(进口-叶轮)交界面；其二，叶轮出口和蜗壳进口(叶轮-蜗壳)交界面。为了减小计算模型和样机的误差，网格划分过程中考虑了叶轮、过渡段厚度(2 mm)以及叶轮盖板厚度(轮盘厚度为3 mm，轮盖厚度为6 mm)、过渡段与叶轮进口径向间隙1mm，详细参数如图1所示。图2显示了风机的总压升系数和气动效率随流量的变化曲线，网格数增加一倍后，总压升基本保持不变，此曲线进一步证明了网格数超过2.8×106后，网格达到无关解(网格数量对计算结果没有影响)。

1.2.2 流场计算模型和边界条件

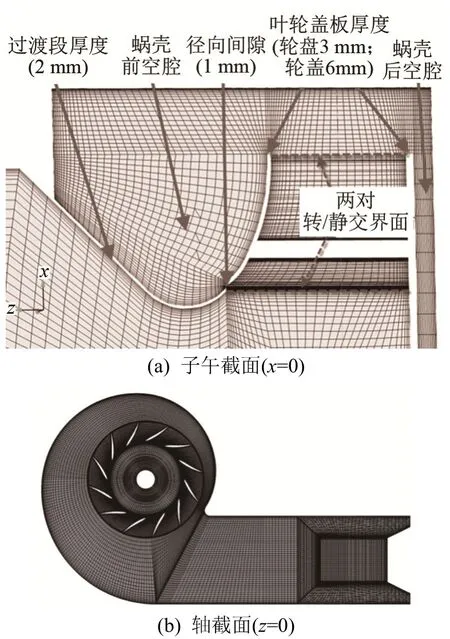
图1 风机网格截面图Fig.1 Surface mesh of blade and hub

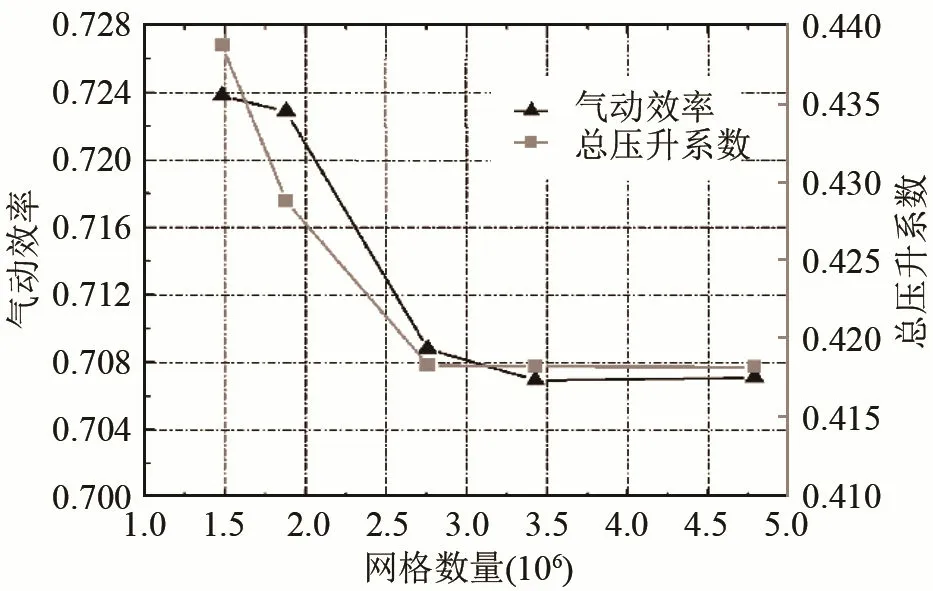
图2网格无关性验证Fig.2 Grid independence validation

基于商业软件ANSYS CFX求解连续方程、动量方程和标准k-ε湍流控制方程。各控制方程均采用有限元体积法离散。控制方程的空间离散采用高精度的高阶格式差分，非定常计算的时间推进格式为双时间步长全隐式格式，时间项使用二阶后向欧拉差分离散，一个耦合求解器[8]依照压力的耦合求解算法耦合求解连续方程和动量方程。定常流场以稳态解为初场，模拟设计点下最佳效率点(Best Efficiency Point, BEP)风机内部的非定常流动状况(本文的振动噪声的计算流量点)。非定常时间步设定：叶轮有12个叶片通道，每个通道给定30个时间步，叶轮转动一周分成360个时间步，即叶轮每转动1°消耗一个时间步长，每个时间步长为5.7089×10-5s，这个时间步长足够进行动态压力信号采集。计算结果显示，当叶轮转动5 400个时间步长，即转动15周后，设定的监测点达到稳定的周期性波动，此时判定计算收敛。

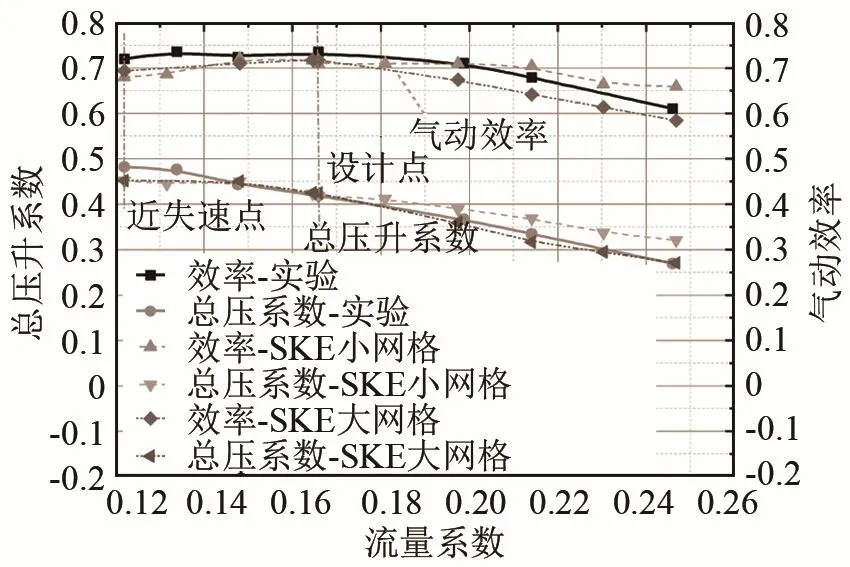
图3 风机气动性能曲线对比Fig.3 Comparison between numerical and experimental curves of fan aerodynamic performance

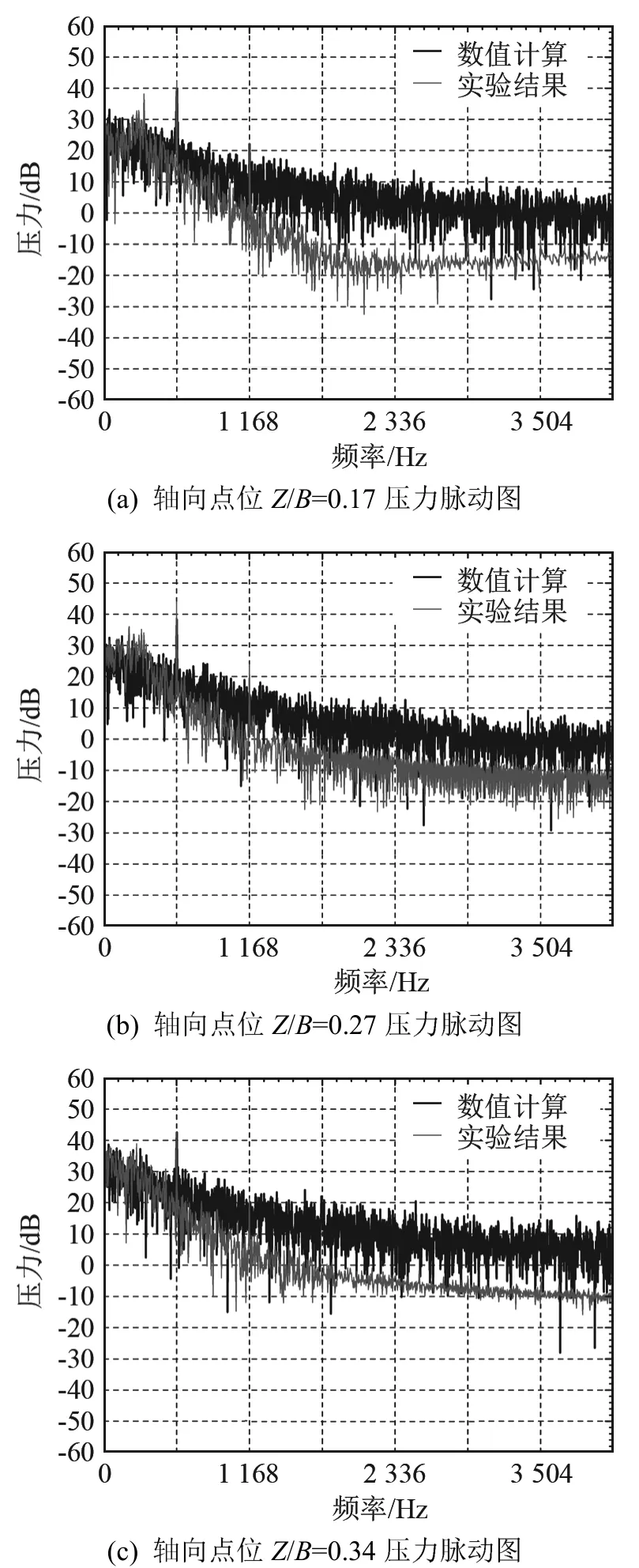
图4 监测截面1上三个轴向测量点的蜗壳壁P1截面上压力脉动频谱Fig.4 Power spectra of the pressure fluctuation on P1 section of volute wall measured at three axial measurement points

图3给出了风机气动性能数值和实验的对比曲线。在设计转速下(2 920 r·min-1)的最佳效率点(BEP)对应的流量为Q=3.361 kg·s-1(φ=0.166)和总压升PT=3182 Pa(ψ=0.420)。图4给出了蜗壳壁面P1截面叶轮出口点位压力脉动频谱图。测点分布和描述详见作者已发表文献[8]。在P01点位的所有的数值和实验测量频谱中，叶轮出口范围内(Z/B=0.07～0.36，Z为蜗壳到后板的距离，B为蜗壳轴向宽度)，叶片通过频率(Blade Passing Frequency, BPF)(对应基频584 Hz)处观察到明显的峰值。且在基频上，计算和实验吻合较好，这表明对于文中最为关注的基频噪声，噪声源计算模型是可靠的，详细实验和计算分析过程参考文献[8]。

1.3 振动噪声计算模型

1.3.1 振动噪声数学模型

定义振动表面声辐射的基尔霍夫(Kirchhoff)公式为[9]

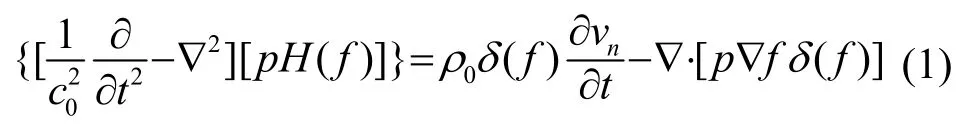
式中：p表示声压，nv表示振动的法向速度，H(f)为赫维赛德(Heaviside)函数，而δ(f)为狄拉克(Dirac)函数，方程右端第一项是由于振动表面排开流体体积产生的声音，是单极子源；方程右端第二项是结构处于其振动产生的声场中对声场的散射影响，为偶极子源。式(1)经过快速傅里叶变换后得到频域结构表面声辐射控制方程即基尔霍夫-亥姆霍兹(Kirchhoff- Helmholtz)方程为

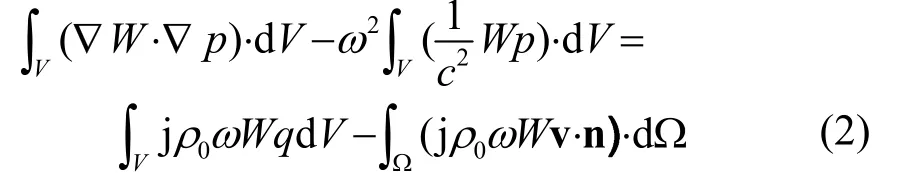
式中：W表示计权函数，q为声源项(式(1)中右端的所有项)。根据有限元理论获得结构振动表面离散点(结构网格节点)的声压，通过插值函数逼近得到其他结构节点声压，随后求得声功率值。

1.3.2 振动噪声数值计算过程

风机蜗壳壳体有限元模型采用Shell63单元构建。按照风机壳体厚度不同分为三个板块有：前板厚度TF、后板的厚度TB均为6 mm，壳体侧板的厚度TS为5 mm，如图5所示。基于表面四边形网格划分46 182个shell63单元。模型材料为钢，密度为ρ=7 800 kg·m-3，弹性模量E=2.06×1011 Pa，泊松比γ=0.3。振动边界约束条件为：蜗壳前板设定10个均匀分布的固定螺栓，蜗壳后板设定4个均匀分布的固定螺栓，所有螺栓的三个方向平动自由度为0，有限元网格详细描述参考文献[10]。针对壳体振动噪声，文中给出了具体的计算方法，计算流程如图6所示。根据振动激励源计算、振动计算、振动噪声数值计算将整个计算过程分为三个主要步骤：(1) 基于非定常流场计算获得振动激励源；(2) 基于构建的壳体结构有限元模型计算模态参与因子；(3)加载模态参与因子和振动激励源，基于振动噪声单向计算方法计算壳体振动声辐射，详细分析过程见参考文献[11]。

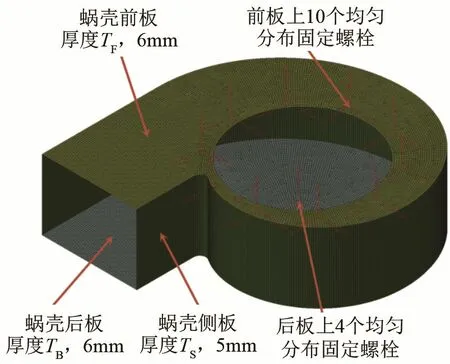
图5 蜗壳有限元模型Fig.5 FEM model of volute casing

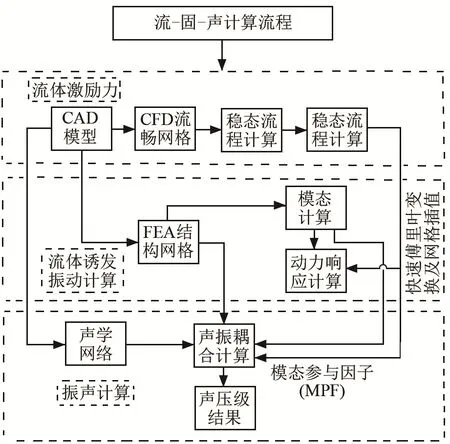
图6 振动噪声计算流程示意图Fig.6 The flow chart of numerical evaluation method for casing vibro-acoustic calculations

1.3.3 振动噪声计算数值验证

风机运行时，内部非定常流动激励机壳振动，机壳产生微小变形，然而其表面变形的位移量级远小于流体壁面边界层厚度，因此对于此类设备结构的振动噪声问题一般采用考虑流体脉动压力单向作用于薄壳体壁面，计算壳体振动在空气中辐射噪声时，忽略空气的反作用。Jiang等[12]对离心泵内部的非定常流动诱发振动问题的计算和实验结果验证了此方法的合理性。

定义总振级的公式为

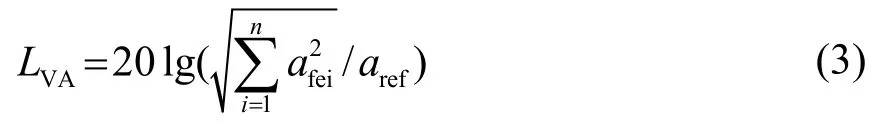
式中：aref=1×10-6m·s-2表示参考加速度值，afei表示频谱内单个频率的振动加速度有效值。

图7给出了各振动测点在20～3 000 Hz频率范围内总振级的计算和实验对比。从图7中可以看出绝大部分振动测点的计算和实验吻合良好，虽然少数测点(测点1、4、13)有限元计算结果和实验值误差较大，最大误差为15 dB，但是总体来说计算和实验误差控制在一个量级范围(20 dB)内，这与文献[5]中对T9-19 No.4A离心风机蜗壳振动的计算和实验所得的误差分析一致。这表明，本文所采用的振动噪声计算方法是合理且有效的。

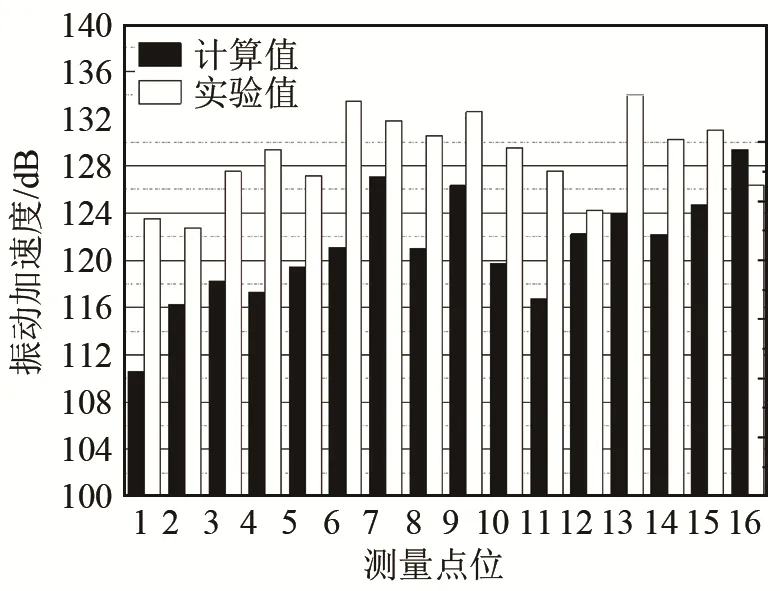
图7 振动加速度的计算值和实验值对比Fig.7 The comparison between calculated and tested amplitudes of vibration acceleration

2 振动噪声优化过程

2.1 振动噪声优化数学模型

对于开口域的噪声控制问题，目标函数一般选取外部辐射的声功率，此种方法已经被诸多学者所验证[13]。结构表面辐射声功率和外部激振力Fi、模态振型φi、频率放大因子βi之间的关系定义为[14]

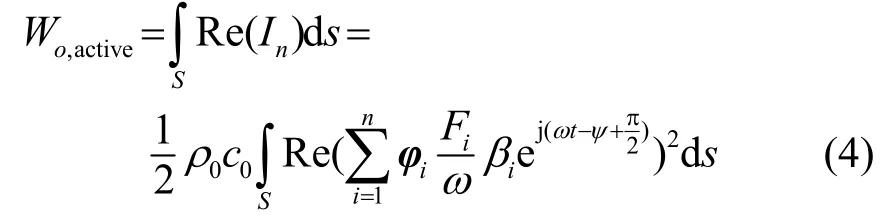
式中：Wo,active表示结构表面有功辐射声功率，Re(In)表示声强实部。当外加激振力Fi确定的情况下(流动激励力不变)，减小结构振型φi可以达到降噪的效果。结构的振型和固有频率取决于结构的几何形状、厚度分布、结构刚度以约束位置，当结构几何形状、结构刚度和约束位置一定时，可以通过控制结构厚度分布来改变结构的振型。由于风机蜗壳的厚度一般小于10 mm，我们将蜗壳板厚限制为4～10 mm。本部分优化的数学模型如下：

定义蜗壳表面辐射声功率(Kirchhoff Sound Power of Wall, Kirchhoff SPW)为目标函数Ws：

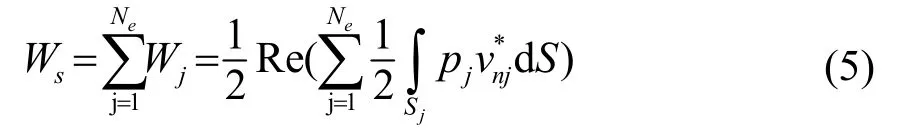
设计变量TF、TS、TB，约束条件为

声功率级定义为

式中：Wref表示参考声功率值，Wref=1×10-12W。

2.2 优化过程及分析

为了提高优化效率，文中采用了试验设计方法(Design of Experiment, DOE)和近似模型(Approximation Models, AM)相结合的方法来搜寻结构设计变量和目标函数之间的确定关系，为后面的优化提供基础数据和模型。蜗壳结构的振动噪声优化涉及多个程序的顺序启动，因此本文将多个不同的计算软件(UG、ANSA、Nastran、LMS)整合到多学科仿真优化平台Isight中，基于多学科多目标优化平台Isight完成风机蜗壳壳体振动噪声的优化过程。图8给出了Isight的集成示意图，从图中可以看出，优化过程主要分为3个步骤：(1) 基于DOE创建样本点设计空间(Design space)；此部分耗时最长，也是计算的中心环节。针对本文所研究的船用离心风机蜗壳，以各蜗壳板厚(前板TF、后板TB、侧板TS)为设计变量，每个设计变量给定5个水平，表3给出了各设计变量的水平分布。由于设计变量较少，在三个变量所构建的设计空间中采用全因子法进行样本点的采集，共采集125个样本点。对于每个样本点采用前文的振动噪声单向数值计算方法进行数值计算，获得各变量组合蜗壳结构表面的辐射声功率。(2) 基于步骤(1)中完成的样本点通过插值方法(RBF 近似模型，对于非线性问题最为有效)获取优化的近似数学函数。图9给出了近似模型的拟合精度，从图中可以看出近似拟合计算值和数值计算值基本重合，蜗壳表面辐射声功率(Kirchhoff SPW)的R2无限接近1，因而所构建的近似模型完全能替代实际的蜗壳表面辐射声功率、模型，用于后面的优化设计工作。(3) 基于步骤(2)得到的拟合函数，采用自适应模拟退火算法全局优化(Adaptive Simulated Annealing, ASA)获得优化解，以全局优化解为初值，通过混合整型序列二次规划局部寻优获得最优解。

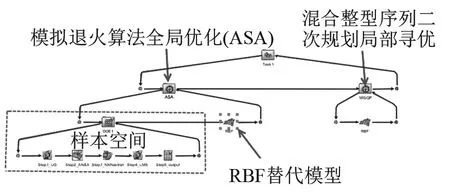
图8 Isight优化整合示意图Fig.8 The schematic diagram of Isight optimizing integration

表3 蜗壳各板厚设计参数的水平分布Table 3 The horizontal distributions of the design parameters of volute wall thickness (TF, TS and TB)

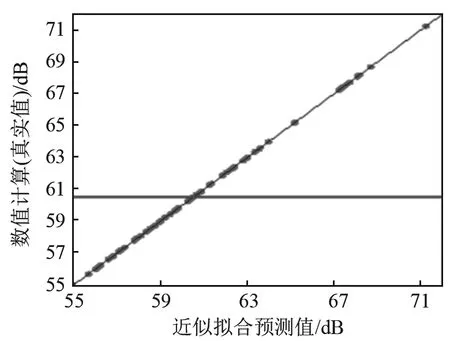
图9 蜗壳表面声辐射值拟合误差分析Fig.9 Analysis of fitting error

图10给出了设计变量(TF、TS、TB)和响应目标(蜗壳结构表面辐射声功率Kirchhoff SPW)之间的相关性系数分布。图10中的正值表示目标响应和设计变量之间的正比例关系，反之，为反比例关系；系数绝对值越接近1，相关性程度越高。从图10中可以看出，TS对响应相关性程度最高，其次是TF，再次是TB，TS、TB与辐射声功率成反比例关系，这表明TS、TB越大，辐射声功率越小。然而，图11蜗壳各板块的主效应图则显示，随着TF厚度增大蜗壳表面辐射声功率呈现先减小后增大趋势，当TF值为6.3 mm时，蜗壳辐射声功率最小；TB相对于TF则呈现相反的变化趋势，TB随着厚度的增加，蜗壳表面辐射声功率表现出先增大后减小的趋势；而TS随着厚度的增加，蜗壳表面辐射声功率值呈现直线下降趋势，但是当TS大于8.8 mm之后，蜗壳表面辐射声功率幅值基本上保持不变。以上分析表明，TF、TS、TB均存在最佳合理范围，这需要优化来获得最合理的TB，TS、TB值满足蜗壳表面辐射声功率值最小。图12给出了此类单目标优化的流程图。单目标优化采用模拟退火算法在样本空间内进行全局搜索，以前文的近似模型最优结果为初值，全局优化迭代了10 000步，耗时12 min；随后以ASA最优结果为初值采用混合整型序列二次规划(Mixed-Integer Squential Quadratic Programming,MISQP)进行局部寻优，此过程迭代了12步，耗时仅为数秒。

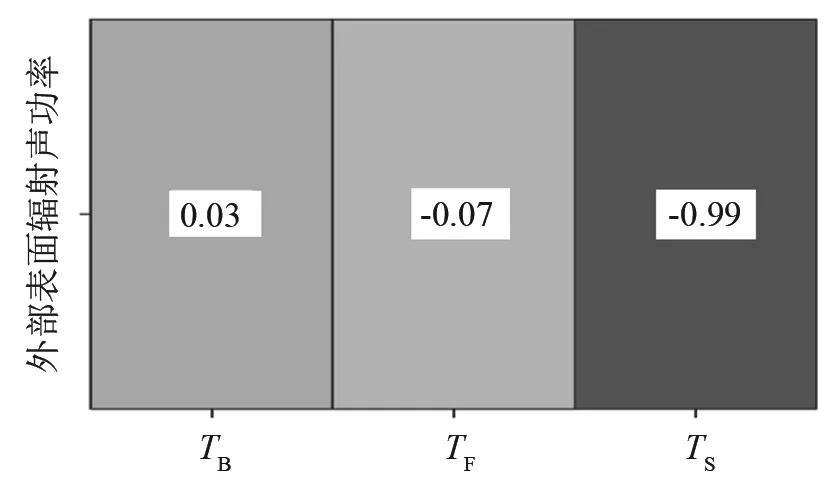
图10 壁厚设计参数和蜗壳结构表面辐射声功率的相关性分析Fig.10 The correlation analysis between the design parameters of volute wall and the acoustic power radiated from the surface of volute structure (Kirchhoff SPW)

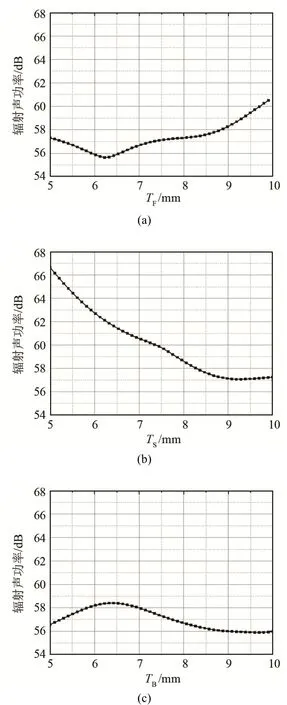
图11 蜗壳壁厚和辐射声功率关系Fig.11 The relationships between the volute wall thickness and Kirchhoff SPW

图12 单目标优化流程图Fig.12 The flow chart of the single-objective optimization(Kirchhoff SPW)

表4给出了保持质量不变的优化结果，若保持质量不变，蜗壳结构表面的辐射声功率也有较大程度的减弱，平均减弱了6.3 dB。由于工程上常用尺寸圆整或是近似厚度的钢板，因此设定蜗壳3个板厚度分别为TF=4.5 mm，TS=7.5 mm，TB=4 mm，经过数值计算得到蜗壳表面的辐射声功率为59.42 dB，厚度误差为1.26%，在许可范围内。图13的蜗壳结构表面的辐射声功率频谱也显示出，基频声功率幅值最为突出，优化明显地改善了蜗壳表面的基频辐射声功率，降低了6.23 dB。为了验证频率步长对声功率频谱尖峰处的数值影响，图14给出了以1 Hz为频率步长，频率波段在573～593 Hz之间的声功率频谱曲线。从图14中可以看出，基频处的声功率依然最为突出，优化后基频处的声功率值降低了6.03 dB。从图15和图16中基频下蜗壳表面以及不同截面的振动声辐射分布对比中可以分析出：优化使得蜗壳侧板靠近蜗舌附近的振动辐射声压大幅度减小，蜗壳其他区域的振动辐射声压也有不同程度的减弱，优化也改变了声辐射的指向性分布，在蜗壳后板一侧产生了非常明显的指向性。

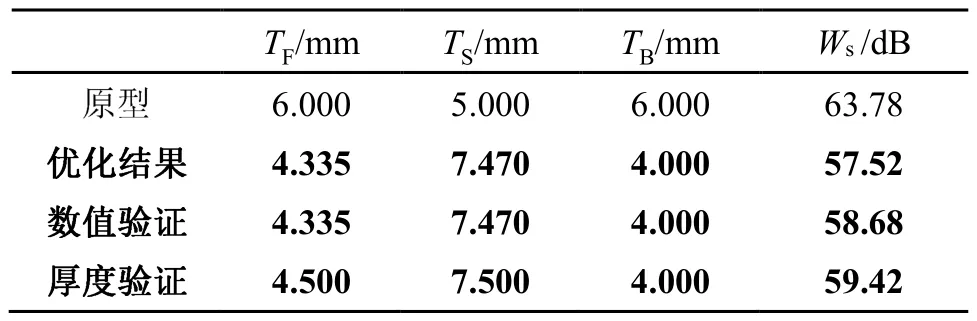
表4 蜗壳总质量不变的单目标优化结果Table 4 The single-objective optimization results while the volute total mass keeping constant

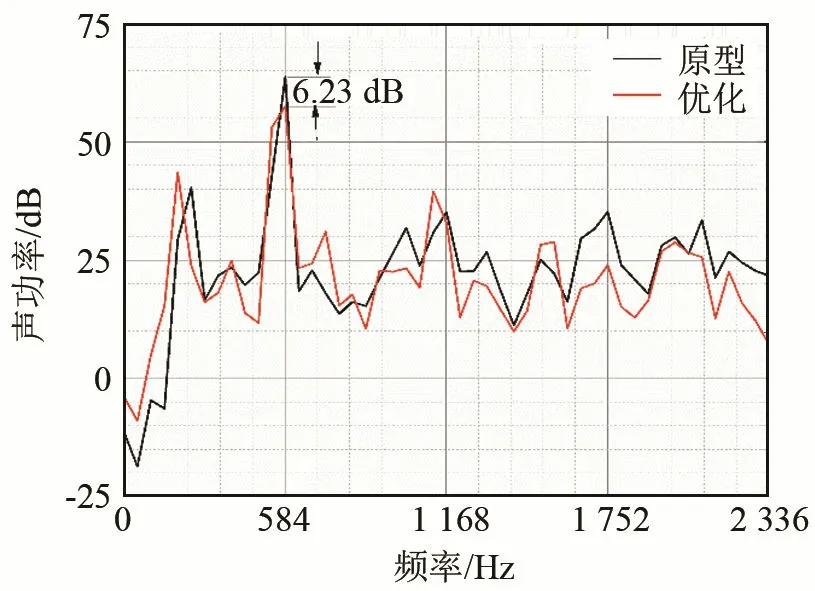
图13 蜗壳结构表面辐射声功率谱Fig.13 The radiated sound power spectrum onthe volute structural surface

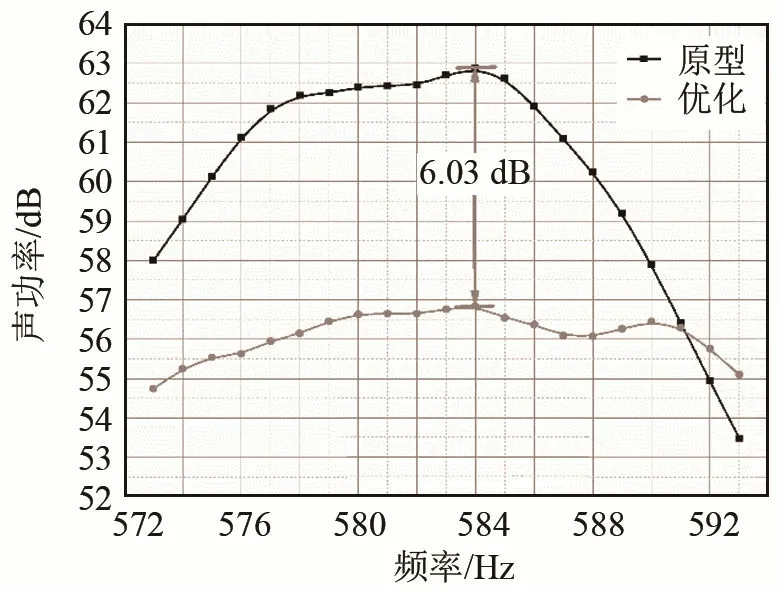
图14 蜗壳结构表面的辐射声功率谱Fig.14 The radiated sound power spectrum on the surface of volute

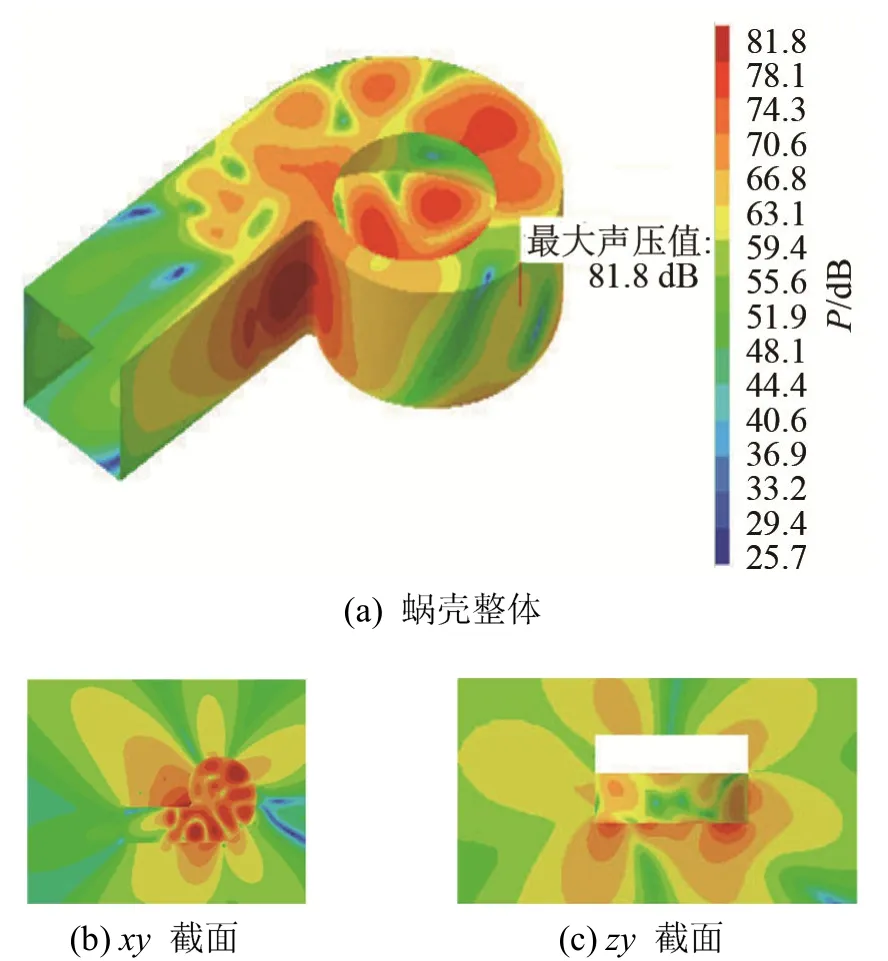
图15 基频下原型风机蜗壳振动声辐射分布Fig.15 The sound radiation distribution of the original volute vibration at the fundamental frequency

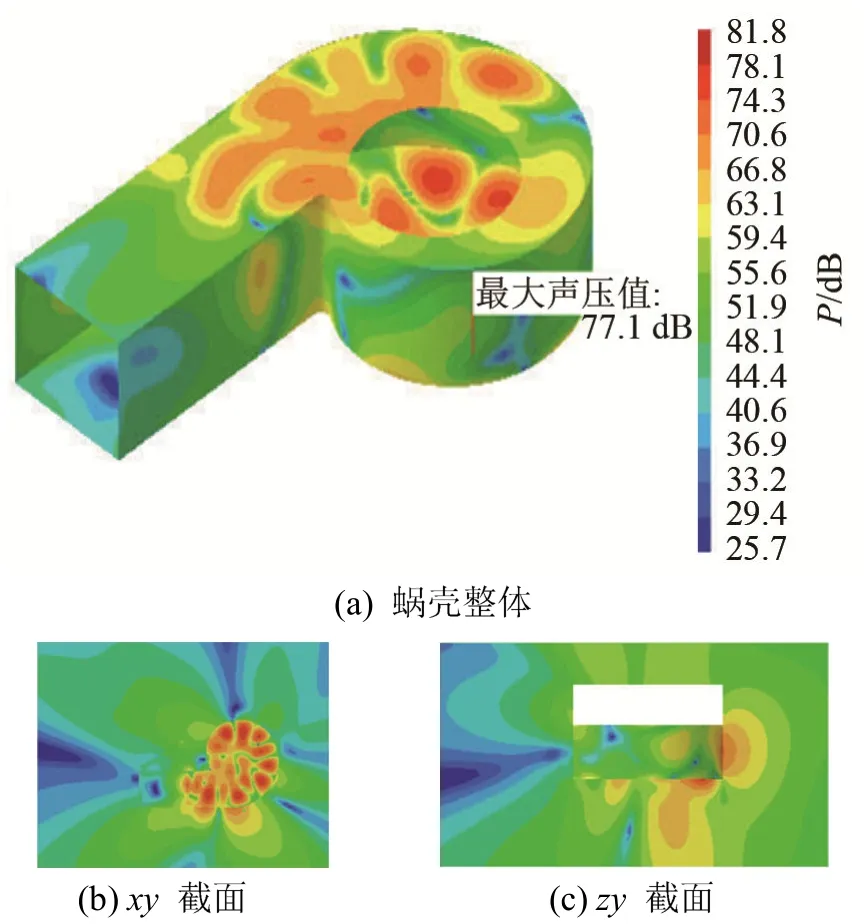
图16 基频下优化的风机蜗壳振动声辐射分布Fig.16 The sound radiation distribution of the optimized volute vibration at the fundamental frequency

3 结 论

(1) 对于大型带有长管道的船用风机系统，研究表明，风机的振动噪声最为突出，为了降低风机振动噪声，本文基于DOE提出了一种考虑振动噪声干涉作用(流体脉动压力单向作用于蜗壳壁面，在计算蜗壳振动在空气中辐射噪声时忽略空气的反作用)的优化设计方法，优化后风机壳体结构表面辐射声功率均有不同程度降低，基频处的噪声降幅最为显著，最大降低了6.23 dB。

(2) 优化后，蜗壳表面的基频(584 Hz)辐射声功率均有较大程度降低，尤其是风机蜗舌附近声辐射功率降幅最为显著，且优化也改善了振动噪声的指向性分布。

本文的优化方法可供此类风机振动噪声控制参考和借鉴应用，获得预期的社会经济价值。