单元重构:凸显知识联系
陈云


摘要:数学知识的教学,教师应引导学生在分析、比较中厘清相关知识之间的区别和联系,理解知识的本质,从数学最本真的意义上去感受知识的整体架构。对苏教版小学数学二年级上册《表内除法(一)》单元内容进行分析,重构为《认识平均分》《认识除法》《用口诀求商》3个课时,并给出相应的教学设计,以凸显知识之间的联系。
关键词:小学数学单元重构知识联系表内除法
数学知识的教学,教师应引导学生在分析、比较中厘清相关知识之间的区别和联系,理解知识的本质,从数学最本真的意义上去感受知识的整体架构。教学苏教版小学数学二年级上册《表内除法(一)》单元,笔者尝试对单元内容进行分析、重构,并给出相应的课时教学设计,以凸显知识之间的联系。
一、单元内容分析
除法作为乘法的逆运算,其意义建构必然要建立在乘法的基础上,且运算操作也必须运用乘法口诀,这决定了除法的学习要和乘法一以贯之。因此,苏教版小学数学教材将《表内除法(一)》安排在二年级上册第四单元,紧接第三单元《表内乘法(一)》。
本单元的内容可以分为三个板块:认识平均分、认识除法和用口诀求商。具体安排如图1所示。
从中可以看到,教材在“认识平均分”板块安排了比较多的内容(4道例题),并且非常注重学生的动手操作(把两种平均分的情形在开放的操作和思考中进行比较),以帮助学生对“平均分”的概念形成具体的表象支撑,从而为除法的认识奠定基础。紧接着,教材通过例5和例6,分别阐释了“平均除”和“包含除”两种情形,旨在帮助学生逐步学会用除法算式表示平均分。这样的安排能分散难点,助力学生学会一定程度的抽象和概括。
但我们同时也会遇到这样一些“疙瘩”:
1.“认识平均分”和“认识除法”两个板块都把“平均除”和“包含除”分到了不同课时进行教学(例2是已知每份数量的平均分,例3是已知份数的平均分;例5是“平均除”,例6是“包含除”)。这样虽然有利于学生逐一突破对不同形式的“除法”的理解,固化某一种分法的过程及结果,但同时也可能会打散知识间的联系,不利于学生统整知识点。
2.在乘法的学习中,教材通过具体情境来帮助学生理解乘法是“求相同加数的和的简便计算”,很好地解释了乘法产生的必要性;而在除法的学习中,教材却把对“平均分的过程就是连续减几个相同减数的问题”的理解放到了“用口诀求商”板块(如图2),这样的编排相对滞后,也显得突兀,没有很好地解释除法算式产生的过程及其必要性。
3.除法是乘法的逆运算,除法的产生和计算都与乘法有着密不可分的关系,但教材并没有在例题中安排相关内容的专题突破,只在练习中安排了除法算式与乘法算式的比较;同时,作为除法的初步认识单元,理解除法的含义和用口诀求商既是本单元教学的重点,又是教学的难点,但教材对这些内容的突破也稍显用力不够。
二、单元内容重构
(一)基于学情,精简课时
二年级学生在经历了一年多的数学学习后,已经有了用“分与合”的方法解决问题的经验,也具备“怎样分就公平”的丰富的生活经验;其思维处于由具体形象思维向抽象逻辑思维发展的过渡阶段,具备一定的迁移能力。因此,学生理解“平均分”的难度并不大,教学应重在让他们经历和比较两种“平均分”的过程,紧接着两种平均分的比较之后,可以出现除法的两种形式,而在“平均除”和“包含除”比较的同时,可以增加除法与乘法的比较,最后可以结合除法与乘法的关系引出“用口诀求商”。这样,虽然增加了除法与乘法比较的相关内容,但新授课时反而可以由5课时精简为3课时。
(二)单元整合,重组内容
由5课时改为3课时,教学内容就要重组:(1)把“用口诀求商”板块中“除法与减法的联系”移到第一课时,引导学生用连减的方法记录平均分的过程;(2)“平均除”和“包含除”对应“已知份数的平均分”和“已知每份数量的平均分”两种分法,可以一边比较两种平均分过程与意义上的异同,一边引入不同形式的两种除法;(3)引入“把一些相同数量合起来”和“把一个总数分成一些相同数量”的分与合的实际问题,通过除法与乘法的比较,使学生感受除法各部分的意义及名称,并通过除法算式与乘法算式各部分之间的联系自主找到“求商”的方法。
(三)把握重点,凸显联系
重组后的3课时,分别对应不同的教学重点。
第一课时《认识平均分》的重点:经历“已知份数”和“已知每份的数量”两种平均分的过程,尝试用减法记录平均分的过程,为除法的教学奠定基础。
第二课时《认识除法》的重点:经历从“平均分”的过程中抽象出除法算式的过程,发现和总结不同的分法列出的除法算式意义上的联系与区别。
第三课时《用口诀求商》的重点:从除法与乘法的比较中发现两者的联系,找到除法算式与乘法算式各部分之间的關系,理解除法运算为什么可以用乘法口诀,并找出一句口诀能解决哪些数学问题。
三、单元教学设计
(一)第一课时《认识平均分》
1.情境引入,发现平均分。
出示问题情境:美工小组正在做纸鹤,王老师把准备好的彩纸平均分给了4位同学,每位同学拿到了3张,你知道王老师准备了多少张彩纸吗?
指名一位学生列式并说一说为什么用乘法计算。
导入:生活中大量存在着像这样要把一些相同数量合成一个总数的问题。
改变问题情境:这时候,又来了两位同学,王老师要重新分配这些彩纸,你觉得要怎么分?
预设:每人分得同样多才是公平的。
小结:每人分得同样多在数学上叫作平均分;生活中也大量存在着像这样要把一个总数分成每份同样多的问题。
[设计意图:从乘法问题引入平均分,让学生初步感知除法与乘法的互逆关系,帮助学生从“合”与“分”的角度去理解乘法与除法的联系。这样的设计贴近学生的“最近发展区”,能有效调动学生学习的内在需求。]
2.联系生活,解读平均分。
提问:你认为怎样就是平均分?
学生根据自己的理解交流,并最终得出:平均分就是每份同样多。
学习活动1:联系生活,说一个平均分的故事。
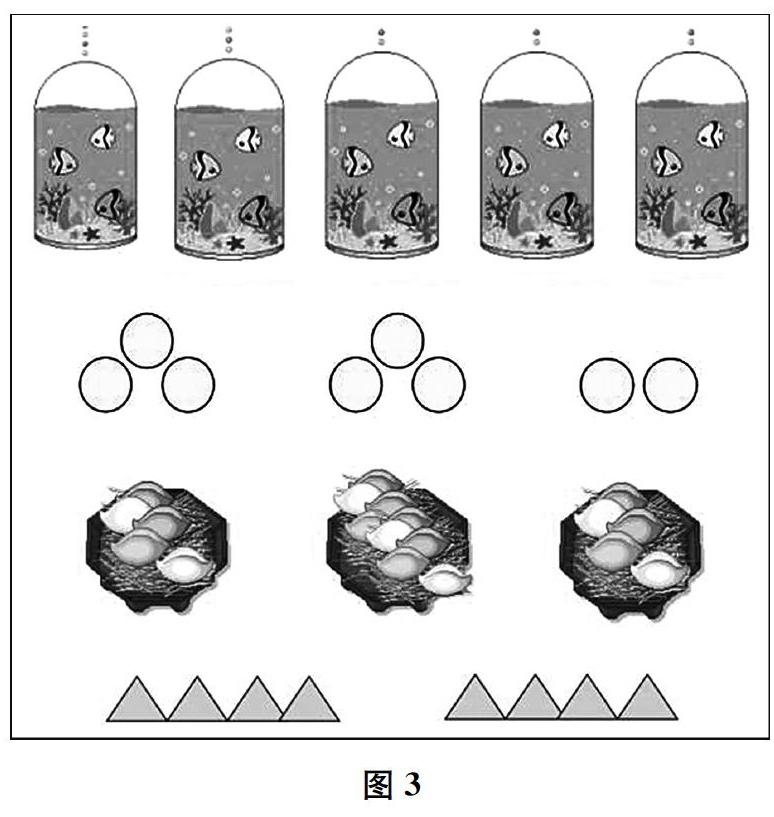
学习活动2:图3中的几种情况是不是平均分?为什么?
[设计意图:引导学生联系已有的生活经验和已学的知识说一说平均分,并结合具体的事例初步建立平均分的表象。]
3.解决问题,经历平均分。
(1)已知每份数量的平均分。
出示问题:这个(不透明)袋子里有一些彩珠,老师想给每位同学两颗,能分给几位同学呢?
先让学生猜测,然后点出:胡乱猜测没有意义,可以实际分一分。
指名一位学生上台操作分的过程:先拿出两颗递给第一位同学。
提示:现在老师袋子中的彩珠发生了什么变化?(少了两颗)怎么记录这个过程?
引导用符号(如“?”)代替袋子中未知的数量,拿走两颗就是减去2。
学生继续操作并记录,最终得到:?-2-2-2=0。
引导小结:①总数是6;②6里面有3个2;③已知每份数量的平均分的过程可以表示成连减的算式。
(2)已知份数的平均分。
出示问题:老师这里还有一个袋子,里面也有一些彩珠,我想把它们平均分给3位同学,每位同学能分到几颗彩珠?
组织学生交流分法,并请一位学生上台操作。
结合学生操作,逐级追问:为什么不像刚才那样,把每人应得到的彩珠直接分给他?当每人分得一颗彩珠时,袋子中的彩珠总数发生了怎样的变化?
引导交流、总结:因为不知道每人能分到几颗,所以要逐次分;为了保证每人最终分到的數量同样多,可以一次给每人分一颗,如果还有剩余,再接着分。
再请一位学生上台分一分,其他学生记录分的过程:?-3-3-3-3=0。
引导小结:①总数是12;②12平均分成3份,每份是4;③已知份数的平均分的过程也可以表示成连减的算式。
(3)“动手做”。
提问:用18个相同的小正方形拼成不同的长方形,你想怎么分?
引导分两种情况思考:①先确定要分的行数,再实际分一分,看每行能分几个;②先确定每行的数量,再试一试可以分成几行。
[设计意图:在开放的活动中,学生通过对比感受到,虽然两种分法分的过程有区别,但其本质还是有内在联系的。用减法记录分的过程,建立起减法和除法之间的联系,为除法的产生做铺垫。“动手做”环节,用18个小正方形拼长方形,是对两种平均分过程的再比较,同时也是对除法与乘法联系的再感知。]
(二)第二课时《认识除法》
1.结合平均分,引出除法。
出示问题:24只气球,每4只扎一束,可以扎成几束?
引导列出算式(24-4-4-4-4-4-4=0),得出:24里面有6个4,所以可以扎成6束。
追问:这是一个什么问题?减法表示什么?如果这里有48只气球呢?96只气球呢?
引导发现:随着数字增大,用减法来解决太麻烦了。
引发思考:在前面的学习中,我们知道,一些相同加数相加时,为了简便,可以列乘法算式,那么想想看,这里连续减一个相同的减数,会不会有什么简便的方法呢?
引入除法:像这样平均分的问题在数学上可以用除法来计算,把24只气球平均分,每份4只,就可以写成24÷4;刚刚我们已经知道可以分给6个人,所以就等于6。
介绍除号的写法和读法,以及表示的意义(平均分)。
[设计意图:引入较大数平均分的问题,让学生感受用连减的方法来解决很麻烦;再结合乘法是“求相同加数的和的简便计算”这一已有认知,迁移猜想连续减一个相同减数,一定也有相应的简便计算,顺理成章地引入除法。]
2.认识除法,解读算式的意义。
结合分气球情境,指名学生说一说“24÷4=6”中每个数字表示的含义。
提问:回顾上节课“分彩珠”的过程,6颗彩珠,每人分两颗,可以分给几位同学?这个问题你能用除法算式来表示吗?并说一说这道算式表示的意义。
置换问题情境:24只气球,平均扎成4束,每束有几只?这个问题可以列成除法算式吗?为什么?请你列出算式,并说一说算式的每一部分分别表示什么。
引导用同样的方法解决上节课其他“分彩珠”问题。
[设计意图:通过相同情境中的两种不同分法,引导学生了解除号和除法算式所表达的意义,并用除法解决上节课中的平均分问题,进一步感受用除法解决平均分问题的便捷。]
3.比较除法,认识各部分的名称。
同屏出示两道除法问题和算式,引导观察比较:这两个问题有什么相同点和不同点?
引导小组交流、全班汇报。相同点:都是表示平均分的问题,所以都是用除法解决;都是已知总数(教师结合学生的汇报介绍:这个总数在除法中就是被除数,也就是这个总数被平均分了)。不同点:一题是已知每份的数量,另一题是已知份数(教师结合学生汇报介绍:这个已知的量不管是每份的数量还是份数,在除法中就是那个被连续减的减数,叫作除数);最后求出来的结果表示的意义也不同(教师介绍:这个最终结果的意义不同,但都叫作商)。
请学生独立完成课本“反馈习题”,并指出被除数、除数和商分别在哪里,表示什么意思。
提问:除法中这个总数叫“被除数”,减法中的总数叫“被减数”,都有一个“被”字,你能说说你是怎么理解的吗?
引导发现:“被除数”和“被减数”都是总数,都是被分的对象;减法可能不是平均分,除法一定要是平均分;减法算出的是其中一个部分的数量,除法算出的是所有部分相同的数量或有几个相同的部分。
[设计意图:通过对“平均除”和“包含除”两种除法的对比,引导学生发现其本质意义是相同的,进一步强化对除法的理解。通过“被除数”“被减数”两个名称上的相似,引导学生找到除法与减法的联系与区别,打通知识间的“隐蔽通道”。]
(三)第三课时《用口诀求商》
1.联系实际,感受除法与乘法的互逆关系。
出示问题情境:学校给每个班分发了一些必读书籍,王老师把这些书整整齐齐地摆放在书桌上,(1)每堆放4本,5堆一共多少本?(2)一共有20本,每堆放4本,可以放几堆?(3)一共有20本,平均分成5堆,每堆可以放几本?
指名学生列式并说一说为什么用乘法或除法计算。
提问:观察这3个问题,你能说说什么时候用乘法计算,什么时候用除法计算吗?
引导发现:问題(1)求总数,5个4相加就能得到总数,可以用乘法计算;问题(2)和问题(3)都是已知总数,把这个总数连续减,也就是平均分,可以用除法计算。
[设计意图:通过同一情境下的除法与乘法问题的比较,感受乘法是求总数,除法是已知总数求份数或每份数量,除法与乘法之间存在互逆关系,为用乘法口诀解决除法问题做铺垫。]
2.用口诀计算。
提问:乘法你能用乘法口诀计算,那除法呢?不看图你会计算吗?你是怎么想的?
预设:(1)从乘法中去找,乘法的积是被除数,一个乘数是除数,另一个乘数就是商;(2)20÷4,其实也就是想4个几是20,同样可以用4的乘法口诀计算;(3)实际分一分,就知道商是几;(4)用20连续减4,看能减几个4。
引导比较:这几种算法有什么共同点?哪种方法更简便?
提问:通过这几道题的计算,你发现了什么?
引导发现:“四五二十”这句口诀可以用于计算4×5、5×4、20÷5、20÷4四道算式。
反馈练习:(1)看算式想口诀;(2)看口诀写四道算式。
[设计意图:引导学生先用乘法口诀解决乘法问题,再思考怎么计算除法算式。在对多种计算方法的比较中发现其实质都是求4个几是20,归结到乘法口诀可以解决的问题上来,并通过反馈练习巩固一句口诀对应的乘法和除法算式。]
3.自主编题。
出示图4,提问:看图,你能写出一道乘法算式和两道除法算式吗?
指名学生列式。
引发思考:你要运用哪些数学信息,提出怎样的问题,才能列出乘法算式?要列出除法算式呢?你又是怎样计算这些乘法、除法算式的?
[设计意图:从看问题列算式,到看图提出用乘法和除法来解决的问题,学生的思维要更加理性——要提出用乘法解决的问题,就不能在信息中涉及总数,而要把求总数放在问题里;要提出用除法解决的问题,就要先表明总数是多少,再平均分,由此可以进一步巩固除法和平均分模型。]

