基于随机森林与变邻域下降的车辆合乘求解
郭羽含,胡德甲
辽宁工程技术大学 软件学院,辽宁 葫芦岛 125105
1 引言
随着经济快速发展,人们生活水平日益提高,城市中私家车数量大量增加。随之带来的环境污染、交通堵塞以及私家车花费问题日渐严重[1],引领网约车、拼车系统等车辆合乘模式的逐渐兴起[2]。生活中上下班拼车、回家拼车以及旅游拼车越来越普遍。车辆合乘是指有车人员和无车人员之间或有车人员与有车人员之间的一种合作形式,费用由合乘组成员共同分担。随着私家车数量的持续上升,无车人越来越少,长期车辆合乘应运而生。长期车辆合乘主要是根据大中型城市上班族上下班时间接近、上班地点集中以及居住较分散的现状以及解决上下班时间交通压力过大的问题提出的上下班模式,是指具有合乘意愿且乘车路线相近的人们分成同一小组乘坐同一辆车,合乘费用分摊的模式。这种合乘关系是长期合作的关系,可以降低临时或短期合乘的安全隐患,并减少临时或短期合乘进行多次匹配所带来的资源浪费。
合乘问题的研究对于物流优化以及城市交通规划具有重大意义。国内外学者对合乘路径规划、车辆调度以及模型算法等领域研究较多。例如Dakroub等[3]针对小规模车辆合乘问题提出一种改进的遗传算法高效求解合乘方案;Filcek 等[4]研究考虑司机与乘客之间不同标准多目标合乘优化问题,通过加权函数聚合所有目标,应用贪婪算法为全部合乘组生成最佳行驶路线;宋超超等[5]提出基于吸引粒子群算法解决多车辆合乘问题;邵增珍等[6]提出的两阶段聚类启发式优化算法解决多车辆合乘问题,第一阶段通过提出匹配度概念将多车辆合乘问题转化为单车辆匹配问题,第二阶段基于“先验聚类”插入思想提高算法效率。对客户属性以及满意度研究较少,现在比较热门的出行安全事件引起人们重视[2]。何胜学等[7]通过建立考虑性别偏好影响的通勤合乘匹配模型,利用同性同组占优原则进行合乘匹配,分别处理了同性合乘、异性合乘、特别组合三种性别合乘模型,一定程度上提升了用户满意度但仅仅考虑了性别单个属性。过去的研究主要是针对小规模车辆合乘问题的研究[8-10],He 等[11]通过建立考虑性别偏好影响的通勤合乘匹配模型,利用同性同组占优原则进行合乘匹配,分别建立了同性合乘、异性合乘、特别组合三种性别合乘模型,一定程度上提高了安全系数和提升了用户满意度,但该方法仅考虑了合乘人员性别单个属性,具有一定的局限性。卢佐安等[12]通过考虑客户满意度的因素,建立客户满意度最大和运输成本最小双目标函数优化模型,较好的平衡了客户满意度和运输成本,但过多考虑时间属性,并没有对其他因素进行较为全面的考虑。进一步,张玉青[13]提出通过KANO模型对用户需求进行绩效指标分类,根据分类结果,将不同用户需求进行区别处理,该方法通过了解不同层次用户需求,识别影响客户满意的至关重要的因素,利用KANO模型对属性进行分类,以车辆合乘用户进行检验,得到了较高的客户满意度。王银虎[14]建立出租车服务水平最高为优化目标,将合乘出租车动态调度拆解成一系列静态时间点保证出租车司机在一定时间内使得资源以及收入达到最优,进而提出“上下”双层算法进行优化,上层算法进行调参,下层算法基于上层算法得到参数对模型进行求解。可见,在合乘问题中,为了提高乘客在某一方面的满意度,侧重考虑某一乘客属性以及乘客满意度因素,得到的结果均有所提高。对于大规模车辆合乘问题求解不适用,存在求解时间长,得不到较优解以及用户属性考虑片面达不到用户满意的问题。
针对长期车辆合乘问题(Long-Term Car Pooling Problem,LTCPP),为了最大化用户对合乘结果的满意度,需要考虑多个优化目标。本文首先构建了带有车容量和时间窗约束的多目标优化模型,在将其转化单目标优化时,权重因子的选择对优化结果起着至关重要的作用。人为设定权重因子主观性太强,达不到绝大多数用户的满意。因此,本文使用机器学习中决策树集成算法Bagging模型中的随机森林算法对历史合乘数据及用户满意度进行分析,并得到各个指标对用户满意度的重要性影响,作为对应优化目标的权重。然后,提出了一种求解LTCPP的变邻域下降(Variable Neighborhood Descent,VND)算法。实验结果表明,结合随机森林算法和VND算法能够高效地为LTCPP提供高质量的解决方案。
2 问题定义和数学模型
对LTCPP问题进行了简单定义,介绍了数学模型。
2.1 问题定义
LTCPP就是指假设每个参与者都拥有一辆私家车,并且他们的目的地相同或相近,出行时间接近。合乘前概况图如图1 所示。每位参与者都有各自的最早出发时间、期望出发时间、最晚到达时间、期望到达时间、年龄、性别、最长驾驶时间以及最大载客量。每位参与者也有独乘和合乘两种方式,在满足每位参与者时间窗和车容量的前提下,将所有用户分成若干个合乘组(一个合乘组形成后如图2 所示),每个小组中的合乘者按照轮流驾驶的原则利用算法最小化所有小组出行花费的总和。

图1 合乘前用户出行示意图

图2 合乘后用户出行示意图
2.2 数学模型
2.2.1常量定义
C:参与合乘的用户集合;
0:目的地;
E:边集合,
K:合乘组集合;
Xi:用户i性别,用0、1表示;
Ai:用户i年龄;
Ti:用户i所能接受的最长驾驶时间;
Ri:用户i的车容量;
edti:用户i的最早出发时间;
qdti:用户i期望出发时间;
lati:用户i最晚到达时间;
qati:用户i期望到达时间;
(xi,xj):用户i的地理坐标;
dij:用户i、j间的距离;
tij:用户i前往用户j所需的驾驶时间;
ρ:惩罚系数。
2.2.2变量定义
yik变量表示用户i是否在合乘组k中,0表示用户i不在合乘组k中,1表示在。
φi变量表示用户i出行方式,0 表示用户i与其他用户合乘,1表示用户i单独出行。
ti变量表示用户i当司机时的实际驾驶时间。
Agek变量表示合乘组k内成员年龄Ai的平均值。
Xbk变量表示合乘组k的性别惩罚值,同性惩罚值为0,否则为1。
2.2.3目标函数及约束
LTCPP 以最小化所有用户出行花费最小为优化目标,即最小化所有合乘组出行花费之和。设k为一个合乘组用户的集合,用户h(h∈k)为某日合乘组k的司机,用户h在满足|k|≤Rh以及用户i(i∈k)的时间窗的约束下从h出发依次走遍用户i(i∈k⋀i≠h)最终到达目的地0即为可行路径,从所有可行路径中选择最优路径。将所有用户h(h∈k)的最优路径长度累加后除以合乘组k的成员数量|k|,即为合乘组k的平均每日出行花费。
此外,为了增加用户满意度,还需要最小化用户实际出发/到达时间与期望的实际出发/到达时间的差距、合乘所产生的额外驾驶时间、用户年龄与组内平均年龄差值、用户性别与组内平均性别值差值以及单独出行用户数。将多个优化目标的加权和作为目标函数,并通过引入惩罚值来减少单独出行的用户数量。目标函数如公式(1)所示,其中,α、β、γ、δ、ε分别为所有合乘组平均每天行驶里程之和、所有用户实际出发到达时间与期望出发到达时间差值之和、所有用户担任司机时实际驾驶时间与单独出行时间差值之和、所有用户年龄与组内平均年龄差值之和、所有用户性别与组内平均性别值差值之和的权重因子。

s.t.

约束(2)确保满足车容量约束,即合乘小组人数小于等于用户车容量;约束(3)确保用户h在合乘小组k中做司机的驾驶时间不超过其最大驾驶时间;约束(4)和(5)确保满足用户出发时间约束,即用户h在合乘小组k中做司机时,确保用户i的出发时间大于等于其最早出发时间;约束(6)和(7)确保满足用户到达时间约束,即用户h在合乘小组k中做司机时,确保用户i的到达时间小于等于其最晚到达时间;约束(8)~(10)确保若用户i(或j)在司机h的行驶路径中,则用户i(或j)必须在合乘组k中;约束(11)确保用户的出行方式一致性;约束(12)~(14)为二进制约束;约束(15)~(17)为非负约束。
3 随机森林与变邻域下降
介绍了使用随机森林算法计算特征重要性的方法,以及求解LTCPP的VND算法。
3.1 随机森林算法
LTCPP问题属于多目标优化问题,在将其转化单目标优化时,权重因子的选择对优化结果起着至关重要的作用。但现今权重因子的选择大多凭经验人为设定,主观性太强,袁丽莎等[15]提出了一种结合深度神经网络和随机森林的手掌静脉分类新方法,自动提取手掌静脉特征并进行分类识别,避免了人工选择特征提取算法的局限性。为了避免人为设定权重因子的主观性,本文通过随机森林算法根据历史合乘组信息以及用户满意度,计算出各个特征对用户满意度的重要性影响,即采用特征重要性作为对应优化目标的权重因子。
3.1.1决策树的构造
特征和类别:
特征1(difD) 用户与合乘组重心的距离;
特征2(difI) 用户实际出发/到达时间与期望时间的时间差;
特征3(difT) 用户合乘产生的额外驾驶时间;
特征4(difA) 用户与合乘组平均年龄的差值;
特征5(sexD) 用户所在合乘组的性别分布。
这5个特征对应于目标函数中的5个优化目标。
类别用户对合乘组的满意度评分,取值为1~10,共10个类别。
收集到历史合乘组信息后,需要对每个用户对应的特征值进行计算,得到的特征值及类别将用于后续决策树模型的训练,如表1为样本集示例。
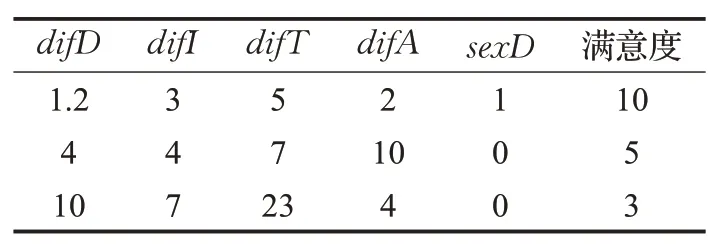
表1 样本示例
特征值计算过程如下所示。
用(xk,yk)表示合乘组k的重心,则:
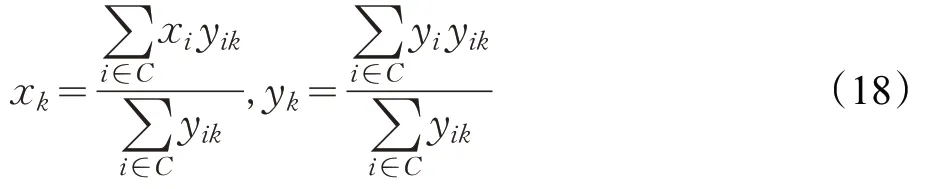
用户i到合乘组k重心的距离difDi:
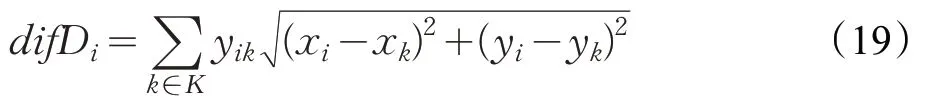
用户i实际出发时间与期望出发时间差difDi:

用户i实际到达时间与期望到达时间差difFi

用户i实际的与理想的出发到达时间差difIi

用户i参与合乘产生的额外驾驶时间:

用Agek表示合乘组k组内平均年龄,则:

用户i与合乘组k平均年龄的差值difAi:
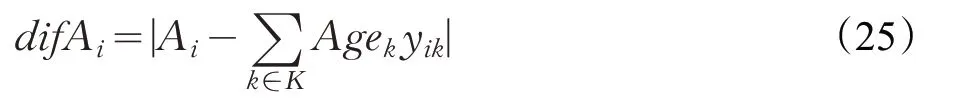
用户i所在合乘组的性别累加sexSi:

用户i所在合乘组的成员数量MNi:

用户i所在合乘组的性别分布sexDi,组内成员全为同性sexDi取值为1,否则为0:

构造决策树,就需要根据样本数据集的数据特征对数据集进行划分,直到针对所有特征都划分过,或划分的数据子集的所有数据的类别标签相同。划分数据集的原则就是将无序的数据变得更加有序,也就是使数据集的熵值变得更小,而节点特征的选取都可以使数据集的熵值减小,从根节点到子节点选取的依据全都是选择使熵值变化最大的特征,即选取信息增益最大的特征。
构造决策树过程如下。
(1)收集数据:收集历史合乘组信息以及用户的满意度评分。
(2)数据预处理:根据合乘组信息计算对应的特征值,得到样本数据集。决策树构造算法只适用于标称型数据,因此,还需要对连续型变量进行离散化处理。


(3)构造模型:构造决策树模型。
(4)训练和测试模型:将数据分成训练集和测试集对决策树模型进行训练和测试。
(5)使用模型:将完整的决策树算法投入接下来的随机森林。
3.1.2随机森林
随机森林是包含多个决策树的模型,其输出的类别是由单个树输出的类别的众数而定,因此它要比单个决策树模型具有更高的分类准确性。此外,随机森林模型具有能够输出特征重要性的特点,本文根据这一特点来确定各优化目标的权重,计算过程如下:
(1)从原始历史合乘数据集中使用Bootstraping 方法随机抽取n个训练样本,共进行k轮抽取,得到k个训练集。k个训练集之间相互独立,数据点可以有重复。
(2)对于k个训练集分别训练出k个决策树模型。
(3)对于单个决策树模型,每次划分是根据信息增益选择最好的特征进行划分,直到该节点的所有训练样本数据都属于同一类。
(4)将生成的多棵决策树组成随机森林,按多棵树分类器投票决定最终分类结果。
(5)计算特征重要性。
特征重要性即特征对分类结果的影响比重。特征重要性通常用Gini 指数或者袋外数据错误率作为评价指标来衡量。
本文以Gini指数作为衡量标准来计算特征重要性,下面是具体计算过程:
Gini指数又称基尼不纯度,表示样本集合中一个随机选中的样本在子集中被分错的概率。Gini 指数为这个样本被选中的概率乘以它被分错的概率。当一个节点中所有样本都属于同一个类别时,Gini指数为零。节点m的基尼指数为:

式中,K为类别个数,pmk表示节点m中随机选中一个样本属于k类别的概率。
特征j在节点i的重要性为选择特征j对节点m进行一次划分后Gini 指数差值,划分后产生新的节点l、r,那么:
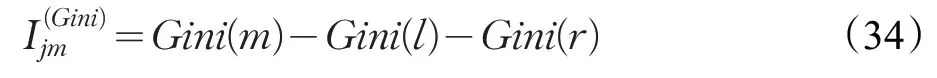
集合M表示决策树i中特征j出现的节点集合,那么特征j在这棵树上的重要性:

假设随机森林中有n棵树,那么特征j的全局重要性为通过特征j在单颗树中的重要性的累加:

最后,将所有求得的特征重要性做归一化处理:

3.2 变邻域下降算法
变邻域下降(VND)算法是顺序地在多个邻域内搜索的启发式算法,它的成功在于不同的邻域结构通常具有不同的局部最小值,因此VND 比一般的局部搜索算法更有可能搜索到全局最优解。VND以随机或结构化的初始解开始,然后在当前解的当前邻域内进行探索,如果找到更好的解,则以新的解决方案作为当前解,返回第一个邻域重复搜索过程,否则进入下一个邻域探索。当探索完所有邻域,无法找到比当前解更好的解决方案时,算法停止。算法1展示了VND的伪代码。
算法1 变邻域下降算法(VND)
1.构造初始解s
2.定义邻域结构{N1,N2,…,Nkmax}
3.Fortokmaxby 1
(1)找到s的最佳邻居解
(2)If//当前解获得改进
(3)End If
4.End For
5.Returns
基于该算法框架,本文将其用于求解LTCPP,3.2.1小节介绍了初始解的构造方法,3.2.2小节介绍了4种邻域结构,3.3.3 小节介绍了LTCPP 完整解决方案的求解方法。
3.2.1初始解的构造
相比于随机生成的初始解,一个设计良好的初始解可以缩短搜索到最优解的时间。因此,本文提出如下方法来产生初始解决方案。
该方法的主要思路是按照用户的地理分布,每次从用户集合中选择相距最远的两个用户分别建立合乘小组,然后将与他们临近的用户分配到各自所在的合乘小组中,直至所有用户都被分配到合乘组为止。初始解构造方法的伪代码如算法2所示。
算法2 初始解构造方法
1.对所有用户按照其坐标x+y的值进行排序,排序后的用户存储在集合U中
2.pools←{} //合乘小组集合
3.WhileU.size()!=0 do
(1)IfU.size()==1
U.remove(d1);
pools.add(pool);
break;
(2)End If
(3)选择U中排列在第一位的用户d1←U.get(0)建立一个合乘小组pool1,并将其从集合U中移除
(4)使Cpool1←Rd1-1 表示d1所在合乘组小组还可容纳用户数量
(5)While(Cpool1!=0)&&(U.size()!=0)do
从集合U选择离d1最近的用户i加入pool1,并将其从U中移除;
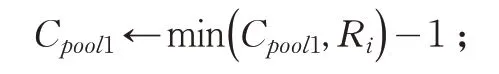
(6)End While
(7)pools.add(pool1)
(8)IfU.size()==0
break
(9)End If
(10)选择U中排列最后一位的用户d2←U.get(U.size()-1)建立一个合乘小组pool2,并将其从集合U中移除
(11)使Cpool2←Rd2-1 表示d2所在合乘组小组还可容纳用户数量
(12)While(Cpool2!=0)&&(U.size()!=0) do
从集合U选择离d2最近的用户j加入pool2,并将其从U中移除;
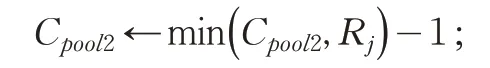
(13)End While
(14)pools.add(pool2)
4.End While
5.Returnpools
3.2.2邻域设计
邻域N(s)可以定义为邻居解s′是通过对当前解s应用某种变化得的},本文设计了4种邻域结构,分别与分割、2-opt、移动、合并操作相关联。这4 种邻域会被顺序地进行搜索。
(1)分割邻域N1
分割邻域N1(s)是通过对当前解s应用分割操作得到的解的集合。对当前解s中所有合乘组(合乘组成员数量为1 的除外)应用一次分割操作来获得当前解s的一个邻居解。分割操作即将一个合乘组分割为两个新的合乘组,分割时需要考虑所有的可能情况。例如合乘组成员数量为4,则有1、3和2、2两种分割方式,数字表示分割后新的合乘组成员数量。新的合乘组成员组成也是通过枚举所有可能的组合找到能使得目标函数降低的分割方式。一旦合乘组找到使得目标函数降低的分割方式,则确认该分割操作,换下一个合乘组应用分割操作。如图3展示了1、3分割的一个例子。
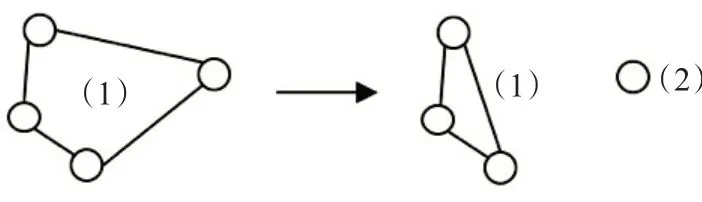
图3 分割操作
(2)2-opt邻域N2
2-opt邻域N2(s)是通过对当前解s应用两两交换操作得到的解的集合。通过将当前解s中的所有合乘组与其他合乘组进行成员两两交换来获得当前解s的邻居解,该交换操作尝试合乘组中的所有用户,一旦交换后使得目标函数降低,则确认该交换,换下一个合乘组应用交换操作。在图4 中,通过将合乘小组(1)、(2)中的成员进行互换得到新的合乘小组。新的合乘组用户与合乘组重心的距离更近。

图4 2-opt操作
(3)移动邻域N3
移动邻域N3(s)是通过对当前解s应用移动操作得到的解的集合。通过将当前解s中所有的合乘小组的成员移动到其他的合乘小组来获得当前解s的邻居解。移动后的合乘小组仍需满足车容量约束。尝试移动合乘组中的每一个用户至其他合乘组,直到移动后使得目标函数降低,则确认该移动,换下一个合乘组进行移动。在图5 中,合乘小组(2)中距离其他成员较远的成员被移动到合乘组(1)中。
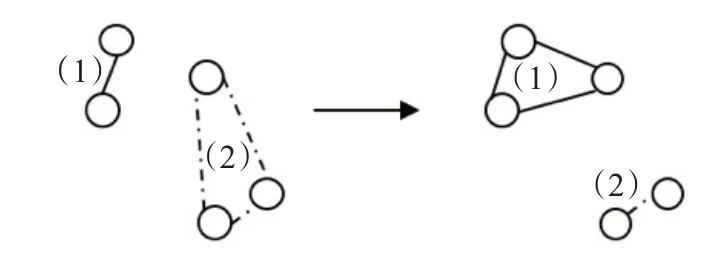
图5 移动操作
(4)合并邻域N4
合并邻域N4(s)是通过对当前解s应用合并操作得到的解的集合。通过将当前解s中组员数量未达到车容量的合乘小组进行两两合并来获得当前解s的邻居解。合并后的合乘小组需满足车容量约束。尝试将合乘组与其他每一个未达到车容量的合乘组进行合并,一旦合并后使得目标函数降低,则确认该合并操作,换下一个合乘组进行合并。在图6中,相距很近的合乘小组(1)、(2)被合并为一个合乘小组。

图6 合并操作
3.2.3完整解的求解方法
将LTCPP 的解表示为两层结构。第一层表示用户的分组情况,第二层表示用户担任司机时的具体路由信息。该信息与每个用户i∈C相关联,具体包括:用户i担任司机的行驶路径Pi、接载合乘组成员的时间表Ci、行驶里程数disi、行驶时间timi、到达目的地时间arvi以及用户是与其他用户合乘还是单独出行φi。解的结构如图7所示。

图7 一个解决方案的表述
通过VND 算法可以得到用户的分组情况,即得到了解的第一层信息。因此,接下来介绍如何根据分组信息得到LTCPP完整解决方案。
该问题是赋权哈密顿回路最小化问题,即给定n个点以及点与点间的距离,找到一条回路由指定的起点前往指定的终点,经过图中所有点且只经过一次,要求整个回路的总距离最短。这一问题可以通过枚举法进行求解,其计算量为(n-2)!。这种精确算法对于大多数问题是不可行的,但在本文中,一个合乘小组的成员数量通常不大于5,因此该问题规模非常小,完全可以使用枚举法来获得最优的哈密顿回路。图8(a)给出了一个计算实例,其中U1、U2、U3、U4 为同一合乘小组,通过对除起点和终点外的其他点的顺序进行全排列,可以得到U1 作为司机时所有可能的行驶路径如图8(b)所示。路径1的距离:(6+2+3.5+21)=32.2,类似地,可以得到路径2、3、4、5、6 的距离分别为:35.5、34、37.5、34.5、35。因此路径1 为U1 的最佳行驶距离,即R1={U1,U2,U3,U4},其他第二层解信息可以基于该变量得到。

图8 哈密顿回路示例
在计算最短哈密顿回路时,进行时间窗检查,对于不满足时间窗约束的合乘组,通过将其不断地划分为更小的合乘组直到所有的合乘组都满足时间窗约束。
4 实验与分析
本章将仿真实验,以验证算法的有效性及效率,并对实验结果进行分析。
4.1 实验环境
本文所提出的算法均由Java 语言实现。实验所用的计算机配置为2.7 GHz Intel Core i5CPU,8 GB 内存,操作系统为OS High Sierra 10.13.6。
4.2 实验数据
由于LTCPP 没有基准数据集,因此,本文采用如下方法生成测试实例。以坐标原点(0,0)表示目的地,用户地理坐标x、y取值范围为[−60,60],用户以3种分布方式:集中(C)、随机(R)、混合(RC)分布在原点周围,用户数量分别设置为 100、200、400、600、800、1 000、1 500、2 000。所有测试实例均由程序生成。
4.3 实验结果
用户数量(Size)、训练集比例(Training set)以及测试集比例(Test set)对随机森林得分(Score)的影响如表2所示,由于随机森林随机提取测试集,即使相同的用户数据、训练集比例以及测试集比例也会得到不同的实验结果,每次相同数据进行50 次实验取平均值得到表中数据,从表中数据可知,训练集比例以及测试集比例对所构造的森林得分无较大影响,训练集比例取值为0.6时,森林得分较好;测试集比例不能过小,以免影响测试森林得分,无法公正评估森林准确性。随着用户数量的增加,得到的森林越加准确,到最后35 000个数据时,森林得分趋于稳定,所以本文中取35 000 个用户历史数据,训练集比例为0.6,测试集比例为0.4进行实验。

表2 用户数量、训练集测试集结果分析表
选取35 000个用户历史数据,测试集比例为0.6,训练集比例为0.4,进行100 次实验,因为随机森林测试集选取的随机性,每次得到的各项权重因子并不完全相同,取森林得分测试结果高于0.975的实验,进行平均处理得到各项权重因子。部分实验结果如表3所示。
通过随机森林模型对历史分组数据进行学习,得到各个特征对用户满意度的影响权重。其中,特征difD的重要性为0.71,特征difI的重要性为0.14,特征difT的重要性为0.03,特征difA的重要性为0.04,特征sexD的重要性为0.07。特征重要性将作为下一阶段采用VND 算法求解LTCPP 时目标函数中各优化目标的权重,即α=0.71,β=0.14,γ=0.03,δ=0.04,ε=0.07。将与文献[16]中的聚类蚁群算法(Clustering Ant Colony algorithm,CAC)进行对比,该文献中的各优化目标的权重均由人为设定。实验结果如表4所示,其中,Size表示用户数量,Rcar表示合乘后平均每天的出行车辆减少率,该值可以计算为:Rdis表示为合乘后平均每天用户行驶里程减少率,Din表示平均用户与合乘组的距离,Ain表示平均用户与合乘组平均年龄的差值,Rs表示合乘组全为同性成员的比率,Tg表示平均每位用户每天的实际出发到达时间与理想的时间差,Te表示合乘后平均每位用户每天的额外驾驶时间,Tc表示算法求解时间,表示CAC算法在5个节点集群上计算时间,表示CAC算法在10个节点集群上计算时间。
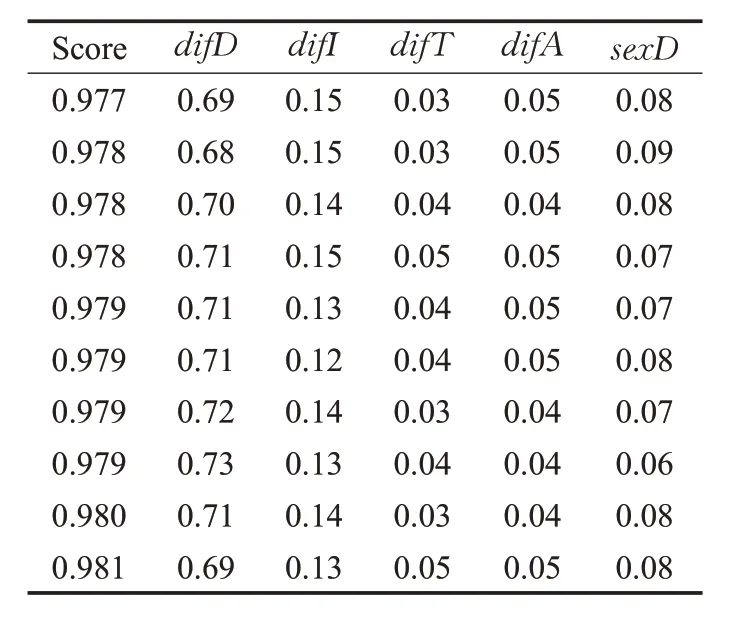
表3 权重因子实验结果

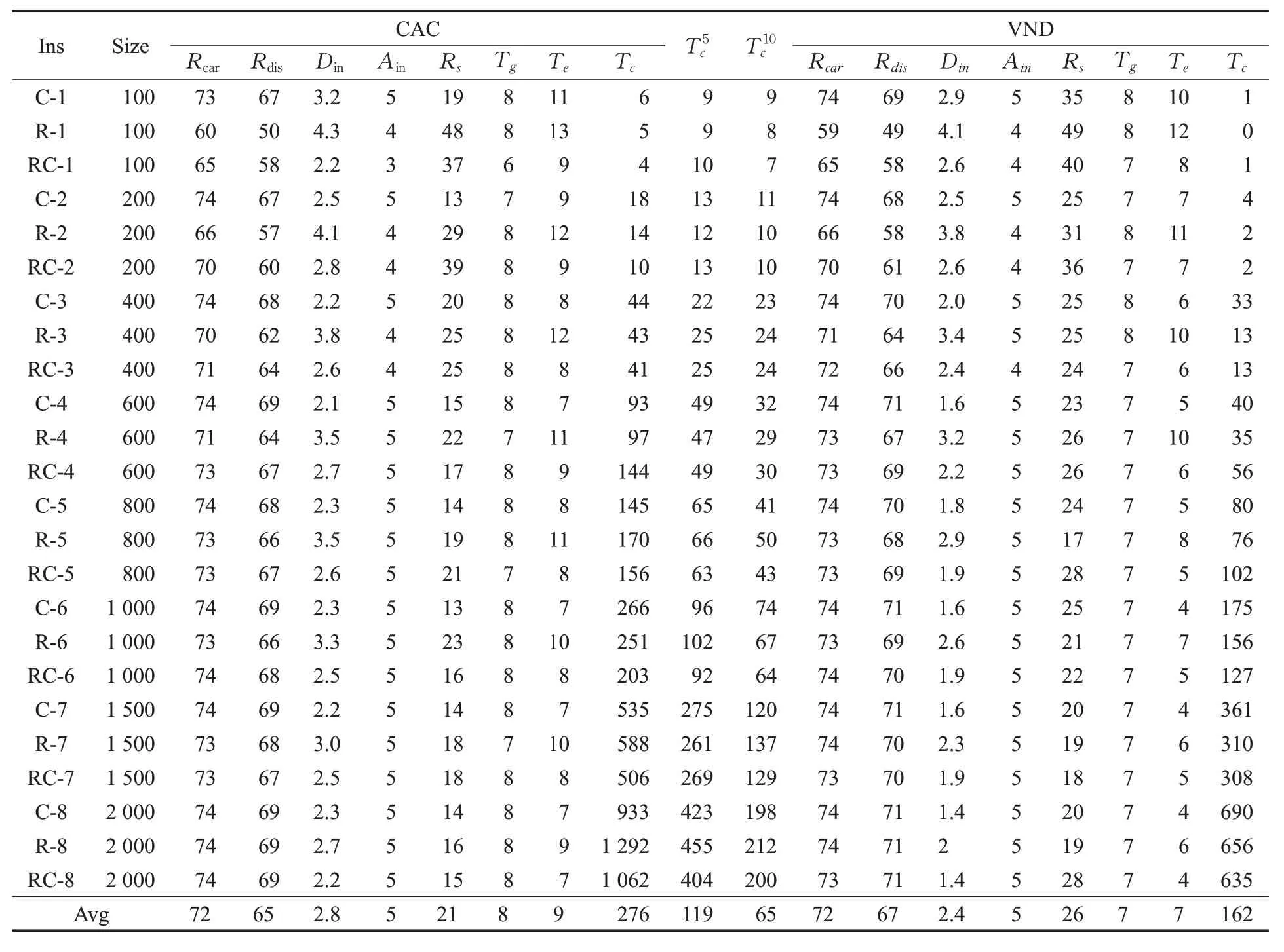
表4 实验结果
4.4 结果分析
4.4.1有效性分析
为了验证通过VND 算法得到的合乘方案的有效性,从指标Rcar、Rdis、Din、Ain、Rs、Tg、Te进行验证。从表1可以看出,用户参与合乘后平均每天可以减少Rcar=72%的出行车辆,每天总行驶里程减少Rdis=67%。用户离合乘组重心的平均距离Din=2.4 km,这说明一个合乘组中的成员通常分布在以2.4 km 为半径的圆形范围内。用户与合乘组内平均年龄的差值约为Ain=5岁。合乘组成员性别均相同的概率Rs=26%。用户每天的实际出发到达时间与理想的时间差Tg=7 min。合乘后平均每位用户每天的额外驾驶时间Te=7 min。
表5展示了通过VND获得的合乘方案相较于CAC的改进百分比,值为正表示得到改进,反之,则表示未得到改进。从总体上来看,通过VND获得的合乘方案,比CAC获得的合乘方案在各个指标下均有一定程度的改进。其中,Din平均改进17%,这说明VND 得到的合乘方案,合乘组内成员间距离更近。Rs平均改进31%,这说明VND 得到的合乘方案,合乘组内成员性别多为同性。Te平均改进28%,这与Din相一致,合乘组内成员距离越近,则用户的额外驾驶时间越短。
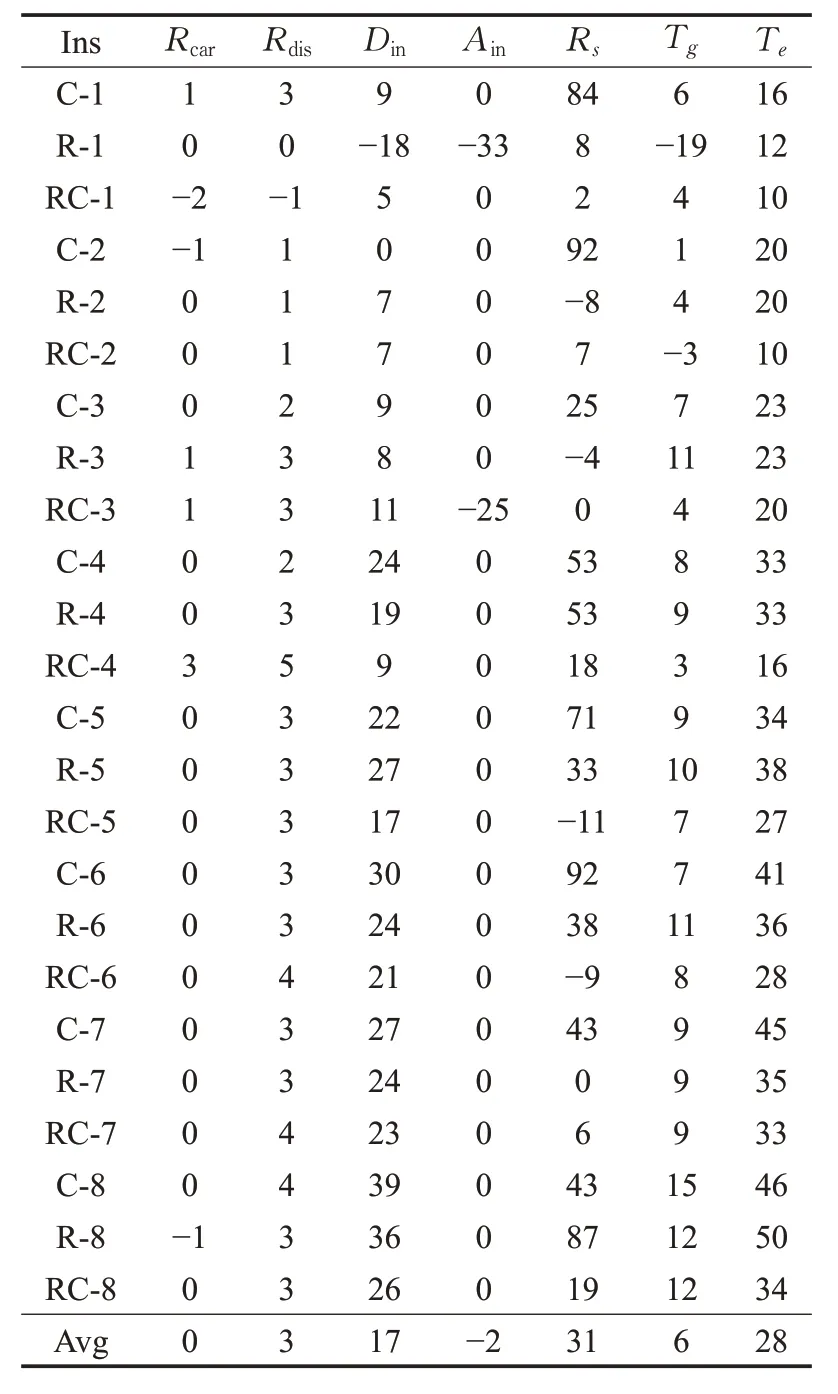
表5 与CAC对比结果
4.4.2效率分析
图9 展示了算法运行时间随用户数量的增长趋势。其中CAC为文献[16]中所提出的算法,DCAC是其在 Spark 上实现的分布式版本,DCAC(5 nodes)表示DCAC 在5 个节点集群上的运行时间,类似地,DCAC(10 nodes)表示集群节点个数为10。
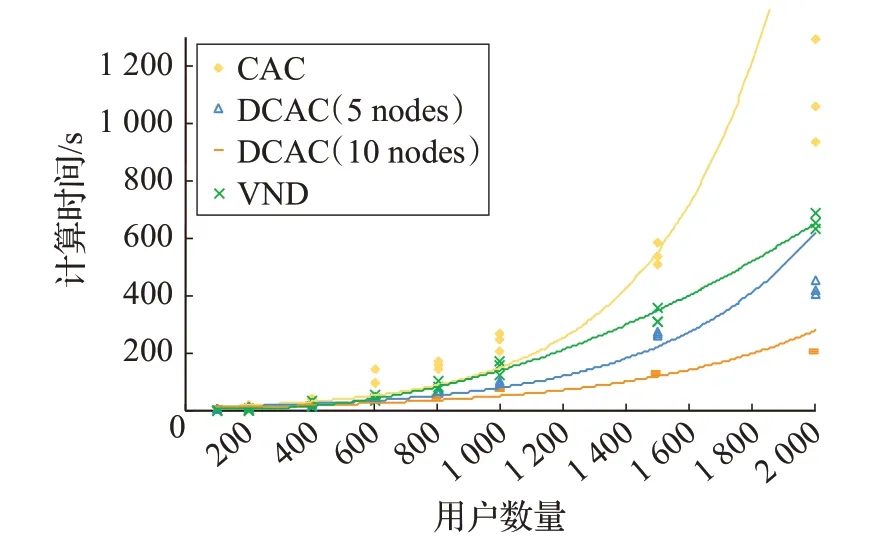
图9 算法运行时间
从图中可以看出,两种算法均随着用户数量的增加而增加。但很明显,VND 算法的运行时间远低于CAC算法,且VND 算法的增长趋势要比CAC 算法平缓很多,这说明无论是处理小规模问题还是大规模问题VND 算法都表现出了较优的性能。根据表4 中的实验结果可以计算得到,VND要比CAC平均节省55%时间。此外,从图中可以看出,对于用户数量少于600 的小规模实例,VND 的运行时间低于CAC 和DCAC。但继续增加用户数量,集群计算的优势开始显现,DCAC 的运行时间要比VND 运行时间短。因此,在计算资源充足的条件,相比较VND,采用DCAC对大规模问题求解具有更高的时间效率。而在单机环境下,VND 要比CAC表现更好。
4.4.3案例分析
为了更好地理解和说明提出的多目标优化模型和求解算法VND 如何为LTCPP 提供好的解决方案,以R-1为例进行案例分析。实例R-1包含100个用户,用户地理位置分布如图10 所示。通过VND 算法获得的分组结果如图11所示,其中,具有相同图案且用虚线连接的同户被分在同一个合乘组。图11所展示的分组即为合乘方案第一层信息,接下来再对合乘方案的第二层信息进行分析。
在合乘方案中,U1 单独出行(φ1=1),从图10可以看出,U1 距离其他用户较远,若将其与其他用户分配到同一个合乘组,接载U1 会导致合乘组成员的额外驾驶时间增加,可能会违反用户的最大驾驶时间约束,或导致目标函数值增加。因此,将用户额外驾驶时间作为优化目标,可以使得分布过于零散的用户偏向于单独出行,旨在提升所有用户的出行体验。出于相同的原因,U90、U71、U37 等用户也将单独出行。
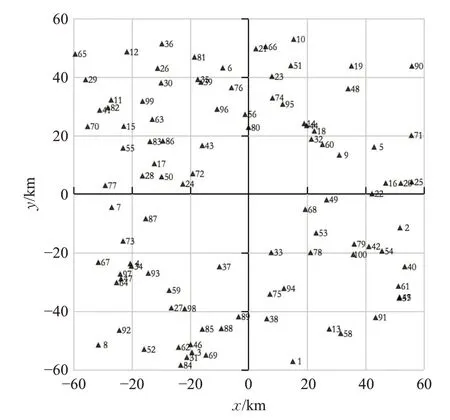
图10 R-1地理位置分布
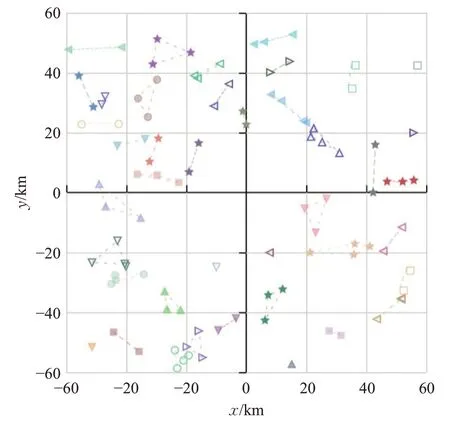
图11 R-1分组结果
从图11 可以看出,U38、U75、U94(φ38=φ75=φ94=0)为同一个合乘组,用户数据如表6 所示。当一个合乘组产生后,VND 算法首先会检查车容量约束。U38、U75、U94 的车容量均为4,而合乘组成员数量为3,所以没有违反车容量约束。
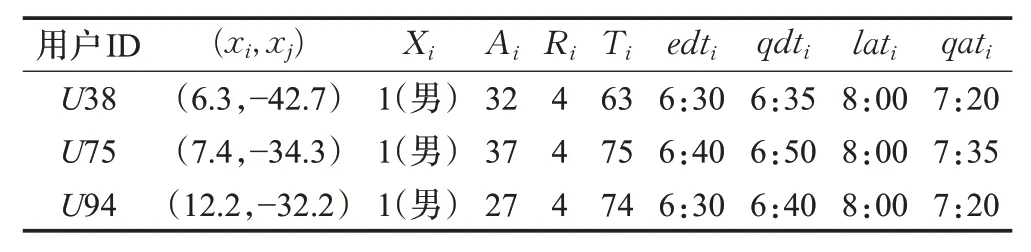
表6 用户数据
然后,为每个用户计算其担任司机时的最佳行驶路径,即求解赋权哈密顿回路最小化问题。按照3.2.3 小节提出的方法,可以得到U38、U75、U94 的最佳行驶路径。第一天,由U38 担任司机,最佳行驶路径为U38-U75-U94,第二天由U75 担任司机,最佳行驶路径为U75-U38-U94,第三天由U94 担任司机,最佳行驶路径为U94-U38-U75。之后3 人继续轮流担任每日的司机。详细的出发到达时间如图12所示。
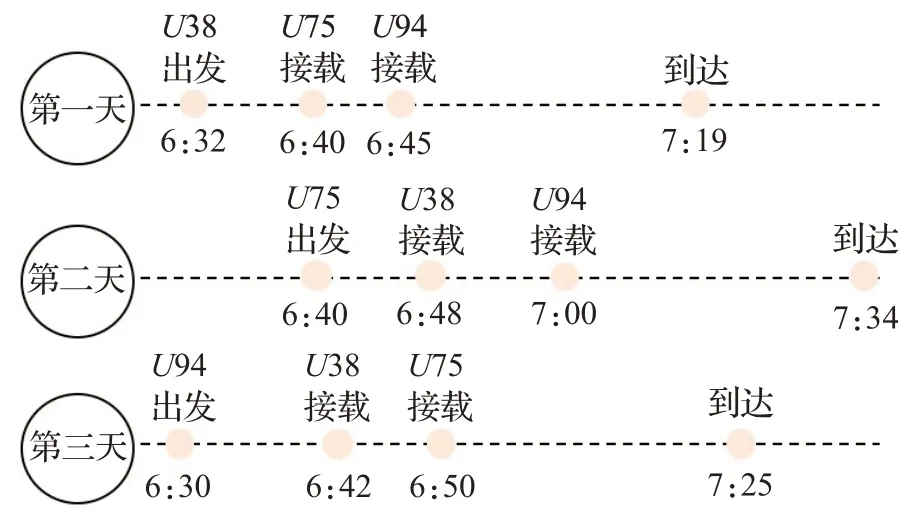
图12 出发到达时间
在计算用户最佳行驶路径,进行时间窗检查,包括:(1)出发/到达时间窗约束;(2)最大驾驶时间约束。从图12 可知,U38 每日实际出发时间依次为:6:42、6:48、6:32,其可接受的最早出发时间为6:30,满足出发时间窗约束。U38 每日实际到达时间依次为:7:25、7:35、7:19,其可接受的最晚到达时间为8:00,满足到达时间窗约束。U38 与目的地(坐标为(0,0))的距离为,驾驶时间等于43/1=43 min(行驶速度可按照实际情况进行调整)。与U75、U94 合乘后,U38 从自己的位置出发,依次接载U75、U94,再从U94 的位置前往目的地,所花费的时间为47 min,其可接受的最大驾驶时间为63 min,满足最大驾驶时间约束。同样的计算和检验方法应用于U75 和U94,只要其中有一位用户没有满足时间窗约束的行驶路径,该合乘组被视为无效合乘组,VND 算法会将该合乘组划分为两个小的合乘组,重复该过程,直到所有的合乘组满足时间窗约束。
接下来从用户与合乘组的距离、用户的额外驾驶时间、用户实际出发/到达时间与期望时间的差值、用户与合乘组平均年龄的差值以及合乘组用户性别分布情况来分析该合乘组的优劣。
U38 与合乘组的距离被计算为U38 与合乘组重心的距离,合乘组重心为(8.6,-36.3),则U38 与合乘组距离为6.8 km,U75 与合乘组的距离为2.3 km,U94 与合乘组的距离为5.5 km,则平均的用户与合乘组的距离为4.9 km。用户与合乘组的距离越大,说明合乘组成员间的距离越大,则用户所在合乘组每天行驶的里程数越多。因此,该值与合乘组每日行驶里程数具有正相关关系。U38 担任司机时总的驾驶时间为47 min,U75 担任司机时总的驾驶时间为54 min,U94 担任司机时总的驾驶时间为55 min,则该合乘组平均每天行驶的里程数为:52 km,该值会作为优化目标纳入到目标函数中,以减少合乘组每天行驶的里程数。
U38与目的地(坐标为(0,0))距离为43 km,所需要的驾驶时间为43/1=43 min(行驶速度可按照实际情况进行调整)。与U75、U94 合乘后,U38从自己的位置出发,依次接载U75、U94,再从U94 的位置前往目的地,所花费的时间为47 min。因此,参与合乘后,U38 的额外驾驶时间为4 min。同理,U75 的额外驾驶时间为19 min,U94 的额外驾驶时间为21 min,则平均的用户的额外驾驶时间为15 min。同样的,该指标以一定的权重作为优化目标纳入到目标函数中,旨在减少用户额外驾驶时间过长,导致用户满意度低。
U38 实际出发/到达时间与其期望的时间(6:35/7:20)的差值约为8 min。U75 实际出发/到达时间与其期望的时间(6:50/7:35)的差值约为8 min。U75实际出发/到达时间与其期望的时间(6:40/7:20)的差值约为9 min。平均的用户实际出发/到达时间与期望时间的差值为8 min。同样的,该指标以一定的权重作为优化目标纳入到目标函数中,旨在缩小用户出发/到达时间与其期望实际的差距,增加用户满意度,提升用户体验。
此外,组内平均年龄为32,U38 与组内平均年龄的差值为0,U75 与组内平均年龄的差值为5,U94 与组内平均年龄的差值也为5,则平均的用户与合乘组的年龄差为3。该指标同样以一定的权重作为优化目标纳入到目标函数中,旨在减少合乘组内用户的年龄差。该合乘组的成员全为男性,性别分布合理,在目标函数中为0,若为其他性别分布,则在目标函数具有一定的惩罚值,旨在增加同性别用户被分在一个合乘组的几率,这是出于用户出行安全的考虑。
需要说明的是,该案例中用户与合乘组的距离和用户的额外驾驶时间比表4中的对应指标的平均值大,这是由于实例R-1中的用户属于随机分布,相对于集中分布和混合分布,随机分布的用户地理位置过于分散,用户间距离较大,从而导致这两个值增大。
鉴于篇幅限制,以合乘组(U38、U75、U94)为例进行了分析,其他合乘组分析方法相似。
5 结论
目前,我国城市交通拥堵严重,并由此导致一系列问题,严重影响了城市居民的生活质量。而车辆合乘可以在现有资源条件下有效减少私家车出行数量,从而缓解交通拥堵问题。针对LTCPP,本文首先构建了基于用户满意度的带有车容量和时间窗约束的多目标优化模型,并通过随机森林算法确定各优化目标的权重,旨在解决人为设定权重因子主观性太强的问题。然后,提出了解决LTCPP的VND算法。实验结果表明,采用VND算法获得的解决方案,每日私家车出行量可以减少72%,每日行驶的总里程数减少67%,合乘成员通常分布在半径为2.4 km的圆形范围内,合乘组成员平均年龄差在5 岁左右,同性被分到同一个的概率在26%,用户实际出发到达时间与期望的时间差7 min 左右,用户需额外驾驶时间在7 min左右。从时间效率上来看,VND算法相较于CAC 可以节省55%的时间。因此,结合随机森林算法和VND算法能为LTCPP高效得提供高质量的解决方案。

