遗传算法与行人疏散模型结合的建筑出口优化
韩雨烔,王维莉,范勤勤,胡志华
上海海事大学 物流研究中心,上海 201306
1 引言
随着经济社会的发展,城市化步伐加速推进的同时伴随着城市人口数量的不断攀升,许多功能多样、结构复杂的建筑综合体应运而生,大规模人群聚集成为当今社会的普遍现象,然而近年来密集人群由于缺乏有效管理、控制而引发的行人踩踏事故频发,不仅对人民的生命财产造成巨大损失,而且给城市公共安全带来严重威胁。当火灾或其他突发事件发生时,建筑或特定区域内的人员需要尽可能快的逃离危险区域,如何确保人员的生命安全以及疏散过程的高效性是公共安全领域的核心目标。因此,对建筑设施进行合理设计、布局,对提高行人疏散的效率、保障人民生命安全具有重大意义。作为建筑疏散的关键设施,出口的合理布局尤为关键。褚冠全等[1]利用GridFlow 疏散模型研究疏散出口宽度对人员疏散的影响,发现对于较宽的疏散出口条件,当疏散准备时间服从正态分布时,总的疏散时间也服从正态分布。宋卫国等[2]采用社会力模型研究群体疏散过程,不仅重现了实际疏散过程中的典型现象,而且分析了出口宽度、出口厚度等建筑结构特征与疏散时间的关系。Zhao 等[3]通过建立元胞自动机模型模拟出口处疏散的动态过程,得到了有利于疏散的出口宽度及出口间隔,并研究单出口和双出口对疏散时间的影响,发现建筑空间的疏散出口对称时各个出口的疏散效率相同,进而可以缩短整体疏散时间。Zhao 等[4]将行人的心理和行为融合到元胞自动机模型,应用于疏散场景,研究认为出口宽度必须大于某个临界值,出口间隔的最优值与出口宽度无关,但与建筑物的总宽度有关,采用对称的出口布局更有利于疏散效率的提高。Sticco等[5]运用社会力模型对单室双出口场景下同侧墙两出口间距与疏散效率的关系进行研究。结果表明两个出口的间距在一定范围内不仅不会提高疏散效率,反而会产生“快即是慢”的现象。Alizadeh[6]提出了一种动态的元胞自动机模型来模拟具有障碍物的空间疏散过程,分别考虑了疏散人员的心理,出口位置、宽度及障碍物的位置等基本参数,认为疏散人员的初始分布在获得的结果中起着重要作用。Tian等[7]通过构建改进的动态场域模型来模拟疏散行人间的交互作用,真实地再现了拥堵过程中前方行人的阻挡效应,同时研究了无障碍房间内出口宽度及位置对疏散时间的影响。Takimoto等[8]研究了行人从单出口大厅疏散的过程,分析了行人在大厅内初始分布位置和最终疏散时间的时空分布关系,并指出二者有很强的关联性。Cao等[9]提出了一种扩展的多网格模型来研究双出口房间在火灾情境下的疏散问题,对火灾发生过程中出口选择行为展开研究。讨论了不同疏散人员类型,效用阈值和疏散准备时间对疏散过程的影响。胡凯等[10]以地铁站为研究对象,运用仿真软件从地铁站出入口数量、楼梯宽度等方面对人群疏散进行模拟研究,通过与设计规范对比发现楼梯的设计是疏散过程的瓶颈。以上研究均将行人在疏散过程中的运动特征进行量化建立了行人运动仿真模型,针对有限出口的布局场景进行动力学分析以及空间疏散能力评估,从而得到较优的出口布局。然而采用基于最优化的方法生成优化的疏散出口布局的研究依然很少。王付宇等[11]从地铁站人员应急疏散的仿真研究、不同规则下疏散模型的研究和智能算法在疏散建模中的应用三个角度对突发事件下地铁站人员应急疏散问题进行综述,提出了把建筑设施因素引入地铁站人员应急疏散问题中,并利用改进的蚁群算法求解最优疏散路径。姜立等[12]通过对社会力模型进行修正建立人群疏散仿真模型,同时采用遗传算法优化障碍物设置,研究发现优化结果不仅有效提高疏散空间内人群的逃生效率而且对建筑设计也有一定启示。Zhao 等[13]通过在出口前适当放置障碍物来改善恐慌情况下的行人流量,同时采用差分进化算法实现不同形状障碍物几何参数的优化,获得最优疏散效率。研究发现障碍物的所有几何参数都会显著影响行人的疏散效率,同时证明相比于柱状障碍物,板状障碍物更有助于提高疏散效率。Kurdi等[14]利用模拟退火算法和深度优先搜索技术来优化多个出口的最优分布。通过设计疏散系统研究疏散环境中出口及障碍物的分布对行人疏散效率的影响,并采用多种出口布局进行测试。结果表明,出口的相邻排布会导致出口前拥堵程度的增加,采用深度优先搜索技术作为疏散策略,会延长疏散时间。Abdelghany等[15]在基于遗传算法的疏散优化框架中集成元胞自动机仿真模型,解决了多出口的大规模场景下非均匀分布人群的疏散策略问题。
本文构建宏观-微观双层优化框架,在宏观层通过遗传算法连续优化生成最有利于疏散的空间布局,在微观层以行人运动仿真模型模拟该空间布局下人群的疏散动力学过程。与传统启发式优化相比,本文提出用疏散仿真结果替代适应度函数,对可行解的评价更加准确,可以得到更加合理的优化结果。该优化框架可以为建筑空间布局设计、应急疏散方案规划提供理论和方法支持。
2 模型框架
2.1 行人运动仿真模型
本文的行人运动仿真模型基于社会力模型建立[16-17],该模型以牛顿力学为基础,引入“社会力”的概念将行人个体运动的内在和外在驱动力分为个体与目标、个体与其他个体、个体与环境的交互。基于牛顿第二定律,质量为mi的行人i期望以速度,朝着目标方向进行疏散,表现为目标驱动力,用表示。在实际疏散过程中假定行人i在时间τi内将实际速度vi调整至,目标驱动力计算公式如(1)所示。同时,行人i在疏散过程中会尽量与其他行人及障碍物保持一定的安全距离,分别用作用力fij和fiw来表示。因此时间t内速度的变化可以用公式(2)所示的动力学方程描述。位置si(t)的改变由速度vi(t)给出。

通常行人在运动过程中会与其他行人保持一定的距离,用心理排斥力来表示,其中Ai、Bi为常数;表示行人i和行人j间的距离;rij=(ri+rj)表示行人i和行人j的半径之和;(si-sj)/dij表示由行人j指向行人i的单位向量;当两个人的距离小于二者半径之和时,会因为肢体接触而产生接触排斥力,接触排斥力由两部分组成,分别为行人间的身体排斥力k(rij-dij)nij和滑动摩擦力κ(rij-dij)Δ,其中k、κ为常数;表示与nij垂直的单位向量;为行人间切线方向的速率差。由此行人间的相互作用力fij可以表示为公式(3):

人与障碍物的相互作用力fiw的表达式与fij类似,可表示为公式(4),其中diw表示行人i到障碍物w的距离,niw表示垂直于障碍物的方向,tiw表示与障碍物相切的方向。

基于文献[16-17],本文行人运动仿真模型的参数如表1所示。

表1 社会力模型参数
2.2 基于遗传算法与行人运动仿真模型的双层优化框架
疏散出口的布局优化问题具有非线性的特点,本文建立基于遗传算法与行人运动仿真模型的双层优化框架,计算获取最有利于人员疏散的出口布局策略。上层模型利用遗传算法构建疏散出口布局的优化模型,输出不同条件下出口位置的备选集合,输入到下层行人运动仿真模型中,用人群疏散动力学过程的模拟结果替代传统遗传算法中的适应度函数,评估不同出口布局染色体下的适应度值,从而引导随机搜索的方向。其中遗传算法部分采用实数编码方式,染色体长度等于决策变量的个数,本文根据空间布局的不同,取出口位置的横坐标或纵坐标为染色体的组成部分,遗传算法的参数设置如表2所示。

表2 遗传算法的参数设置
基于遗传算法与行人运动仿真模型的双层优化流程如图1所示。首先随机生成初始种群,种群中的每个染色体代表一种出口位置布局,接着使用行人运动仿真模型模拟该出口布局下的人群疏散动力学过程,获取疏散完成时间作为对应染色体的适应度值进行评估。以疏散时间最小化作为遗传算法迭代优化的方向,根据各个染色体的适应度值,采用轮盘赌的方法进行选择操作,使优化个体大概率遗传到下一代;为了对编码生成的解集空间进行高效搜索,通过交叉和变异操作,将两个相互配对的染色体以交叉率0.8 交换部分基因,从而形成两个新的个体;然后采用均匀变异的方法,设置较大的变异率0.2,使种群中染色体的某个基因位发生突变,形成新的个体;继续对新生成的染色体进行适应度评价;最后重复执行选择、交叉和变异3种操作,直至发现最优解或到达设定的迭代次数,最终输出人群的最短疏散时间以及最有利于疏散的出口位置坐标。

图1 基于遗传算法与仿真模型的双层优化流程图
3 场景测试及结果讨论
3.1 仿真环境
单室是建筑内人员分布的最小单元,其安全出口是在紧急情况下人员疏散的重要通道。根据GB 50016—2014《建筑设计防火规范》的规定,公共建筑内房间疏散门的数量应经计算确定且不少于两个[18]。因此将仿真环境设置为带有两个出口的12 m×12 m的房间,其中两个出口的宽度分别为DW1和DW2,假定DW1= DW2且取值范围为0.8~1.6 m。设置3种典型的出口布局:两个出口设置在同一侧,两个出口设置在相邻侧,两个出口设置在相对侧,如图2所示。

图2 3种典型的出口布局
人员在房间内的初始分布见图3(以100 人为例),考虑不同密度情况,安排人员数量分别为49、100、196人(即人员分布密度为0.5人/m2、1人/m2、2人/m2)。假设场景内所有人员同时开始疏散,且均可看见所有出口,并且选择与个体当前位置距离较近的出口进行疏散。

图3 人员初始分布图
3.2 两个出口在同侧的出口位置优化
3.2.1最优出口的位置
基于前述条件,采用遗传算法对该场景布局下的出口位置进行优化,为了更加直观地表示优化后两个出口的空间位置分布,引入变量Δs来表示两出口之间的距离,在该场景下即为图2(a)中的DL。不同出口宽度、行人大小以及行人密度下所对应的两个出口最优位置间的距离,如表3所示。

表3 不同条件下两出口最优分布间距
根据表3 数据得到图4,为部分行人半径和密度下以疏散时间最短为目标获得的优化的出口位置,图4(d)表示疏散人群密度相同时,在该场景布局下行人半径对于最优出口位置的影响。随着出口宽度的增加,当行人半径r=0.2 m 时,两个出口的最优位置逐渐向墙中间靠拢(见图4(a)),因此人员到出口的距离可能是影响疏散效率的主要原因;当行人半径r=0.3 m 时,优化的两个出口位置始终处于同一侧墙的两端(见图4(b)),在这种情况下即使场景内只有100个人,此时人员在疏散过程也会呈现较拥挤的情况,为避免两个出口在中间所引发的“羊群效应”,出口分布在墙两侧可能更利于疏散分流从而减少疏散时间。当行人半径r=0.25 m 时,出口一的优化位置始终在靠近下侧墙的一端,出口二的优化位置随着出口宽度的增加逐渐向中间靠拢(见图4(c))。
优化疏散结果如表4 所示。为评价出口布局优化结果,本文提出优化率(IP)评价指标,计算公式如式(5):

其中,TORE为初始布局下人群疏散完成时间,TOPE为优化后人群疏散完成时间。初始布局为遗传算法生成的初始种群中的最优的出口布局。
3.2.2行人身形尺寸对疏散效率的影响
考虑到性别、年龄以及种族的差异,行人个体的身形差异明显。本文行人运动仿真模型以圆形表示行人个体,分别取半径(下述均用r表示)为0.2 m、0.25 m、0.3 m 时,采用遗传算法对不同身形大小行人条件下的出口位置进行优化。图5 分别为场景内初始行人分布密度为0.5人/m2和2人/m2时的疏散时间变化,随着出口宽度的增加,疏散时间整体均呈现下降趋势;图5(a)、(b)中的折线均无重叠或交错情况,并且在出口宽度相同时,随着行人半径的增大疏散时间也随之增加,验证了行人半径的增加对于会降低疏散效率;当行人密度为0.5 人/m2时,r=0.2 m 和 0.3 m 时,随着出口宽度的增加,疏散时间下降明显,由此可以看出此时出口宽度是影响疏散时间的主要因素;当r=0.2 m,在出口宽度由0.8 m增加到0.9 m时疏散时间下降明显,然而此后随着出口宽度的增加,疏散时间基本不变,保持在8.09 s 左右,可以看出在此时出口宽度不再是影响疏散效率的主要因素,因此出口宽度0.9 m 在此情况下为一个临界宽度。根据上述分析可以得出,疏散出口宽度与疏散效率整体呈正向关系,疏散人员半径与疏散效率呈负向关系。

图4 两出口在同一侧的最优位置分布

表4 不同疏散条件下的疏散优化结果
3.2.3行人初始密度分布对疏散效率的影响
如图6 所示,无论r=0.2 m 还是0.3 m ,随着出口宽度的增加,整体疏散时间大致呈下降趋势;同时在出口宽度固定的情况下,随着行人密度的增加,疏散时间增加,对疏散效率具有负向影响。由图6(a)当r=0.2 m时,出口宽度由0.8 m增加到1.6 m在3种行人密度下疏散时间缩短1 s 左右,出口宽度不再是影响疏散效率的主要因素;由图6(b)当r=0.3 m 时,行人密度为2人/m2的疏散时间曲线始终与密度为0.5人/m2时差异明显,即使在出口宽度为1.6 m时,疏散时间依然相差3.44 s。根据以上得出行人初始密度与疏散效率呈负向关系,降低行人密度对于疏散效率的提高影响显著。
3.3 两个出口在相邻侧的位置优化
对该出口布局下疏散出口位置进行优化,此时表示两出口之间距离的变量,见图 2(b)。行人初始密度为1人/m2情况下,不同出口宽度、行人半径所对应的两个出口的最优位置分布,如图7所示。
其中图7(a)的纵坐标为Δs,在不同行人半径下两个出口的最优位置分别与右边墙及下边墙的距离差异不大;图7(b)~(d)表示不同行人半径下两个出口的最优位置在相邻侧的分布情况。当行人半径r=0.2 m时,随着出口宽度的增加两个出口的最优分布相对平稳,大致处于两侧墙中心线偏右的位置。当行人半径r=0.25 m时,出口宽度为0.8 m时,两出口的最优位置靠近左边墙和上边墙,可以看出在出口宽度最小的情况下该出口分布可实现最大程度的人群分流,从而避免出口前人群拥堵而造成的疏散时间延长;随着出口宽度的增加,两个出口的位置均向下边墙和右边墙的中心线方向移动,但均分布在中心线偏右位置;当行人半径r=0.3 m时,两个出口的分布随着出口宽度的增加变化幅度较大,当出口宽度小于1 m时两出口的最优位置为该场景的右下角,当出口宽度大于等于1 m时随着出口宽度的增加,出口位置由靠近左边墙和上边墙下边墙和右边墙的中心线方向移动,最终优化的出口布局大致停留在中心线的位置。

图5 不同行人初始密度分布下的疏散时间变化

图6 不同身形半径人群的疏散时间

图7 两出口分布在相邻侧的最优位置分布
3.4 两个出口在相对侧的位置优化
对该出口布局下疏散出口位置进行优化,两出口之间的距离的变量,见图 2(c)。图 8 为行人初始密度为1人/m2的情况下不同出口宽度、行人半径所对应的两个出口的最优位置分布。
与上节场景的分析类似,由图8(a)得出在不同行人半径及出口宽度下,出口的最优位置分布的距离相比于上一场景差异更小,因此相对侧出口位置的对称性是影响疏散时间的重要因素。如图8(b)所示,当行人半径r=0.2 m时,随着出口宽度的增加,两个出口的位置均在接近上边墙和下边墙中心线的位置左右平稳波动,此时疏散人员与出口的距离为影响疏散时间的重要因素。如图8(c)所示,当行人半径r=0.25 m时,随着出口宽度的增加,两个出口的优化位置均由上下边墙中心线的右侧向左接近中心线。如图8(d)所示,当r=0.3 m 时,在不同出口宽度下,出口的最优位置基本分布在上下墙中心线与右边墙之间的中间位置。
3.5 出口优化布局场景的疏散效率分析

图8 两出口分布在相对侧的最优位置分布
图9为不同出口布局下对于3种典型疏散场景的疏散时间的比较情况,图9(a)的场景中人员半径最小且人员数量最少,当两个出口位于同一侧时,随着出口宽度的增加,人群疏散时间在出口宽度为0.9 m 之后几乎不变,在两个出口位于相邻侧和相对侧的布局中,人群疏散时间一直呈下降趋势,其中在两个出口位于相对侧布局中的下降趋势最为明显,计算得到的最小疏散时间为5.66 s。图9(b)的场景中人员半径最大且人员数量最多,当两个出口位于同一侧时,随着出口宽度的增加,人群疏散时间几乎没有变化,而在两个出口位于相邻侧和相对侧的布局中,人群疏散时间呈下降趋势,且在两个出口位于相对侧布局中的变化趋势最为明显,疏散时间由65.09 s 下降至17.19 s,下降幅度为47.9 s。在出口宽度为0.8 m时,3种布局的疏散时间差异最为明显,分别为65.09 s、41.1 s、17.16 s,并且随着出口宽度增加,这种差异逐渐缩小。图9(c)的场景中人员半径为0.25 m,人员密度为1人/m2,可以看到随着出口宽度的增加3种布局下的疏散时间均呈下降趋势,其中在两个出口位于同一侧布局中的下降趋势最为平缓,疏散时间由12.15 s减少至9.33 s,在两个出口位于相对侧布局的下降趋势最明显,疏散时间由22.83 s 减少至9.3 s,并且3 种布局疏散时间差异随着出口宽度的增加而减少。因此,认为疏散出口的宽度变化对于两个出口位于相对侧的布局的疏散效率影响最大。
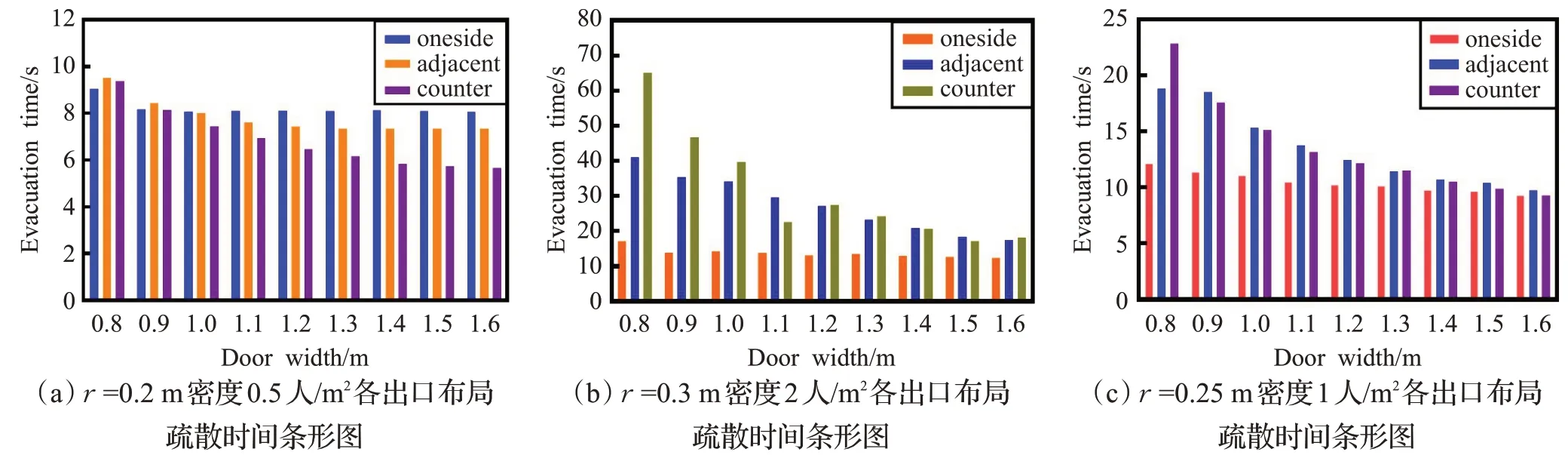
图9 3种出口布局下的疏散时间条形图
4 结束语
本文在基于遗传算法的优化模型下集成行人运动模型形成宏观-微观双层优化框架,以疏散时间最短为目标获得了不同布局下出口的最优位置分布,分别讨论了出口宽度、疏散人员半径、疏散人员密度、出口布局对于人群疏散效率的影响。结果表明:(1)疏散出口宽度与疏散效率呈正向关系;疏散人员半径、人员密度与疏散效率呈负向关系。(2)疏散场景内行人初始密度为1 人/m2时,随着出口宽度的增加,不同疏散人员半径所对应的场景布局中的最优出口分布呈现一定规律性。在两出口位于相对侧的布局中,疏散出口位置的对称性为影响疏散效率的重要因素。(3)疏散出口的宽度变化对两出口位于相对侧布局的疏散效率影响最大,对两出口位于同一侧布局的疏散效率影响最小。

