物理学优化的密度峰值聚类算法
贾 露,张德生,吕端端
西安理工大学 理学院,西安 710054
1 引言
2014 年,《Science》上发表了题为《Clustering by Fast Search and Find of Density Peaks》[1]的论文。首次提出了密度峰值聚类算法(DPC),与DBSCAN 算法[2]、AP算法[3]、K-Means算法[4]等经典的聚类算法相比,该算法能够发现任意形状的类簇,不仅能够自动确定类簇质心,而且使剩余样本点的分配更加快速高效。该算法已被成功地应用于多文档文摘聚类[5]、场景图像分类[6]、社交网络中社交圈的发现[7]等诸多领域。但是该算法自身也存在着一定的问题:(1)在局部密度的计算过程中需要人为设置截断距离,存在人为参与的随机因素;(2)对于剩余样本点采用“一步分配”策略,虽然该策略简单、高效,但是会导致剩余样本点的分配不够精准,易引起“多米诺骨牌”效应。
针对DPC算法存在的不足之处,薛小娜等[8]提出了结合K近邻改进的密度峰值聚类算法,该算法利用K近邻的思想设计全局分配策略;王洋等[9]提出了自动确定类簇中心的密度峰值聚类算法,该算法基于基尼指数自适应的确定截断距离及自动获取类簇质心;金辉等[10]提出了自然最近邻优化的密度峰值聚类算法,该算法采用自然最近邻的思想优化局部密度,并提出一种新的类簇间相似度来解决流形数据问题;Liu 等[11]提出了基于K近邻聚类策略的自适应密度峰值聚类算法,该算法通过K近邻的密度峰来计算截断距离和局部密度,并自动选择初始聚类中心的新方法,若聚类可达,则继续进行聚类;Wang 等[12]提出了基于数据场理论的密度峰值聚类算法,该算法引入了信息熵的概念,借此来优化密度峰值聚类算法中的截断距离dc,避免了该参数根据经验来设定所导致的随机性;谢娟英等[13]提出了K近邻优化的密度峰值聚类搜索算法(KNN-DPC),该算法通过引入K近邻的思想,重新定义样本的局部密度,采用两步分配的策略对剩余样本点进行分配,但是该算法对近邻数k值的选取较为敏感;Xie等[4]又提出了模糊加权K近邻优化的密度峰值搜索聚类算法(FKNN-DPC),该方法针对KNN-DPC 中的两步分配策略进行改进,采用模糊隶属度来判断样本属于哪一个类簇;蒋礼青等[14]提出了快速搜索与发现密度峰值聚类算法的优化,该算法根据近邻距离曲线来自动的确定截断距离dc,利用衡量参数解决了类合并后无法撤销的难题,实现了对多密度峰值数据的正确聚类。
上述几种改进算法虽然都具有较好的聚类效果,但是并未实现数据自发的聚合与离散。本文在DPC算法的基础上进行改进,提出了一种物理学优化的密度峰值聚类算法W-DPC。
2 DPC算法
DPC算法设计的主要思想:类簇质心的局部密度高于周围邻居的密度,而且与密度较高点的距离都比较大。该算法思想的实现主要运用了两个概念:样本的局部密度和样本的距离(这两个概念正好对应算法的两个假设)。假设:(1)类簇质心被低密度的邻域所包围;(2)类簇质心与比它密度更大的数据点之间的距离更远。在这里,假设S为待聚类的数据集。
对于样本i,局部密度ρi的定义有两种方式,第一种是:

其中:

dij代表样本i和样本j之间的距离,为截断距离(需要事先人为确定)。
由于式(1)估计样本的局部密度可能会受到统计误差的影响,且该式适合于对离散的数值进行计算,故采用第二种,即式(3)估计连续值样本的局部密度:

对于样本i,其距离定义为:

观察上式可以看出:如果样本i的局部密度是最大的,那么该样本的距离是该样本到其余所有样本之间的最大距离;否则,该样本的距离是该样本和它距离最近且密度高于它的样本距离。也就是说,局部密度越大的样本其距离越大,因此,DPC 算法将密度较大和距离较大的样本选作类簇质心。
DPC 算法提出了决策图的概念和一步分配策略。决策图是将样本的密度ρ和距离δ分别作为x轴和y轴构成的一个二维空间,故决策图右上角的点选作为类簇质心。一步分配策略就是将剩余的样本分配到与它距离最近且密度比它高的类簇中。
3 本文算法
3.1 定义描述
本文算法利用物理学中的万有引力定律[15]和第一宇宙速度对DPC 算法进行改进,重新定义了算法的局部密度以及分配策略,现将本文相关概念定义如下。
定义1 样本a的邻域其中S表示数据集,表示样本a和b之间的距离,r表示扫描半径。
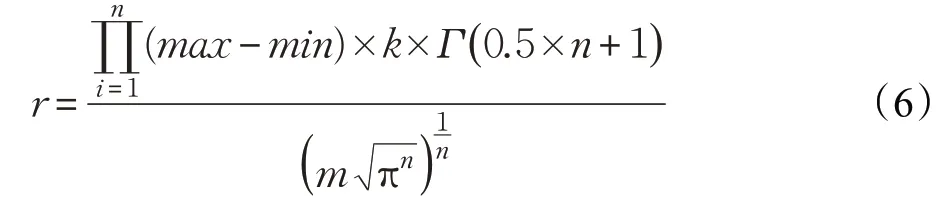
参数m、n表示数据集的行数与列数,max表示数据集的最大值,min表示数据集的最小值,k表示类簇中最少包含的样本数目。
定义2 样本a的质量:

考虑到样本a所处的局部情况,这里将样本a的邻域,其周围邻居的个数作为质量。
定义3 样本a的吸引力:
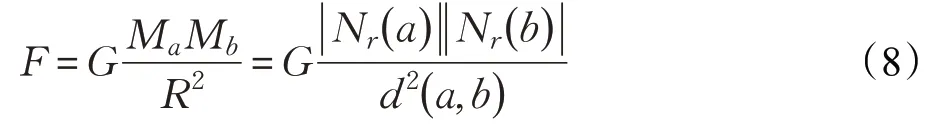
任何物体之间都存在着相互吸引力,将吸引力作为衡量样本的局部密度,如果距离越小,则吸引力即局部密度越大;距离越大,局部密度越小,增大了样本之间的密度差异,提高了样本的质量,易于识别高密度样本点且有利于确定类簇质心。
定义4 样本a的第一宇宙速度:

其中Mc是类簇质心c的质量,Rac是样本a到类簇质心c之间的距离。对于聚类而言,如果将类簇的质心比作地球,那么样本就相当于其他星体。如果一个样本属于某个类簇,那么该样本对于该类簇质心的速度就比较大,从而,该样本就越不容易脱离该类簇对其的吸引力,相反,如果一个样本不属于某个类簇,则样本对于该类簇质心的速度就比较小,很容易脱离类簇质心对它的吸引。
3.2 算法步骤
本文算法主要分成六个步骤完成:
算法1 W-DPC算法
输入:数据集S,类簇中最少包含的样本数目k
输出:聚类结果
1.对原始数据集进行标准化处理。
2.根据公式(8)计算样本的局部密度,根据公式(4)和(5)计算样本的距离。
3.根据上述计算的结果,以样本的局部密度为x轴,样本的距离为y轴构造决策图。
4.选取决策图右上角的点作为数据集的类簇质心,选取点的个数作为数据集的类簇数目。
5.根据算法2对剩余必须属于的数据点进行分配。
6.根据算法3对剩余可能属于的数据点进行分配。
算法2 必须属于数据点的分配
1.从类簇集合当中随机选择一个未被分配的样本数据点a。
2.根据公式(9)计算a与每一个选定的类簇质心之间的第一宇宙速度。
3.如果a与每一个类簇质心计算的第一宇宙速度不相等,则将该样本数据点归属于第一宇宙速度计算值最大的类簇;否则将该数据点归属于可能属于的样本数据点集。
4.重复上述的分配步骤,直到每一个未被分配的样本数据点皆被访问过。
算法3 可能属于数据点的分配
1.将扫描半径按照步长为0.1进行自增操作。
2.从可能属于的样本数据点集中随机选取一个样本数据点,执行算法2的第2、3步。
3.重复算法3的第1、2步。
4.所有的样本数据点全部分配,算法结束。
W-DPC算法的流程图如图1所示。
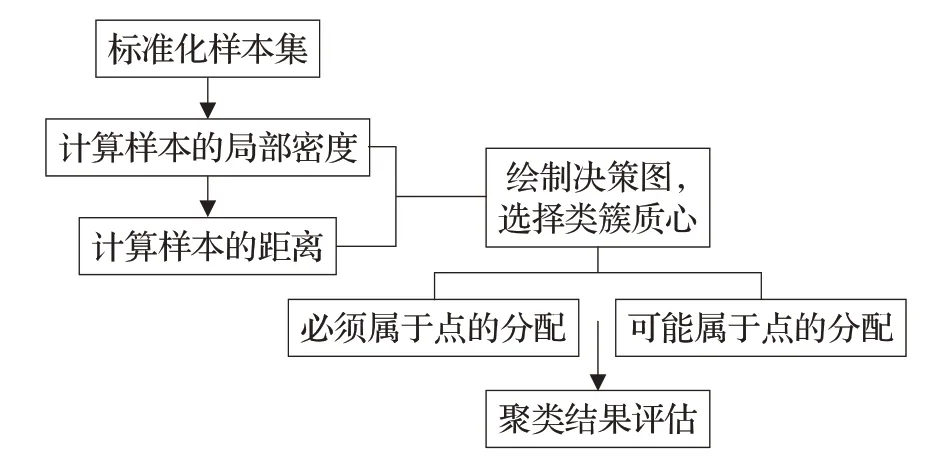
图1 W-DPC算法
3.3 算法复杂度分析
假设数据集的规模为n,W-DPC 算法存储每个样本到类簇质心的距离以及分配策略中的识别矩阵,但是增加的空间复杂度不超过,其中m代表类簇质心集合且m通常较小,因此,W-DPC算法的空间复杂度与DPC算法空间复杂度的量级相同。
W-DPC 算法的时间复杂度主要来源于四部分:(1)计算样本之间的距离,时间复杂度为Ο( )n2;(2)计算每一个样本的局部密度Ο( )n2,万有引力计算中使用的距离是前面已经计算过的距离矩阵;(3)计算每一个样本的δ距离,时间复杂度为Ο(n2);(4)分配样本:时间复杂度为其中k1代表必然属于点的规模,k2代表可能属于点的规模,所以总的时间复杂度为虽然W-DPC 算法的时间复杂度大于传统的DPC 算法,但是算法在运行上进行很好地优化,故数据集上的实际运行时间不像预期的那么大。
W-DPC 算法利用物理学公式重新定义局部密度,不仅到考虑样本周围的情况,而且有助于精准识别高密度样本;将剩余样本分为必须属于点及可能属于点两种不同情况,针对不同的情况,采用不同的分配策略,能够提高剩余样本的分配精度,且实现数据自发的聚合与离散,更好地体现了两种不同学科之间地交叉与融合。
4 实验结果及其分析
对数据集进行预处理,消除缺失值和维数差异的影响,采用相同维度的所有有效值的平均值替换缺失值。对于数值范围上的差异,使用公式(10)将所有数据线性地映射到[0,1] 范围,提高计算效率。
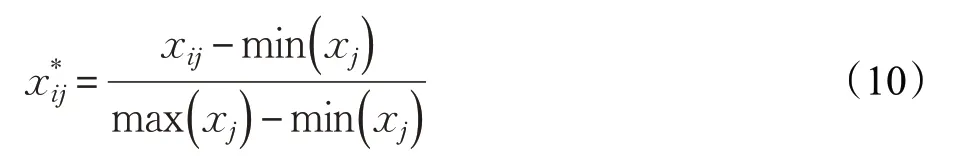
为了验证W-DPC 算法的有效性和可行性,将W-DPC算法分别与KNN-DPC算法、DPC算法、DBSCAN算法、AP 算法、K-Means 算法在人工合成的数据集Flame People、Spiral People 以及 UCI 上的真实数集进行实验评估,在所有的实验中,距离度量都使用欧氏距离。使用的数据集在表1进行了展示,包括数据集的名称、规模、维度以及类别数。
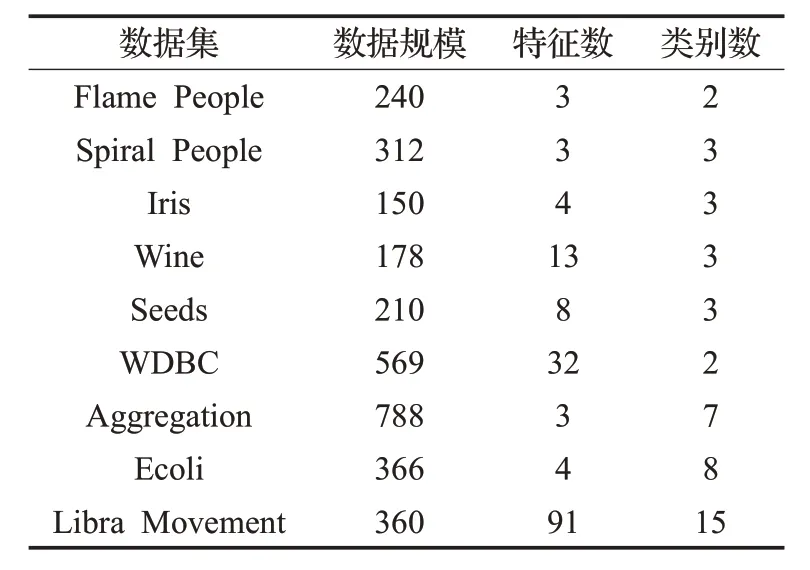
表1 人工合成数据集以及UCI数据集
4.1 实验设计
本文使用调整兰德系数(ARI)、调整互信息(AMI)、FM指数(FMI)等[16-18]三个评价指标。
兰德指数(Rand Index,RI)需要给定实际的类别信息C,假设C*是聚类所产生的结果,a表示在C和C*中都是同一个类别的元素对数,b表示在C和C*中都是不同类别的元素对数,那么RI为:

但是对于随机结果,RI 并不能保证分数接近于零,故为了实现“在聚类结果随机产生的情况下,指标应该接近零”,调整兰德指数ARI被提出,ARI是具有更高的区分度:
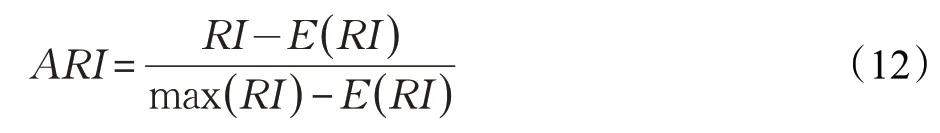
父亲什么时候回来的,我不知道。第二天我醒的时候,父亲坐在床边,问我昨晚的事,我只好如实说了。他对我讲,不能把这事再告诉任何人,包括祖父。我说为啥啊。“如果别人知道了,咱家的粮食就不够吃了,就要挨饿,懂吗?”我没有说话,坚定地点了点头。
AMI是一种有用的信息度量,它是指两个事件集合之间的相关性,类似于ARI,内部使用的是信息熵:
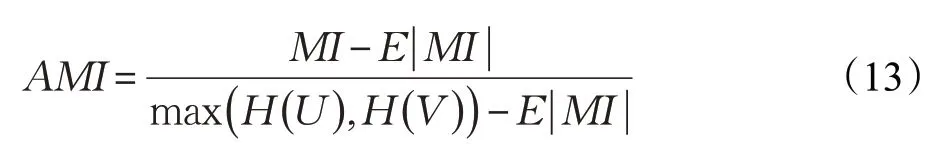
利用基于互信息的方法来衡量聚类效果所需要实际类别的信息。AMI 的取值范围是值越大意味着聚类的效果越好,也就是说数据之间分布的相似度越高。
FMI是成对精度与召回率的几何均值:

假设通过聚类划分的簇为C*,参考模型给出类簇的划分结果为C。其中a表示在C*中属于同一个类别且同时在C中属于同一个类别的样本对数量;b表示在C*中属于同一个类别但是在C中属于不同类别的样本对数量;c表示的是在C*中属于不同的类别但是在C中属于同一个类别的样本对数量。
4.2 实验结果
针对表1给出的人工合成数据集,首先利用W-DPC算法与KNN-DPC 算法、DPC 算法、DBSCAN 算法、AP算法、K-Means 算法进行比较,图2 给出了这六种算法在Flame People 数据集上聚类的效果图。
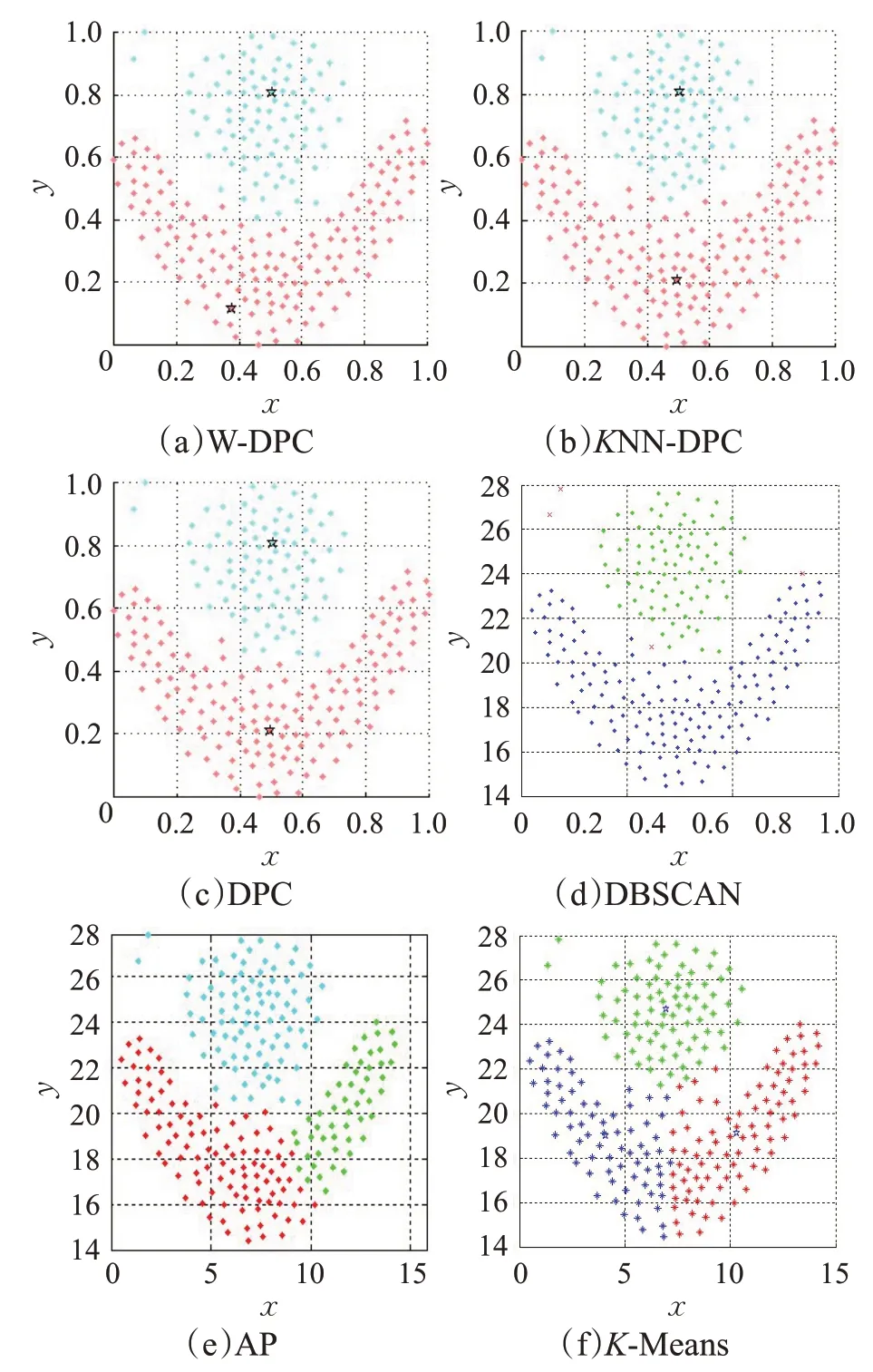
图2 六种算法在Flame数据集上的聚类效果图
如表2 列出了三种评价指标的结果;如图3给出了评价指标之间的比较。
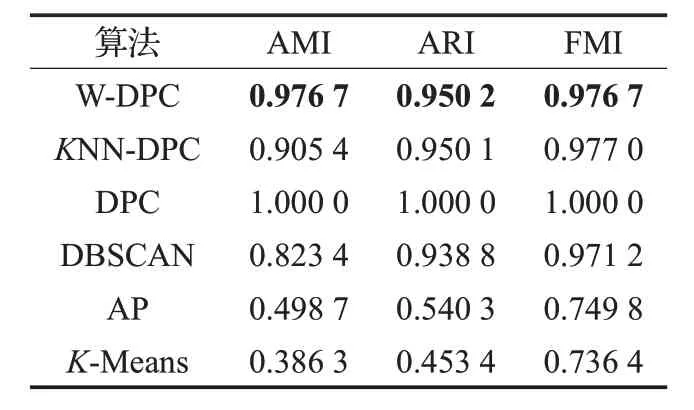
表2 Flame数据集上的聚类结果比较
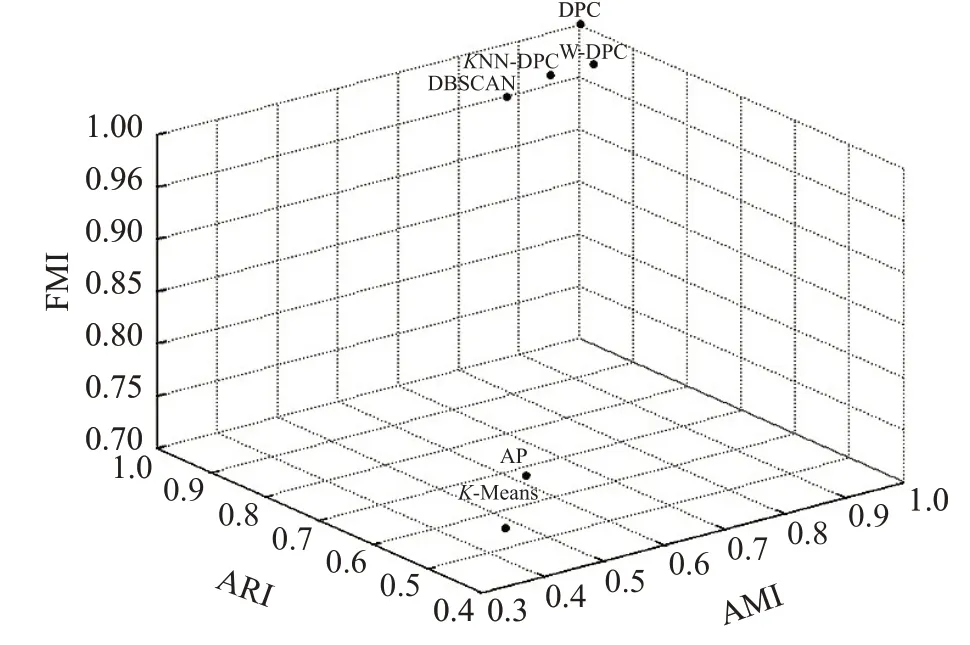
图3 表2中的三种评价指标散点图
为了进一步验证W-DPC算法的性能,Spiral People数据集上聚类的效果图以及评价指标如图4所示。
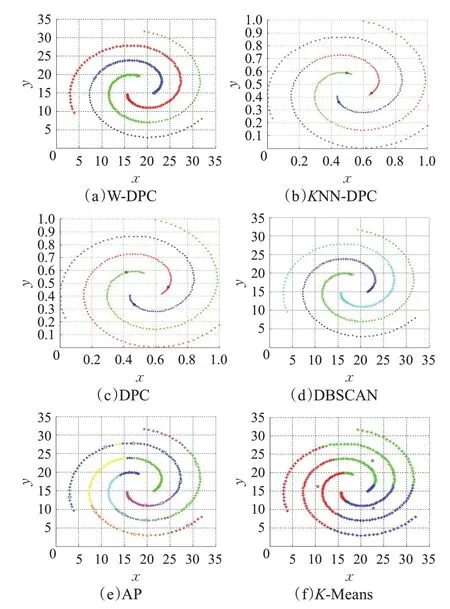
图4 六种算法在Spiral数据集上的聚类效果图
从表 3 中可以看到,KNN-DPC 算法、DPC 算法、DBSCAN算法的AMI、ARI、FMI都达到了100%;图4中这三种算法将该数据集分成正确的类簇数目、能够准确识别质心并且剩余数据点的分配也很精准,聚类效果较好;AP算法将该数据集分成多个类簇,识别出多个类簇中心,进而使得部分样本点分配到错误的类簇中,影响最终的聚类效果;K-Means算法将数据集分成了正确的类簇数目,但是类簇质心识别的差异较大,导致剩余样本中本该属于同一类簇的却被错误的分配到多个类簇中,其AMI、ARI达到负数,超出这两种评价指标的取值范围。从图4、表3、图5 可以看出W-DPC 算法对Spiral数据集聚类效果更优,AMI、ARI、FMI 都达到了100%,高于AP 算法70%左右,更高于K-Means 算法,W-DPC算法将Spiral数据集聚类成正确的类簇数目,精准识别质心位置及分配剩余样本点。
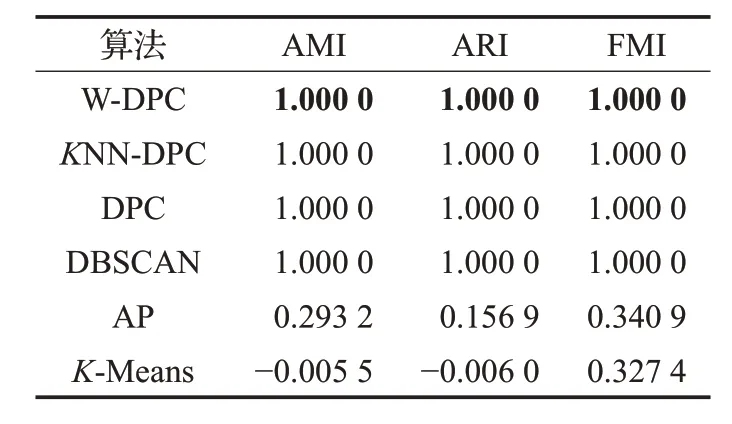
表3 Spiral数据集上聚类结果的比较
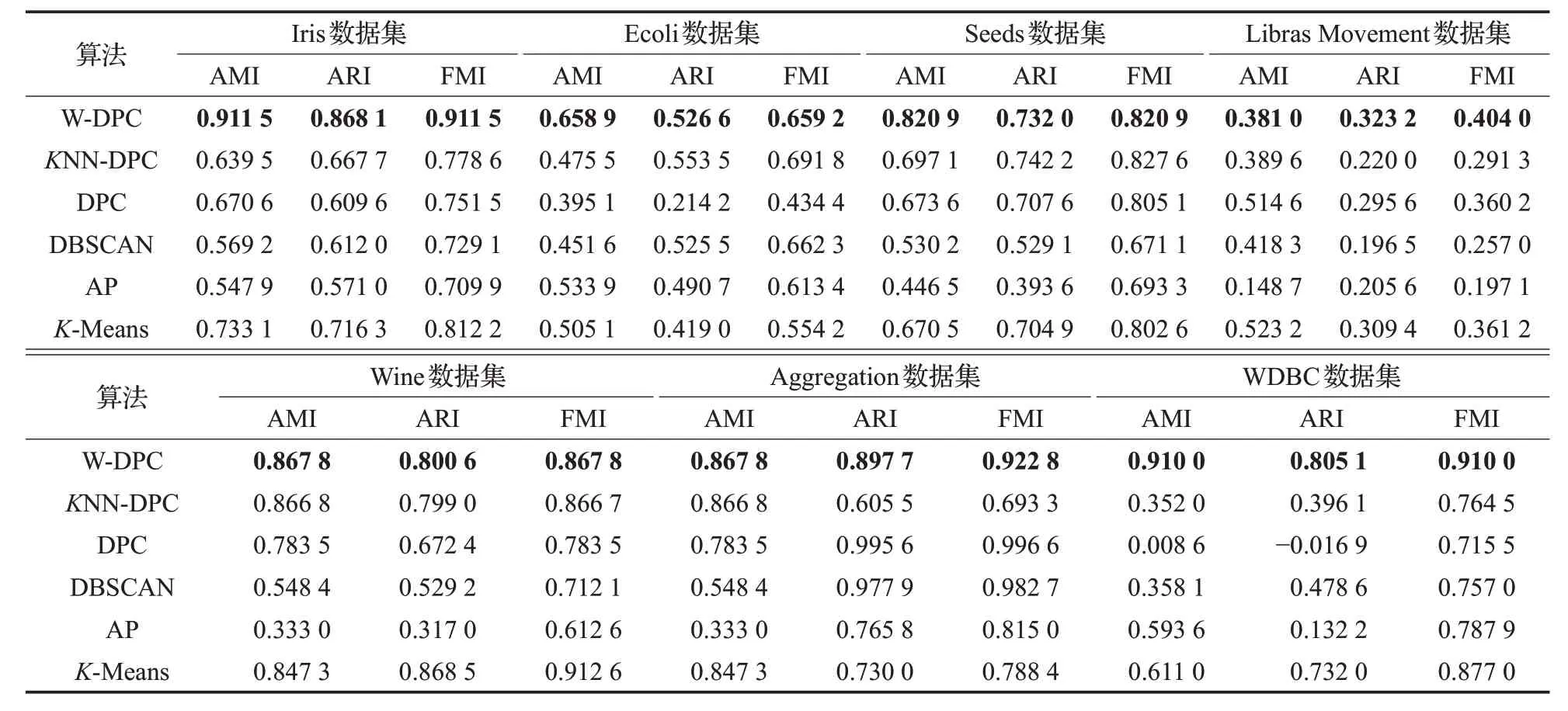
表4 W-DPC与其他算法在七个数据集上的聚类结果比较
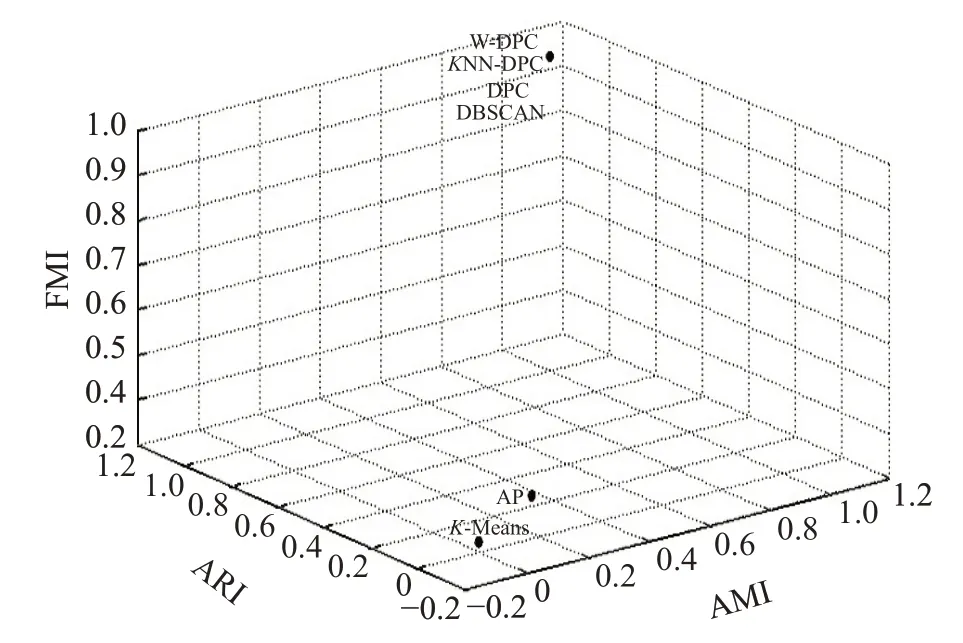
图5 表3中的三种评价指标散点图
本文选取UCI上的七个真实数据集对W-DPC算法以及其他算法进行实验,实验结果如表4所示。
从表4中可以看出,W-DPC算法的聚类性能要明显优于其余的几种聚类算法。
W-DPC算法几乎对所有的数据集都具有更优的聚类效果,对于类簇数目及其质心的识别更加准确;对于FMI 以及互信息AMI,W-DPC 算法的这两项指标均高于其余算法10%~20%,对于数据集中局部密度的计算更加高效,使得样本之间的密度差异性更明显,W-DPC算法所产生的聚类结果与原始数据集之间的相似度更高,整体上来看,W-DPC 算法的各项评价指标系数较高,且该算法性能较为稳定。
从上述理论分析和实验评估可以得出结论:与其他算法相比,W-DPC 算法的聚类表现最好,平均性能稳定,所定义的局部密度使得样本之间密度差异性增大,有利于识别高密度的样本;两步分配策略更有助于实现样本自发的聚合与离散。
表5显示表1所提供数据集平均的运行时间。为了降低结果对意外事件的敏感性,对于每个数据集,应用最佳参数并执行相同的过程50次。由于只有W-DPC算法、KNN-DPC 算法和传统的DPC 算法是在matlab2017中实现的,因而表格省略了其他算法的运行时间。
由表5 可知,W-DPC 算法的运行时间大约是DPC算法的7倍左右,但是根据表4可以看出W-DPC算法的聚类精度要远远高于DPC算法。
5 结束语
本文针对DPC 算法存在的问题,从局部密度和分配策略这两个方面进行了改进:
(2)根据第一宇宙速度来改进分配策略,将所有的剩余样本点根据必然从属于和可能从属于某个类簇进行划分,避免了一步分配策略导致的容错性等问题。

