考虑箱区作业均衡的ACT船舶配载鲁棒优化研究
丁 一,田 亮,龚 杰
上海海事大学 物流研究中心,上海 201306
1 引言
近年来,随着经济的发展,科技的进步以及传统集装箱码头相较于自动化码头在人力成本、人员安全和作业效率等方面的劣势,诸如上海洋山四期等自动化集装箱码头相继建成并投入运营。自动化集装箱码头(Automatic Container Terminal,ACT)高效作业的重要原因在于持续的智能化无人作业以及多决策系统模块的集成,配载就是集中系统中的一个关键环节。集装箱码头的配载业务是按船舶的运输要求和码头的作业要求,编制预定装载于既定船舶箱位的装载计划[1],配载质量的高低直接影响到船舶航行安全以及码头装船作业效率与成本,因此码头必须在考虑船舶的航行安全与盈利的条件下,充分考虑在场箱堆存情况与作业工艺的情况,以确定最佳配载方案,提高装船作业效率,减少装卸作业成本。自动化码头堆场与传统码头堆场的布局与机械配置如图1所示,堆场布局与机械配载方面的差异导致作业工艺的不同,也直接影响着配载的考虑因素。

图1 集装箱码头堆场布局图
在传统集装箱码头堆场中,堆场箱区平行于码头岸线布置,箱区龙门吊大多使用的是轮胎吊(Rubber-Tyred Gantry Crane,RTG),RTG 的运行轨迹平行于码头岸线,可以跨箱区作业,因此RTG与内外集卡的交互点不固定,而在ACT 堆场中,堆场箱区垂直于码头岸线,箱区龙门吊大多使用轨道吊(Rail-Mounted Gantry Crane,RMG),RMG 的运行轨迹也垂直于码头岸线,相邻箱区之间没有作业区域(设有悬臂吊的箱区除外),只设有海侧和陆侧交换区作为RMG与外集卡和自动导引车(Automated Guided Vehicle,AGV)的交互点,因此收发箱点固定,属于单侧作业模式,如果同一时间内部分ACT箱区装卸量偏小,而部分ACT箱区装卸量偏大,即作业不均衡,而单位时间内RMG的作业能力有限,一旦某个箱区的发箱指令过于集中,就会造成某一段时间内该箱区作业量过大,易产生RMG 作业冲突,会造成AGV 和岸桥(Quay Crane,QC)的等待时间增加,从而影响港口作业效率,延长总装船时间,进而延误船期,因此发箱时考虑箱区之间的作业均衡至关重要。
目前,学者们主要从两个视角对船舶配载问题进行研究,一是从船公司的视角,另一种是从码头视角。从船公司的角度,主要解决的问题是如何减少装卸箱时由于多装货港与多卸货港货物的存在导致的倒箱,其次是考虑船舶的航行安全,如Delgado等[2]考虑20′/40′箱的混装、冷藏箱等特种箱的配载以及船舶积载强度等因素,以最小化倒箱为目标,建立解决集装箱船舶配载中的倍位计划(master planning)子问题的整数规划模型与解决箱配(slot planning)子问题的约束规划模型,并证明约束规划在求解此类问题中的有效性;而Parreño等[3]在Delgado等[2]的基础上,以最小化漏配箱数、倒箱为目标,建立新的整数规划模型,并设计GRASP方法,重点解决配载的箱位分配子问题。在追加考虑船舶稳性的因素后,Ambrosino 等[4]将单卸货港倍位计划问题延伸到多卸货港倍位计划问题,以最小化靠泊时间为目标,设计求解问题的MIP 启发式方法;而Pacino 等[5]则以同样的目标,分别建立倍位计划问题的整数规划模型和单个集装箱的箱位问题的约束规划模型,Ding等[6]则将目标换成最小化倒箱;汪圆圆等[7]在保证倒箱量为零的策略下,以船舶中纵剖面弯矩值、重心横向偏移、初稳性高为目标,以船舶吃水差值为约束条件,优化集装箱配载;孙俊清等[8]将船舶稳定性作为约束条件,以最小化集装箱船舶在整个航线所有港口的倒箱量为目标,设计了求解问题的改进遗传算法。
而从码头的角度,解决的问题主要是确保配载结果足以保证船舶航行安全,此外尽量缩短装船作业时间,如Araújo等[9]将三维集装箱船舶装船计划问题(3D-CLPP)的目标定为最小化船上的倒箱和最大化船舶的稳定性;Monaco 等[10]在预配规则已定的条件下,建立配载问题0-1整数规划模型以优化码头的堆场翻箱时间与集装箱水平运输时间,但没有考虑堆场作业不均衡造成的作业等待。在满足船舶配载计划的前提下,祝慧灵等[11]以堆场翻箱量最小为目标分别建立3 种翻箱策略下的提箱顺序优化模型;在增加最小化船舶贝内翻倒箱数量及横倾力矩的目标后,李俊等[12]构建集装箱船舶装箱排序问题的数学模型并设计SWO-HES 两阶段算法对问题进行求解。
通过对文献的系统梳理可以发现,目前学者们在研究集装箱船舶配载问题时,大多从船公司角度出发,较少从码头角度出发,所考虑的因素主要有以下几点:(1)“重不压轻”、“远不压近”约束,即重箱在下,轻箱在上,远卸货港箱在下,近卸货港箱在上;(2)偶数倍位集装箱箱槽内20′与40′箱的混装约束(甲板或舱内的同倍位同排位不同层位的所有箱位同属一根箱槽);(3)特种箱的配载约束;(4)吃水差、稳性和船体强度约束等。鉴于ACT 箱区单侧作业的特殊性以及对装船效率的要求,仅考虑以上这些常规约束制定出的配载方案已满足不了ACT 实际生产需要,引入ACT 箱区作业均衡性就显得尤为重要。但目前以ACT 为背景的配载研究较少,缺乏ACT 箱区的作业均衡对配载装船作业影响的研究。此外,在实际装船过程中,存在众多不确定因素,如QC作业时间、AGV水平运输时间、RMG堆场作业时间、集装箱未按规定时间顺利进场等,这些不确定性直接影响着配载方案的可行性与满意度。在目前的配载研究中,所有的参数都是确定的,缺乏不确定性对配载结果影响的研究。
2 问题描述
集装箱船舶配载[13]是指:码头根据作业规定和船舶安全航运要求,制定出满足船舶最基本稳定性要求,尽可能减少翻箱次数,缩短装船时间,降低营运成本的船舶装载计划。从根本上来说,船舶配载问题可以划分为两个子问题:(1)“When”问题,即在场箱何时离场,也即装船作业顺序(loading sequence)问题。船舶箱槽(船上同倍位同排位不同层位的船箱位所属同一根槽)中一定是下层箱位先装箱,如果将同一堆栈(同箱区同倍位同排位不同层位的集装箱所属同一堆栈)的下层箱子配于船舶同一根槽的上层箱位,则装船时就需要将同一堆栈的上层箱子移走才能取出下层箱子装船,堆场翻箱操作由此产生。做配载时,待装船的在场箱的场箱位是已知的,是否翻箱或有多少翻箱完全取决于配载的结果,即配载船图。“When”问题的结果就是最优的装船作业顺序。(2)“Where”问题,确定该箱离场后被安排在哪一船箱位,“Where”问题的结果就是配载的贝位船图。
船舶配载的一个重要目标在于减少船舶在港装卸时间,因此在给定船舶预配船图、桥吊作业计划(Crane Working Planning,CWP)和在场箱信息后,考虑常规配载约束和箱区单位时间作业量约束,以最小化总装船时间和同时段内箱区最大与最小作业量的差额(即箱区作业均衡)为目标,建立混合整数规划模型。在上述确定性优化模型的基础上,考虑到桥吊作业时间的不确定性对配载的影响最为直接,将桥吊作业时间改为不确定参数,建立考虑桥吊作业时间不确定性的ACT 船舶配载鲁棒优化模型,通过基于编号与排序的禁忌搜素算法得到最优的配载方案,保证该配载方案能够使得装船作业过程中的箱区作业均衡,并且对桥吊作业时间的不确定具有较强的鲁棒性。
3 确定性模型建立
3.1 参数
N:所有待装船的在场集装箱的集合,i=1,2,…,|N|,∀i∈N;
B:所有待装船的在场集装箱所在堆场箱区(Block)的集合,b=1,2,…,|B|,∀b∈B;
P:船上待装集装箱的箱位(Slot)集合,p=1,2,…,|P|,∀p∈P;
T:作业总时间内分钟段集合,t=1,2,…,|T|,∀t∈T,如t=3 表示第3分钟内;
H:作业总时间内小时段集合,h=1,2,…,|H|,|H|=ceil(|T|/60),表示取大于等于|T|/60 的最小整数值,则t=[1+60(h-1),60+60(h-1)],∀h∈H,如h=3 表示第3h内;
qb:每一小时段内箱区b的最大集装箱作业量;
fb:箱区b内待装船的集装箱总数;
wi:集装箱i的重量,其中 ∀i∈N;
θp:箱位p的开始装箱时间,其中∀p∈P;
τip:集装箱i从其所在的堆场箱区到最终的箱位p所对应的船舶倍位的水平运输时间,其中∀i∈N,p∈P;
L:表示船上根据预配载计划所形成的集装箱箱槽的集合,;
Ψl:属于船上箱槽l中的箱位,∀l∈L,Ψl∈P;
Wl:船上箱槽l所能容许的最大装箱总重量,∀l∈L;
Δi:表示与集装箱i在同一箱区同一堆栈且位于i之上的集装箱的集合,Δi⊂N,∀i∈N;
πp:表示与船舶箱位p在同一根箱槽且位于p之上的箱位的集合,πp⊂P,∀p∈P;
σ1:箱区内的一次翻箱时间;
σ2:对不均衡可能导致的等待的惩罚时间。
IFIP:是一个二维|N|*|P|的0-1 矩阵,表示 |N|个待装船在场箱中的i是否符合预配总图关于该箱位的类型、尺寸、卸货港的要求从而装到|P|个计划船箱位中的p,如果可以,则矩阵对应元素IFIPip=1,否则为0。如果IFIPip=0,则说明按预配计划,i不可以装到p箱位,那么xipt=0,因此有关系式:xipt≤IFIPip;
IFIB:是一个二维|N|*|B|的0-1 矩阵,如果在场箱i位于箱区b,则矩阵对应元素IFIBib=1,否则为0。
TIP:是一个二维|N|*|P|的整数矩阵,表示如果在场箱i被安排到船箱位中的p,那么该集装箱应该离场的时间TIPip=θp-τip;
λ1,λ2:权重系数;
M:一个极大正数。
3.2 决策变量
xipt:代表集装箱i在t时间从箱区离场,并且被安排到船箱位p;
zij:0-1变量,当集装箱i先于j离场时取1,否则为0,其中
Ωh:第h小时各箱区出箱量的最小值;
Rh:第h小时各箱区出箱量的最大值。
3.3 假设条件
(1)当前待配载船舶只有一条船,且不考虑边装边卸。
(2)考虑到冷藏箱和危险品箱一般有配载员直接指定配载位置,本文仅考虑普通箱的配载。
(3)只考虑装船情况,假设到港后进口箱均已卸载。
(4)码头一般根据进、出口箱和码头自身情况,配置一定数量的集装箱岸桥,本文假设已事先获得各港口可分配的岸桥类型和数量。
(5)在计算箱区翻箱量时,只考虑单条船舶装船作业时堆场的翻箱,不考虑因多船舶同时装船造成的翻箱。
(6)预配船图一经船方确定,不会发生变化。
3.4 完整模型
其中,目标函数:
(1)最小化总装船时间:

(2)最小化各箱区作业量的不均衡程度:

为了便于计算,可将目标函数(2)线性化,定义:

由此,式(2)转化为式(5):

问题描述中,箱区作业量的不均衡程度较大时可能会造成装船作业时的等待时间,因此为了减少等待的发生,给不均衡的箱量以一定的惩罚时间σ2,另外引入权重系数λ1、λ2,将多目标函数转化为单目标函数:
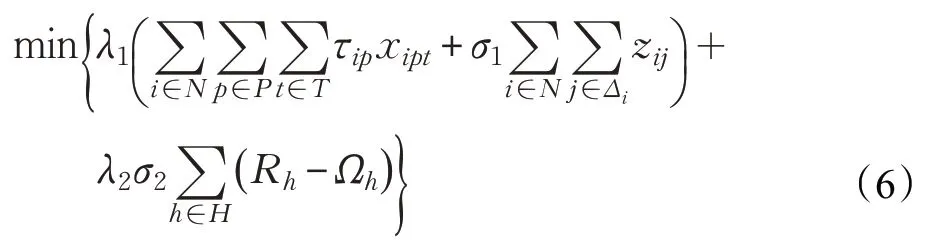
可得完整的考虑箱区作业均衡的ACT船舶配载混合整数规划模型如下:

s.t.


公式(7)表示目标函数,最小化实配过程的集装箱装船作业时间和最小化不同箱区作业量的不均衡程度。式(8)和(9)为匹配约束,即一个集装箱只能被安排到一个船箱位中,而一个箱位也只能放一个集装箱。式(10)表示集装箱与船箱位的匹配需要满足预配要求。式(11)表示在场箱离场须符合CWP作业时间安排。式(12)为轻压重约束,即船上同一根箱槽的集装箱,重箱一定位于轻箱的下层。式(13)为船舶单根箱槽的装载重量约束,规定每一根箱槽堆码的总重量不允许超过设定的最大值。式(14)和(15)为箱区作业约束,式(14)表示同一时间段内从该箱区离场的最大集装箱数量。式(15)表示从堆场一箱区离场的集装箱总数量。式(16)表示在场箱离场先后顺序与翻箱的关系。式(17)和(18)用来求取每一时间段内各箱区作业量的最小值和最大值,同目标函数一起达成箱区作业均衡的目标。式(19)表示决策变量类型。
4 鲁棒性优化模型
4.1 鲁棒优化方法
根据不确定性变量建模方法的不同,不确定性优化方法一般可分为三类:随机规划、模糊规划及鲁棒优化[14]。鲁棒优化[15]是一种解决不确定性问题强有力的工具,其通过“集合”的形式描述变量的不确定性(而不是通过概率分布),使得约束条件在不确定变量取值于已知集合中所有可能值时都能够满足,并以此建立最极端情况下优化目标函数的鲁棒对等模型。该方法的优点是:(1)决策者能够调节解的鲁棒水平;(2)鲁棒模型可以转化成线性规划,易于求解;(3)能够求出鲁棒解满足约束条件的概率下界。因此本文应用Bertsimas 和Sim[16]提出的鲁棒方法,采用“盒子”作为不确定时间的集合,并引入保守性参数,提出桥吊作业时间不确定的考虑箱区作业均衡的ACT 船舶配载鲁棒优化模型,再应用强对偶定理,将非凸非线性的鲁棒模型转化为线性规划。
4.2 鲁棒优化模型
确定性模型中,桥吊作业时间是确定的,这里将桥吊作业每关箱子的时间作为一个不确定参数处理,引入如下参数。
gp:箱位p的作业关号,∀p∈P;
θp:箱位p的开始装箱时间(CWP预计值,名义值);
ξp:箱位p的开始装箱时间,为一个不确定值,其中∀p∈P,假设ξp取值于有界的对称区间上,也称为“盒式”集合,为最大时间偏差(定值),ρ为偏差系数,ρ∈[-1,1] 。
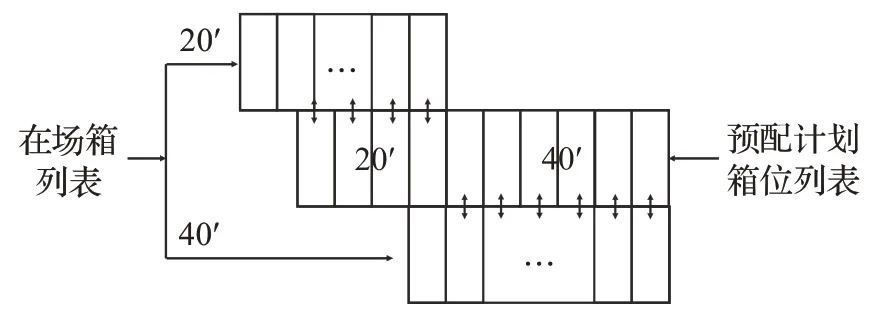
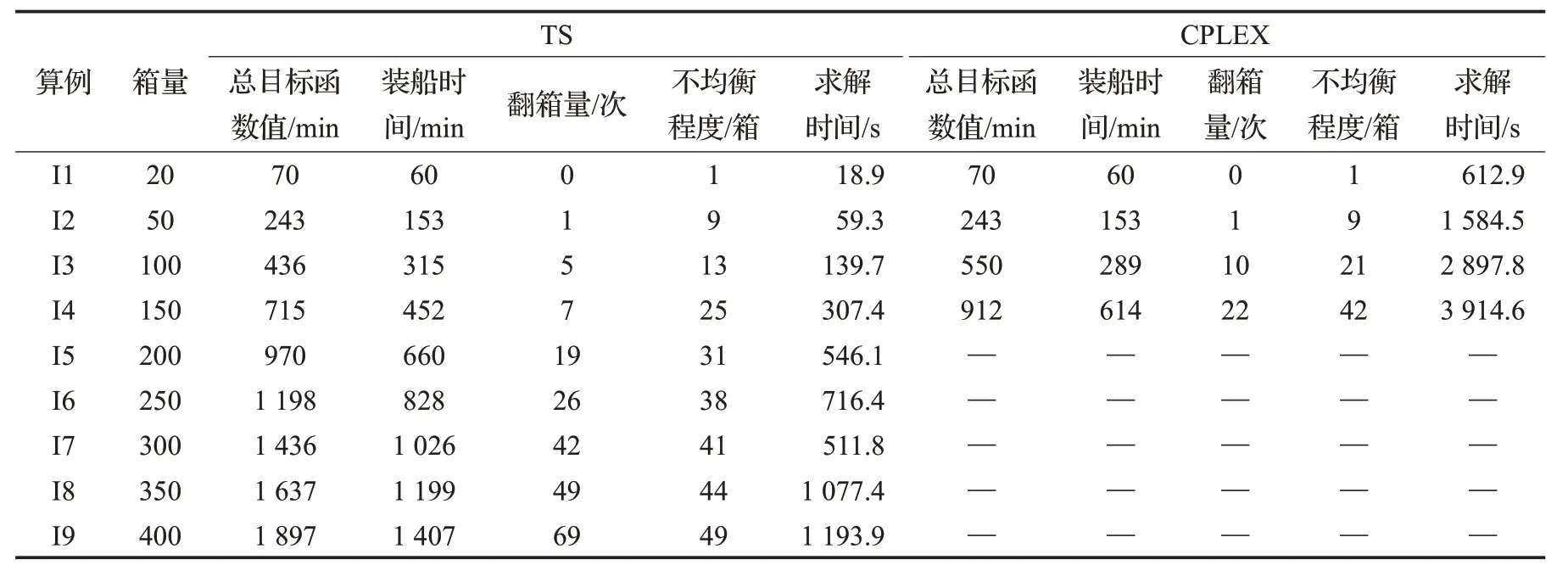
根据CWP,按计划作业开始时间的先后(计划关号)对箱位进行编号(递增),考虑到桥吊作业时间的不确定性将直接影响后续箱位的开始装船时间,因此为简化相关关系,将桥吊作业的不确定性转移到箱位的开始作业时间上去,有如下关系:fgp 本文应用Bertsimas和Sim[16]提出的鲁棒方法,在约束(16)中,对 ∀i∈N,j∈Δi,引入一个参数Γij,Γij不一定是整数,取值在区间[0,|P|],参数Γij的作用是调节鲁棒水平,控制解的保守性。直观地讲,不是所有的ξp都会变动,该鲁棒方法的目标是当最多有个ξp在其区间内发生变化时鲁棒解仍是可行解,不失一般性,Γij的取值越高,决策的风险性越低,但代价也越大。 由于约束(16)含有不确定参数ξp(ξp),且决策变量xipt为0-1变量,可将约束(16)转化为: 其中: 此时,当 时,必有zij=1。 如果: 时,只有当 时,才有zij=1。 当Γij的取值不是整数时,表示有个ξp在其区间内发生变化,一个ξp的取值扰动为当Γij的取值是整数时: 引入辅助变量zp,∀p∈P,则函数g(x,Γij)可表示为: 式(23)是一个线性规划问题,若给定x* ,可用Cplex求解器进行求解。当Γij=0时,此时最多有0个ξp同时偏离均值,即所有ξp都取均值,此时约束(20)与约束(16)相同,鲁棒问题转为确定问题,当=Γij=|P|时,此时最多有|P|个ξp同时偏离均值,也就是所有ξp都取最大值,此时约束(20)变为: 即当Γij=|P|时,该鲁棒方法转化为Ben-Tal和El-Ghaoui[17]提出的鲁棒方法,即考虑ξp都取最大值的情景,虽然该方法求得的解在ξp的任何变动下均为可行解,但是会对目标函数值造成较大的影响,显然,此时得到的解过于保守。而应用Bertsimas和Sim[16]提出的鲁棒方法,决策者可以通过控制Γij的值,调节解的鲁棒性来避免对目标函数值造成较大的影响。通过引入辅助参数ωij和rp,由线性规划的强对偶理论将约束(20)转化为如下鲁棒线性对应式: 此外,约束(11)中也含有唯一的不确定性因素ξp,考虑到在场箱离场时间与ξp的实际关系,这里根据Soyster[18]提出的方法将约束(11)转化为: 由以上的转换可得,自动化集装箱码头船舶配载鲁棒优化模型为: s.t.(8)~(10),(12)~(15),(17)~(19),(25)~(29) 本文所研究的集装箱船舶配载问题是一个多目标多约束的组合优化问题,属于NP-hard问题[19-20],当问题的规模较小时,尚且可以使用Cplex求解器利用精确算法求得最优解,但当问题的规模较大,且决策变量维度较多时,欲求准确的最优解已基本不可能,并且船舶大型化使得配载问题更加复杂。因此从满足实际应用的角度出发,本文基于配载问题自身的特点设计了基于编号与排序的禁忌搜索算法。 禁忌搜索算法(Tabu Search,TS)由美国科罗拉多大学系统科学家Glover[21]教授于1986 年首次提出,是一种扩展邻域的启发式搜索办法,是对人工智能的一种模拟,用于求解大规模组合优化问题的有效算法。该算法能以较大概率跳出局部最优点,通过引入一个灵活的存储结构和相应的禁忌准则来避免迂回搜索,并通过藐视准则来挽回一些被禁忌的优良状态,进而保证多样化的有效搜索以最终实现全局优化。禁忌搜索涉及到邻域结构(neighborhood)、禁忌表(tabu list)、禁忌长度(tabu length)、候选解(candidate)、藐视准则(aspiration criterion)、禁忌对象和终止准则等环节。 配载所需数据包括在场箱信息、预配船图及CWP等,对配载所需数据进行详细梳理,如图2 所示,这样,“i”行的集装箱与“p”行的船箱位一一对应,就可以用来表示计划配载的结果,因此解的形式如式(31)所示: 因为在场箱离场时间与桥吊开始作业时间直接相关,并且翻箱量与箱-位安排即配载直接相关,因此确定了这样的x,也就确定了模型中的决策变量xipt与zij。 下面说明禁忌搜索的重要参数设计。 图2 解的形式与数据结构示意 (1)初始解 TS对于初始解具有较强的依赖性,较好的初始解可使TS在解空间中搜索到更好的解,为了获得一个较好初始解,如图3所示,首先对预配计划箱位根据预配规则进行编号和排序(按卸货港、箱位尺寸进行升序排序,对于同一卸货港和箱位尺寸的箱位再根据倍位、层位和排位进行升序排序)形成预配计划箱位列表,再对在场箱进行编号和排序(先根据卸货港、箱位尺寸进行升序排序,对于同一卸货港和箱位尺寸的集装箱再根据集装箱重量进行降序排序)形成在场箱列表,若在场箱(20′与40′箱)多于预配计划箱,以20′箱为例,将在场箱列表中的最后一个集装箱与预配计划箱位列表中的最后一个箱位对应,以此向前截取连续的在场箱列表,满足与预配计划箱位列表全部箱位一一对应,40′箱同样操作,这样所有船箱位都安排了在场箱,构成一个基本解xr。 图3 初始解的获得 在得到一个基本解xr(以及后续解的交换)后,需要验证其可行性,考虑到所有约束以及不确定性参数对配载结果的影响,在此作如下定义: 以上参数代表分别代表对相应约束的违背程度,其中ν(αij(xr),βp(xr),γbh(xr))表示所有约束的总违背程度,如果ν(αij(xr),βp(xr),γbh(xr))=0,则可认为xr满足所有约束,为一个初始可行解F。如果ν(αij(xr),βp(xr),γbh(xr))≠0,则将xr的评价函数eval(x)定义为如下: 其中,f(x)为实际目标函数值。若选择合适的惩罚函数penalty(x),则无论不可行解的实际目标函数值如何,都不会选为最优解。 (2)邻域结构 采用随机混合邻域结构。轮盘赌选择一种邻域交换方法,获得新的解,在迭代过程中每次都随机选用其中的一种。 ①交换算子M1(xr,i,j) 在配载方案xr中,若任意的两倍位Bayi与Bayj之间具有同类属性的箱子,选择Bayi与Bayj中同类数量少的箱组按照原先的轻压重进行两倍位间的整体转移交换。 ②交换算子M2(xr,i,j) 在配载方案xr中,若同类同贝的多个层中的箱子都可以交换,则随机选择一层中可交换的i和j进行交换。 ③交换算子M3(xr,i,j) 在配载方案xr中,若同类同贝的多个层中的箱子都可以交换,则将所有层中可交换的i和j进行交换。 交换后的解仍然满足预配和轻压重约束,通过交换即可产生一个邻域解,由i到i′的交换示意如图4所示。 图4 解的交换示意图 (3)候选解集 在当前状态的邻域解集中选取一定数量的较优解构成候选解集CandidateSet。 (4)评价函数 取模型目标函数作为评价函数,其中不可行解的评价函数包括惩罚函数penalty(x)。 (5)禁忌对象 为了获得较大搜索范围,选择解的简单变化,即箱-位的一个全排列作为禁忌对象。 (6)禁忌长度 将禁忌长度设为一个常数TabuLength。 (7)藐视准则 选择基于适配值的准则作为藐视准则。 (8)终止准则 最后设定最大迭代步数为一个常数MaxIterNum,同时,若在一定迭代次数(Maxfreq)内当前最优解无优化趋势,则提前跳出搜索过程。 以初始基本解即当前初始箱-位匹配为例。首先设置模型与算法参数,假设算例中集装箱数为Container-Num,则确定算法的最大迭代次数MaxIterNum,禁忌长度TabuLength,候选解个数CandidateNum,候选解集CandidateSet为空,最后设定空禁忌表TL,具体的迭代步骤如下: 步骤1 输入初始基本解xb,置当前迭代次数d=1,当前最优解无优化迭代次数freq=0,进入步骤2。 步骤2 判断xb是否满足船舶箱槽重量约束和箱区作业约束,是则进入步骤4,否则进入步骤3(Swap)。 步骤3 随机选择一种交换算子,进入步骤3.1。 步骤3.1 若选择交换算子M1,根据交换规则进行交换,进入步骤4;否则,进入步骤3.2。 步骤3.2 若选择交换算子M2,根据交换规则进行交换,进入步骤4;否则,进入步骤3.3。 步骤3.3 若选择交换算子M2,根据交换规则进行交换,进入步骤4。 步骤4 置初始解x0=xb,当前解x=xb,当前最优解BSF=x0,计算当前最优解对应的最优值BV=GetValue(BSF),FreqValue=BV,进入步骤5。 步骤5 判断当前d是否小于MaxIterNum,是,多次执行步骤3(Swap),将得到的可行邻域解置于CandidateSet中,直至CandidateSet中的候选解数目达到CandidateNum,计算各候选解的目标值V=GetValue(each xinCandidateSet),进入步骤7;否则,进入步骤6。 步骤6 返回BSF、BV,记录当前箱位匹配对应的最优配载方案及其对应的目标函数值,再将在场箱列表中的倒数第二个集装箱与预配计划箱位列表中的最后一个箱位对应(箱-位平滑移动匹配,如图5所示),以此向前截取连续的在场箱列表,满足与预配计划箱位列表的全部箱位一一对应,返回步骤1,直至在场箱列表中的第一个集装箱与预配计划箱位列表中的最后一个箱位对应,选择一个目标函数值最小的配载方案作为最终的最优配载方案,算法结束。 图5 箱-位平滑移动匹配 步骤7 判断min(V)是否小于BV,是,令BSF=x,x置于TL中,更新TL;否则,将x置为邻域中非禁忌的最优x,x置于TL中,更新TL,进入步骤8。 步骤8 判断FreqValue是否小于等于BV,是则freq=freq+1,进入步骤 9;否则,FreqValue=BV,freq=0,进入步骤10。 步骤9 判断freq是否大于等于Maxfreq,是则返回步骤6;否则,进入步骤10。 步骤10d=d+1,返回步骤5。 将上海洋山港区某集装箱码头配载所需的数据分为9 组,生成规模大小不同的9 个算例I1~I9,算例数据如表1所示。其中,箱量表示该算例中的在场箱总箱数(预配箱数等于在场箱数),卸货港数表示该算例中的在场箱分别属于几个卸货港,T堆栈数表示该算例中的在场箱中,一堆只有1 个集装箱的堆栈数,2T、3T和4T以此类推。 根据该码头的实际作业情况确定模型中的部分参数,其中,箱区单位小时的最大作业箱量qb=15 箱,箱位p的开始装箱时间由已知的CWP确定,鉴于ACT在场箱分布相对分散,取集装箱i从其所在的堆场箱区到最终的箱位p所对应的船舶倍位的水平运输时间τip=3 min,箱区内一次翻箱时间σ1=3 min,箱区不均衡程度较小时不一定导致作业等待,但是不均衡程度较大时很有可能造成等待,因此综合考虑,取不均衡可能导致的等待的惩罚时间σ2=2 min,模型参数确定后,在MatLab R2016b中利用算法对模型进行求解。实验使用的电脑配置为Win7 64位操作系统,4 GB运行内存,处理器为Inter®Core™ i5-320M,CPU频率为2.6 GHz。算法的相关参数定义:候选解个数CandidateNum=50,禁忌长度TabuLength取大于ContainerNum0.5的最小整数,算法迭代的最大次数MaxIterNum=200,允许当前最优解无优化趋势的最大迭代次数Maxfreq=50。 表1 算例数据说明 对于每个算例,同时取不均衡可能导致的等待的惩罚时间σ2=0,即不考虑箱区作业均衡因素对配载结果的影响,在得出各案例最优配载方案后,计算各配载方案的箱区作业不均衡程度(箱),与σ2=2 min 时的结果进行比较,分析箱区作业均衡因素对配载结果的影响。在参数k=λ1∶λ2=1∶10的情况下,计算结果如表2和表3所示。 由表2 可以看出,9 个算例中,禁忌算法都能够在21~1 200 s 的时间之内求解出结果,而Cplex 只能解决箱量为20、50、100、150箱的案例,但求解质量较差由此可见Cplex在求解复杂的大规模配载问题时效率较差,相比之下,本文算法对求解大规模集装箱码头配载问题有着很好的求解效果和求解效率。 表2 算例结果 表3 均衡因素对配载结果的影响 由表3可以看出,各案例在不考虑箱区作业均衡因素时得到的箱区作业不均衡箱量比考虑箱区作业均衡因素时得到的箱区作业不均衡箱量分别高出0%,0%,23.1%,20.0%,22.6%,8.3%,29.3%,34.1%和22.4%,平均高出17.8%。高出的不均衡箱量势必影响船舶装船作业效率,因此在自动化集装箱码头配载时亟需考虑箱区作业均衡因素。 完整的船舶配载计划由在场箱装船作业顺序以及合理的倍位船图构成,在场箱装船作业顺序已由CWP确定,因此图6 展示了集装箱、船箱位与场箱位的对应关系(该配载结果取自算例I9),其中船舶53 倍位的这些集装箱分别来自第10 箱区57 倍位、50 箱区29 倍位、56箱区43倍位、64箱区23倍位和72箱区65倍位,如位于 64 箱区 23 倍位 5 排 1 层的在场箱 CAIU6122728 被安排在了船上53倍位08排04层的箱位。 图6 集装箱、船箱位与场箱位的对应关系 依然选择前一节的数据进行算例分析,并选择该船的17 舱66 倍位中的出口箱为例。预配船图如图7 所示。该码头的所有在场箱堆存信息已知,包括集装箱号、尺寸、箱重、卸货港、场箱位(箱区、倍位、排位和层位),共涉及147个在场待装集装箱。需要说明的是,在17 舱 66 倍位中,计划配载箱位数为 90 个 40′箱,而满足该倍位的卸货港配载要求的在场箱共有147个40′箱,通过平滑移动的方法选取90个在场箱并安排到预配箱位中,完成配载方案。 为了分析鲁棒水平对配载方案和目标函数中各项指标的值的影响,分别对Γij取[0,90]中间隔为10 的不同值,同时部分参数取值如下:k=λ1∶λ2=1∶1 ,σ1=3,,得到的结果如表4所示。 从表4可以看出,随着Γij取值的不断增大,相比于总目标函数值,表明随着保守系数Γij取值的增大,虽然求得的解在部分桥吊作业时间在其取值区间任意变化时,均为可行解,但是会对目标函数造成较大的影响。总装船时间与不均衡程度,翻箱量也呈现大幅增长的趋势,当=Γij=|P|=90 时的翻箱量已经比Γij=0 的翻箱量多出了2 000%,主要原因如下: 图7 17舱位66倍位预配船图 表4 鲁棒水平(Γij 值)对目标函数中各项指标值的影响 显然此时的解过于保守,因此,决策者可以通过选择合适的Γij的值来应对桥吊作业时间的不确定性,同时获得一个比较满意的配载方案。另一方面,鲁棒模型旨在获得一个更优的鲁棒解,在保证解有较好鲁棒性的同时,也会对配载方案的决策产生重要影响。表5是确定(Γij=0)与不确定情况下,17舱66倍位的集装箱的来源堆场场地的对比。 表5 确定与不确定情况下集装箱来源场地的对比 从表5 可以看出,不确定性情况下,算法更倾向于“集中配载”(其中箱区A2、A4与B4 这种集中效果最为显著),即用尽可能少的箱区和箱区倍位满足船舶倍位的配箱要求,因此将同一堆场甚至是同一倍位的在场箱配于船上同一倍位,这种“集中配载”之所以能够使配载方案更优,原因可由图8进行说明。 图8 中,“()”里的数字表示该箱位的作业关号,a、b、c、d为4个集装箱,4个集装箱装船前的箱区堆存情况以及实配船图如图所示,例如位于箱区第4层的集装箱a 配载到船上2 倍位04 排02 层的位置,且作业关号为5。在确定情况下,2倍(1)(2)(3)(4)按计划时间与顺序完成装箱,2倍(5)(6)开始时间早于10倍(3)(4)开始时间,这样配载没有翻箱出现。但是当2倍(1)(2)(3)(4)的作业时间不确定时,假设作业时间过长导致后续装箱开始时间延迟,进而导致10倍(3)(4)先做装船作业,则c、d装船时就需要翻箱。 图8 假设确定性情况下两倍位的配载结果 如果把a、b、c、d配在同一船舶倍位里,甚至是同一根槽(其中一种可能),则即使前序作业有一定延迟,也不会造成翻箱数增加。 针对ACT 的作业特点,说明箱区作业均衡因素与桥吊作业时间的不确定性对配载结果有着潜在的影响。针对箱区作业均衡因素,以最小化装船作业时单位时间不同箱区出箱量的不均衡程度和总装船时间为目标,建立考虑箱区作业均衡因素的ACT 配载混合整数规划模型。针对桥吊作业时间的不确定性,引入“盒式”集合表达不确定因素的取值范围,将确定性配载优化模型转化为考虑桥吊作业时间不确定性的船舶配载鲁棒优化模型,并设计基于编号与排序的禁忌搜索算法对模型进行求解。算例表明,同CPLEX相比,禁忌搜素算法有着很好的求解效率与效果,在不考虑箱区作业均衡因素时(σ2=0)得到的箱区作业不均衡箱量比考虑箱区作业均衡因素时(σ2=2 min)得到的箱区作业不均衡箱量分别高出平均高出17.8%,说明算法可有效降低装船作业的箱区作业量的不均衡程度;而桥吊作业时间的不确定性直接导致“集中配载”的出现,这种“集中配载”能够使配载方案更优。 此外,由于配载的复杂性,进一步细化配载问题的相关约束并提高算法的求解速度是下一步研究的重点,从而帮助这一配载方法更好地应用到码头的实际生产作业中。

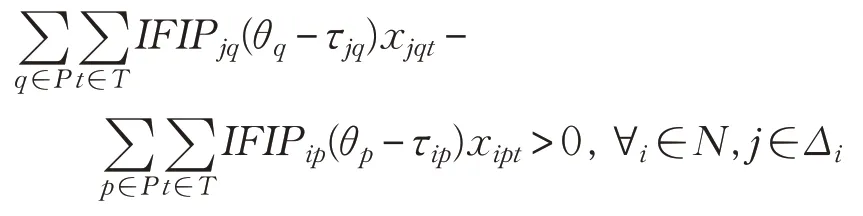




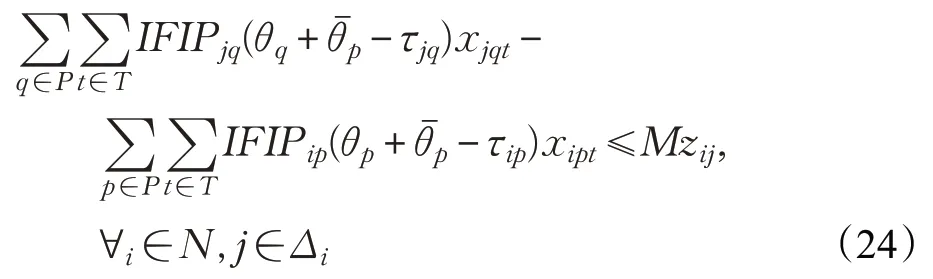
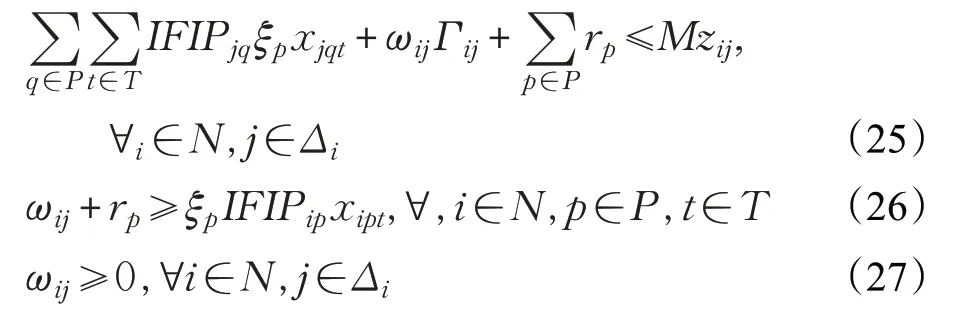



5 基于改进的禁忌搜索算法
5.1 参数设置与初始解


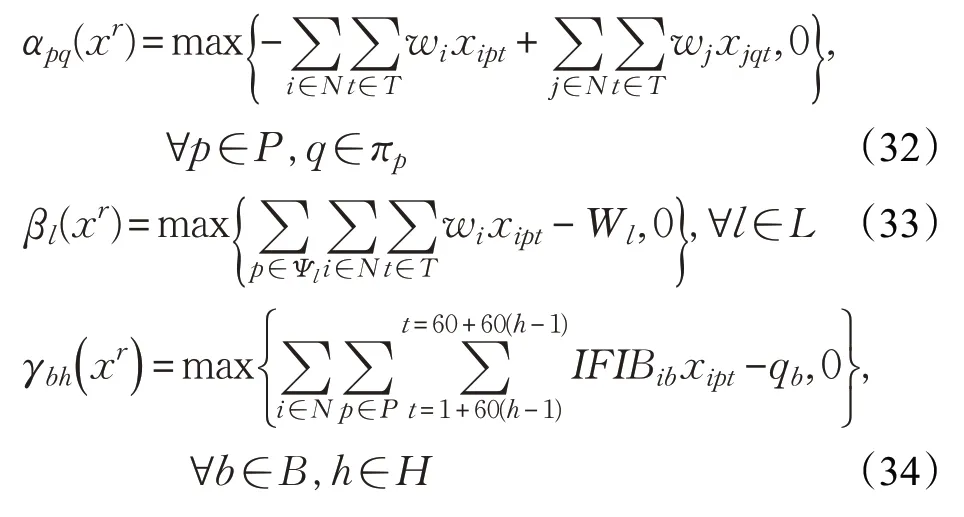



5.2 算法步骤

6 算例分析
6.1 箱区作业均衡因素对配载结果的影响


6.2 桥吊作业时间不确定性对配载结果的影响





7 结论

