考虑性别偏好影响的通勤合乘匹配模型*

何胜学 程 龙 陈经纬 杭佳宇

(上海理工大学管理学院 上海 200093)

0 引 言

车辆合乘一般将现实中司乘匹配时所考虑的时间、起讫点、费用限制等作为约束，以消耗最小出行成本满足最多的出行需求为目标建立模型[1].车辆合乘模型广泛应用于残疾人和老年人的门对门接送[2]或是校车路线规划[3].现在随着“共享”理念推广及移动智能终端的普及，车辆合乘进一步发展为出租车合乘[4]与通勤车辆合乘[5].通过对比合乘和公交的效用差值，毕笑天等[6]对市民出行方式选择进行研究，确定了合乘出行和公交出行的选择依据.在假设司机在新模式下可以以一定代价“购买”其他司机的乘客条件下，Roger等[7]对司乘匹配FCFS(first-come, first-served)模式进行了改进，发现加入乘客交换机制后，整个合乘系统的服务水平得到显著提高.聂昌成等[8]以宁波市为例提出了基于电召平台的出租车合乘模式，并对此合乘模式中的乘客运送以及计费和收益进行了初步分析.

国内外学者对车辆合乘路径规划、费率、车辆调度以及模型算法等领域[9-12]研究较多，较少涉及乘客的合乘偏好等行为决策研究.现实中乘客出于安全等因素的考虑会对合乘者性别进行选择，进而考虑选择是否进行合乘.Yan等[13]在使用时空网络处理出租车的路径规划问题时，将出租车分为普通出租车和只接受女乘客出租车，更加贴近现实中乘客对出租车安全性的需求.程杰等[14]以出租车合乘为背景建立动态车辆合乘模型，并在模型中将出租车和乘客进行了划分，以性别作为车辆和乘客匹配的依据.但上述文献仅考虑固定的乘客组划分，没有考虑现实合乘中存在不同的性别合乘需求以及乘客性别占比变化对合乘匹配效果的影响.针对上述问题，文章对通勤车辆合乘匹配中乘客性别因素的影响进行深入研究.

1 模型说明

1.1 参数说明

z(i,J,(k,g))为司机i与乘客组J可行匹配，通勤乘客上车点和下车点为(k,g)；z0为司机不进行合乘；Z为所有匹配集合.当司机i与乘客组J满足匹配约束时，即z(i,J,(k,g))匹配成功时会产生一组数据(υz,σz)；υz为此次合乘匹配中参与的司机与乘客总人数；σz为合乘给通勤走廊中带来的机动车行驶距离优化值，σz=doidi-(doik+dkg+dgdi)+∑j∈J(dojdj-(dojk+dgdj)).式中：doidi-(dk+dkg+dgdi)为司机i在合乘过程中产生的绕行距离；dojdj-(dojk+dgdj)为乘客j参与合乘后走廊中机动车行驶距离优化值.如果σz>0，则表示进行z(i,J,(k,g))匹配时合乘使得通勤走廊中机动车行驶距离优化值为正，此次合乘是有意义的.

1.2 目标函数

一般可考虑如下通勤合乘匹配的优化目标：①方便通勤者在通勤时段出行，即使得通勤时间段内走廊中最多的司机和乘客(υ值)参与到合乘中来;②最大程度的缓解通勤走廊中交通压力，即使通勤走廊中机动车行驶距离优化值(σ值)最大.

对应上述目标建立的两个目标函数为

(1)

(2)

式中：xiz和xjz为司机与乘客匹配的0-1决策变量.当司机i进行z(i,J,(k,g))匹配时，xiz取1；反之xiz取0.当乘客j∈J进行z(i,J,(k,g))匹配时，xjz取1；反之xjz取0；Jz为z匹配中所有参与乘客的集合；υz为此次z合乘参与的人数，包括司机与所有乘客.

式(1)和(2)分别为模型的目标是通勤合乘参与者数值最大和通勤走廊中机动车行驶距离优化值最大.

1.3 约束条件

模型基本约束为

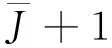
≤Ci

(3)

(4)

toik+τ+tkg+tgdi≤Ti

(5)

(6)

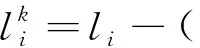
(7)

(8)

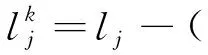
(9)

现实中乘客在与其他合乘者合乘时，会出于自身安全等原因考虑对其他合乘者的性别进行选择.为了全面的描述合乘性别模式，下面针对不同模式下乘客的性别合乘偏好给出相应的模型约束条件.

第一种合乘模式为偏好同性乘客之间进行合乘.假设在这种合乘模式下通勤乘客只偏好和同性的乘客进行合乘.上述偏好同性合乘的模式可表示为

,∀z∈Z,Jz∈zm,

∀z∈Z,Jz∈z

(10)

(11)

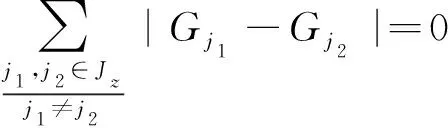
(12)

(13)

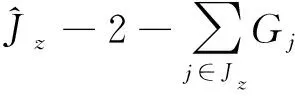
(14)

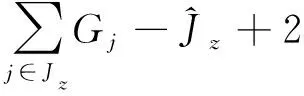
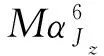
(15)

当乘客组J中仅有一位乘客时，此乘客不受性别合乘模式的约束，此时βJ取值为1，对应约束如下式.

(16)

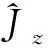
当对乘客组内乘客性别是否满足合乘模式进行判断后，模型需要对满足匹配要求的乘客组和通勤司机进行决策变量赋值.即当乘客组满足性别合乘模式要求或乘客组内容忍系数不小于控制系数时，对应参数xiz和xjz赋值为1；否则赋值为0.约束如下式.

(17)

(18)

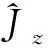
,∀i∈D

(19)

(20)

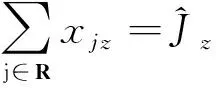
(21)

式(19)为模型中任意司机只能参与到一个合乘匹配中，包括z0.式(20)为模型中任意乘客j只能参与一个匹配中即∑z∈Zxjz=1或不参与匹配即∑z∈Zxjz=0.式(21)为对于∀z∈Z，只有匹配z中所有的乘客参与者都参与到z匹配中时，匹配z才是有效的.其中xiz和xiz分别为0-1决策变量.

2 求解算法

司乘匹配约束中有非线性约束条件，因此所建通勤匹配模型为非线性整数规划模型.以通勤中合乘匹配的具体实现过程为基础，本文设计一种求解上述模型的启发式求解算法.新算法首先确定可行匹配集，然后计算各匹配相关特征量，最后利用分层法确定最佳合乘匹配.新算法不仅可以有效处理模型的非线性约束，而且实现的复杂度较低.

新算法首先将整个路网中所有司机和乘客进行匹配，进行时间、距离和性别约束处理后统计所有可行匹配Z并计算Z中υZ值和σZ值.根据可行匹配z赋值对应控制变量(xjz和xiz)并进行最终模型计算，司机与乘客在无约束下匹配结果见图1.图中有两位司机d1和d2，两位乘客p1和p2.z0为司机没有搭载乘客.两位司机可以选择单独搭载乘客p1，即图中z1和z4的匹配结果；选择单独搭载乘客p2，即图中z2和z5的匹配结果；或是一同搭载乘客p1和p2，即图中z3和z6的匹配结果.

图1 司机乘客匹配结果图

图2为司机乘客匹配结果优化图，由图2可知，有些通勤司机乘客的匹配已经因为不符合约束而不存在，例如司机d2不能一同搭载乘客p1和p2.图中数字为每组通勤司机乘客匹配所产生的两个数据，在模型中用(υz,σz)表示.其中：υz为此次合乘匹配中参与的司机与乘客总人数；σz为此次合乘匹配通勤走廊中产生的行驶距离优化值.当司机d1和d2不参与合乘时就不会产生对应的(υ,σ)，即d1和d2到z0之间数据都为0.

图2 司机乘客匹配结果优化图

针对上文提出的合乘匹配模型，本文设计了三步骤求解算法,如下所示.

步骤2计算可行匹配z对应的(υz,σz).可行匹配z(i,J,(k,g))∈Z中信息包括司机i与乘客组J和合乘的上车点下车点(k,g).由式σz=doidi-(doik+dkg+dgdi)+∑j∈J(dojdj-(dojk+dgdj))计算出对应走廊中机动车行驶距离优化值σ以及匹配人数υ.

步骤3使用分层求解的方法确定最佳合乘匹配.

步骤4考虑到通勤合乘匹配模型首先要方便最多的通勤者出行，以式(1)作为第一目标函数.对于任意匹配z(i,J,(k,g))∈Z，将乘客组J内乘客z(i,J,(k,g))依据合乘模式做匹配.如在同性合乘模式下，依据式(10)～(11)，式(16)～(18)对J内乘客进行if-then约束，判断乘客组J内乘客是否满足同性合乘模式.

当乘客组J满足性别合乘模式时，对乘客j∈J，将乘客j和可行匹配z(i,J,(k,g))对应的控制变量xjz赋值为1，即xjz=1.将司机i和可行匹配对应的控制变量xiz赋值为1，即xiz=1.其他的控制变量赋值为0.将所有控制变量(xjz和xiz)赋值之后，以式(3)～(9)、式(19)～(21)为约束条件，以式(1)为模型的目标函数对合乘匹配模型进行求解.模型求解后会得到模型中最多的通勤合乘参与人数.

步骤5为了使模型在限制最少合乘参与人数条件下实现合乘行驶距离最小化，利用步骤4结果构造如下新约束条件：

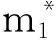
(22)

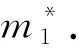
此时求解的模型目标函数为式(2)，约束条件增加式(22).在限制最少合乘参与人数条件下，求解新模型可得到整个通勤走廊中最大的机动车行驶距离优化值.

3 算例分析

算例路网见图3.通勤走廊路网中共有22个节点.其中1～16节点为普通节点，17～22节点为合乘点.实线上数字表示两点间的距离(单位km)，且路网节点之间可以相互直达.设定机动车行驶速度40 km/h，乘客步行速度为5 km/h.司机能接受的最大行程时间T直接设置为司机通勤最晚到达时间与最早出发时间的差值.时间消耗τ值为0.1 h.乘客的容忍系数ϖ由MATLAB软件rand函数随机产生.机动车最大载客量统一设定为4人.

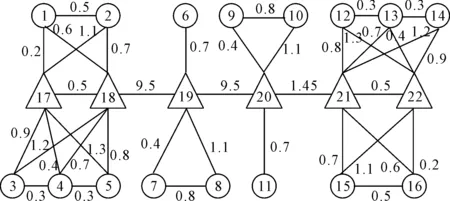
图3 单通道合乘通勤走廊示意图

表1 部分乘客出行信息

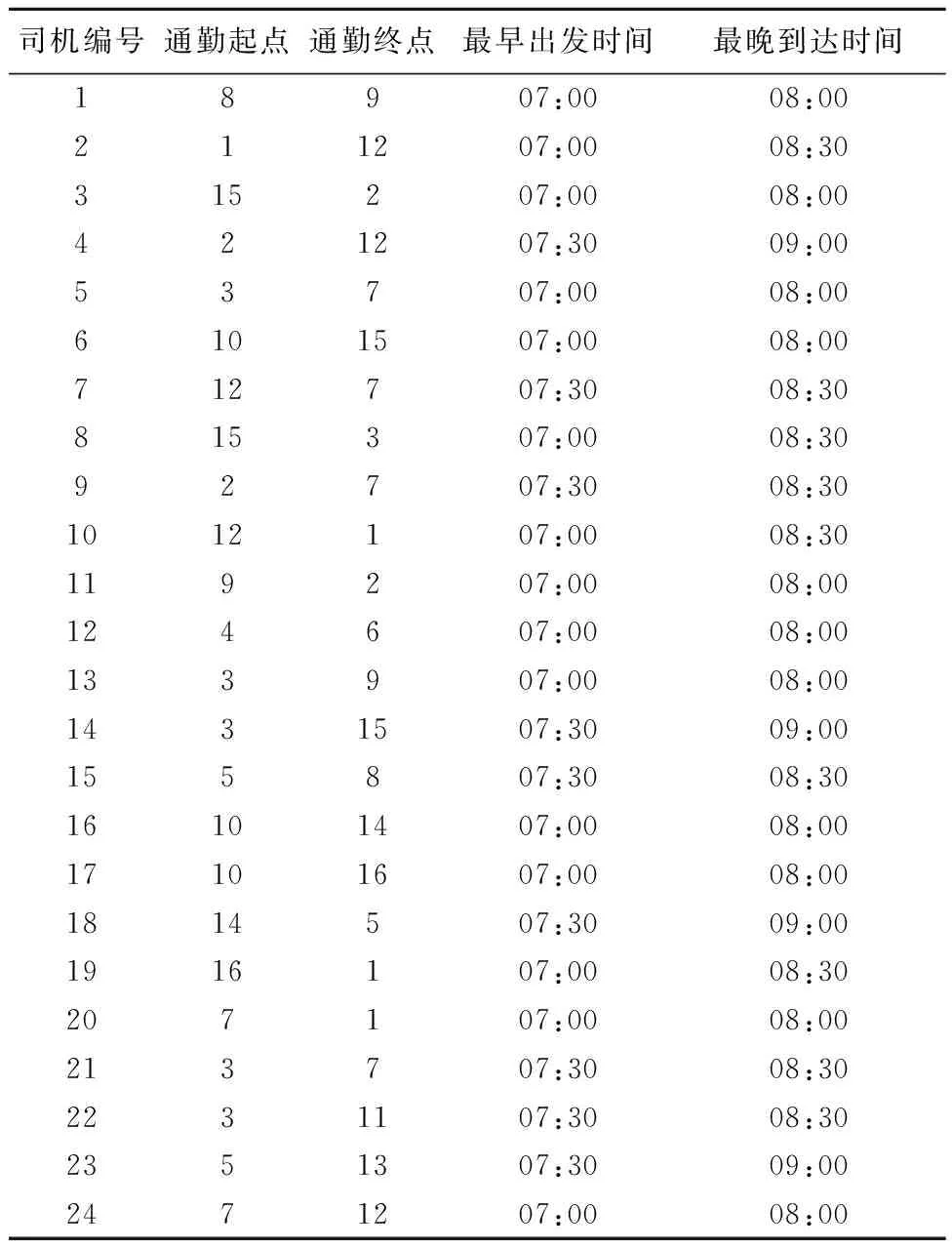
表2 部分司机出行信息

首先考虑第一种合乘模式，即模型约束在性别匹配约束时选择式(10)～(11)加入模型计算.模型的运算部分使用软件MATLAB进行编程运算.模型最终计算结果见图4.

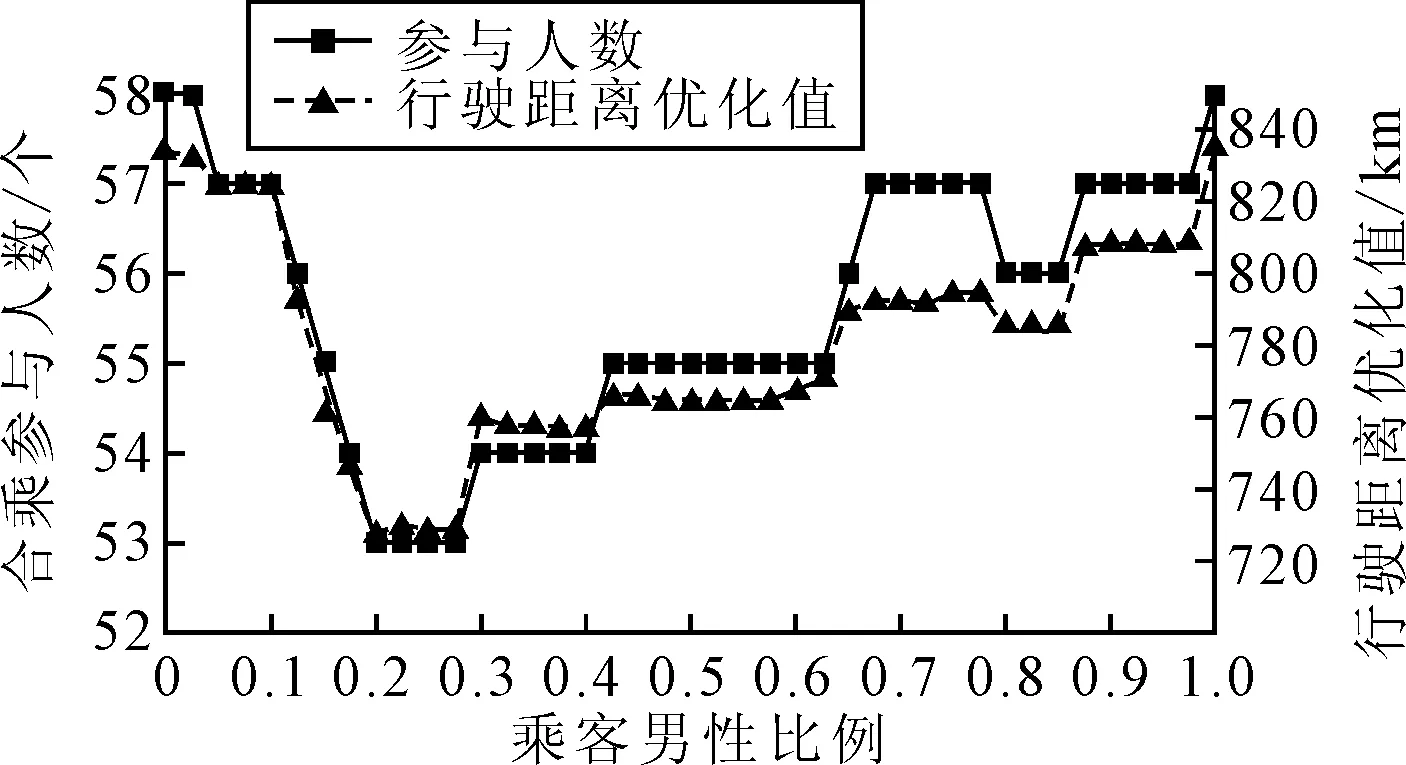
图4 同性合乘模式结果统计图

下面考虑第二种合乘模式，即模型约束在性别匹配约束时选择式(12)～(13)加入模型计算.模型运算结果见图5.

图5 异性合乘模式结果统计图

考虑第三种合乘模式中男性乘客和女性乘客皆偏好和女性乘客进行合乘组成通勤乘客组.即模型约束在性别匹配约束时选择式(14)～(15)加入模型计算.模型运算结果见图6.

图6 特别组合合乘模式结果统计图

从上面对三种性别合乘模式的运算结果可以得出如下结论.

1) 模型输出数据中机动车行驶距离优化值σ与合乘人数υ成正相关.乘客男性比例变化时，图4～6中行驶距离优化值和合乘参与人数的变化趋势相同.因为合乘参与人数变多，说明参与的乘客增多.行驶距离优化值σz=doidi-(doik+dkg+dgdi)+∑j∈J(dojdj-(dojk+dgdj))，其中越多乘客参与通勤合乘，∑j∈J(dojdj-(dojk+dgdj))值会相应增大，σz值也相应增大.因为每位乘客带来的优化值不同，所以行驶距离优化值σ与合乘人数υ呈现正相关趋势，并不是严格正比例关系.

2) 模型输出结果与预期结果相符，印证了包含性别属性匹配模型的有效性.其中在同性合乘模式下，男性乘客或女性乘客占总乘客数比值越高，合乘匹配效果越好；在异性合乘模式下，某一性比乘客数占比越高，越不利于合乘匹配的进行；而在特别组合性别合乘模式下，被偏好性别乘客数越高，匹配效果越好.

图7 控制系数分析统计图

4 结 束 语

针对城市交通中的通勤合乘安全问题，本文提出了一种考虑乘客性别影响的通勤车辆司乘匹配模型.模型中涵盖同性合乘、异性合乘和组合合乘模式，并使用不同约束条件体现性别合乘模式对通勤乘客匹配的影响.算例分析在证实通勤车辆合乘匹配模型有效性的同时，还为现实处理合乘问题中提供以下的指导意见.通勤乘客对合乘同伴性别的偏好会对匹配产生一定影响，为了将负面影响效果降至最小，现实中可以将具有类似合乘偏好的乘客进行分组处理.例如将具有同性合乘偏好的乘客按照性别进行分组，以提高组内乘客某一性别占比；同样对异性合乘偏好乘客进行分组，以均衡组内乘客性别占比，其中男女乘客比值为1∶1时司乘匹配效果为最佳.