结合快速层式DCT和动态LOD的地形压缩绘制技术
杜 德,高保禄,田 力
太原理工大学 软件学院,太原 030024
1 引言
虚拟现实技术具有良好的适应性,在相应的领域中发挥着独特而有效的作用。特别是室外地形场景的绘制中,由于数据规模不断增大,导致需要处理和传输的数据量急剧增加[1-2],虚拟现实技术的普及受到了计算机性能的严重制约。因此,驱使传统的层次细节模型(Levels of Detail,LOD)算法[3]与高性能的压缩算法结合完成地形渲染成为一种主流方向。
针对地形数据的处理方法,主要的研究方法是各种改进四叉树的结构来进行数据处理。罗想[4]提出了一种线性和常规两种四叉树结合的复合四叉树的改进方法,一定程度上减少了无效数据,提高了有效数据的占比,但是只限于较小规模的地形数据,且没有对分辨率进行区分。于卓等人[5]提出了一种将binLBT 压缩解压算法用GPU 进行加速来提高算法效率,但其底层还是基于离散余弦变换(Discrete Cosine Transform,DCT),DCT的块效应和不具备多分辨率的特性使得该算法依然难以满足大规模地形数据的压缩。魏迎梅[6]等人提出了通过小波算法压缩地形数据结合动态LOD[7]完成地形的多分辨率连续绘制,压缩算法与LOD 结合是一个很好地切入点,但小波变换复杂度高,导致绘制过程中帧速率[8]的不稳定性,并且实时性又对处理速度有很高的要求。
基于此,本文深入研究了层式DCT算法[9-10],提出了一种快速层式DCT 嵌入式零树编码算法,并且与动态LOD相结合完成对地形的压缩绘制。先用快速DCT[11-12]代替传统的DCT 对地形数据进行变换,将变换后的系数根据不同频带按原来的空间位置重新组合,对左上角的低频信息执行逆离散余弦变换(Inverse Discrete Cosine Transform,IDCT)作为下层输入,重复上述步骤使其具有多分辨率特性,最后结合基于视点的动态LOD技术完成多分辨率地形的大规模连续绘制。实验结果证明,由于快速DCT 计算简单,变换时间减少,帧速率得到有效提升,同时又能保证稳定的压缩率,极大地减少了对计算机性能的依赖。
2 层式DCT算法
2.1 DCT变换
类似于离散傅里叶变换[13],DCT 是酉变换,并且信号熵和能量在变换前后是守恒的。DCT 的变换核由于是余弦函数,因此时域(或空域)中的n维信号X是可分离的,其正、逆DCT的数学计算公式分别如下:

2.2 层式DCT原理
执行层式DCT 后,整个数据的能量主要集中在左上角的低频部分,是重构整个地形最重要的部分。如图1为三层DCT的分等级带宽示意图。

图1 三层DCT的分等级带宽示意图
首先介绍DCT域抽样和插值的概念:先执行N×NDCT,并提取低频的M×M子块,然后对低频执行M×MIDCT,此为M/NDCT抽样,记为M→N,逆过程称为插值。抽样之后,地形数据分为低通抽样和高通细节。其中“Cosine塔”为低通抽样部分,是重构的主要信息;而“DCT塔”为高通细节部分,只为提高图像清晰度,其量化过程可粗略进行。图2为三层DCT的编解码过程。

图2 三层DCT编解码过程
层式DCT编码的主要步骤:
(1)对第一层原始输入数据执行DCT。
(2)按照原来的空间位置,重组DCT4 个频带子块。如图3所示。

图3 DCT块分割
(3)对低频执行IDCT,作为下层输入,倒L为本层输出数据。
(4)重复步骤(2)、(3),循环执行,满足要求为止。
(5)最后一层直接作为顶层数据。
层式DCT解码的主要步骤:
(1)对顶层数据执行DCT。
(2)下层对上层插值,提高图像分辨率。
(3)完成插值后执行IDCT,作为下层的输入数据。
(4)对输入数据执行DCT,继续插值重复上述步骤,直到得到第一层数据。
(5)最后执行IDCT获得重构地形图像,解码结束。
3 快速层式DCT嵌入式零树编码算法
本文提出的基于快速层式DCT嵌入式零树编码算法是在原来的层式DCT 算法的基础上,将传统的DCT改为无乘法整数DCT 快速算法,先对地形数据进行分层抽样操作,即按步骤分层执行快速DCT 与IDCT,使其具有多分辨率特性,然后再按照零树编码框架进行编码操作[14-15]。解码先按照零树编码框架进行解码操作,对得到的系数按照层式DCT 的解码步骤进行插值,从而得到重构的地形数据。由于现有的层式DCT算法存在大量的DCT计算,所以为了节省时间,满足地形渲染过程中的实时性要求,因此采用DCT 的一种快速实现形式。
3.1 快速DCT算法及流程图
DCT快速算法有众多类型,本文选取对应离散余弦变换类型Ⅱ(DCT-Ⅱ)的一种快速算法。以N=8 为例的快速计算过程如下(流程图如图4所示)。

图4 DCT-Ⅱ快速计算流程图
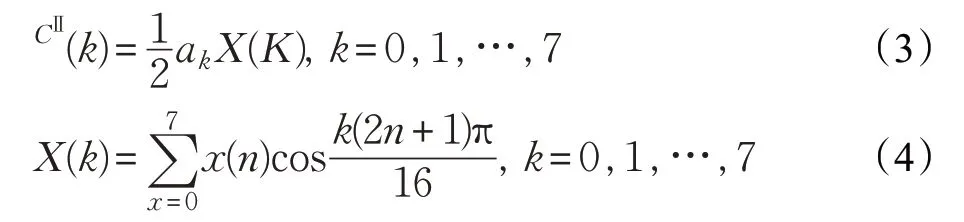
由数学定义可知,余弦函数天然具有对称性,其算法的递推过程可由下式推导而出。
(1)首先计算:

(2)计算四点的值:

(3)最后计算:


上述以N=8 为例的DCT-Ⅱ快速计算过程中需要分别执行12次乘法和29次加法运算。如果对一副8×8个点的图像进行处理时,在编码的过程中需要执行96次浮点数的乘法计算,相对应的在解码时也需要进行96乘法计算,乘法运算消耗系统CPU资源,从而增加变换所消耗的时间,因此需要在此基础上做进一步的改进以提高算法的效率。
3.2 无乘法整数DCT的基本原理及方法
由3.1 节可知,DCT 计算的耗时操作主要在于乘法,因此尽可能减少乘法计算,将会极大地降低DCT的时间复杂度。在此基础上,改用无乘法整数DCT 快速算法[16],通过查表简化蝶形运算将查询结果进行移位累加,并将运算数学公式中的浮点数按一定的倍数放大并取整,最后计算完成后再减小相应倍数。使用快速DCT 算法,一定程度上有效提高了地形数据的压缩效率。
假设离散余弦变换中蝶形运算公式的一般数学形式为T=x1ω1+x2ω2,其中输入数据是x1、x2,常数项是ω1、ω2。为了便于整数形式的DCT 变换,对蝶形运算中的常数项进行放大,将浮点数放大一定倍数并取整,因此,在整个DCT 转换期间,所有操作都将是在整数之间进行,而不是相对复杂的浮点计算,故而可以提升DCT变换的效率。最后,结果减少相同的倍数,并获得DCT后的最终结果。
将数据x1、x2转换为二进制:


其中,ai,bi=0或1,i=0,1,…,n。

如图5 所示,计算aiω1+biω2(i=0,1,…,n),就可以通过位移累加计算T。由于ai、bi取值为0 或1,因此有4种组合0,ω1,ω2,ω1+ω2,又由于ω1和ω2都是常数,可以预先存储在表中,计算aiω1+biω2时根据ai、bi的值就能在预先存储的表中查询,避免了两次乘法和一次加法。aiω1+biω2(i=0,1,…,n)一共有4种情况,已确定的4种不同的结果,如式(17):


图5 查表、位移和累加处理原理
3.3 无乘法整数DCT快速算法流程图
根据3.2 节的基本原理,合并图4 算法流程图中参数的系数,将得到新的形式为T=x1ω1+x2ω2的蝶形运算公式,如图6 所示,其中每个蝶形运算公式中的常数项为:

图6 无乘法整数DCT快速算法流程图

根据上述算法可知,若以N=8 为例进行一维的无乘法整数DCT快速算法,在消除乘法运算之后,只需要进行80次移位运算和95次加法运算。
根据一维DCT的计算方法,在对地形数据进行8×8的二维DCT处理时,首先依据基本原理,将蝶形公式中每个常数项放大1 024 倍后取整。要进行二维DCT,可以先对地形数据做水平方向的一维DCT 运算,然后在对地形数据做垂直方向的二维DCT运算,分别设置L、R标志位,分别表示当前数据左移或者右移的位数,从而得到地形数据经过二维DCT处理后的最终结果集。
3.4 对抽样后的变换数据按照零树框架执行编码操作
如图2 所示,在量化编码阶段,可以使用零树框架编码算法代替原来压缩效率较低的行程编码等方式,提高地形数据的压缩效率。变换后地形数据的系数在给定的尺度等级上与其相同方向的下一等级细尺度上的系数相关联。需要先对系数进行重要程度的判别,筛选出不同阈值平面的重要系数集合之后执行零树编码,其过程如下:
(1)重要系数集合的选择
本文算法的阈值平面选择类似小波变换的零树框架结构,采用2 的正整数幂为基础,有效系数按照阈值平面n的降序从最大阈值平面顺序编码输出,此为有效系数在阈值平面n上的搜索过程。 满足如式(18)为执行快速层式DCT后的有效系数集合Ω。

可以通过函数来确立有效系数的集合,采用下式进行定量计算:

(2)零树预测
地形数据通过快速层式DCT 后,构成了频率依次增高的多分辨率频带系数分解图像。给定阈值T,将系数C(i,j)以及相同方向上较细尺度的系数集合C∏(i,j)(T与C∏(i,j)中每个系数进行比较)与阈值进行比较,判断其重要程度,可将所有系数可分为三类:
零树根 |C(i,j)| 孤立零 |C(i,j)| 正、负有效系数 |C(i,j)|≥T 代表位置信息的有效系数(|C(i,j)|≥T)通过零树结构进行描述之后,信息量大为减少。 (3)用零树框架编码重要图 重要图包括三种要素:(1)零根;(2)孤立零;(3)有效系数。为了简化内嵌编码,将正有效系数和负有效系数与重要图合并编码。采用4种符号:零根、孤立零、正有效系数、负有效系数,使4 种符号与之一一对应。例如: TR(零根)=00,IZ(孤立零)=01 POS(正有效系数)=10,NEG(负有效系数)=11 (4)逐次逼近量化(SAQ) SAQ是内嵌编码的主要实现方法。SAQ是采用一系列可变阈值对其重要性进行判断,T0,T1,…,TN-1,其中Ti=Ti-1/2,初始阈值的取值条件为:|Xj|<2T0,Xj表示所有变换系数。 在编解码过程中将分为主辅两个过程,主过程通过不同的阈值Ti判断是否为有效系数,若是放入辅表,主表记0,不影响下次系数的判断;辅过程由于有效系数在[Ti,2Ti]之间,用“0”、“1”分别表示有效系数在前半区间和后半区间。编码时每次阈值减半,并依次进行主辅过程;解码时辅表选择区间中心值作为重构值,将辅表中的有效系数重新填充到主表中相应位置,重新恢复各重要值的空间位置结构。 快速层式DCT嵌入式零树编码算法流程图,如图7所示。 图7 算法流程图 在使用快速层式DCT嵌入式零树编码对地形数据进行编码之后,本文提出结合动态LOD 技术实现在渲染地形过程中的自适应多分辨率连续绘制。其中,确定有效的可见区域与合理的分辨率等级能够降低地形绘制的复杂度,同时能够确保在地形漫游时提高用户视觉的真实感,也就是说,需要进行视景体裁剪和选择由远及近的分辨率等级提升方法。 在三维空间里,视点除了视景体内的可视区域外,其他区域不可见,因此需要对地形数据进行裁剪。 图8 视景体视域及裁剪 由图8 可知,四边形ABCD 为视景体的可见区域(视域),因此需要计算4个点的坐标值。 计算C、D点的坐标: 已知ED和E的坐标,求得D的坐标: 根据向量CD以及D的坐标,求出C坐标。同理可计算A、B坐标,由此可确定图8中蓝色可视部分的范围。 大规模地形多分辨率连续渲染的关键问题是依据视点的相关位置选择不同的分辨率等级,得以完成层式DCT 的重构过程。重构过程中提高分辨率层级可以通过对每层的系数进行插值即可实现。近视点可以选择高分辨率层级,远视点可以选择低分辨率层级,因此就可以将视域内的地形划分为N个可见范围,选定远视点的最大间隔dmax和近视点的最小间隔dmin,取: 分辨率等级i与视点之间的距离的映射函数为: 根据式(21)可知视域被分割成N个拥有固定分辨率的段,要使视点运动时能够平滑过渡,同时考虑到绘制效率,可继续利用离散化方法将Δd继续细化为n个等级,可以通过阈值筛选方法动态的对距离视点越近的系数进行插值操作,以视距作为度量尺度实现地形的渐进重构。 设视点距离为d,且dmin≤d≤dmax,在第i分辨率等级上,令: 根据式(22)可以选择最大阈值εmax和最小阈值εmin,依据系数分布特点定义筛选阈值的函数: 进行地形层级模型的重构时,考虑到频繁的重构可能会带来系统资源的过度消耗,因此选择一个合适的等级系数n逐步细化 Δd的范围,取 Δd′=Δd/n,当: 取阈值: 进行系数筛选并通过逆变换重构地形。 在视域中以视点位置的变化为基准,在运动过程中选择不同分辨率的层级模型以及同一分辨率下不同精细程度进行绘制重构,因此可以实现地形随视点的自适应连续绘制。 本文实验采用的数据为包含1 025×1 025、4097×4 097 的高程数据和1 024×1 024、4 096×4 096 的纹理数据的The Puget Sound Area 地形数据,该数据由Large Geometric Models Archive at Georgia Tech 网站提供。实验程序是在Windows环境下,使用VS2013和OpenGL完成的。采用的硬件环境为CPUi5-3210M @ 2.50 GHz),显卡(AMD Radeon HD 7500M)。 在保证采样点数目和采样间距相同的情况下,比特率的大小可作为衡量压缩效率的一个因素。传统LOD算法、基于DCT变换的算法、基于小波变换的算法以及快速层式DCT算法的比特率(BPS),如表1所示。 表1 各算法比特率均值 传统LOD算法比特率的值远高于其他3种方法,相同时间间隔内传输的数据量也是最大的;基于DCT 的算法比特率的值相对较低,有一定的压缩率,但其本身所具有的局限性促使其不适合作为大规模地形的连续实时绘制;基于小波变换算法[12]有最好的压缩性能,但小波变换实现困难,导致计算速度较低,从而不能满足实时性的条件;而基于快速层式DCT 算法的压缩性能相对较好,由于采用快速DCT 变换,提高了计算速度,最符合实时性的条件。 各算法的峰值信噪比如图9所示,不管在何种数值的码率之下,基于DCT 算法的峰值信噪比[16]都相对较低,而快速层式DCT 和小波变换算法在相同的码率下具有相似的峰值信噪比值,因此当对地形执行连续实时渲染时,通过使用快速层式DCT 算法也可以获得相对较好的图像质量。 图9 各算法的峰值信噪比 将本文算法的实验数据与传统LOD 算法、基于DCT的算法和基于小波变换的算法进行了比较,如表2所示。 表2 平均帧速比较 在相同的条件下,保持其运动轨迹不变,传统的LOD 算法不需要对地形数据进行额外的压缩解压操作,因此平均帧速率较快,然而随着地形规模和复杂度的不断增加,越来越多的数据会给计算机带来很大的负担,影响计算机的性能,导致帧速率变低以及较大的帧率方差;基于DCT的算法虽然平均帧速较高,但其存在不具有多分辨率特性和块效应的问题,并且压缩比也相对较低;由于计算过程实现复杂,基于小波变换的算法导致计算机的性能偏低,因而帧速率也相对较低。对比之下,快速层式DCT 算法能够找到高压缩性能和高帧速之间的平衡点,使两者都具有较为不错的性能优势。 上述实验结果说明,快速层式DCT 嵌入式零树编码算法在帧速率和压缩性能方面并不是最佳的,但却平衡了两者之间的关系,既可以保证高帧率,又能保持高压缩性能。此外相比于传统DCT 本身存在的缺陷,以及小波变换计算复杂,实现困难等缺点,快速层式DCT算法可以很好地对压缩地形数据,以减少数据传输量并加速地形渲染的渲染速度,同时保证一定的精度,满足人们对实时性的需求。 本文采用快速层式DCT嵌入式零树编码算法结合动态LOD技术完成地形的多分辨率连续绘制。相较于小波变换来说,本文算法由于采用一种快速DCT,计算速率较高,实现较为简单,在保证了较好的压缩性能的基础上,同时也保证了较高的帧速率,减少了在地形渲染过程中数据处理和绘制效率对计算机性能的依赖,本文算法确保了大规模地形实时渲染的及时性和平滑性,使渲染更加连续和平稳。 实验结果进一步表明,本文采用的快速层式DCT嵌入式零树编码算法能够有效提高帧率,同时相比其他算法也具有较高的压缩性能。与现有的结合基于视点的动态LOD 压缩方法相比,快速层式DCT 算法各方面更加均衡。但是,文本算法仍有不足之处,比如数据量过大的话,频繁的正逆DCT 可能会对CPU 造成很大的负荷,从而导致精度缺失问题。因此,下一步将重点放在GPU研究上,以提升算法的效率。
4 基于视点的动态LOD多分辨率地形绘制
4.1 视景体裁剪



4.2 多分辨率等级选择






5 实验结果分析及处理
5.1 压缩性能比较


5.2 帧速率比较

6 结束语

