差分准对立学习多目标蚁狮算法
王亚东,石 全,尤志锋,宋卫星
陆军工程大学 装备指挥与管理系,石家庄 050003
1 引言
在工程领域以及军事领域常遇到多目标优化问题(Multi-objective Optimization Problem,MOP),所求得的最优解集需要满足多个互相冲突的目标。为解决多目标优化问题,很多学者提出了一系列优化方法,从精确算法发展到启发式算法,再发展到元启发式算法,近些年又提出了超启发式算法。由此可见多目标优化问题一直是研究的热点和难点问题。
智能优化算法作为元启发式算法,对解决多目标问题具有很强的鲁棒性和适用性。常见的智能优化算法有PSO[1]、蚁群算法[2]、狼群算法[3]等仿生群体智能算法,以及NSGA[4]、差分进化[5]、基于分解的进化算法[6]等多目标进化算法。其中,Mirjalili 提出的蚁狮算法(ALO)是一种群体智能优化算法,它通过模拟蚁狮捕食蚂蚁的过程以获取问题的最优解[7]。为利用蚁狮算法求解多目标问题,Mirjalili 又提出了多目标蚁狮算法。算法利用不同个体的Pareto支配关系寻求最优解,该算法相对于MOPSO 和NSGA-II 等经典算法的优越性已得到了验证[8]。由于蚁狮算法的优越性,该算法很快得到了应用和推广。赵世杰等人对蚁狮算法进行了改进,用于优化SVM 的参数[9];Yao 等人利用蚁狮算法解决路径规划问题[10];Zawbaa 等人将蚁狮算法用于特征选择[11]。
但是,在原始的蚁狮算法中蚂蚁个体的位置更新过分依赖精英蚁狮的信息。导致算法在求解多目标问题时容易过早收敛,不利于寻求全局最优解。而差分进化算法拥有较为成熟的进化策略,为提升算法性能目前已经出现了大量改进的变异、交叉以及选择算子[12]。因此本文利用差分进化的思想,提出一种能够同时充分利用当前种群和精英个体信息的变异策略。同时,还提出准对立学习策略以改善种群的特性,提高个体在整个解空间内的探索能力(exploration)和局部开发能力(exploitation)。
2 相关研究
2.1 蚁狮算法
蚁狮算法是模拟自然界中蚁狮建造陷阱捕食蚂蚁的过程来寻求最优解集,因此在蚁狮算法中有两个种群,即蚁狮和蚂蚁。蚁狮捕食过程主要由五个基本步骤组成:蚂蚁的随机游走、蚂蚁落入陷阱、蚂蚁滑向蚁狮、蚁狮捕获蚂蚁以及蚁狮重构陷阱。蚁狮算法的基本步骤正是模拟以上过程,其数学描述和模型如下所示。
(1)随机游走机制,公式如下:
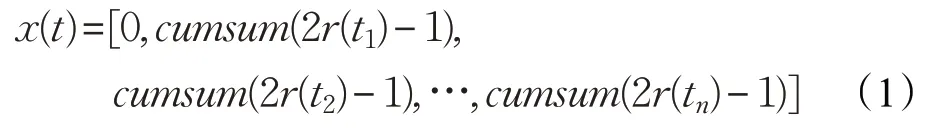
其中,cumsum为累积和,t是迭代次数,n是最大迭代次数。是与t相关的随机函数,rand满足[0,1]均匀分布。
为了保证个体在搜索空间内随机移动,防止其超出边界,需要对个体的位置进行规范化处理:

(2)通过改变蚁狮周围的随机游动来模拟蚂蚁掉入陷阱的过程,公式如下:

其中,ct和dt分别是第t次迭代时所有变量的最小值和最大值;是第j个蚁狮在第t次迭代时的位置。
(3)通过适应性地缩小蚂蚁随机游走的范围模拟蚂蚁向蚁狮滑落的过程,其公式如下:

其中,系数I满足,随着迭代次数的增加而逐渐增大。t是迭代次数,T是最大迭代次数,ω是随迭代次数而动态调整的参数。
(4)模拟蚁狮捕获蚂蚁的过程如下:

选择并储存适应度值最优的蚁狮作为精英个体,精英是唯一影响蚂蚁位置蚁狮。即蚂蚁向着随机选择的蚁狮以及精英蚁狮进行随机移动,其移动公式如下:

(5)重构陷阱。采用一个外部存档(Archive),来存储Pareto 支配解集。采用小生境技术衡量存档中解的分布,每个解的邻域均为给定的半径。用每个解邻域内的其他解的个数衡量该解的分布性,邻域内解越多则表示越密集,解越少则越稀疏。
2.2 差分进化策略
差分进化算法(Differential Evolution,DE)是在遗传算法等基础上提出的,通过模拟基因遗传学中的变异、交叉和选择来不断更新个体,逐步找到最优的个体种群。与遗传算法不同的是,差分进化算法的变异个体是由父代差分个体生成,并与其他父代个体交叉生成新个体,直接与其父代个体进行选择。目前常用的差分进化变异策略如下[13]所示。
(1)DE/rand/1策略:

(2)DE/rand/2策略:

(3)DE/best/1策略:

(4)DE/best/2策略:

(5)DE/current-to-best/1策略:

(6)DE/current-to-rand/1策略:

其中,Fi是控制参数为定值;xri为种群中随机选取的个体,xi为发生变异的个体,xbest为适应度最优的个体,且满足xi≠xbest≠xri。
以上变异策略能够利用父代种群的信息产生新的个体,其中策略(3)、(4)、(5)还利用了种群中最优个体的信息优化个体的变异方向。但是,通过实验发现(见本文实验部分),单纯将这些变异策略引入蚁狮算法并没有很好的改善蚁狮算法的性能。因此需要借用差分进化思想,提出与蚁狮算法相适应的变异策略。
2.3 准对立学习策略
传统元启发式算法通常对一组随机的初始解进行寻优,而随机产生的初始解可能距离最优解很远,因此算法需要很长时间去向最优解收敛。反向学习策略是机器学习中的一种优化策略,它要求在每次优化时同时对当前解和其对应的对立解进行检验并择优作为新的解。在黑盒优化中,反向学习策略得到的很好的应用,其优化结果通常更加接近优化问题的最优解。
对于一个可行域为[a,b]的实数x,定义其对立数ox如下:

但是,反向学习仅考虑某个解的对立数,而为了增加种群的多样性,保证全局寻优能力,本文采用(Quasi-Opposition Based Learning,QOBL)策略对初始种群进行优化[14]。定义x的准对立数qox如下:

则对于D维蚂蚁个体,其准对立个体中第i维变量的值为。
在得到准对立种群后,将其与原种群个体混合,并择优作为新的种群。
3 改进多目标蚁狮算法
要想将传统差分进化思想应用到多目标蚁狮优化算法中,需要克服两方面的问题。首先,传统差分进化的变异策略都是针对单目标优化问题,因此要解决由单目标向多目标的转化。在单目标优化问题中,通过单纯比较适应度函数值即可对个体的优劣进行排序。而多目标优化中需要同时考虑个体的多个目标,因此不能通过比较适应度值大小确定最优个体xbest。本文引入非支配排序思想,首先根据蚂蚁个体的Pareto支配关系找出非支配解,将非支配个体放入外部存档中作为蚁狮种群。其次利用小生境技术(Niche)对存档中的蚁狮种群进行排序,选出精英蚁狮个体。则精英蚁狮的优于其他蚁狮个体,所有的蚁狮个体优于蚂蚁个体。
其次,原蚁狮算法中蚂蚁位置更新公式仅使用了外部存档中蚁狮的信息,抛弃了蚂蚁种群的信息。这可能导致算法过早收敛,不利于全局探索。而传统差分进化的变异策略则强调了蚂蚁种群的信息,没有充分发挥蚁狮信息的作用,不利于算法的收敛。因此要考虑如何全面利用种群和蚁狮的位置信息。因此,本文提出了一种新的蚂蚁位置更新公式:
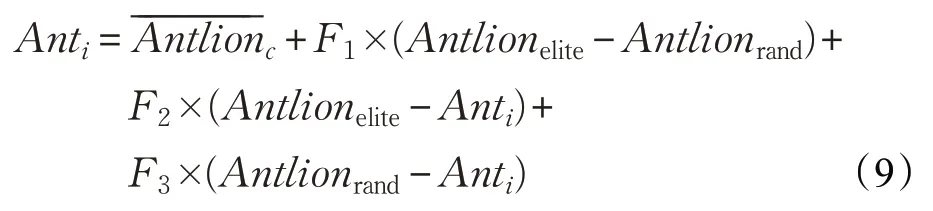
公式(9)可以充分利用当前种群的信息,以及蚁狮的位置信息,保证种群向精英蚁狮移动。针对求目标函数最小值的多目标优化问题,图1 给出了其几何解释。图中的红点分别表示蚂蚁个体以及从外部存档中选出的精英蚁狮和随机蚁狮,蓝点表示的位置。由精英蚁狮和随机蚁狮构成的边为(Antlionelite-Antlionrand)、(Antlionelite-Anti)和 (Antlionrand-Anti)三个向量。按照的三个向量方向(图中蓝线)运动至新的位置即更新后的蚂蚁个体(图中黑点)。从图中可以看出通过式(9)的矢量变换,原蚂蚁个体Anti将有效地向真实Pareto前沿面移动,算法的收敛性得到了提升。

图1 位置更新公式的几何解释
在每次迭代结束产生新的蚂蚁种群后,求其准对立个体,并将两个种群混合后根据支配关系择优作为新的种群进入下次迭代。伪代码如下:
算法准对立差分多目标蚁狮算法
2. 设置种群规模,外部存档规模,产生初始种群
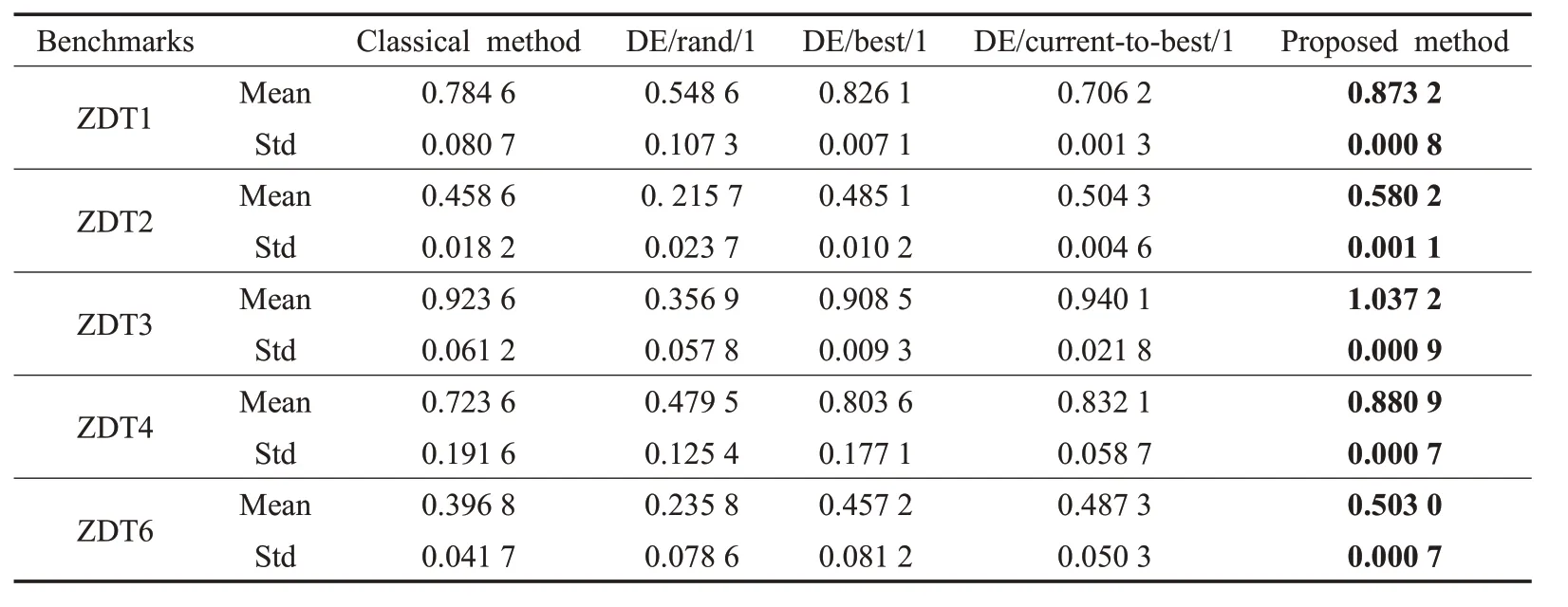
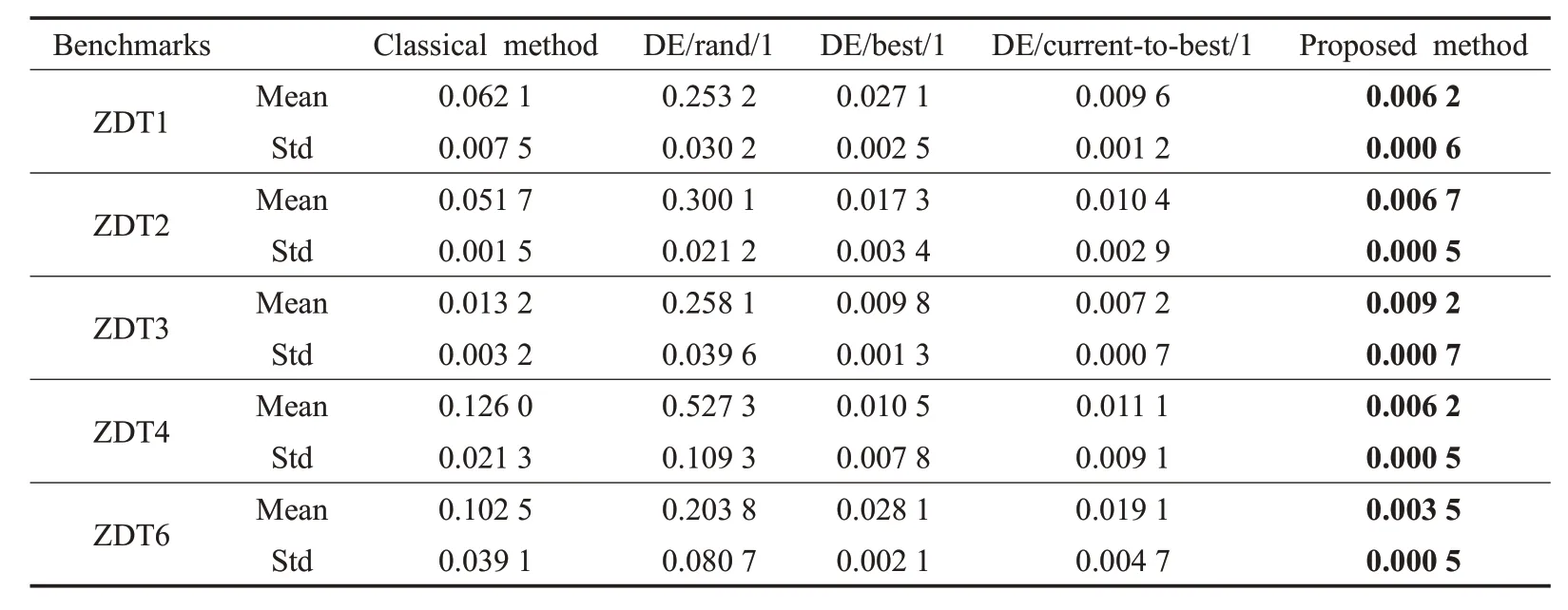
3. While (t 4. fori=1∶n 5. 计算蚂蚁种群个体适应度函数 6. 根据个体支配关系,更新外部存档(蚁狮种群) 7. 计算存档中蚁狮个体的拥挤度,选出精英蚁狮和随机蚁狮 8. 根据公式(9),更新蚂蚁的位置 9. end for 10. fori=1∶n 11. forj=1∶d 12. 根据公式(7)和(8)计算个体向量的准对立向量 13.Mi,j=(aj+bj)/2 14. If (Anti,j 15. 16. else 17. 18. end if else 19. end for 20. end for 21. 将准对立种群与原种群混合,根据支配关系和拥挤度择优产生新的种群 22. end while 对于多目标优化算法,其算法的性能主要体现在收敛性(conversation)以及分布性(distribution)上[15]。收敛性描述了算法求得的结果向真实帕累托前沿面(Pareto Front,PF)的逼近程度。算法的收敛性越强,表示其求得的解集越接近真实最优解,结果也越精确。分布性描述了算法求得的结果在目标空间上的分布特性,一方面应当尽可能分布在整个PF 上,另一方面应当尽量均匀的分布。算法的分布性越强,表示算法的全局探索能力越强。 为衡量算法的以上两个性质,在诸多评判指标中,由于IGD(Inverted Generation Distance)和HV(Hyper Volume)指标因其可以同时反映算法的收敛性和分布性而应用最为广泛[16]。因此,本文也采用IGD 和HV 作为算法性能的评判指标。 IGD描述了算法结果到参考点的平均距离,其值越小,表明所求得的解集越逼近真实PF,并且具有较好的分布性。计算公式如下: 其中,P∗为参考点,即真实PF 上的点的集合。P为算法求得的解的PF。d(z,P)是P到P∗上的点z的最小欧式距离。为P∗的规模。 HV描述了算法求得的点和参考点在目标空间构成的超体积。其值越大表明了算法的收敛性和分布性越好,计算公式如下: 其中,Λ 表示勒贝格测度,P为算法求得的解,xref为参考点。 为了研究该改进算法的性质,本文选取ZDT 系列测试函数对算法进行验证[17]。实验参数设置、策略的表达式以及F取值[18]见表1。 为检验本文提出的差分进化策略对算法的优化效果,将其与经典蚁狮算法以及传统的差分进化策略优化的算法进行对比。在未采用准对立策略的基础上分别采用不同的变异策略对原始多目标蚁狮算法进行优化。算法分别在各标准测试函数上进行测试,实验结果如图2所示。 图2 从左至右分别为原始MALO 算法、DE/rand/1策略改进算法、DE/best/1 策略改进算法、DE/current-tobest/1 策略改进算法以及本文提出的DEQOMALO 算法。从上至下分别为五个测试函数。从图中可以直观观察算法在各测试函数上结果的分布情况。从图中第一列中可以看出,MALO 算法在求解ZDT 测试函数时最优解集基本落均在真实PF 上,但是在求解ZDT1 和ZDT2时并为均匀地分布在整个PF上,即分布性表现较差;从图中第二列中可以看出,采用DE/rand/1 策略时,算法求得的最优解基本上全未能落在PF 上,表明此时算法的收敛性和分布性均很差,主要是因为该策略采用完全随机的变异策略,未能使种群向精英蚁狮的位置移动。从图中第三列和第四列可以看出,DE/best/1策略以及DE/current-to-best/1 策略下算法求得最优解均落在PF上,但是同样未能分布在整个PF上,其求解所有ZDT测试函数时分布性均较差。而图中最后一列为本文提出的改进策略,可以看出算法的最优解在所有测试函数的目标空间内都能够均匀广泛的分布在真实PF 上,算法的收敛性和分布性均为最优。 表1 实验变异策略与参数设置 图2 不带准对立学习策略的最优解分布 为了进一步定量分析算法的性能,将几种算法在各测试函数上分别运行30 次,记录每个算法对应每个测试函数的HV和IGD指标的均值和标准差,其结果见表2和表3。表中的最优值用加粗数字表示,对于HV指标其值越大为最优,对于IGD 指标其值越小为最优,对于标准差其值越小表明算法越稳定。观察指标的均值,可以看出本文提出的算法得到的HV 指标均取得了最大值,IGD 指标均取得最小值,表示DEQOMALO 的收敛性和分布性较其他算法均为最优。观察指标的标准差,可以看出本文提出的DEQOMALO 算法的稳定均优于其他算法。 表2 HV指标的均值和标准差 表3 IGD指标的均值和标准差 图3 带准对立学习策略的最优解分布 为进一步分析准对立学习策略对算法的影响,将准对立策略引入各算法,再次对ZDT 系列测试函数进行实验。实验结果如图3所示。 可以发现,加入准对立学习策略后,DE/best/1策略、DE/current-to-best/1策略以及本文提出的策略下的改进算法的最优解均能够落在真实PF 上,而且均广泛而均匀地分布在PF 上,表明准对立学习策略能够大大改进算法的性能。从图中前两列可以看出,原始蚁狮算法和DE/rand/1策略算法效果虽然仍然较差,但是相对于图2中未引入准对立策略的算法有较大的提升。尤其是DE/rand/1 策略下算法的最优解收敛性改善明显,其最优解均落在了PF 上。因此,加入准对立学习策略在一定程度上提升了算法的性能。 表4 HV指标的均值和标准差 表5 IGD指标的均值和标准差 表4和表5记录了各算法在各测试函数上分别运行30 次后的HV 指标和IGD 指标的均值和标准差。从表中可以看出,一方面,本文提出的算法优于经典蚁狮算法以及传统差分进化策略改进的算法;另一方面,通过和表2、表3结果的比较,在引入准对立学习策略后的算法要优于不带准对立策略的算法,在DE/rand/1、DE/best/1 和DE/current-to-best/1 策略下改进算法上体现尤为明显。 为了提高蚁狮算法在解决多目标问题时的精度和全局搜索能力,提出改进的多目标蚁狮算法。在研究多目标蚁狮算法的基础上进行了以下改进:首先,引入差分进化的思想,提出了一种既可以充分利用种群信息又可以利用精英蚁狮信息的查分进化策略,代替原算法的个体更新机制。其次,采用准对立学习策略对种群进行优化,一方面可以增加种群的多样性,另一方面有利于提高算法的收敛速度。为了验证本文提出的算法的性能,选取了经典标准测试函数,并以原始多目标蚁狮算法和传统进化策略优化的算法为参照进行了数值仿真。仿真实验结果表明该改进算法在求解各测试函数时,较其他算法均取得了良好的收敛性和分布性,并且改进的多目标蚁狮算法具有更高的稳定性。因此,本文提出的基于差分进化的准对立学习多目标蚁狮算法在求解多目标优化问题时具有良好的适应性和鲁棒性。4 仿真实验及结果分析
4.1 实验设置

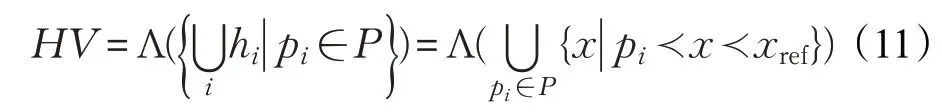
4.2 进化策略对算法的影响




4.3 准对立学习策略对算法的影响

5 结论

