数学建模竞赛培训和数学建模课程设计探讨

摘   要：随着计算机技术的迅速发展，数学的应用不仅在工程技术、自然科学等领域发挥着越来越重要的作用，而且在经济、管理、金融、生物、医学、环境、地质、人口、交通等新领域都有广泛的应用。数学要应用于工程领域就离不开数学建模。数学建模作为一门理论联系实际的课程，已经普遍在全国高等学校中开设。重点对数学建模竞赛培训和课程教学实践过程进行总结和探讨，涵盖课程目标、课程设计、教学方式等。

关键词：数学建模;课程设计;教学方式

随着计算机技术的迅速发展，数学的应用不仅在工程技术、自然科学等领域发挥着越来越重要的作用，而且在经济、管理、金融、生物、医学、环境、地质、人口、交通等新领域都有广泛的应用。

在解决实际问题方面，数学建模就是关键一环。数学建模根据实际问题来建立数学模型，对数学模型进行求解，然后根据结果去解决实际问题。当需要从定量的角度分析和研究一个实际问题时，人们就要在深入调查研究、了解对象信息、作出简化假设、分析内在规律等工作的基础上，用数学的符号和语言作表述来建立数学模型。

数学建模作为一门理论联系实际的课程，已经普遍在全国高等学校中开设。目前，福建江夏学院结合数学建模竞赛培训，将数学建模作为一门公共选修课，开展课程教学。本课题重点对数学建模竞赛培训和课程教学实践过程进行总结和探讨，涵盖课程目标、课程设计、教学方式。

1    数学建模实例分析—以2019高教社杯全国大学生数学建模竞赛A题为例

1.1  问题分析

A题是根据柴油机工作过程设计给出的，完整题目详见全国大学生数学建模竞赛（CUMCM）网站上“高压油管的压力控制”[1]。在工作过程中，為了保持压力和喷油量的稳定，必须建立数学模型和设计算法来确定从高压油泵进入高压油管和从高压油管喷出的燃油量，从而确定单向阀的开启时长、凸轮的转速、减压阀的控制策略，并通过高压油管内压力随时间的变化来展示所得结果的合理性。

1.2  模型建立和求解

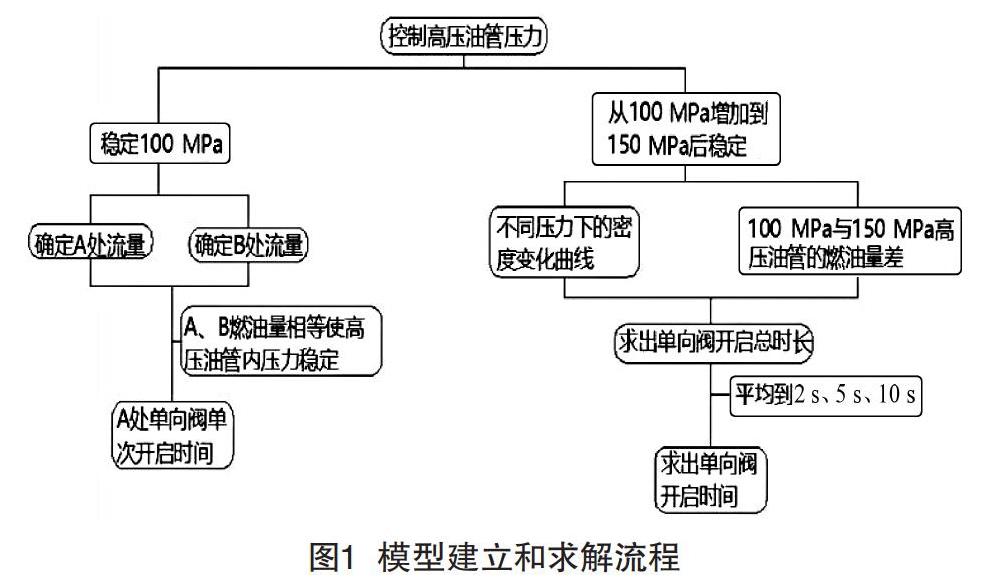
对于A题中的第一个问题，根据题目所提供的数据给出燃油密度随压力变化的函数关系式。在固定单向阀开启时长的情况下，给出高压油管内压力和密度随时间变化的模型或算法。给出压力稳定在100 MPa和压力从100 MPa增加到150 MPa时以及压力稳定在150 MPa时的模型或算法、单向阀开启时长和3种时间里的调整优化策略。求解流程如图1所示。

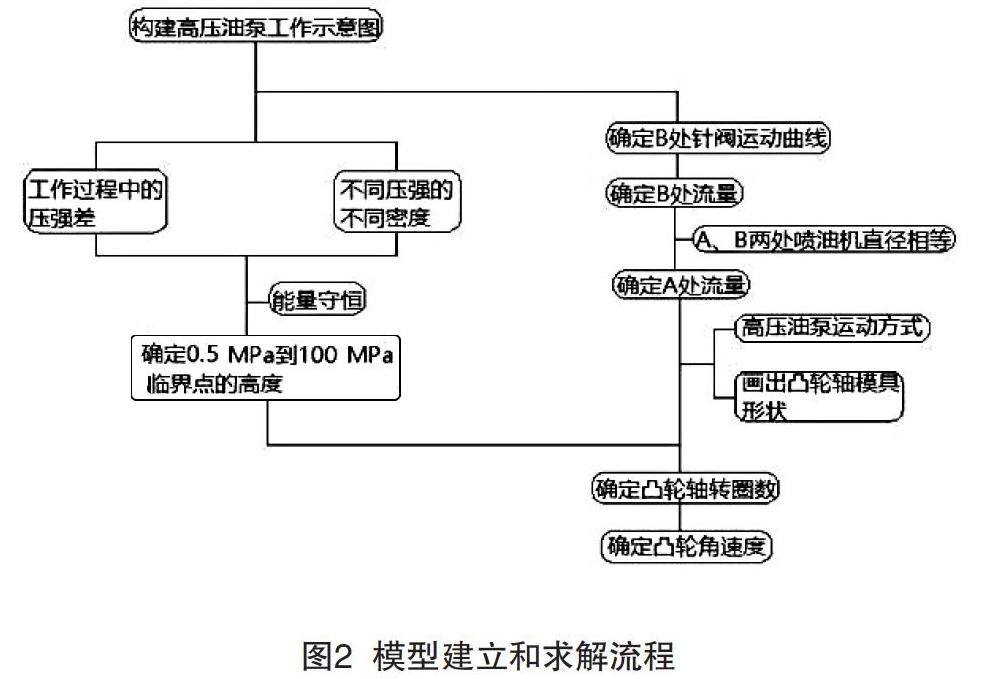
对于A题中的第2个问题，进入高压油管的燃油量由凸轮柱塞腔和高压油管的压力差决定，从喷油嘴喷出的燃油量由高压油管内的压力决定，高压油管内的压力由进入和喷出的燃油量决定。在固定凸轮转速的情况下，给出凸轮柱塞腔内和高压油管内压力和密度随时间变化的模型和算法。最后，给出保持稳定压力和优化凸轮转速的模型和结果。求解流程如图2所示。

对于A题中的第3个问题，当有两个喷油嘴时，在模型和算法中明确指出每个喷油嘴开始喷油的时间，给出凸轮转速的最优模型和计算结果。当考虑减压阀时，给出减压阀开启时间和凸轮转速的优化策略。

从建模实例来看，数学建模需要具备问题分析的能力、快速学习的能力[2]，需要一定的数学基础，需要逻辑论证的能力，如何通过合理的课程内容设计和课程教学设计来培养学生的这些能力，是数学建模课程设计需要重点考虑的问题。

2    课程目标

2.1  培养学生对问题抽象、简化和提出问题、建立模型的能力

数学建模是将实际问题中的因素进行简化、抽象变成数学中的参数和变量，运用数学理论进行求解和验证，并确定最终是否能够用于解决问题的多次循环。因此，数学建模课程，需要培养学生对问题的抽象、简化和提出问题，并建立数学模型的能力。数学建模能力包括转化能力、数学知识应用能力、创造力和沟通与合作能力。数学建模主要表现为：发现和提出问题，建立和求解模型，检验和完善模型，分析和解决问题。

2.2  提升数学论文写作能力

论文，是探讨问题、描述研究成果的一种手段。无论是理论研究还是技术研究，成果要进行展示，基本都要写成论文或研究报告，数学建模也一样。最后，学生要通过一篇逻辑清晰、结构合理、论述完整的论文，展示数学建模成果，展示解决实际问题的结果。因此，论文的写作能力是一项重要基础能力。在数据建模课程中，要对学生论文写作进行训练，提升学生的论文写作能力。

数学论文，注重定义、定理的推导和证明。数学论文的写作过程，要体现严密的逻辑，语言要简洁，符号定义要有广泛的普适性。因此，课程需要对数学论文的写作规范、论文的格式、论文的组织进行基础的培训和训练。

3    教学设计

3.1  数学基础训练

数学建模没有统一的方法和模式，但存在一些基本方法，教学中要对学生进行基础的训练，让学生掌握这些基本的建模方式，将有效提升其建模能力。在教学过程中，要把握好难度，采取渐进式教学，在初期，主要让学生掌握数学建模的基本步骤和方法，学会对具体问题进行分析、抽象，对数据进行采集、分析，判断数据间的关联关系，形成初步建立、应用数学模型的意识。基础的建模方法，如关系分析法、数据分析法、图标分析法、类比法等均为基础的方法。另外，还要关注一些依托数学基础理论的建模方法，例如微分建模方法、积分建模方法、统计建模方法、线性规划建模方法等。要让学生建立起对数学建模的基本认知，对常见的数学模型有所了解，并学会运用基础的建模方法。

3.2  案例教学

为提升学生的实战能力，福建江夏学院每年会组织数学基础较好的学生进行数学建模集训，一般在暑假进行。学生通过学校的数学建模选修课，对数学建模的理论、基础方法、常见数学模型有一定的认知后，在数学建模集训阶段，建议以范例教学为主，使用以往全国大学生数学建模竞赛真题来进行训练，主要训练学生使用数学软件能力和写作能力。以获奖优秀论文为范例，进行解析教学，对论文进行剖析和点评，提高学生的写作能力。

3.3  翻转课堂

学生完成基础理论的学习并接受一定的建模训练后，可在培训的最后阶段采用翻转课堂的教学形式，活跃课堂气氛，提高学生的学习兴趣，并在学生自主讲解案例的过程中，强化对基础建模方法的认知，提高基础建模方法的应用能力[3]。

翻转课堂改变了传统的机械式、安排式、灌输式教学模式，把课堂的主动权交给学生，使学生的学习积极性得到了充分的发挥。学生在课前根据自己的动态需求来安排学习，课后老师精准辅导，有针对性地在课堂答疑解惑，整个教学过程兼顾不同需求层次学生的学情。

3.4  “互联网+”

“互联网+”主要指借助慕课等网络资源，在有限的课堂时间里，无限拓展课堂容量，包括师生互动与教学评价。在教学设计中，可以将该课程所需的理论知识和背景资料，以慕课或微课的形式提供给学生，使书面知识立体生动起来[4]。在学生学习过程中，个人兴趣可能有不同导向，反映在课堂上就是学生能够提出带有个性特征的问题。

4    问题探讨

4.1  课程学习和竞赛培训的关系

选修课程的学生，更多是对数学建模竞赛感兴趣的学生，课程更应该注重于基础能力的培养，同时，通过举办数学建模竞赛集训的方式，来提升学生的竞赛技能。竞赛集训需要更多关注数学建模软件的应用、论文的写作技能等。通过此类课程的衔接，把数学建模思想、数学建模理论、数学建模竞赛培训和参加数学建模竞赛联动起来，形成了一个相互促进、相互补益的有机体[5]。

4.2  问题分析的过程和结果的关系

进入21世纪以来，创新意识已深入人心，培养创新思维也是举办全国大学生数学建模竞赛的初衷。创新能力因人而异，但数学能力却是衡量一个人的数理逻辑水平的最好表述，不是一朝一夕能够养成的，需要在长期的锻炼中慢慢积累、沉淀和升华[6]。只有在分析问题的过程中百般求索，在得出結果时精益求精，数学能力才能得到精炼，才能迸射出创新的火花。

[参考文献]

[1]中国工业与应用数学学会.全国大学生数学建模竞赛[EB/OL].（2019-09-12）[2020-06-10].http：//www.mcm.edu.cn/html_cn/node/b0ae8510b9ec0cc0deb2266d2de19ecb.html.

[2]张深林.浅谈数学建模中快速学习能力的应用[J].科教文汇，2019（10）：64.

[3]张深林.“翻转课堂”在“管理运筹学”课程中的应用与实践[J].科教文汇，2016（4）：81-83.

[4]武帮杰，杜 轩，李浩平，等.基于翻转课堂理念的“互联网+”实验教学模式改革探究[J].科教文汇，2019（10）：73.

[5]杨真真，李 雷，赵洪牛，等.基于数学建模竞赛的“六位一体”创新人才培养模式实践研究[J].实验室研究与探索，2018（9）：172.

[6]刘法贵，岳红伟.关于数学建模教育与数学建模竞赛的思考[J].华北水利水电大学学报：社会科学版，2019（3）：34-38.