层次分析法在初中阶段学业水平评估中的应用

杨辉

【摘要】评价初中生学业水平，传统方式是依据期中、期末成绩。本文利用层次分析法，将平时成绩考虑其中，重新赋予期中成绩、期末成绩权重，得到一种新的学业水平评价方案：5.7%作业+1.3%课堂表现+1.6%+29.7%期中成绩+61.7%期末成绩。

【关键词】学业水平  平时成绩  层次分析法

【中图分类号】G63  【文献标识码】A 【文章编号】2095-3089（2020）13-0243-01

1.背景

现阶段，“分数至上”是评价初中生学业水平的主要方式。两场考试（期中、期末）成为了衡量学生学习好坏的“金标准”。湖北荆州成丰学校曾将期中考场布置在小树林里，并宣成桌子间距大，可以防止抄袭[1]。以此，“分数至上”论被推上风口浪尖。为了打破唯分数论对初中生学业评价的固化模式，综合素质评价将结果性评价与过程性评价融合，以期客观、全面地评价其学业水平[2]。但是，未建立完整的指标整合体系、评价标准不明确、评价技术支撑不到位等问题使得综合素质评价后继乏力[3]。

在美国的中学生评价体系中，更注重学生的发展，不做横向比较。学生的整体综合性是主要考核标准，如学科成绩、社会实践、推荐信、爱好特长等[4]。英国的评价体系，则更多地偏向过程性，将初始成绩作为起点，特定年份或者课程阶段为终点，以此来评价学生的学业水平[5]。

如何取长补短，做到中西方学业评估的融合，对倡导素质教育的今天，迫在眉睫。大学的课程考核中，包括了平时成绩、期中成绩、期末成绩。期中，平时成绩的占比有效地提高了课堂教学。平时成绩的考核注重考查学生的综合素质和能力，同时提高学生的课堂主动参与性[6]。将平时成绩考核“下沉”到初中，作为考核初中生的学业水平的一部分，在现阶段的学校中使用不多。但是，如何设置平时成绩、期中成绩、期末成绩的权重分配则变得至关重要。

2.层次分析法在初中阶段学业水平评估中的应用

20世纪70年代，美国运筹学家Saaty首次提出了层次分析法[7]（Analytic Hierarchy Process，简称AHP），它将与结果有关的元素拆分成目标、准则、方案等层次，在此基础上，进行定性、定理分析。

2.1学业水平评价体系建立

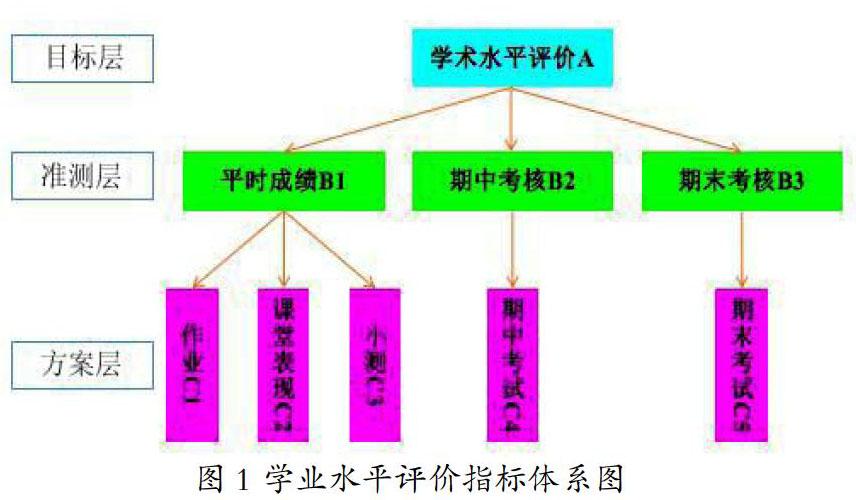
初中阶段学业水平评估的目的是为了客观衡量学生的综合水平，同时让学生明白学习的过程是非常重要的一个环节。这里，我们选取平时成绩、期中成绩期末成绩3个一级评价指标，5个二级指标，构造了如图1所示的指标体系。

2.2确定指标权重&一致性检验

根据AHP法，建立了指标体系之后，两两比较同一层次指标因素的影响程度，采用1-9标度法，如表1所示，进而确定出判断矩阵A、B1。

经计算，各指标权重分别为：WA=（0.086，0.297，0.617）T，WB1=（0.659，0.156，0.185）T。

最大特征值：

根據表2，一致性指标显示，得到CA=？姿A-n/（n-1）Rn=（3.14-3）/（3-1）×0.52=0.0364，CB1=？姿B1-n/（n-1）Rn=（3.03-3）/（3-1）×0.52=0.0078。因为CA、CB1<0.1， A、B1具有满意一致性，则以上计算的权重值是可以接受的。因此，学业水平评价方案为：5.7%作业+1.3%课堂表现+1.6%+29.7%期中成绩+61.7%期末成绩。

2.3 案例研究

选取A、B两位同学的平时、期中、期末成绩，在此学术评价标准下，来评价其学业水平。如表3所示。

从表3中可以发现，根据原标准的评判标准，忽略掉平时成绩产生的影响，期中和期末各站50%的权重，则A、B两位同学最后的表现一样，无法做出区分。而如果根据新标准，重新赋值期中、期末的权重占比，同时考虑平时成绩带来的影响，从而可以发现，A同学的整体表现要优于B同学。

结论

在评价初中生，学业水平的过程中，根据层次分析法，将平时成绩考虑其中，对平时、期中、期末成绩重新赋予权重，得到一种新的学业水平评价方案。这种方案，可以更加科学的衡量学生的整体表现。同时，让学生们明白平时表现的重要性，更加积极地参与课堂。但是，也需要看到层次分析法在比较指标之间重要性的主观性带来影响，这会极大地影响各项的权重占比，从而对学术评价体系产生影响。

参考文献：

[1]半山.“树林考试”是分数至上论的极端表现[J].甘肃教育， 2014（12）：14-15.

[2]许丹丹.综合素质评价背景下的初中生学业水平评价研究[D]. 2016.

[3]马跃.中小学综合素质评价的现状、问题与对策[J]. 教育测量与评价：理论版， 2015（6）：18-23.

[4]刘军.管窥美国中学生的评价方式[J]. 出国与就业（就业版）， 2010（2）：78-79.

[5]陈剑光，牛月蕾，徐丹.英国中小学教育增值评价改革及启示——基于兰开夏郡学校效能增值评价的实验研究[J]. 教育研究与实验， 2013（3）：22-26.

[6]李国强， 许钒. 大学课程成绩评定体系中平时成绩评定权重浅析[J]. 吉林教育， 2016（13）.

[7]邓雪，李家铭，曾浩健，等. 层次分析法权重计算方法分析及其应用研究[J]. 数学的实践与认识， 2012（7）：93-100.