课堂中渗透数学思想方法四策略

胡珊珊

[摘 要]数学教学中，教师适时渗透数学思想方法，有助于学生理解和掌握所学的数学知识。因此，教师在教学中可通过尝试分类、体会抽象、引导推理、建立模型等策略渗透数学思想方法，提升学生的数学核心素养。

[关键词]小学数学;数学思想方法;渗透;策略

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2020）15-0024-02

数学思想方法是数学的灵魂，是学习数学的通法。那么，数学课堂中，教师如何对学生进行数学思想方法的渗透呢？下面，笔者根据自己多年的教学经验，谈谈课堂中渗透数学思想方法的策略。

一、尝试分类，渗透数学思想方法

分类可以帮助人们更好地了解事物之间的相同点与异同点，进一步获得对事物的本质认识。因此，数学课堂中，教师应根据具体的教学内容，引导学生运用分类思想来解决相关问题，促进学生对所学知识的深入思考与理解，为学生知识体系的建构奠定基础。

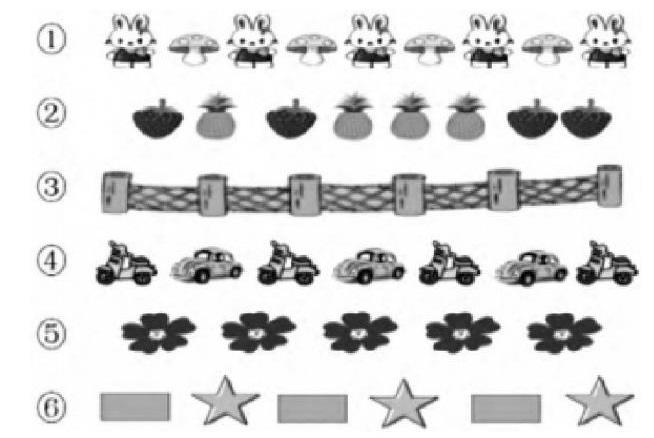
例如，教学《间隔排列》这一内容时，为了促进学生对间隔排列的认识，教师出示下图让学生仔细观察，要求学生从中找出与图案①相似的图案。观察比较后，学生发现图案③④⑥和图案①相似，因为这几组图案不仅包含了两种不同的物体，而且这两种物体是一个间隔着一个排列的。教师顺势告诉学生：“像这样一个接着一个物体排列的，这种规律就叫作间隔排列。”然后教师让学生数一数图案中每种物体的数量，并填写在相应的表格里，这样旨在使学生能根据物体数量的特点推导出其中的排列规律。接着，教师继续提问：“在什么情况下，图案中两种物体的数量正好相差1？”这样教学，不仅使学生对间隔排列的规律有进一步的理解与认识，而且能培养学生留心观察周围事物的良好习惯，促使学生主动去探究更多的数学规律。

这里，教师组织了两次分类活动，不仅有助于学生由浅入深地理解与把握间隔排列的规律，明晰间隔、排列、一一对应之间的内在联系，而且有利于学生在探究过程中提出有价值的问题，初步感知其中的数学思想方法。

二、体会抽象，渗透数学思想方法

抽象是人们对客观事物本质属性与规律的分析、概括，是数学学习中最常用的一种思维方法。數学教学中，教师引导学生在经历数学知识产生、形成和发展的过程中进行抽象，可以培养学生的抽象思维，提升学生解决问题的能力。

例如，教学《角的初步认识》这一内容时，教师让学生先观察教具——三角板，然后问学生：“你们知道这个三角板的角指的是什么吗？谁来指一指？”学生根据自己已有的知识经验来指角，无一例外，学生指的角都是三角形的顶点部分。教师继续提问：“这个三角板只有一个角吗？你能在黑板上对着三角板，把它的角画出来吗？”与教师的预设一样，学生画的角只是一个点。针对这一情况，教师追问：“其他同学呢？你们的想法和这位同学一样吗？”这时教师把三角板移开，让学生观察对比点与角的区别。在教师的启发引导下，学生明白点不是角，要想确定一个图形是不是角，不仅要看它的顶点，还要看它的两条边。在此基础上，教师让学生运用学过的有关角的知识来判断哪些图形是角，哪些图形不是角，深化学生对角的理解。最后，教师让学生总结概括出角的概念，即角有一个顶点、两条边。这样从直观到抽象地进行教学，使数学思想方法在学生心中生根发芽，促进学生数学学习能力的提升。

这里，教师从实物上的直观角展开教学，引导学生真正经历找角、画角、议角的全过程，既深化了学生对角的理解，又渗透了数学思想方法，促进学生对角的概念的建构。

三、引导推理，渗透数学思想方法

所谓推理，指从一个或者几个已知判断出发，按照事物之间的逻辑关系得出一个新的判断的过程。数学教学中，教师引导学生运用推理分析与解决问题，不仅有助于学生把握数学知识的本质，而且能深化学生对所学知识的理解，有效培养学生分析问题和解决问题的能力。

例如，教学《轴对称图形的认识》这一内容时，教师借助多媒体向学生展示一张蝴蝶的图片、一张北京天坛公园的图片、一张飞机模型的图片，让学生仔细观察并说说这些图片的特点。仔细观察后，学生得出结论：这些图形两边的大小和图案完全一样。顺着学生的思维，教师说道：“我们把这样的图形叫作轴对称图形。”然后教师出示图形（如下）并提问：“这些图形的形状和大小一样吗？它们是轴对称图形吗？”在问题的引领下，学生通过比较、讨论、操作、验证得出以下结论：第一个图形，梯形平移后两边可以完全重合且大小相等;第二个图形，梯形旋转后两边可以完全重合且大小相等;第三个图形，梯形对折后两边可以完全重合。但是，第一个图形和第二个图形不能称之为轴对称图形，只有第三个图形才能称为轴对称图形，因为第一个图形和第二个图形并不具备第三个图形对称的特点。这样教学，使学生深刻地理解了轴对称图形的特征。

这里，教师列举具体的图形，引导学生通过观察、操作来验证图形是不是轴对称图形，自然而然地对学生进行了数学思想方法的渗透，使学生经历了从具体到抽象、从特殊到一般的归纳推理过程，促进了学生数学学习能力的提升。

四、建立模型，渗透数学思想方法

在数学教学中，建立数学模型，运用模型思想解决数学问题，可以让学生经历由实际问题抽象出数学模型的过程，使学生真正获取知识，发现知识之间的内在联系，实现知识体系的建构。

例如，教学《除法的初步认识》这一内容时，为了使学生更好地了解“按给出的份数进行平均分”“按给出的每份数进行平均分”这两种情况，理解和掌握除法的法则与意义，教师组织学生进行实践活动。通过实践活动，学生明白：把8个桃子平均分给2个小朋友，其实就是看8里面有几个2;同样，有8个桃子，每个小朋友分得2个桃子，也是看8里面有几个2，就可以分给几个小朋友。这两种除法计算在本质上是一样的，所以教师要重点引导学生说出“一共有多少个，每几个为一份，可以分成几份”或“一共有多少个，平均分成几份，每份有几个”。这样教学有助于学生建立数学模型，提升数学教学质量。

这里，教师引导学生建立数学模型，不仅能促进学生对除法的理解与掌握，而且于无形中对学生进行模型思想的渗透，获得了好的教学效果。

综上所述，数学课堂中，教师要善于根据具体的教学内容和学生的认知规律，有意识地对学生进行数学思想方法的渗透，彰显数学思想方法的价值，让数学教学更有效、更有魅力。

（责编 杜 华）