基于问题引领的数学教学浅析

钟宏伟

[摘 要]问题引领的数学教学，可以促进学生对数学知识的主动建构，提升学生的数学学习能力。数学课堂中，教师可通过提出问题给予学生引领与点拨，使学生真正经历数学化的学习过程，从而完善自身的认知结构，实现深度学习。

[关键词]问题引领;数学教学;认知;思维

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2020）15-0022-02

建构主义认为，学生的学习应该是在已有知识经验基础上进行的一种主动建构活动，而不是被动地接受教师给予的知识和经验。可在平时的教学中，教师虽然提出了许多问题，但是由于设计或组织不当，问题过于分散、琐碎，导致学生大多都是在教师的推动下被动地去发现问题、探究问题与解决问题。

所谓问题引领，指能够把有层次、结构化、可扩展、能持续的核心问题贯穿于整个课堂教学的一种方法。它可以使学生的思维真正由表层走向深入，最大限度地激发学生的探究兴趣，帮助学生更好地理解所学知识。那么，教师怎样才能通过问题引领，帮助学生完成数学知识的主动建构呢？数学课堂中，教师应为学生营造生动活泼、自由轻松的学习氛围，使学生在问题引领下能够展开积极的思考与探究，提升数学学习品质。

一、由点及面，完善认知

现行的数学教材，有些知识以“碎片化”的形式存在，教师只有及时地引导学生梳理所学知识，学生才能把学过的知识连点成线、连线成网。这样学生的数学学习才会经历由知识结构向认知结构发展的过程，提升学生的数学学习质量。

例如，教学《多边形面积的整理与复习》时，教师的常规做法是先引领学生对本章节内容进行回顾：“这一单元，我们总共学习了哪些图形面积的计算公式？想一想，它们各自是怎样推导出来的？”在学生回答后，教师继续提问：“推导多边形的面积计算公式，什么图形起到的作用最大？这个图形与其他图形之间有着怎样的关系？”然后教师引领学生对学过的图形面积知识进行回顾与总结，帮助学生完善多边形面积计算之间的结构关系。从整个教学过程来看，教师提出的问题虽然能够帮助学生回顾已学过的图形面积计算公式，有助于学生数学知识网络的建构，但是在这个知识建构的过程中，由于教师“牵”的过多，“放”的不够，反而不利于学生主动认知的发展。因此，教师在教学中可从知识整体联系的角度出发，提出核心问题“知道我们为什么要先学习长方形的面积计算吗”供学生思考，帮助学生串联起多边形面积计算的相关知识。在问题的引领下，长方形与平行四边形、平行四边形与多边形之间的关系被学生主动梳理和建构，促进了学生自主学习能力的提升。

由此可见，数学教学中，教师应根据具体教学内容的特点进行由点及面式的提问，帮助学生把所学知识串联、建构起来，使学生对所学知识的记忆更深刻，获得显著的教学效果。

二、由疑及证，解惑释疑

古人云“学起于思，思源于疑”“学贵知疑，小疑则小进，大疑则大进”。因此，教师可充分利用学生数学学习中的困难点、疑惑点、矛盾点设计问题，激发学生主动观察、分析探究的欲望，使学生对问题的思考更全面、更清晰、更透彻、更合理，进而发现数学知识之间的内在联系，提升数学学习能力。

例如，教学《2、5的倍数的特征》时，教师让学生先在百数表中把2、5的倍数圈出来，再总结出2、5的倍数的特征。探究学习后，有学生提出质疑：“判断一个数能不能被2与5整除，为什么只看个位上的数？”面对学生的质疑，教师问道：“如果十位上的数是1，这个1表示多少？如果用小棒（1捆）来表示的话，要看它是不是2的倍数，就得2根2根小棒地分，大家想一想，这捆小棒能被分完吗？如果十位上是其他的数呢？如果是百位、千位、万位上的数呢……”这样教学，以问题引领，解惑释疑，促进了学生学习能力的提升。

由此可见，数学教学中，教师可从学生的质疑入手提问，使学生在思考分析、动手操作中对所学的数学知识有更深刻的了解和认识，提高学生的学习效率。

三、由浅入深，逐步提升

数学课堂中，教师由浅入深地提出问题，有利于学生对问题的探究和学习新知。因此，教师教学时应从学生的认知水平出发，找准学生新知的生长点，帮助学生沟通新知与已知之间的联系，使学生对所学知识记忆深刻。

例如，教学《3的倍数的特征》时，教师从学生已有的知识经验出发提问：“2的倍数有什么特征？5的倍数有什么特征？3的倍数的特征能否用2与5的倍数的特征来解释说明呢？”在学生说出自己的看法后，教师追问：“你想用什么办法来研究3的倍数的特征呢？”然后教师让学生在百数表中把3的所有倍数圈出来，并提问：“想一想，3的倍数可能会有怎样的特征？你能用小棒等学具，探究出3的倍数的特征吗？”最后，教师让学生总结出3的倍数的特征。上述教学，教师提出的问题看似简单，实则每个问题的目标指向都非常明确，从回顾复习2与5的倍数的特征，到学生自主猜想3的倍数的特征，再到自主研究、总结交流，使学生由浅入深地理解新知，收到了显著的教学效果。

这里，教师从学生已有的知识经验出发，先提出浅层次的问题，再逐步深入，引导学生经历归纳推理到演绎推理的全过程，使学生直观地感受到数学知识之间的内在联系，真正理解了所学知识。

四、由表及里，发展思维

学生提出的问题大多从直觉经验产生，因此在数学教学中，教师可基于学生的直觉经验，引领学生分析与解决问题，帮助学生对所学知识进行理性的概括，使学生从关注知识转向关注知识背后的数学思想方法，提升学生的数学核心素养。

例如，教学《对称、平移和旋转》这一内容时，练习中有以下一题。

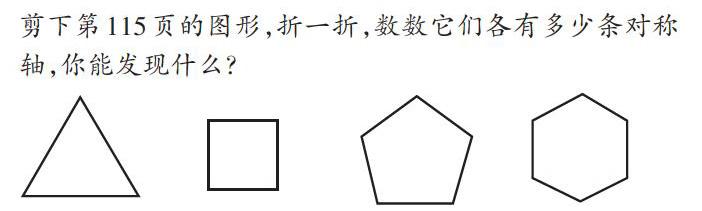
[剪下第115页的图形，折一折，数数它们各有多少条对称轴，你能发现什么？]

对于这样的习题，教师通常的做法是让学生先画出每个图形的对称轴，然后交流自己的发现。这样教学直奔目的，不利于学生思维的发展。要想提升学生的操作能力与思维能力，教师在学生画对称轴之前不妨先提出问题，让学生思考后再操作：“（1）这是一些特殊的图形，先观察一下，你能说出它们的名字吗？你能发现它们特殊在什么地方吗？（2）你能把正三角形和正方形所有的对称轴都画出来吗？（3）你能用画正三角形与正方形对称轴的方法，把正五边形与正六边形的对称轴也画出来吗？”在学生回答问题后，教师再提出问题：“数一数各图形的对称轴，说说自己的发现。”“你知道边数越多的图形有什么特点吗？”“圆有多少条对称轴，你知道吗？你是怎么发现的……”这样的问题由于指向不同，促使学生在探究问题的过程中不断深入思考，从而促进了学生思维的发展。

这里，教师从对称轴的画法及图形本身的特点提问，使学生对对称轴的认识从感性层面上升到理性层面，培养了学生的思维能力。

综上所述，问题是数学的心脏，基于问题引领的数学教学，不仅能有效激活学生的思维，提升学生解决问题的能力，而且可以培养学生的问题意识，为学生的全面发展奠定基础。

（責编 杜 华）