夯实学科基础 突出能力考查 打造高素质教师队伍——中小学教师资格考试数学学科知识与教学能力“学科知识”模块考情分析与测评

罗成禹

夯实学科基础 突出能力考查 打造高素质教师队伍——中小学教师资格考试数学学科知识与教学能力“学科知识”模块考情分析与测评

罗成禹

（教育部考试中心，北京 100084）

加强教师资格考试的实证研究，对提升试题质量，促进高素质数学教师队伍发展具有重要意义．分析2012年下半年至2019年上半年共14次笔试“数学学科知识”模块试题及实测数据，从考查内容、试卷结构、考情分析3方面加以阐释．从试卷质量上看，“数学学科知识”模块试题结构合理，难度适中，具有较高的信度和效度，为国家选拔学科水平合格的数学新教师奠定坚实基础．从考生在数学学科知识的考情上看，报考高中教师的考生在各维度上的表现全面优于报考初中教师的考生；师范生同样在各个方面优于非师范生．学科知识是教师专业发展的基础，考生在数学学科知识的掌握和应用上还需进一步提高，“学科知识”模块也将进一步在夯实学科基础，突出能力考查上下功夫．

数学学科知识；考查内容；知识分项；能力侧面；试卷结构；考情分析

中共中央国务院《关于全面深化新时代教师队伍建设改革意见》（中发〔2018〕4号）（以下称《意见》）强调：“为深入贯彻落实党的十九大精神，造就党和人民满意的高素质专业化创新型教师队伍，需大力振兴教师教育，不断提升教师专业化素质能力．”《意见》还指出：“严格教师准入、提高入职标准，重视思想政治素质和业务能力……逐步将初中教师学历提升至本科，有条件的地方将普通高中教师学历提升至研究生．”[1]高素质专业化创新型是新时代教师队伍的新要求，高标准严要求重德才是新时代教师准入的新趋势．

2011年，教育部启动实施中小学教师资格考试项目改革，增设了科目三《学科知识与教学能力》，结束了师范生毕业即可拿证的“特权”时代，激发了学生学习的主观能动性，推动了师范院校培养模式改革的步伐，为全面提升中小学及幼儿园教师质量奠定了坚实的基础．数学，是从义务教育到高中阶段贯穿始终的必修主科，对人的能力培养与发展是全面而深远的．数学教师的学科知识研究不仅是教师专业发展的重要组成部分，也是教育改革发展研究的重要组成部分[2]．同时，作为科目三报考人数最多的科目之一，对《数学学科知识与教学能力》的试题研究与考情分析对于提升数学教师培养质量有着积极的影响．分析了2012年下半年至2019年上半年近7年共14次笔试试卷及测评结果，以“学科知识”为切入点，分别从考查内容、结构特点、考情分析3方面加以阐述，以期为中学数学教师专业成长起到积极的导向作用，并促进试题质量不断提升．

1 中学数学教师资格考试“学科知识”考查内容

1.1 学科知识的分项分类

《数学学科知识与教学能力》考试大纲（“学科知识”模块部分）[3]，详见表1．

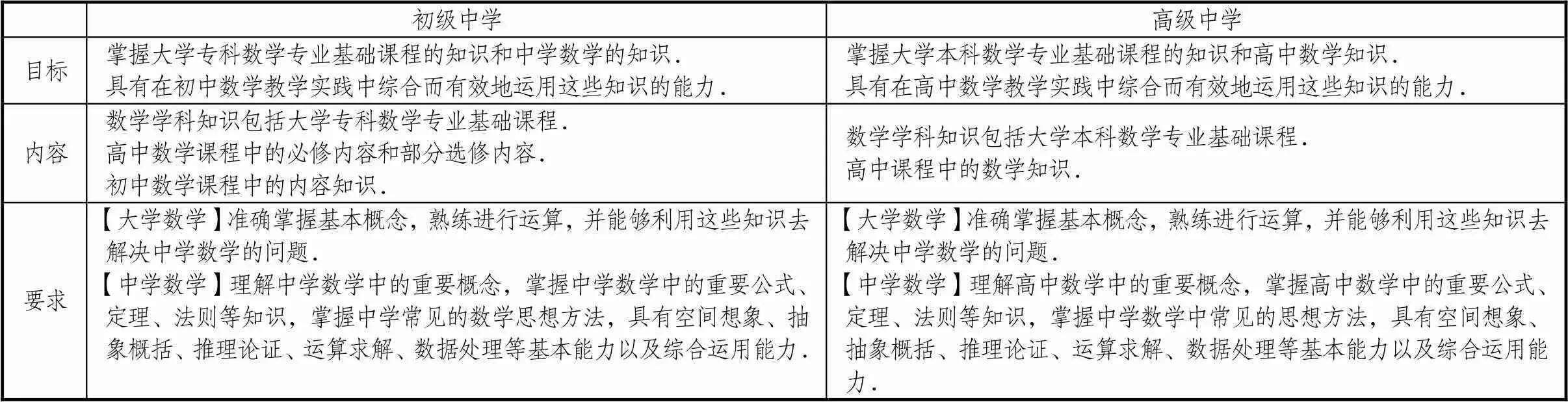
表1 《数学学科知识与教学能力》考试大纲（“学科知识”模块部分）

在学科知识方面，大学数学专业基础课程部分着重考查基本、常用知识点的概念、性质、相关定理及其应用．中学数学部分则多与课程知识、教学理论、教学实践相结合，强调对于相关知识的深入理解与应用，重点考查核心基础内容，具有较强的应用性，与高等数学具有紧密联系或者对于引导学生进一步深入学习理解数学公式、定理、思想具有重要作用的内容[4]．为方便后文进一步分析研究，根据《数学学科知识与教学能力》考试大纲（以下称《考纲》）要求，按照学科内容分类，将“学科知识”部分又进一步细分成“分析”“代数”“几何”“概率统计”4个分项（图1），这既涵盖了《考纲》要求的大学数学专业基础课程与中学数学课程知识，又展现了大学高等数学与中学初等数学辩证统一的关系．中学与大学的数学学科知识不是割裂的，中学数学为大学数学的学习奠定了基础，大学数学为中学数学的理解深化了内涵．

图1 《数学学科知识与教学能力》“学科知识”模块分类

在学科能力方面，《考纲》中明确提出“空间想象”“抽象概括”“推理论证”“运算求解”“数据处理”“综合运用”共6大能力．同时，注意到作为大纲命制依据的《中小学和幼儿园教师资格考试标准（试行）》（以下称《标准》）中关于“分析”一词，总共出现了29次，可见《标准》对于新任教师具备分析能力的看重，因为分析是抓住事物本质进而解决问题的起始步骤，更贯穿在教学的各个环节中．虽然《标准》中的“分析”并不特指对数学问题的分析，但数学为人们提供特有的、具有典范意义的思维方式，这种思维方式对于从事各种职业的公民在岗位上获得成功与发展都是重要的智力保障[5]．一方面从政策导向上，强调分析能力，突出数学学科知识中能力的考查；另一方面，从后文分析试题数据可操作性上考虑，在6大能力的基础上，再细分出“分析判断”能力．在试题分类上，题干中带有“正确”“成立”等字眼的试题，在学科能力考查上都划归为这一类，主要集中在客观题中．而主观题往往综合性强，难度大导致得分低，这更是淡化了试题所考查出的考生分析能力，对于简答题、解答题，根据阅卷评分参考中解题步骤所赋分值及各项能力考查侧重程度的不同，从部分试题侧重考查的“推理论证”“综合应用”等能力侧面中剥离出分析判断的能力，突出分析能力，给与权重量化分析．从而将从“空间想象”“抽象概括”“推理论证”“运算求解”“数据处理”“综合运用”“分析判断”共7大能力侧面进行分析．

在认知维度方面，本着“高素质，专业化”高标准严要求的原则，《大纲》开篇明义第一句话在考试目标中就强调“学科知识的掌握和运用”，毕竟给学生一碗水，老师要有一桶水，甚至要终生学习能活水涌流．所以对于新任老师，数学学科知识的认知维度标准不仅仅停留在“了解”“理解”层面，更需要“掌握”并“应用”．虽然要求高，但从考情分析的角度维度有些单一，并且缺乏量化的依据，所以暂不对认知维度进行分析讨论．

1.2 学科知识的考查要求

按照《考纲》对于数学“学科知识”的考查要求可分为以下3个层面．

（1）理论层面要求：掌握基本概念、公式、定理、法则、数学思想方法．突出基础，强调掌握，培养新教师严谨认真，吃苦耐劳的品质，体现育人导向和专业化导向．

（2）应用层面要求：利用大学数学知识解决中学数学的问题．突出联系，强调应用，培养新教师勤学思辨，学以致用的品质，体现育人导向和实践导向．

（3）能力层面要求：具有空间想象、抽象概括、推理论证、运算求解、数据处理等基本能力以及综合运用能力．突出能力，强调全面，培养新教师坚持不懈，善思明辨的品质，体现育人导向和能力导向．

师者传道，一名合格数学新教师扎实掌握数学基本功底是前提．传讲理论知识，首先保证正确自然是重中之重的．从学生到教师角色的转换，从讲台下写题到讲台上板书的转换，常常使得新教师们倍感不适，压力和紧张对教师们熟练掌握基础理论知识和思想方法提出了更高的要求．重视学科基础，夯实基本功底，加强思维考查是《数学学科知识与教学能力》不变的底色，对于《考纲》要求的学科知识全面深入的考查是自2011年国考教师资格项目启动以来始终坚持的原则，并且进一步加强基础知识和基本思想方法的考查向纵深延展是新时代展现的新趋势．

师者授业，一名合格数学新教师深刻领会大学数学与中学数学的联系是关键．传授思想，不仅需要教师扎实的功底，更需要教师能理清大学数学与中学数学的联系．站在高观点下看初等数学问题是更好开展教学实践工作的关键环节，能更好地帮助学生深入掌握中学数学的基本概念，能更好地引领学生深入掌握数学的思想方法，学会数学式思考．深刻领会两者间的联系是高观点看问题的基础，不能理清联系，没有系统掌握中学知识体系，不利于将来快速适应教学工作．深刻领会两者间的联系也是对高站位、深理解的深化．选取与中学数学联系紧密的大学数学基础知识，加强大学数学的考查，强调初等、高等数学间的联系是数学“学科知识”模块的重点，更是贯穿整个《数学学科知识与教学能力》试卷的考查重点．

师者解惑，一名合格数学新教师强化培养数学基本能力和综合应用能力是核心．答疑解惑，贯穿在数学教学活动的始终，能帮助学生进一步掌握知识，理解内涵，领会思想，应用提升，促进思维和能力的发展．如何做到答疑清楚明白、通俗易懂、启发思考、激发兴趣？扎实基础是前提，高站位下领会中学与大学数学联系是关键，而最核心的是教师自身强大的数学基本能力和综合应用能力，这需要十几年数学学习和训练的积累和沉淀．数学教学的核心目标是培养学生的数学能力，而教师作为塑造人的人，对自身数学能力的培养提出更高的要求．数学“学科知识”的试题通常考核考生的多种能力，坚持专业化导向，突出能力考查，要求考生同时应用多种能力分析并解决问题．

2 中学数学教师资格考试“学科知识”结构特点

2.1 试题结构比例

《考纲》中对于“学科知识”模块试卷结构的规定见表2[2]．

表2 《数学学科知识与教学能力》科目试卷结构（局部）

《数学学科知识与教学能力》科目满分150分，其中《考纲》要求“学科知识”模块赋分比例约为41%，即有61分的题目考查学科知识．其中客观题单项选择题，题分为30分；主观题分为简答题和解答题，题分31分．选择题主要考查数学基础概念、定理、公式、法则的掌握情况．简答题要求考生简要写出解题思路和过程，主要考查其应用知识和方法分析解决问题的能力．解答题要求考生详细写出解答过程，能较全面反映其数学基本能力和综合应用能力水平，展示分析问题并综合应用数学知识进行逻辑推理的过程，是“学科知识”模块单题分数最高的题型[4]．

2.2 试题考查知识比例

根据《考纲》要求，将“学科知识”部分又进一步细分成“分析”“代数”“几何”“概率统计”4个分项（见图1）．通过对近7年笔试试卷“学科知识”模块总计140道试题进行逐一分类统计，发现初级中学“学科知识”模块中，“分析”分项考查分值占比最高达38.29%，即61分考查试题中平均约有23.4分的题目考查了“分析”分项内容；“代数”分项占比为28.57%，再次为“几何”分项，占比为19.91%，占比最低为“概率统计”分项，为13.23%．高级中学“学科知识”模块中略微增加了“代数”和“概率统计”分项的分值比重，4类分项的占比大小顺序仍与初中保持一致，详见表3．由于方程、函数作为中学数学内容最多、难度最大、贯穿始终的核心基础知识，同时也是初等数学与高等数学联系最为紧密的内容，《数学学科知识与教学能力》在“学科知识”模块分数分配设置中“分析”分项占比>“代数”分项占比>“几何”分项占比>“概率统计”分项占比．这样知识分项的设计考查全面，突出重点，较为合理．

表3 “学科知识”模块各知识分项试题数和分值占比

2.3 试题考查能力比例

根据《考纲》要求，突出能力导向，将主要考查考生的数学能力分为“运算求解”“分析判断”“推理论证”“抽象概括”“空间想象”“数据处理”“综合应用”7个侧面进行统计分析．由于一道试题可能考查考生多种能力，按照试题考查目标对各项能力侧重程度的不同，分别给每道试题按上述7个能力侧面进行打分，通过归一化处理获得每道试题在7个能力侧面上的权重分数．共分析了近7年笔试试题，得到各项能力侧面分值平均占比（见表4）．发现对于考生“运算求解”能力是考查最为突出的一方面．“会根据法则、公式进行正确运算、变形和数据处理，能根据问题的条件寻找与设计合理、简捷的运算途径，能根据要求对数据进行估计和近似计算”[6]，这是作为一名数学教师最基本的能力．对于报考初中学段考生而言，“分析判断”能力是第二大能力考查项，“分析判断”能力主要体现在考生对于基本概念、性质、定理、命题的理解和掌握上，通过已掌握的知识去分析判断命题对错，理清命题中的充分条件和必要条件，将问题化繁为简抓住事物本质，在考查题型上主要集中在客观题中，反映了对于初中段考生而言，重点考查他们对概念的理解程度，要求知其然．对于高中段考生来说，赋分平均占比第二高的是“推理论证”能力，主要集中在主观题上，要求考生能详细的写出推导过程，重点考查他们对公式、定理、数学思想的掌握和运用程度，要求知其所以然．这种赋分占比的差异化，充分考虑了初高中考生群体层次的差异和未来承担教学任务的要求不同，体现了命题组以人为本的精神．除“运算求解”“数据处理”能力外，其余5种能力考查赋分占比较为平均，再次说明试题在能力侧面的考查上突出重点，考查全面，赋分合理．

表4 “学科知识”模块试题中7种能力考查分值平均占比（%）

3 中学数学教师资格考试“学科知识”考情分析

3.1 各题型得分情况

通过对笔试试题按题型进行分类统计分析（见图2）．从考生群体角度看，报考高中学段的考生在各类题型的得分率上均高于报考初中学段的考生，且各类题型高中得分率比初中高出近12%．由于考生群体差异，报考高中学段的考生在学历层次、学校层次、知识水平上普遍高于报考初中学段考生，这样的得分率之差是合理的．从试题质量的角度看，“单项选择题得分率”>“简答题得分率”>“解答题得分率”，这符合《考纲》要求和题型难度特点，同时初级中学《数学》试卷设计难度低于高级中学《数学》试卷设计难度，初级中学和高级中学不同考生群体在不同题型上的得分率均落在合理区间，没有偏题怪题，具有较高的信度，展现了较为科学、高质量的命题水准．

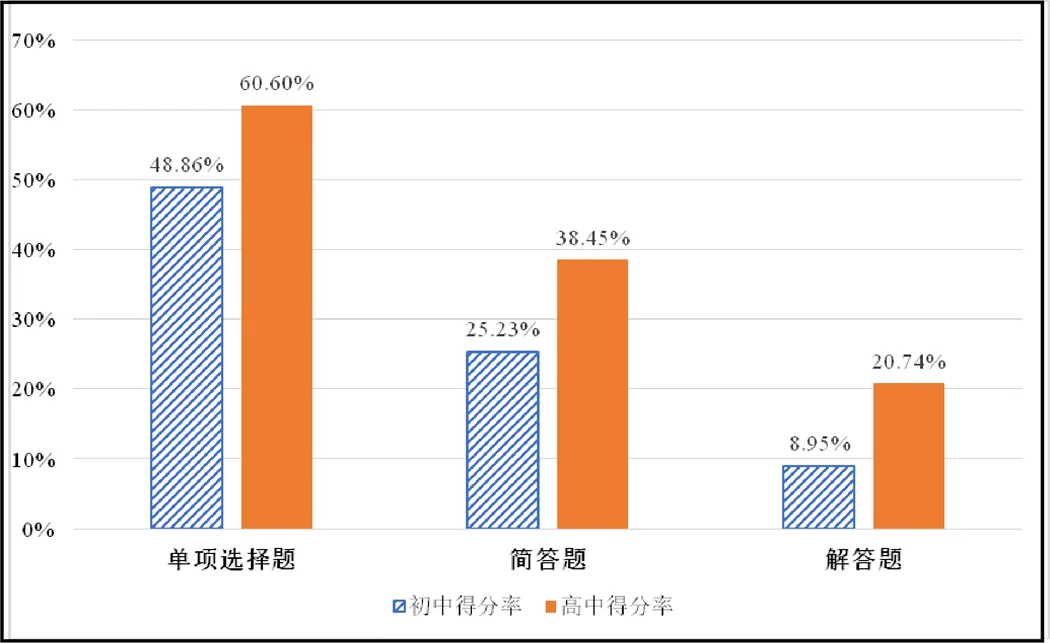
图2 近7年考试数学“学科知识”模块各题型平均得分率

3.2 各知识分项得分情况

通过对笔试试题按知识分项进行分类统计分析（见图3）．从考生群体角度看，由于报考高中学段的考生能力水平普遍高于报考初中学段的考生，故在各知识分项的得分率上，高中均比初中高出了十多个百分点．

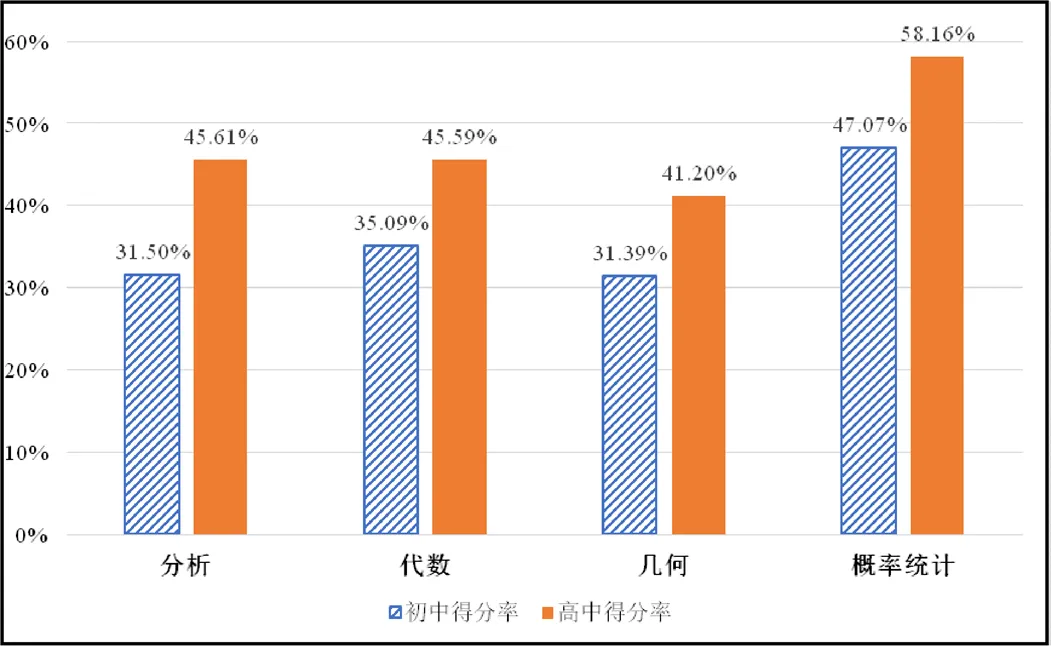
图3 近7年考试数学“学科知识”模块各知识分项平均得分率

从试题质量角度看，各知识分项的平均难度均能落在[0.3, 0.7]之间，难度合宜，具有较好的区分度，各分项设置的考查分数占比也较为科学合理，历年的分项分数分配和难度设计都较为平稳，保证了国家考试的严肃性，7年来始终保持高质量的命题水准．

从各知识分项的角度看，“几何”分项的得分率最低，这主要可能由以下几方面因素造成：第一，在几何分项的题目中，大多数题目主要集中在大学《解析几何》这一块．而《解析几何》知识点较为零碎分散，公式较多，大多数考生对于《解析几何》的知识仍处于了解阶段，不能弄清公式的来龙去脉，没有较为扎实地理解掌握；第二，《解析几何》主要是大一上学期的课程，同时《解析几何》相较于《数学分析》《高等代数》来说，与大部分高年级专业课的联系较少，所以对于大三年级及以上在校生群体和非在校生群体而言，相隔时间较为久远，对知识点遗忘较多；第三，几何分项的题目，对于考生的空间想象能力要求较高，在向量方法引入立体几何后，考生群体从中学段起对于空间想象能力的训练整体被削弱，使得考生普遍对于空间曲线、曲面的想象和处理上存在困难，导致几何分项得分较低．而“概率统计”分项得分率最高，但这并不能说明考生在这一块掌握较好．造成“概率统计”得分率偏高的原因，一方面是因为这一块的试题数量较少，考查分数占比初高中均只有13%；另一方面，这一块的试题在考点选取上主要集中在中学课程中的古典概型、几何概型等内容，知识点较容易理解掌握，考生普遍得分较高．但凡是“概率统计”涉及到大学课程的内容，得分率往往较低．以2018年下半年解答题第14题为例，该题主要考查随机变量的数字特征和分布，非常常规的题目，考点属于《概率论与数理统计》重要核心知识点，而初中段剔除零分卷后的有效均分仅为0.64（该题满分10分），而高中段有效均分仅为1.98，得分率均低于20%．总体而言，初高中各知识分项得分率整体偏低，考生整体在学科知识掌握上不尽如人意．

3.3 各能力侧面得分情况

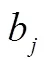
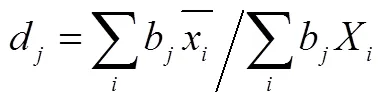
进而大致可以反映出考生群体在不同能力侧面上表现的水平高低，或者大致反映试题对于整个考生群体而言在该能力侧面上考查的相对难易程度．

通过对近7年笔试试题各能力侧面得分情况进行分类统计（见图4）可知，整个考生群体在“数据处理”能力、“分析判断”能力上有较好的表现，而“抽象概括”能力、“运算求解”能力、“空间想象”能力有待提高．

“综合应用”能力，在“学科知识”模块主要表现在考生对于多知识点复杂问题的综合分析处理上，要求考生有扎实的基础知识功底，深入理解不同知识间的联系并能灵活运用．考查“综合应用”能力的试题主要集中在主观题，具有较好的区分度．高中段在“综合应用”能力上表现尚可，而初中段在“综合应用”能力上需要努力提高．

“推理论证”能力，对考生要求普遍较高，需要有深厚的数学功底和数学专业背景，能较好地区分数学系和非数学系考生．该项能力对于报考初高中段考生群体都比较有难度，尤其对初中学段区分度较低．但由于高中段教师需要更高的理论要求，对于高中学段的考生来说需要加深对事物本质的理解，抓住核心思想，进一步提升自身“推理论证”能力．对于初中试卷来说，可以考虑适当再进一步减少初级中学“推理论证”题目的赋分比例，或选取相对难度更低一些的知识点来考查“推理论证”能力．

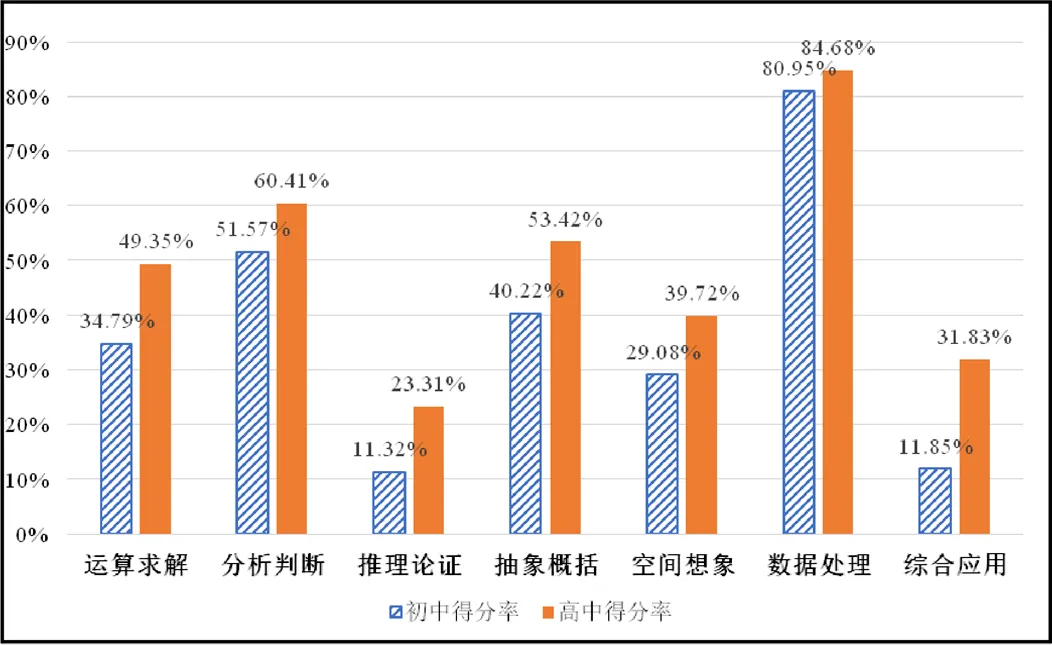
图4 近7年考试数学“学科知识”模块各能力侧面得分情况

3.4 师范生与非师范生考情对比

为响应中共中央国务院4号文件精神，为师范院校培养质量提升提供数据支撑，以期不断提升数学教师专业素养，尤其是数学师范生专业素养．为进一步细化考试群体分析，选取2015年下半年至2019年上半年8次考试“学科知识”模块总计80道试题分师范生群体和非师范生群体分别进行统计分析．发现初中学段师范生在数学“学科知识”模块近4年8次考试的平均得分率为31.92%，非师范生平均得分率为30.01%，师范生比非师范生平均得分率高出1.91%；高中学段师范生在数学“学科知识”模块近4年8次考试的平均得分率为44.75%，非师范生平均得分率为41.08%，师范生比非师范生平均得分率高出3.67%．师范生整体在数学“学科知识”模块的得分率优于非师范生，这主要是因为师范生考生群体还是以数学专业或数学教育专业的学生为主，受过专业数学基础学科的训练[4，7]．也反映试题所强调的专业化导向，较好地体现了考查目标，具有较高的信度和效度．

具体到知识分项，分师范、非师范群体，分别分析近8次笔试试卷数学“学科知识”模块的得分情况，参见图5．从时间维度纵向看，相较于图3汇总的近7年笔试试题各分项平均得分率，2015年下半年起近8次考试初高中学段在“学科知识”各个分项上的得分率均略有所下降，这主要是因为试点省份的扩大，考生人数的爆发增长，考生整体平均水平略有下降导致．仅2015年下半年当次考试就新增6个省份加入试点，而近4年共新增14个省份，其中江浙沪等教育发达地区早在2015年以前就已加入试点[7]．从知识分项角度看，师范生在各个分项的得分率均高于同学段的非师范生，尤其高中段师范生在“分析”“代数”“几何”上明显优于高中段非师范生．而学科“分析”分项平均得分率较其它分项较低的原因，主要是“分析”在主观题中考查较多，而主观题题型难度比客观题要高不少，同时选取“分析”考点在“推理论证”能力方面考查较多，这对考生来说又是难点．这也反映出命题对于“分析”分项的考查要求较高，而初高中学段考生在“分析”分项的掌握上还有待进一步提高．

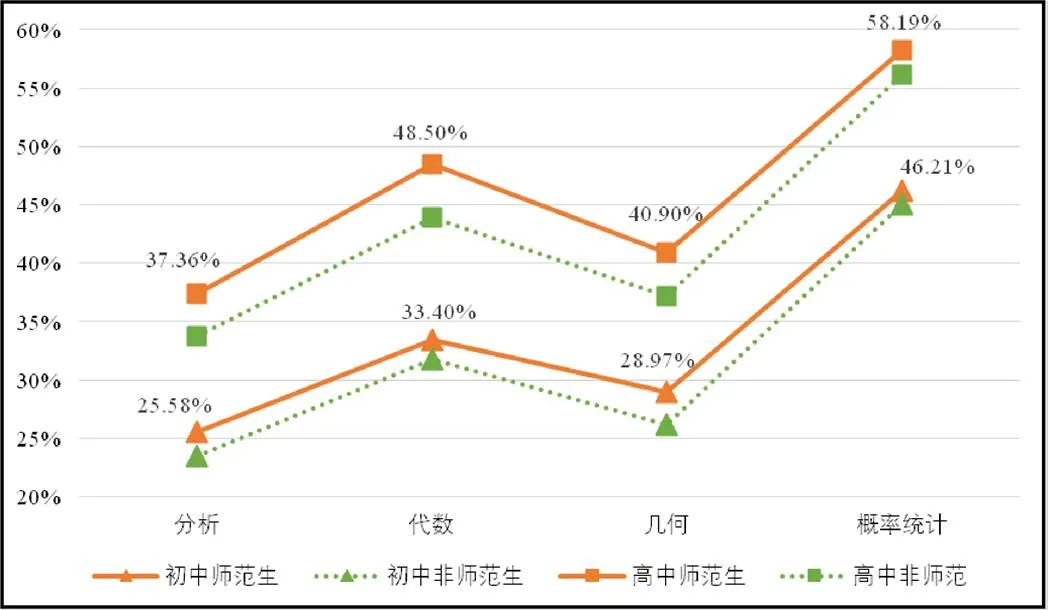
图5 近8次考试师范生与非师范生在数学“学科知识” 模块各分项平均得分率

具体到能力侧面，分师范、非师范群体，分别分析近8次考试笔试试卷数学“学科知识”模块的得分情况，参见图6、图7．初中段考生，师范生除“综合应用”能力的得分上比非师范生略低以外，其它各方面均略高于非师范生；高中段考生，师范生在7个能力侧面上表现均优于非师范生，尤其在“运算求解”“分析判断”“推理论证”方面明显优于非师范生．

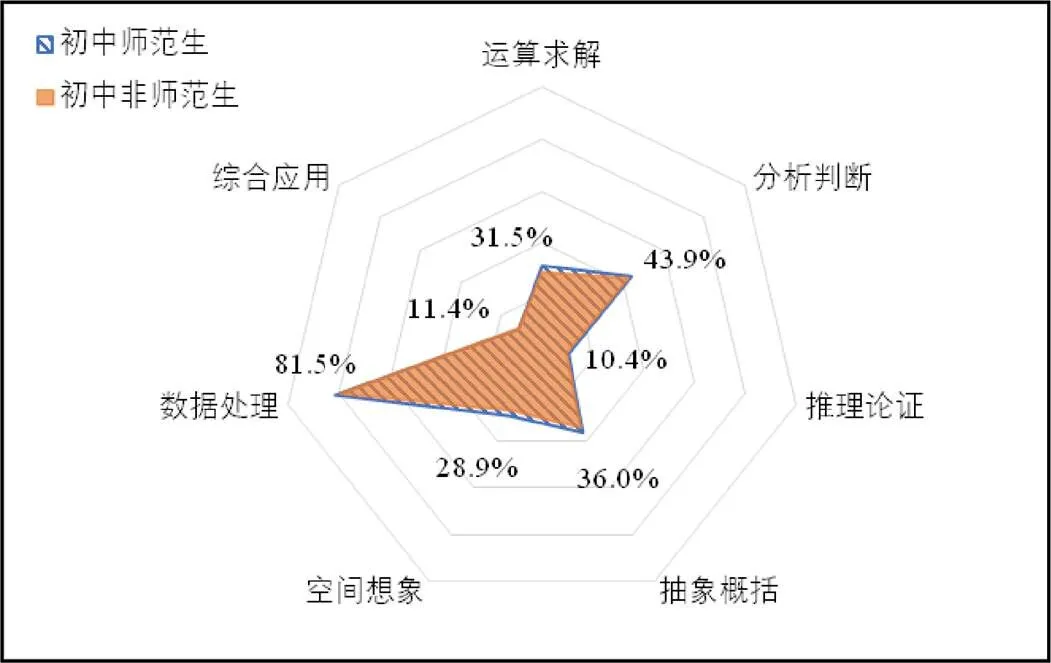
图6 近8次考试初中段师范生与非师范生在数学“学科 知识”模块各能力得分情况

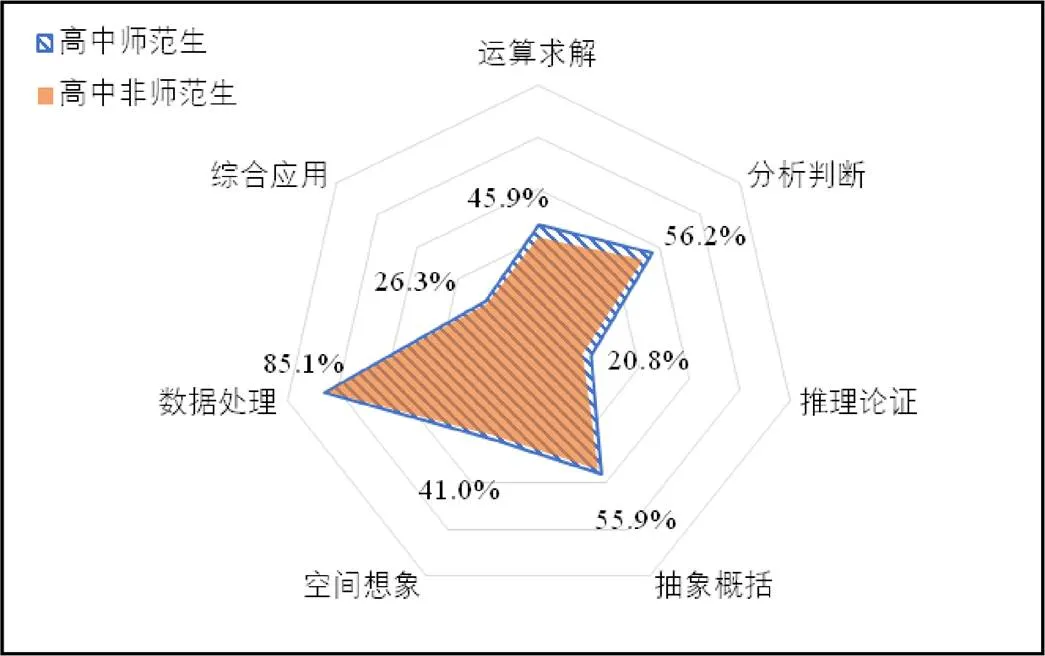
图7 近8次考试高中段师范生与非师范生在数学“学科 知识”模块各能力得分情况

4 总结与展望

百年大计，教育为本；教育大计，教师为本．为深入贯彻落实党的十九大精神，造就党和人民满意的高素质专业化创新型数学教师队伍．实行中小学教师资格的国家统一考试，增加科目三的考查，提升准入门槛，是深化教师制度改革的重要举措，是实现教师专业化的有效途径，为推动教师教育质量的提升起到关键作用．一名合格数学新教师扎实掌握数学基本功底是前提，深刻领会大学数学与中学数学的联系是关键，强化培养数学基本能力和综合应用能力是核心．《数学学科知识与教学能力》在“学科知识”模块，牢牢把握“夯实学科基础，突出能力考查”的原则，以育人导向为根，以能力导向为本，以专业化导向为核心，以实践导向为基础．紧扣时代发展，不断适应新时代教师队伍建设的新要求．

国家教师资格考试截至2019年上半年，共举办16次笔试，16次面试，已经积累了大量的数据和较为丰富的经验．对过去已考试题进行深入研究和数据分析，对于进一步推动国家教师资格考试制度的完善，考试大纲的修改，提高职前新教师专业化水平，提升中小学教师队伍质量有重要意义．从《数学学科知识与教学能力》“学科知识”模块切入，统计分析了近14次考试的试卷和考情数据．从试卷质量上看，试题结构合理，赋分分配合宜，难度均落在合理区间，没有偏题怪题；试题紧扣考试大纲要求，突出学科特色，重点考查“分析”分项、“代数”分项，重视考生的“运算求解”能力，侧重初中段“分析判断”能力和高中段“推理论证”能力，考查全面、重点突出，体现“4个导向”，充分考虑了初高中考生群体差异，彰显以人为本精神，具有较高的信度和效度，为国家选拔合格的数学新教师奠定坚实基础．从考生考情上看，高中段教师考生在各题型、各知识分项、各能力侧面上的表现全面优于初中段教师考生；师范生同样在各个方面优于非师范生，这也再次体现了试题具有较高的区分功能，较好地达到了考查目标，效度较高；考生整体在“分析”“几何”分项上表现不佳，在“空间想象”能力、“综合应用”能力、“推理论证”能力上有待提升．

有研究显示，学生数学学科知识与数学教育理论知识和数学教育实践知识都有显著的正相关[9]．也有研究通过概化理论，发现教师资格考试中学数学试卷中学科知识模块的测量精度较高，并且学科知识部分的题目在区分考生能力上的功能最好[10]．扎实掌握数学学科知识，是成为一名合格数学教师的前提．从目前的数据来看，考生整体在数学学科知识的掌握和应用上还需进一步提高．未来数学在“学科知识”模块将进一步重视公式、定理的理论推导，加强对基础知识的深入理解与综合应用，拓宽对基础知识的多角度理解，深化中学数学与大学数学间的联系．坚决反对教育机构为考试而教，甚至只教重点考查科目，对于不考少考考点一笔带过．这也对考试提出更高的要求，加大试题创新，加强综合考查，加深测评研究，为国家真正选拔出学得广、学得深、学得扎实的高素质专业化数学教师而努力奋斗．

[1] 中共中央国务院．关于全面深化新时代教师队伍建设改革的意见[EB/OL]．（2018–01–20）[2019–08–20]．http:// www.moe.gov.cn/jyb_xwfb/moe_1946/fj_2018/201801/t20180131_326148.html．

[2] 郑晨，李淑文．中国数学教师学科知识研究的现状与展望[J]．数学教育学报，2018，27（4）：62–67．

[3] 中华人民共和国教育部．中小学教师资格考试（笔试）大纲（试行）[EB/OL]．（2019–02–28）[2019–08–20]．http://ntce.neea.edu.cn/html1/report/1508/347-1.htm．

[4] 赵轩．注重能力考查 推动专业化建设[J]．数学教育学报，2016，25（6）：7–9．

[5] 刘晓玫．中学数学教学研究[M]．北京：教育科学出版社，2016：20．

[6] 教育部考试中心．2019年普通高等学校招生全国统一考试大纲（理科数学）[EB/OL]．（2019–01–31）[2019–08–20]．http://gaokao.neea.edu.cn/html1/report/19012/5965-1.htm．

[7] 教育部考试中心．中小学教师资格考试师范生考试情况报告（内容材料）[R]．北京，2017．

[8] 教育部考试中心．中小学教师资格考试统计分析报告（内容材料）[R]．北京，2019．

[9] 胡典顺，李东，朱龙，等．对教师资格考试的调查与建议——以“数学学科知识与教学能力（高级中学）考试”为例[J]．数学教育学报，2018，27（5）：77–82．

[10] 赵轩．基于多元概化理论的中小学教师资格考试数学学科试卷质量分析[J]．数学教育学报，2018，27（2）：38–40，102．

Consolidating Mathematical Foundations and Emphasizing the Assessment of Abilities to Facilitate Teacher Development——Investigating Future Teachers’ Mathematical Content Knowledge and Teaching Ability using the “Mathematics Knowledge” Module in the NTCE

LUO Cheng-yu

(National Education Examinations Authority, Beijing 100084, China)

Improving the quality of tests and promoting the cultivation of teachers through an empirical study of the National Teacher Certificate Examination (NTCE) is of great significance. A total of 14 exams from the second half of 2012 to the first half of 2019 were analyzed, and we will illustrate the test quality and examinees’ mathematical content knowledge through an assessment of content knowledge, the test structure, and the examinees. Regarding the quality of the test, the mathematics knowledge test module had a reasonable structure, moderate difficulty, high reliability, and validity. Regarding the examinees, the performance of high school teacher candidates was better than the performance of teachers who were junior school candidates, and the examinees who were students of normal universities had higher performance than the others. Because mathematics knowledge is the foundation of teacher professional development, examinees must further improve their mastery and application of mathematics knowledge. In addition, NTCE should focus more on mathematics knowledge in the future to consolidate the basis of mathematics.

mathematical content knowledge; high school teacher candidate; test structure; examinee; teacher professional development

G424.74

A

1004–9894（2020）03–0051–06

2019–12–21

国家教育考试科研规划课题——我国中小学教师资格考试命题理念及其实践研究（GJK2017016）

罗成禹（1992—），男，湖北宜昌人，研究实习员，硕士，主要从事考试研究与教师专业发展研究．

罗成禹．夯实学科基础 突出能力考查 打造高素质教师队伍——中小学教师资格考试数学学科知识与教学能力“学科知识”模块考情分析与测评[J]．数学教育学报，2020，29（3）：51-56．

[责任编校：周学智、陈隽]