多腔体气动软体致动器的建模与仿真
徐齐平, 刘锦阳
(上海交通大学 船舶海洋与建筑工程学院, 上海 200240)
与通常用于特定环境下重复作业的传统刚性机器人不同,软体机器人因其变形量大、安全性高、柔顺性好、自适应性强、与环境相容性好等优点而逐渐涌现并受到很高的关注度.软体机器人是一种以自然界的柔软体生物为原型的新型连续体仿生机器人,是机器人研究领域的拓展,其利用诸如硅胶、水凝胶、橡胶、电活性聚合物等柔软性材料制成[1-3],可以实现抓取、爬行、游动、弹跳等复杂运动[4-6].软体致动器可以广泛用于实现各种复杂精细动作,其由气压、加压液体、热、电场、化学反应等驱动.其中,气动软体致动器因输入简单、质轻、材料成本低和制造效率高等优势而具有广阔的应用前景[7-8].
在大量气动软体致动器的设计中,纤维增强型致动器[9]和气动网络型致动器[10]是两种十分受青睐的类型.纤维增强型致动器主要由具有整体腔室的弹性体、螺旋排列的纤维和不可延伸层构成.通过改变纤维角度,可以实现伸缩、扩展和弯曲等动作.气动网络型致动器由多个相互连接的、网络状的腔室构成[11],通过在腔室内部施加气压,使致动器充气膨胀,实现预定的弯曲变形,执行各种基本动作.
气动软体致动器除了能够完成平面内的基本运动形式之外,还可以实现空间内的弯曲、扭转、螺旋等耦合运动以便进行灵活操作[12-13].哈佛大学的Whitesides及其团队[4, 11]设计制作了大量气动软体致动器并进行一系列实验,这些致动器可以执行许多动作,从而完成移动、爬行、游动、弹跳等复杂运动.Hirai等[14]提出一种分析模型并使用可变形圆柱型致动器以展现这些运动形式,并利用由多个单弹性管组成的一组气动致动器实现复合运动.Moser等[15]应用一种分析模型,通过平行组合纤维和采用额外的纤维创建了蛇状致动器.Connolly等[3, 9]详细分析了纤维增强型致动器的运动如何受到纤维角度的影响,并提出了快速设计的分析模型.Sun等[16]提出了一种通过周向改变气动软体致动器的应变约束层的每个步骤,以实现螺旋运动的方法.
虽然国内外学者在气动软体致动器的设计方面开展了卓有成效的工作,但是如何对其建立准确的力学模型,并且采用何种方法是行之有效的,这仍是个具有挑战性的难题.有限元思想提供了一种切实可行的解决途径,考虑到软体致动器的材料和几何非线性,为了降低计算成本、揭示物理现象、满足精度并提高效率,需要选择合适的单元类型和非线性本构关系.针对经典位移场型的实体单元,高阶单元通常比低阶单元更精确有效,然而从计算效率来看,高阶单元难以应用于实际场合,因为其难以构造且计算更耗时,尤其对于自由度庞大和几何构型复杂的三维软体结构更是如此,因此,在保证计算精度的前提下,采用低阶单元更加高效.此外,在计算单元内力阵和刚度阵时,如果采用完全积分法,会出现体积锁定现象.为了避免体积锁定问题且保证计算效率,采用选择性缩减积分技术以解决该问题.综上所述,采用缩减积分法的低阶实体单元对气动软体致动器进行建模是一种合理的解决方案.
上述软体致动器的共同之处在于它们具有气动网络构造,不可压缩超弹性体嵌入到一系列相互连接的气腔中.之前大部分研究主要集中在设计制作、实验及采用杆、梁等简单模型进行整体变形分析上[10, 17-18].相对而言,在考虑到相邻两气腔互相接触的情况下,对整个气动软体致动器进行建模与分析则很少涉及,然而这正是我们感兴趣和关注的地方.尽管以前的实验研究已经明显观察到软体致动器相邻两气腔彼此接触的现象,但仍缺乏关于相邻两气腔之间如何接触的研究.迄今为止,在考虑接触的情况下如何使致动器实现足够弯曲变形、建立准确的力学模型并进行整体构型和应力分布分析尚是一个未得到有效解决的难题.
本文针对多腔体气动软体致动器相邻两气腔之间的互相接触问题,考虑到结构的复杂性、材料和几何非线性,采用多点接触的面-面接触方法,对其进行建模与分析,解决了不考虑接触时相邻两气腔之间的穿透问题.仿真结果表明,接触对致动器的大变形影响显著.最后,对软体四爪机构抓取圆柱体的整个过程进行了准静态研究,详细阐述了整体构型和Mises应力变化,这有助于指导软体致动器的优化设计及力学特性研究.
1 气动软体致动器
图1所示为常见的内嵌4个气腔的气动软体致动器,制作过程详见文献[19].为了清楚地显示致动器的内部结构,考虑到结构的对称性及简化计算,首先以其一半作为研究对象,内部构造如图2所示.图1和图2中:L=44 mm,W=20 mm,W1=10 mm,H=13 mm,t=4 mm,t1=2 mm,t2=10 mm,t3=6 mm,t4=8 mm.

图1 气动软体致动器

图2 气动软体致动器的一半
2 建模及非线性力阵
采用能够消除体积锁定的、具有选择性缩减积分的三维实体单元进行建模,该单元所有场变量依赖于总体坐标x、y、z.实体单元在空间中具有任意的几何构型、材料属性和边界条件,其形状可以为平面或曲面的四面体或六面体.实体单元的每个节点具有3个移动自由度,从而可以在三维空间中实现任意变形.
对于三维实体单元,容易构造出形函数并进行数值积分,实体单元上任意一点的位移矢量在总体坐标系下的坐标阵为
u(ξ,η,ζ,t)=N(ξ,η,ζ)qe(t)
(1)

(2)
形函数对自然坐标与对笛卡尔坐标导数的转换关系为
(3)
式中:J为雅克比矩阵,可表示为
(4)

2.1 单元弹性力阵及其导数阵
设r为单元上任意一点的位置矢量,可表示为r=[xyz]T+u,定义G=[∂r/∂x∂r/∂y∂r/∂z]为变形梯度张量,G为变形梯度张量的行列式.右柯西-格林变形张量C=GTG,tr(C)为C的迹.
引入体积能量罚函数,超弹性不可压缩材料的非线性Yeoh模型的单元应变能为[20]
(5)
采用选择性缩减积分技术以消除体积锁定问题,则
(6)
式中:GC=G(ξC,ηC,ζC),C为单元的中心点;κ为不可压缩常数;C10,C20,C30为材料常数,通过拉伸试验确定[20].I1为右柯西-格林变形张量的第一不变量,可表示为
(7)
将式(6)对单元坐标阵qe求导,可得单元弹性力阵为
(8)
将式(6)代入式(8),则单元弹性力阵可表示为
(9)
单元弹性力阵的导数阵为Qek对qe的导数,即
(10)
2.2 单元压力阵及其导数阵
为了反映相邻两气腔之间的接触情况,首先需要求出作用于气动软体致动器的单元压力阵.气压所做虚功可表示为
(11)

(12)
(13)
2.3 单元接触力阵及其导数阵
之前对接触的研究大多集中于硬质材料,而对软体致动器的研究也只专注于整体变形,没有考虑到软体致动器相邻两气腔之间的互相接触,且整体构型和应力分析也很少涉及.本文不计相邻两气腔之间的摩擦,假设给定的接触点总是唯一地投射到任意表面,针对软材料的软接触问题,引入多点接触的面-面接触方法研究相邻两气腔之间的接触情况.多点接触的面-面接触方法是指一个从单元的多个高斯点投影到相应主单元上并与主单元的多个高斯点接触的方法.为了避免穿透并提高精度,采用4×4个高斯点,当接触刚度系数逐渐增大到一定值时,结果收敛.同时为了避免在每个时间步对任意两个单元进行穷举几何搜索,接触检测可分为全局检测和局部检测两个阶段,全局检测阶段消除了大部分组合,并且选择一系列单元对进行局部检测,文中采用的全局搜索法是层次包围盒算法[21].
接触分析中的接触对由主面和从面构成,如图3所示.设v为从面上的从节点,m为从节点v到主面上的最近投影点[22].R是从节点v的全局位置矢量,ρ为最近投影点m的全局位置矢量,相对位置矢量为rmv=R-ρ,nm为接触主面的法向量,
ρ=ρ(ξm,ηm)
(14)

图3 最近投影点
首先,构造如下函数:
(15)
然后,求最近投影点主要是求解式(16)的极小值问题
‖R-ρ‖=(R-ρ)·(R-ρ)→min
(16)
通过求解式(17)可得式(16)的解
(17)
rmv在接触力的单位法线方向nm上投影为
(18)
显然,当d>0时,从面上任意一点和主面上投影点受到的接触应力pv=pm=0;而当d<0时,穿透量δ=|d|.由罚函数法,从面上任意一点和主面上的投影点受到的接触应力为
pv=kδnm,pm=-kδnm
(19)
式中:k为接触刚度系数.从面和主面的单元接触力阵为
(20)
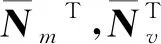
(21)
2.4 静平衡方程
针对图2所示一端夹持的多腔体气动软体致动器,可得具有约束的静平衡方程
(22)
式中:λ为约束方程对应的拉格朗日乘子列阵;Qk、Qp和Qc分别为系统总体广义弹性力阵、广义压力阵和广义接触力阵;Φq为雅克比矩阵;Φ=0为气动软体致动器受到固定端约束的约束方程.
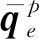
(23)
式中:nk为实体单元数;np为受气压作用的单元数;nc为接触单元对数.
综合使用Newton-Raphson迭代法和高斯积分法,对式(22)进行求解,在迭代计算中,第i步和第i+1步具有以下关系:
(24)
(25)
式中:Kk、Kp和Kc分别为Qk、Qp和Qk对总体广义坐标的导数阵,
(26)
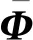
3 仿真分析、实验验证与模型比较
3.1 单个软体致动器的仿真分析
在考虑到相邻两气腔之间的互相接触情况下,通过求解式(22),采用多点接触的面-面接触方法,对图2所示一端夹持的多腔体气动软体致动器在受气压作用下的变形进行仿真分析,这里忽略重力的影响.
本数值算例的气动软体致动器的外形尺寸如图2所示,硅胶材料的各项参数如下:密度ρ=1 100 kg/m3,泊松比ν=0.499 5,Yeoh模型的材料系数C10=0.271 2 MPa,C20=0.030 53 MPa,C30=-4.013×10-4MPa,κ=1 000 MPa,接触刚度系数k=4 N/mm3.
为了清楚地观察到软体致动器气腔的内部变形和整体构型变化,按照1 mm的间隔对该致动器划分网格,当气压p=35 kPa时,在考虑接触与不考虑接触两种情况下,借助于MATLAB数值软件进行仿真对比分析,半个软体致动器的变形后构型分别如图4和5所示.图4为考虑接触时半个气动软体致动器的变形后构型,图5为不考虑接触时半个气动软体致动器的变形后构型.从图5可以看出在不考虑接触的情况下,相邻两气腔相互穿透,即图中黑色虚线包围的区域,这显然不符合实际情况;而在考虑接触的情况下,相邻两气腔互相接触,无穿透现象,这可以从图4明显地反映出.此外,为了清晰地显示软体致动器的相邻两气腔之间的应力分布,在考虑接触时对该致动器的Mises应力分布进行计算,Mises应力为
σs={[(σx-σy)2+(σy-σz)2+(σz-σx)2+
(27)
式中:σx、σy、σz分别为第一、第二、第三主应力;τxy、τyz、τzx为切应力.从而得出变形之后构型的 Mises 应力分布情况,如图6所示.
根据结构的对称性且考虑到相邻两气腔之间的互相接触作用,采用MATLAB软件对图1所示的整个多腔体气动软体致动器进行仿真,可得在气压p=35 kPa时变形后构型和Mises应力分布,分别如图7和图8所示.图7为考虑接触时整个气动软体致动器的变形后构型,图8为考虑接触时整个气动软体致动器的Mises应力分布情况.从图6和图8可以清晰地发现应力最大值位于相邻两气腔之间的接触区域与连接相邻两气腔的根部区域,这对气腔壁承受气压是个极大的考验,计算和分析这些区域的应力变化有助于软体致动器的优化设计和力学性能分析.

图4 考虑接触时半个软体致动器的变形后构型

图5 不考虑接触时半个软体致动器的变形后构型
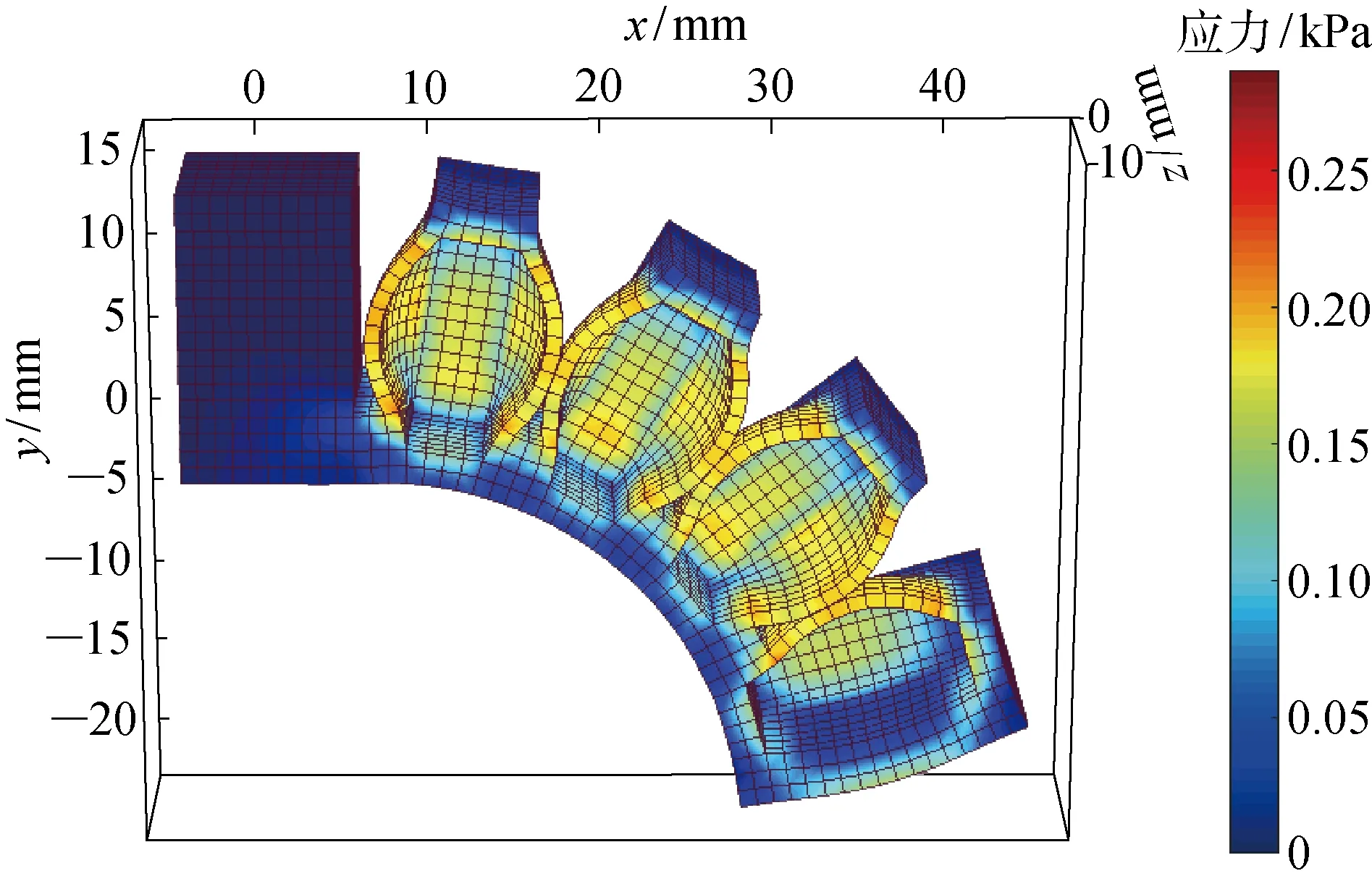
图6 考虑接触时半个软体致动器的Mises应力分布

图7 考虑接触时整个软体致动器的变形后构型

图8 考虑接触时整个软体致动器的Mises应力分布
3.2 实验验证与模型比较
为了验证所提出的多点接触的面-面接触模型对多腔体气动软体致动器建模的有效性和准确性,并测试该致动器受不同气压作用下的弯曲性能,对受不同气压载荷作用下的软体致动器进行相应的实验研究,得到其变形状态,如图9所示.从图9中可以清晰地看出,随着气压逐渐增大,软体致动器的变形逐渐变大,即固有曲率轮廓逐渐增大.
文献[10]采用杆模型对气动软体致动器进行研究,该模型基于弹性体的欧拉理论,即假定致动器的底层为弹性杆,是一种未强调相邻两气腔互相接触的简化模型.
图10给出了利用两种不同模型得到的加压气动软体致动器的变形形状.图中气压p依次取值为0,5,15,25,35 kPa.图中实线、虚线及离散点分别对应于利用多点接触的面-面接触模型获得的结果、杆模型获得的结果及实验数据,其中,实验数据可以通过测量图9中致动器上的各个黑色标记点的位置而获得.从图10中可以看出,软体致动器的变形随着气压增加而变大,当气压小于p=15 kPa时,即在小变形范围内,采用上述两种模型得到的仿真结果与实验数据基本一致.当气压大于p=25 kPa时,随着弹性变形逐渐增大,使用多点接触的面-面接触模型得到的结果与实验数据吻合,而使用杆模型得到的结果逐渐偏离实验数据,误差逐渐变大.这表明与杆模型相比,在大变形阶段,利用多点接触的面-面接触模型能够有效提高模拟大变形弯曲的精度.

图9 受不同气压载荷作用的软体致动器的变形状态
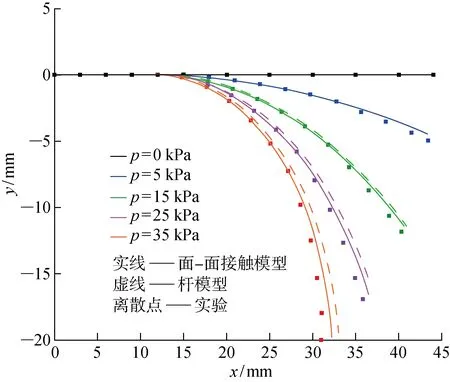
图10 利用两种不同模型得到的软体致动器的变形形状
3.3 软体四爪机构的仿真分析
利用3D打印技术制造一个装载气动软体致动器的平台,如图11(a)所示,具体尺寸为Lg=96 mm,l=34.5 mm,h=3 mm,h1=10 mm,h2=8 mm,w=27 mm,l1=23 mm,w1=20 mm,l2=20 mm,w2=17 mm,m=5 mm,其余各项参数与单个致动器的参数相同.
将图1所示的4个相同的气动软体致动器装载到图11(a)所示的平台中,组装成图11(b)所示的软体四爪机构.利用图11(b)所示的软体四爪机构对抓取圆柱体的整个过程进行准静态分析.软体四爪机构与圆柱体的位置关系如图12所示.
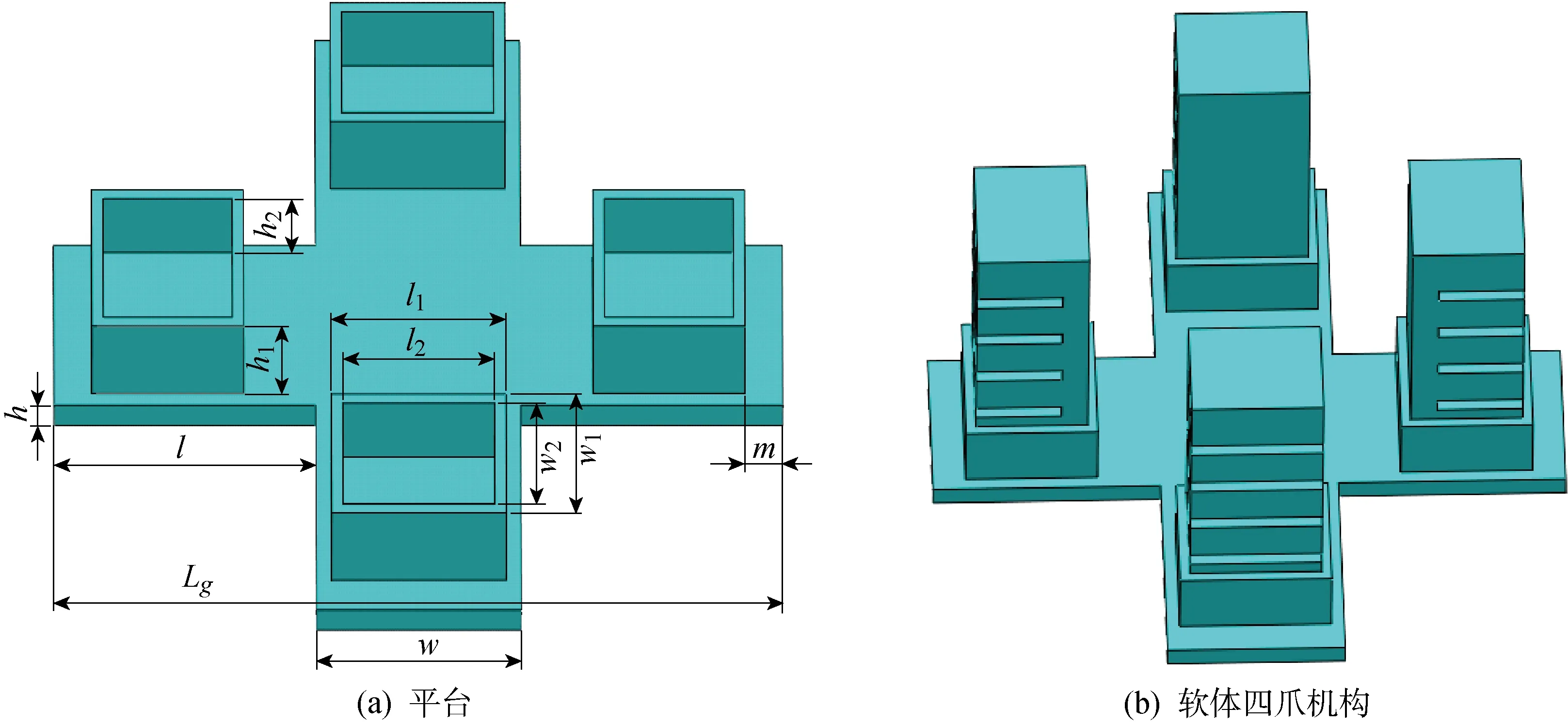
图11 平台和软体四爪机构
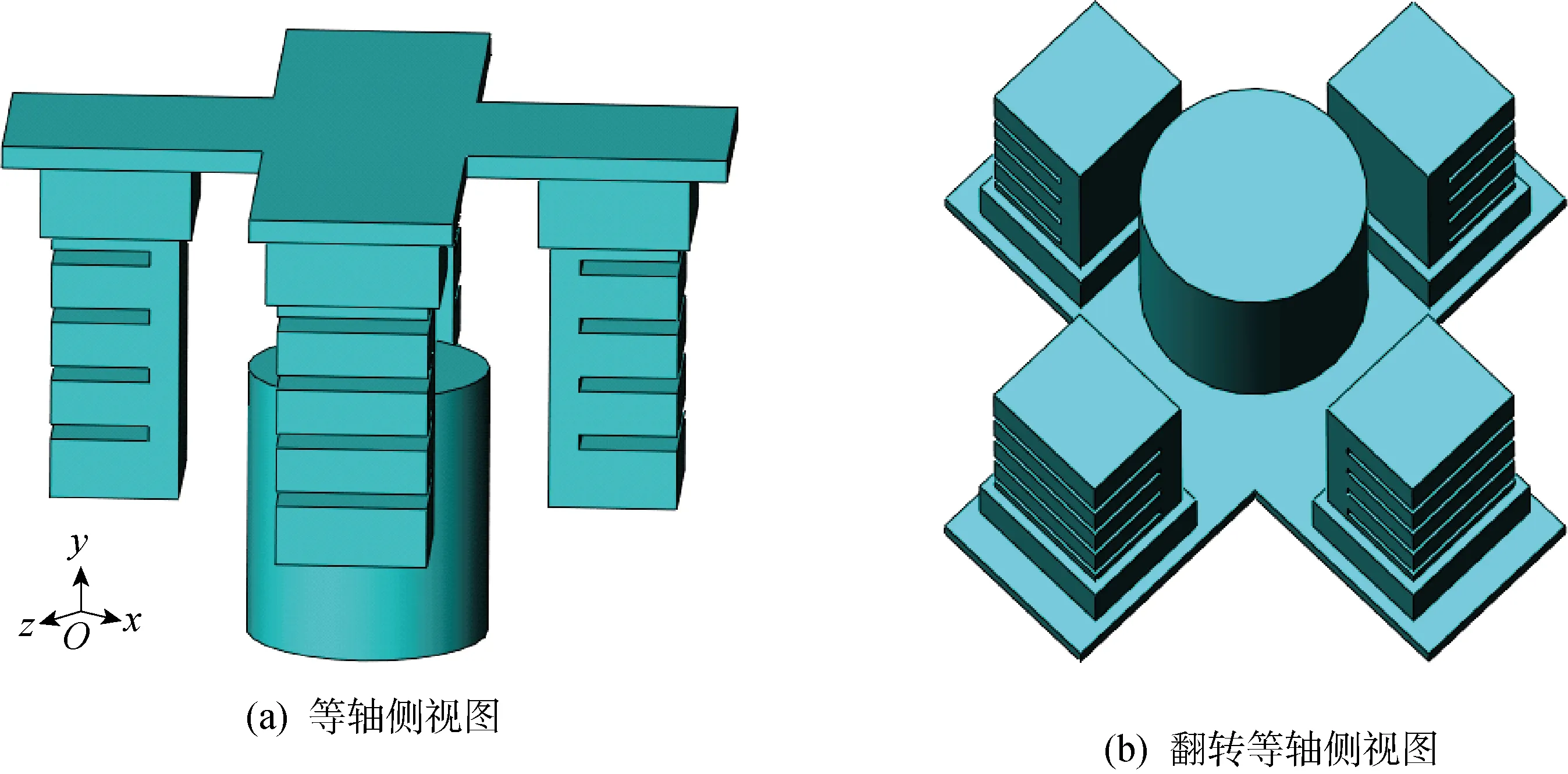
图12 抓取圆柱体的软体四爪机构
在分析了上述单个软体致动器之后,为了验证该致动器的性能,在考虑接触的情况下,采用多点接触的面-面接触模型对该软体四爪机构抓取圆柱体的整个过程进行准静态仿真分析.圆柱体的密度为 3 388 kg/m3,直径为32 mm,高为36 mm.初始时,软体四爪机构与圆柱体之间互不接触,圆柱体在支撑平台上处于静止状态.随后,该四爪机构的4个致动器开始均匀充气直到在t=1 s时达到35 kPa为止,之后保持该气压值不变,气压的加载曲线如图13所示.在t=2 s时,将支撑平台撤掉,在摩擦力作用下,圆柱体保持平衡.
考虑到结构的对称性,取四分之一圆柱体进行研究,软体四爪机构与圆柱体之间为点接触,如图14所示,这是机器人抓爪或人类手指抓取类型的最常见方式.
作用于四分之一圆柱体的力由带箭头的红色实线表示,法向接触力FN和摩擦力Ff必须满足以下静力学准则:
Ff≤μFN
(28)
式中:μ为静摩擦系数,取值为0.25.摩擦力Ff的大小为四分之一圆柱体的重力.
考虑摩擦力作用和位移约束,可得单个气动软体致动器的静平衡方程:

(29)
式中:Qg和Qf分别为系统总体广义重力阵和广义摩擦力阵;ΦN=0为软体致动器与圆柱体接触点的位移约束方程,λN为位移约束方程ΦN=0对应的拉格朗日乘子列阵.根据式(29),可以计算出几个时刻的法向接触力FN和摩擦力Ff的变化情况,如表1所示.
为了更具体和清晰地反映出软体四爪机构抓取圆柱体的整个准静态过程,绘制出其不同时刻的构型,如图15所示.
结合图13、图15和表1可知,在初始时刻t=0 s时,整个机构处于静止状态;在t=0.5 s时,软体四爪机构的4个致动器均匀充气膨胀产生弯曲变形而与圆柱体接触,法向接触力FN大于0,此时圆柱体还处在支撑平台上保持不动;在t=1 s时,充气气压达到最大值而使4个致动器与圆柱体紧紧接触,FN增大;直至t=2 s为止,圆柱体的重力与支撑力平衡而仍保持不动,摩擦力Ff的大小为0,FN保持不变.在t=3 s时,达到新平衡状态,FN和Ff满足平衡条件.

表1 法向接触力FN和摩擦力Ff
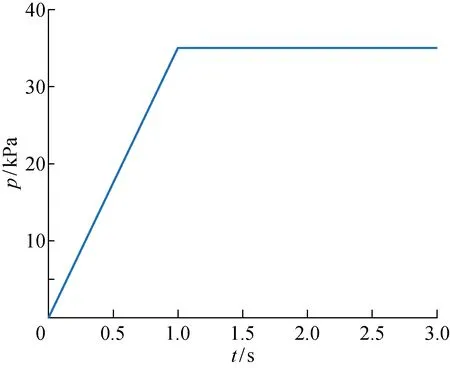
图13 气压载荷-时间曲线

图14 四分之一圆柱体
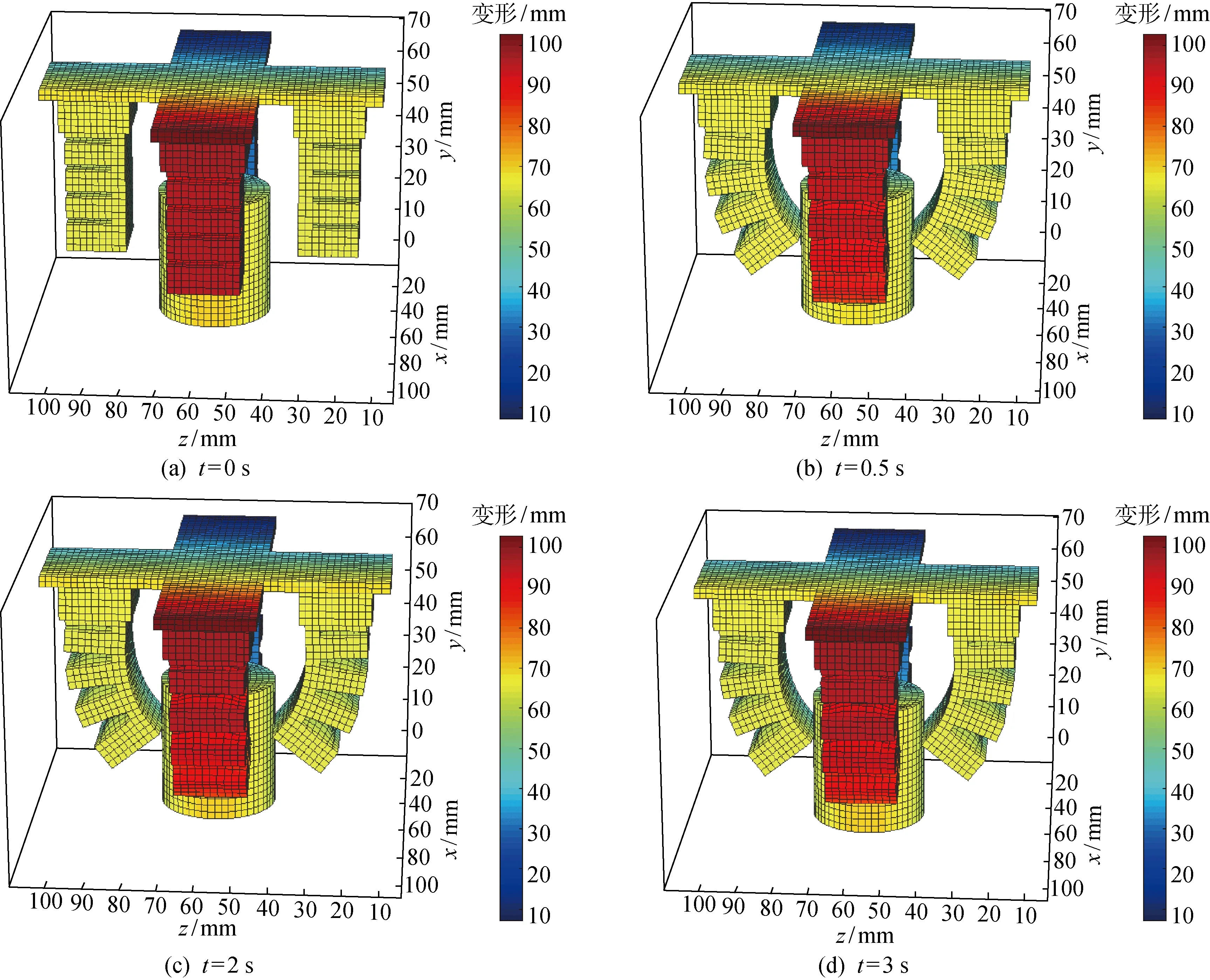
图15 在不同时刻软体四爪机构抓取圆柱体的构型
此外,为了显示软体四爪机构抓取圆柱体时的应力分布,根据式(27),可得未变形构型和变形后构型的Mises应力分布情况,如图16所示.由图16可知,在初始时刻t=0 s时,整个机构处于静止状态,其在未变形构型时的Mises应力分布为0;在t=3 s时,圆柱体在摩擦力作用下保持平衡,圆柱体与软体四爪机构之间的压力必须足够大,以满足摩擦力小于极限摩擦力.从颜色条可以看出相邻两气腔之间的接触区域Mises应力达到最大值,这个区域的应力变化情况特别值得注意,计算和分析这个区域的应力,有助于在不破坏气腔壁的前提下进一步优化设计软体致动器并分析力学特性.
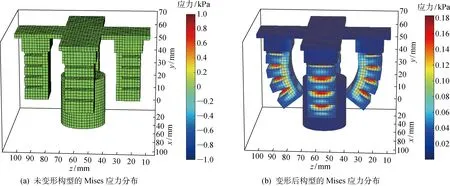
图16 软体四爪机构抓取圆柱体的Mises应力分布
4 结论
针对现有梁、杆等简单模型对气动软体致动器进行整体变形研究的局限性,且与刚性材料的硬接触不同,本文对多腔体气动软体致动器的软接触问题,建立了准确的力学模型,进行了整体构型和应力分布分析.综合考虑相邻两气腔之间的互相接触作用以及气腔结构的复杂性、材料和几何非线性,采用多点接触的面-面接触方法,解决了不考虑接触时相邻两气腔之间的相互穿透问题.通过相应的实验,验证了本模型的有效性,与杆模型相比,有效地提高了模拟大变形弯曲的精度.
本力学模型能够模拟在不同气压作用下软体致动器的弯曲变形,适用于研究各类致动器的大变形问题,不仅可以分析软体致动器的整体变形,而且能够描述气腔结构内部的应力分布情况.在考虑到相邻两气腔之间的互相接触时,能够准确地模拟其变形后构型;而在不考虑互相接触时,相邻两气腔相互穿透,这明显不符合实际情况.
软体四爪机构在变形过程中的整体构型和Mises应力变化揭示,相邻两气腔之间的接触对致动器的变形影响显著.相邻两气腔之间的接触区域为应力集中区域,如何在保证材料不屈服的条件下增大气压以实现成功抓取,是未来软体致动器设计需要考虑的一个重要问题.本文提出的力学模型对于气动软体致动器的力学特性分析、优化设计以及驱动性能研究具有一定的理论参考价值.

