多施翼无人机遥操机械臂多功能仿真实验平台的设计与实现

马仲航， 张执南

(上海交通大学 机械与动力工程学院， 上海 200240)

高空作业，如桥梁检修、风电机组维护具有较高的危险性.利用无人机(UAV)结合机械臂替代人工完成高空作业任务不仅可以大幅降低发生重大事故的风险，还具有广阔的市场应用空间.因此，无人机结合机械臂的研究获得了国内外的广泛关注[1].

目前，相关研究主要集中在空中抓取、空中搬运与空中遥操3个方面.虽然上述研究组成形式类似，但侧重点各有不同.空中抓取指无人机在动态飞行过程中，利用机械臂抓取特定目标[2]；空中搬运指利用单自由度的抓手或绳索实现目标物体的空中运输[3]；空中遥操指利用遥控方法控制无人机以及机载的多自由度手臂，进而实现空中特定任务的操作[4].空中遥操机械臂是基于空中遥操理念设计的六旋翼无人机和七自由度机械臂集成的空中机器人系统，通过分级控制将机械臂的运动作为无人机的外部扰动加以补偿，以实现复杂环境下无人机与多自由度机械臂的精细化操作.然而，为提高无人机遥操抓取的稳定性，还需设计和验证空中遥操机械臂的控制算法.

无人机控制算法验证是无人机试飞前最为重要的工作.仿真是验证无人机控制算法的主要方法.目前，大多数仿真验证方法主要利用MATLAB等软件进行数值仿真[5]，缺乏实时的可视化显示，无法直观地获取无人机的实时状态.本文基于Virtual Robot Experimentation Platform (V-REP)软件的二次开发，研制一套应用于多施翼无人机遥操机械臂的多功能仿真实验平台，实现对无人机-机械臂联合动力学的可视化仿真；提出一种基于质心实时采集的无人机增稳算法，在简化动力学模型的同时实现无人机对机械臂扰动的补偿；在抓取作业阶段，基于机器人逆运动学，实现机械臂对无人机扰动的隔离，高质量地完成增稳抓取任务.

1 空中遥操机械臂动力学模型构建

空中遥操机械臂采用分级控制策略来处理无人机与机械臂之间的扰动.基于该思路，首先研究七自由度机械臂的质心采集方法，将机械臂质心的变动作为机械臂对无人机的扰动，以简化空中遥操机械臂的动力学模型.

1.1 实时质心跟踪采集

七自由度机械臂的各臂节之间依靠转动副连接，由Hatenberg机器人位姿描述方法[6]，可获得每一臂节质心坐标系相对于世界坐标系的位姿关系.各臂节间的位姿转换矩阵如下[7]：

(1)

式中：βi为从xi-1到xi绕zi的旋转角；αi-1为从zi-1到zi绕xi-1的旋转角；di为从xi-1到xi沿zi方向的距离.动力链的位姿变换关系如下：

(2)

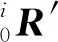
根据文献[7]的推导结果，多体系统质心求解的结果如下：

(3)

式中：xio、yio、zio分别表示第i链节质心相对于机器人基础坐标系的坐标；xcom、ycom、zcom分别表示多体系统的质心相对于机器人基础坐标系的坐标.需要指出的是，在下文的讨论中机器人基础坐标系即为无人机机体坐标系.

在V-REP软件中利用Lua语言编写脚本实现质心的跟踪功能.利用Threaded脚本的循环执行特性可以保证跟踪动力链质心的实时性，利用其提供的库函数可以降低编程实现的难度.该算法实现的流程图如图1所示.其中，调用V-REP库函数simGetShapeMassAndInertia()可实现对模型质量和转动惯量的获取；调用V-REP库函数simGetObjectPosition()可访问物体的空间位置；调用simGetObjectMatrix()可以获得任意两物体之间的位姿转换矩阵.多施翼无人机遥操机械臂实物及其仿真场景如图2所示.

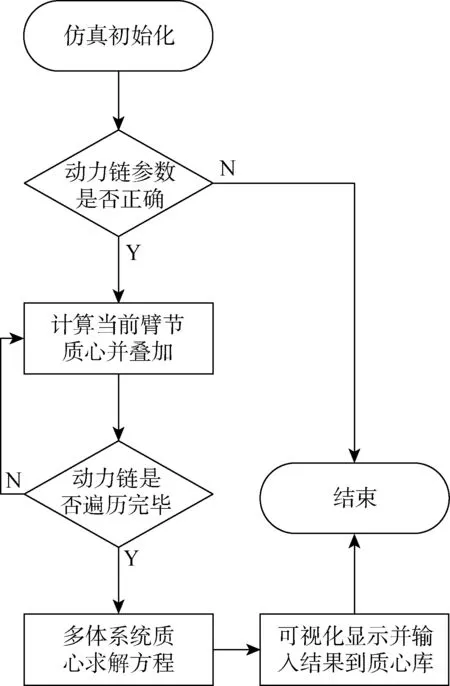
图1 质心跟踪算法框图

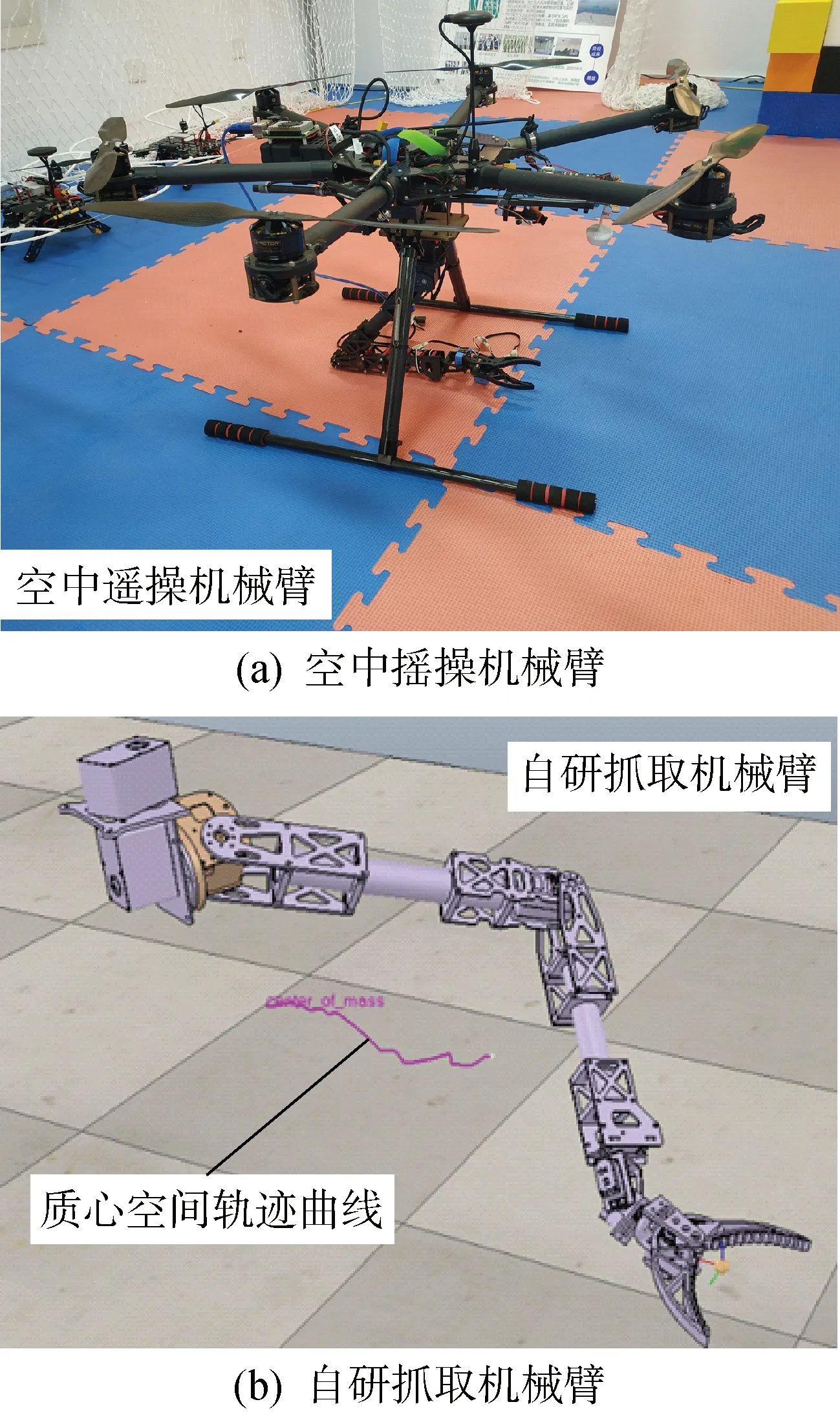
图2 质心位置实时跟踪显示

1.2 多施翼无人机遥操机械臂动力学模型

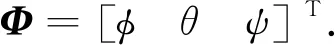
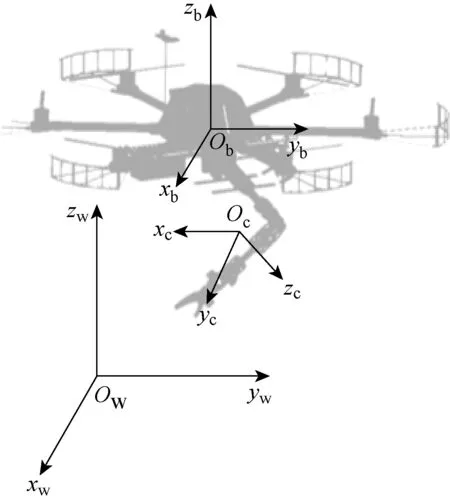
图3 空中遥操机械臂坐标系示意图

按所定义的Euler角顺序，可建立从机体坐标系至世界坐标系的转换矩阵R：

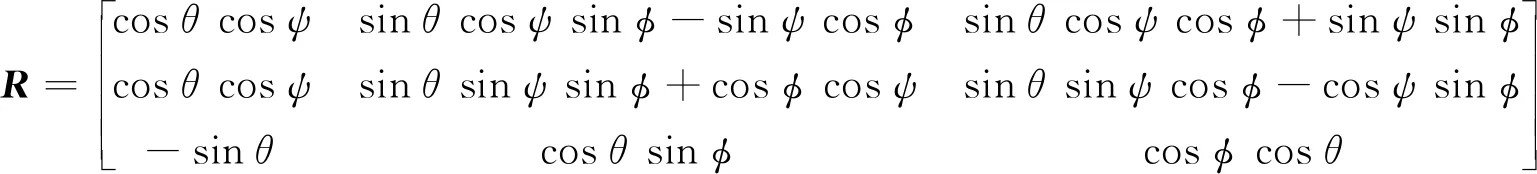
(4)

根据文献[8]，六旋翼无人机的每个螺旋桨均能产生升力Fi和力矩Mi，且均与转速γi有关，其关系式为

(5)

式中：kF为升力系数；kM为力矩系数.根据文献[9]，将无人机的总升力表示为在世界坐标系下沿坐标轴的分力:

(6)

式中：Bf为无人机在机体坐标系下的升力.定义向量m的3个分量分别代表沿机体坐标系的3个坐标轴方向的扭矩.

A=

(7)

式中：l为六旋翼无人机电机至机体质心的距离.由Newton第2定律可知

(8)

式中：mpla为无人机的质量；g为世界坐标系中的重力加速度；wez为世界坐标系中代表重力方向的单位向量.由Newton-Euler方程，在机体坐标系下有

(9)

式中：Jpla为六旋翼无人机的转动惯性矩阵.根据文献[10]，分析式(4)表达的转换矩阵R可建立无人机在机体坐标系下的角速度Bωpla和世界坐标系下的角速度wωpla之间的关系为

wωpla=RBωpla

(10)

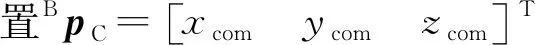
wpC=wppla+RBpC

(11)

由于遥操作业过程集中在无人机悬停的准静态阶段，针对该阶段，对机械臂的运动分析可以简化为对其质心的运动分析.根据文献[11]，机械臂质心在无人机机体坐标系下的绝对速度BvC为

(12)

式中：Bv为体轴系下三轴线速度.按文献[12]的约简方法，可由前文所推导的无人机动力学模型分析得出.将机械臂的重力变换至机体坐标系，并由Newton第2定律可得

(13)

式中：Cf为机体坐标系中机械臂对挂载点的作用力.由挂载点力矩平衡，则有

(14)

式中：BpL为挂载点在无人机机体坐标系中的位置向量.

2 基于质心采集的无人机增稳算法仿真实现

2.1 建模流程

在V-REP软件中，系统动力学模型的建立遵循以下流程[13]：① 导入STL格式的机械臂装配体；② 将导入的机械臂装配体拆分为单个零件，并将这些零件转化为物理引擎可识别的壳体；③ 对每个零件的壳体配置动力学参数；④ 按照相对位置关系配置关节、力传感器，形成动力链；⑤ 利用V-REP软件兼容的Lua语言编辑器编写嵌入式脚本，进行二次开发.

2.2 算法设计与实现

程序架构分为主程序和质心采集程序模块，其程序算法实现的流程图如图4所示.首先，利用simTubeOpen()建立V-REP软件内部各程序之间的通讯信道；然后，利用V-REP软件自带的Lua库函数，直接获得仿真场景中模型的动力学参数信息.利用simGetObjectVelocity()函数，获得无人机在惯性坐标系下的线速度wvC与角速度wωpla；利用simGetObjectPosition()函数，获得无人机在惯性坐标系下的位置信息wppla；利用simGetObjectOrientation()函数， 获得无人机在惯性坐标系下的位姿矩阵.按照这些信息求解方程组，以求得加载在无人机电机位置的力与扭矩.在世界坐标系下，利用simAddForceAndTorque()函数将所求得的力与扭矩施加在六旋翼无人机上.

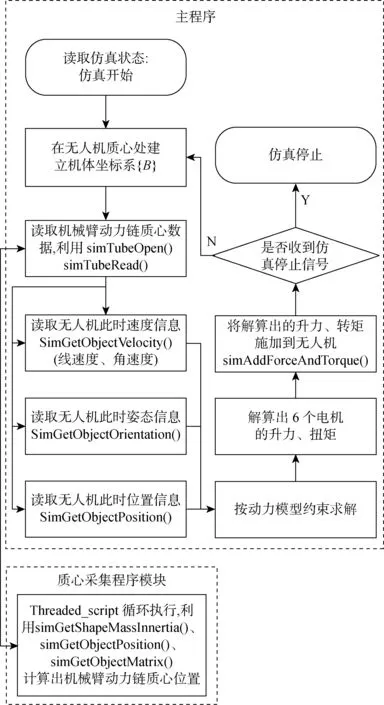
图4 基于质心采集的无人机增稳算法程序框图

图5 质心增稳算法效果对比图

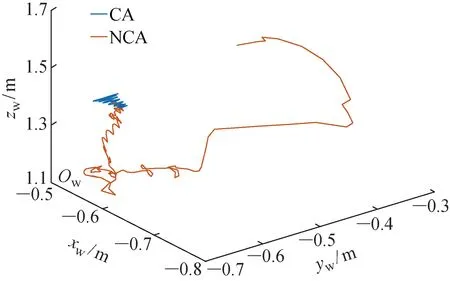
图6 应用质心增稳算法前后无人机的航迹对比图

2.3 仿真结果与对比

首先，在V-REP软件可视化仿真环境中进行直观地对比.在仿真开始后第5、7、9 s时刻分别截取是否应用基于质心采集的无人机增稳算法的场景图像，如图5所示.其中：CA代表应用质心增稳算法所获得的航迹；NCA代表未采用质心增稳算法所获得的航迹.然后，利用V-REP与MATLAB软件的联合仿真实现两种情况下无人机航迹的对比.利用Sockets包实现V-REP与MATLAB软件的实时通信，其航迹对比如图6所示.由图6可见，应用质心增稳算法后，无人机的飞行状态稳定，质心增稳算法效果显著.

3 多施翼无人机抓取增稳算法仿真实现

3.1 无人机定位误差对抓取操作的影响

分析无人机定位误差对机械臂抓取操作的影响，并提出一种简便方法以消除定位误差对抓取操作的干扰.

在室外作业环境下，受全球定位系统(GPS)的定位精度限制，机载电脑位置信息与真实情况存在误差[14].为简化问题，假设陀螺仪等姿态测量设备无误差.定义O1w为机载电脑中1号位姿的位置信息，rO1w为无人机真实位置信息；rt为目标物体的真实位置，t为目标物体在机载电脑中的位置.当无人机飞临工作区时，操作员遥操机械抓手靠近目标物体.根据机械臂转角信息可以确定目标物体与无人机的相对位置.当真实环境中无人机在风力作用下变为位姿2时，机载电脑中无人机根据姿态测量设备信息也做出相同的位姿变化，如图7所示.无论是实际情况还是机载电脑中的仿真情况，目标物体相对于无人机的位置关系一致，故无人机定位误差对抓取操作的影响可以通过操作员的操作方法消除.

图7 定位误差示意图

3.2 算法的设计与实现

空中抓取增稳算法实现流程如图8所示，其中DLS法表示阻尼最小二乘法.仿真开始，在无人机操作员发出悬停指令后，机载电脑读取此时无人机位姿信息与机械臂各关节转角信息.确定目标物体与机载坐标系的相对位置关系后，机载电脑循环读取陀螺仪和加速度计的信息，根据三轴平动、转动加速度积分确定位姿变化；接着，将动力链两端位置信息输入运动学逆解求解器，解算出七自由度机械臂各关节转角信息.至此，干扰抓取作业的无人机扰动被隔离.其中，风力扰动利用simAddForceAndTorque() 函数施加在无人机本体上，在世界坐标系y轴正方向施加正弦信号力，在世界坐标系x轴正方向施加随机信号力.

图8 抓取增稳算法框图

3.3 仿真结果

无人机抓取增稳算法的可视化仿真结果如图9所示.无人机受气流扰动时，机械臂末端抓手可以牢牢抓住杯子，并可保证杯子中的小球不掉落.

建立V-REP与MATLAB软件的Sockets通信后，绘制三维散点图，如图10(a)所示.其中，点的颜色代表杯子实际位置与杯子理想位置的距离d.经过抓取增稳算法补偿后，机械臂抓手的最大位置偏差值为0.1 m，相比于无人机位置最大偏差值0.4 m有显著减小，如图10(b)所示.其中，E为距离偏差；EUAV为无人机距离偏差值；Em为机械抓手距离偏差值.由图10可见，抓取增稳算法的效果显著.

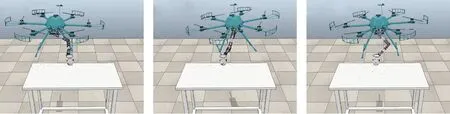
图9 抓取增稳算法的可视化仿真结果

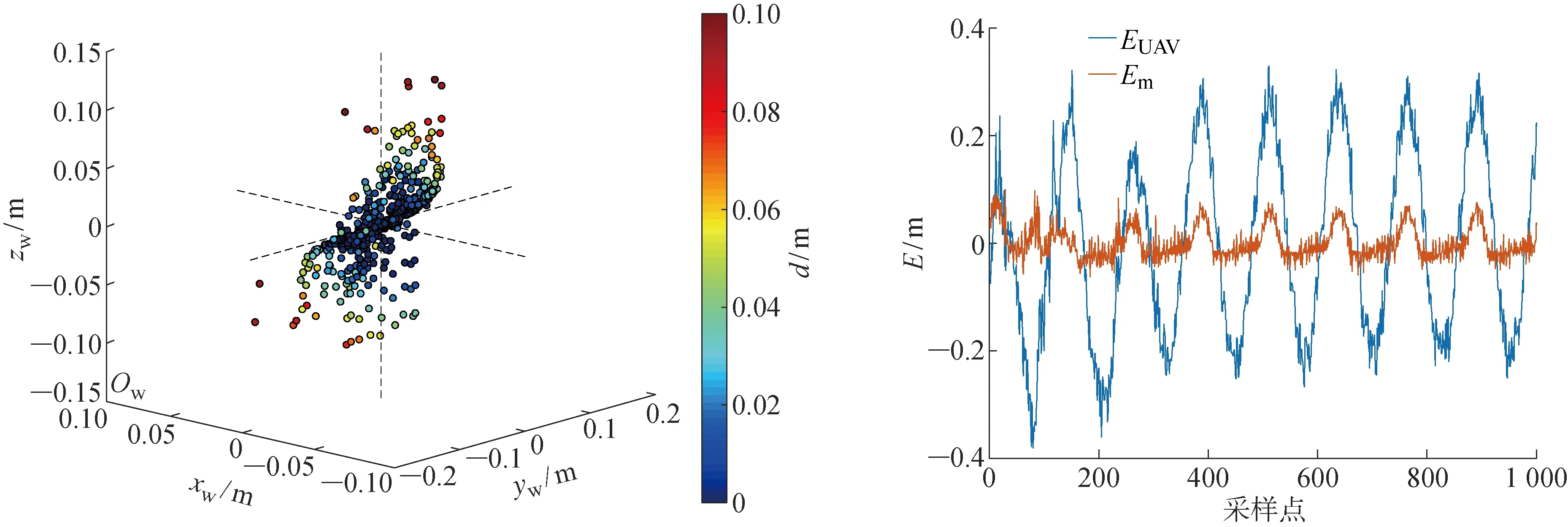
图10 抓手实际位置与理想位置对比图

4 结论

(1) 基于V-REP软件的二次开发，研制了一套多功能仿真实验平台，实现了无人机-机械臂动力学可视化仿真操作，在仿真层面提出了一套完整的空中抓取解决方案.

(2) 基于整机仿真平台，开发验证了2种算法，即基于质心实时采集的无人机增稳算法，其创新点是将机械臂对无人机的扰动简化为机械臂质心对无人机的扰动，针对准静态作业模式从无人机层面进行增稳；基于逆运动学的抓取增稳算法，其创新点是将运动学逆解算法应用于无人机增稳抓取操作中，从机械臂层面进行增稳.通过逐级增稳的方式，实现了无人机空中抓取作业的精细化操作.

致谢本文为上海交通大学机械与动力工程学院第四届研究生项目式实践课程获奖成果.感谢小组成员马昭、吕石磊、任书峰、李晓凯为本文研究提供的机械臂模型.