基于非侵入式混沌多项式法的随机阻曳流CFD模拟不确定度量化

夏 立， 邹早建,b， 袁 帅， 曾智华

(上海交通大学 a. 船舶海洋与建筑工程学院； b. 海洋工程国家重点实验室， 上海 200240)

随着计算机科学技术的飞速发展，计算流体动力学(Computational Fluid Dynamics，CFD)技术在工业生产和科学研究中得到了广泛的应用.而CFD的计算质量和可信度一直备受关注.目前船舶CFD不确定度分析研究主要集中在验证与确认(Verification and Validation, V&V).验证(Verification)是对数值误差进行分析，以保证数值方法的准确性；而确认(Validation)主要将数值计算结果和实验数据进行对比，以评估CFD数值模拟和真实物理模型的相似程度.在V&V分析中，CFD模型和数值方法是确定的，流动参数、几何模型和边界条件等因素都是确定量，获得的结果也是确定的量.然而在真实的物理环境中，许多物理量往往是不确定的，比如流动参数、几何模型和边界条件.这些不确定量的累积，可能会对系统的响应造成很大的影响.

实际上，CFD不确定度量化主要包含两方面的内容：其一是确定随机变量的分布情况；其二是量化由随机变量引起的不确定性对模型输出参数的影响.本文重点关注第二方面，即假定随机变量的分布情况是已知的，研究不确定性如何在流场中传播.

不确定度量化的传统方法可分为两种：一是非统计方法，如局部敏感度分析、矩量法和摄动法，可以解决不确定性较小的问题或线性系统问题；二是统计方法，如蒙特卡洛(Monte Carlo，MC)法等.MC法虽可求解非线性系统的不确定度量化问题，但其本质上是基于多次重复独立的数值模拟.使用MC法进行不确定度量化研究，需要对n维空间中的随机参数进行采样，这些采样点即为计算的工况，最后根据计算结果进行统计分析，得到响应量的统计特性.若要使响应量的期望概率水平达到10-n，至少需要生成10n+2个样本点[1].故该方法计算效率低、成本高，在工程实际问题中，往往被当作最后的求解手段.

近年来，混沌多项式(Polynomial Chaos，PC)方法被用于不确定度量化研究.该方法源于Wiener[2]提出的齐次混沌方法，而后由Ghanem等[3]发展到固体力学领域.近年来，该方法也被应用到CFD领域[4-18].在船舶计算水动力学方面，不确定度量化研究相对很少.He等[19]使用非侵入式混沌多项式方法，将船体形状、航速、波浪分别作为随机的输入变量，就Delft Catamaran船的水动力性能进行了不确定度量化分析.Diez等[20]使用代理模型、正交法和Karhunen-Loève展开法就Delft Catamaran船的阻力和下蹲进行了不确定度量化分析.Stern等[21]就船舶水动力学的不确定度量化问题及其验证方法进行了综述.

本文比较了验证与确认方法和不确定度量化的区别，分析了不确定度量化的研究现状；介绍了不确定度量化问题的定义以及用于解决该问题的非侵入式混沌多项式方法，并以随机二维阻曳流为例分析和讨论了计算结果.

1 数学模型

根据是否需要对求解器进行修改，PC方法分为侵入式混沌多项式(Intrusive Polynomial Chaos, IPC)法和非侵入式混沌多项式(Non-Intrusive Polynomial Chaos, NIPC)法.其中IPC法需要对求解器进行大量修改，其具体步骤为将控制方程的解展开成混沌多项式的形式，并将其代入控制方程、边界条件、初始条件等，通过改写后的方程求取混沌多项式的待定系数.IPC法改写求解器的工作量巨大，目前只应用于简单的随机CFD不确定度量化问题.NIPC法不需要改变CFD求解器，只需将其当作一个黑箱，随机输入变量和响应量之间的关系是通过满足一定条件的正交基函数的线性组合来表示的，即通过混沌多项式展开式来表示.因此，当混沌多项式的待定系数确定后，就可以获得响应量的全部概率分布信息，大大提高了计算效率.近年来，NIPC法由于其高效性，逐渐被应用于不确定度量化研究.本文采用NIPC法，以随机二维阻曳流为例进行不确定度量化分析.

1.1 问题定义

不确定度量化问题可以定义为已知随机变量ξ(输入变量)的分布，确定响应Y(输出变量)的分布情况，如下式：

Y=f(x,t,ξ)

(1)

式中：x为空间变量；t为时间变量；ξ为满足一定分布的随机变量组成的向量.

根据混沌多项式的理论，若函数空间是以内积定义为L2范数的Hilbert空间，且空间中的输入变量ξ是独立的，则响应Y可以分成确定的和随机的两部分：

(2)

式中：ci为待定的系数，只和确定的空间变量及时间变量有关；d为随机变量的个数；Φi(i=1,2,…)为混沌多项式，只和随机变量ξ有关.

为了求解实际问题，通常需要将式(2)进行截断.若将混沌多项式展开到p阶，则截断后的多项式形式如下：

(3)

式中：混沌多项式的系数共有Nc个，

(4)

1.2 混沌多项式

若随机变量服从高斯分布，则最优的多项式是Hermite多项式.Xiu和Karniadakis发展了基于Wiener-Askey方法的混沌多项式求解方法[4]，应用该方法可以求出多种服从典型分布的随机变量对应的混沌多项式，如表1所示.

表1 不同分布对应的混沌多项式

1.3 非侵入式混沌多项式方法

NIPC法可分为基于正交的方法和基于回归的方法两种.基于正交的方法主要是利用混沌多项式的正交性，求取混沌多项式的系数.但这种方法需要积分，而数值积分方法通常采用高斯积分法，所以采样点一般选为高斯点.然而，该方法会随着不确定量的维数增加而产生大量的采样点，大大增加工作量，即发生所谓的维数灾难.

本文采用的是基于回归的NIPC法.该方法首先需要生成满足分布的特定采样点，然后在这些点上进行CFD计算，得到响应Y后，通过混沌多项式的系数求出所关心的量的分布情况.

超定方程可以表示成下式：

(5)

写成矩阵与向量的形式为

Φc=y

(6)

待定系数可以通过最小二乘法求得：

c=(ΦTΦ)-1ΦTy

(7)

与基于正交的方法不同，该方法需要很好地配置采样点，而不是选取高斯积分时的高斯点.采样点的个数通常取2倍的混沌多项式的待定系数的个数[14]，即2Nc.

在求取混沌多项式的待定系数后，响应Y的均值与方差可以通过以下两式得到：

2 采样方法

本文采用随机采样(Random Sampling，RS)法和拉丁超立方采样(Latin Hypercube Sampling，LHS)法进行采样.这两种算法均能生成符合特定分布的随机数.LHS法本质上是一种受约束的分层随机采样方法，针对有众多随机变量的问题特别有效.LHS法在满足随机变量的分布情况的同时，可以大大减少采样点.从有着d维不确定量的系统中抽取N个样本的具体步骤如下：

(1) 将每一维度分成等概率的N个区间(例如，均匀分布时区间的长度相同)；

(2) 在上述各个区间中随机抽取一个点，且满足每个与轴垂直的超平面最多含有一个样本.

可以看出，样本总数N并不会随着随机变量的维数而增加.对于高维问题，LHS法可以大大减少采样点，从而减小计算量.

3 二维随机阻曳流算例

3.1 求解实例

如图1所示，以下平板的某一点为原点建立坐标系，其中x方向与上平板的拖曳方向一致，y方向垂直于x轴向上. 两平行平板间为牛顿流体，其黏度为μ=1 kPa·s.上下壁面均满足壁面无滑移假设，即流体速度与壁面速度一致.上平板拖曳速度为u=0.01 m/s，v=0；下平板为固面，u=0，v=0.本文将左右两边的入口压力p1和出口压力p2处理为不确定量，且满足均匀分布U(950 Pa, 1 050 Pa).采用速度-压力有限元方法[22]对算例进行求解.

图1 二维阻曳流模型

3.2 控制方程

该问题实际为求解在进出口压力和拖曳复合作用下定常的二维流场分布.其连续性方程可以表示为

(10)

x方向运动方程：

(11)

y方向运动方程：

(12)

(13)

式中：τ为切应力，满足牛顿流体本构方程.

3.3 网格收敛性分析

本文使用四边形单元对计算域进行离散；速度单元阶次比压力单元高一次，以便提高计算精度.为确定合适的网格数量，首先进行网格收敛性分析，采用GCI(Grid Convergence Index)方法[23]进行网格收敛性验证.网格收敛性分析必须在确定条件下进行.本文网格收敛性分析采用的工况为入口压力p1=1 kPa，出口压力p2=0.共采用了粗、中、细3套网格，网格数分别为9×9、14×14以及19×19.根据GCI方法，获得细网格、中等密度网格和粗网格对应的数值计算结果φ1、φ2、φ3，据此可得到近似相对误差、外推相对误差和细网格收敛指数.需要指出的是，当ε21=φ2-φ1和ε32=φ3-φ2都接近于0时，可以认为已经得到了精确解.本文以出口边界中点处的速度值作为网格收敛性分析的标准，求得的φ1、φ2、φ3分别为 10.624 9、10.625 0和 10.625 0 mm/s.可以认为这3套网格都得到了精确解.最终采用的网格离散情况如图2所示.

图2 计算域网格离散

4 计算结果与讨论

4.1 计算结果

本文分别采用MC法和基于回归的NIPC法对二维随机阻曳流进行了不确定度量化分析.其中MC法选用了基于RS的MC法(MC-RS)和基于LHS的MC法(MC-LHS).本算例所关心的输出量为下平板的压力分布，即对下平板各点处的压力p进行不确定度量化，得到其均值与方差.

应用MC法进行不确定度量化的主要步骤如下：

(1) 确定随机变量的分布；

(2) 用蒙特卡洛法生成采样点；

(3) 在这些采样点上进行CFD计算；

(4) 统计这些计算结果，得到所关心的量的均值、方差等统计特性.

应用基于回归的NIPC法进行不确定度量化的主要步骤，其前3步与应用MC法的相同，其后步骤如下：

(4) 根据随机变量分布，确定混沌多项式的形式；

(5) 根据计算结果，拟合出混沌多项式的待定系数；

(6) 根据所求系数，得出所关心的量的均值、方差等统计特性.

计算结果如图3～6所示.其中各幅图的图(a)展示了各个采样点上的CFD计算结果；图(b)展示了MC法的结果，即对图(a)所展示的计算结果进行统计分析得到的统计特性；图(c)展示了两种方法(MC和NIPC)求得的统计特性的相对误差η；图(d)展示了NIPC法的结果，即对图(a)所展示的计算结果按NIPC法进行后处理，在求取混沌多项式系数后，按式(8)和(9)得到统计特性.

图3 MC-RS方法12次模拟结果

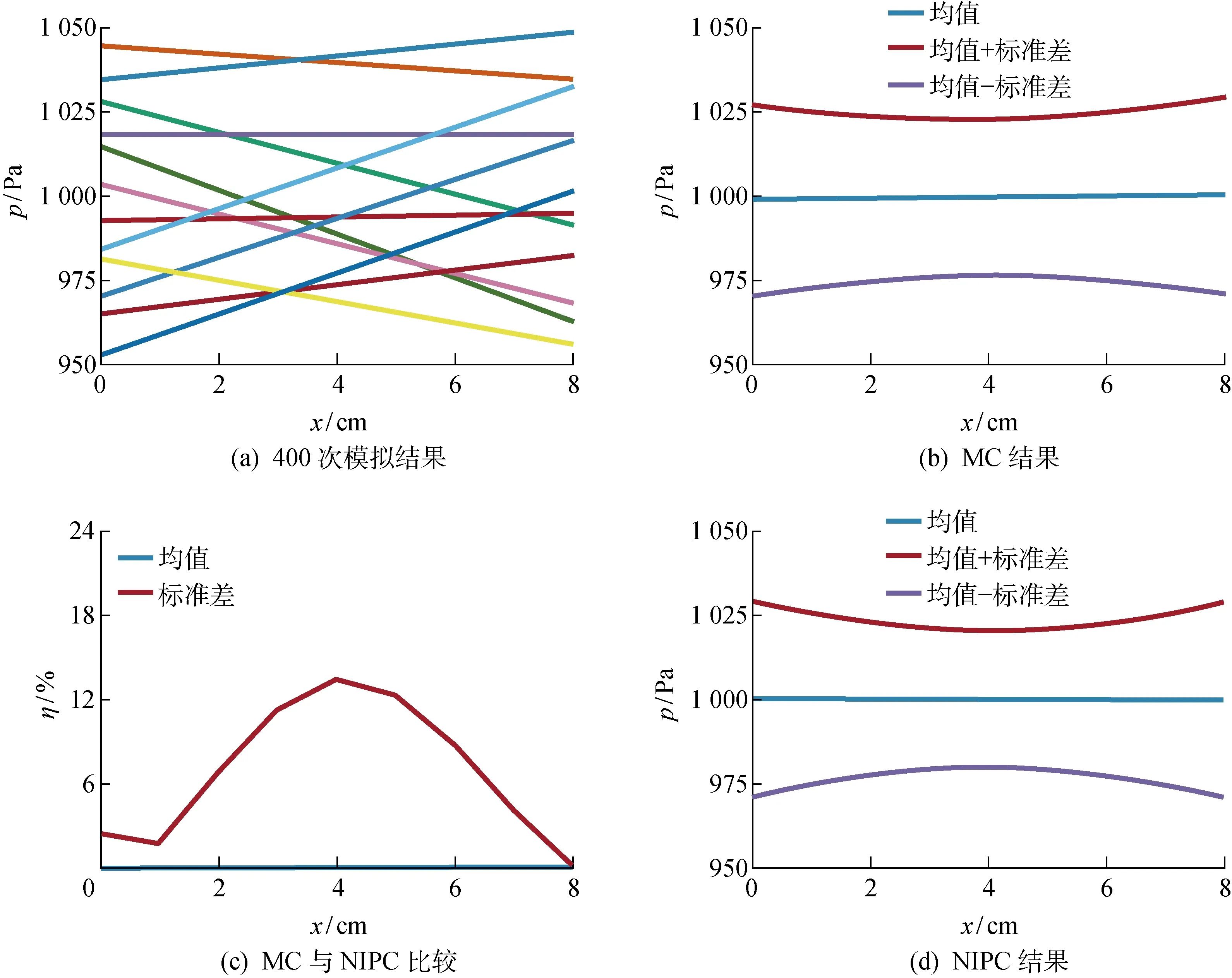
图4 MC-LHS方法12次模拟结果

图5 MC-LHS方法48次模拟结果

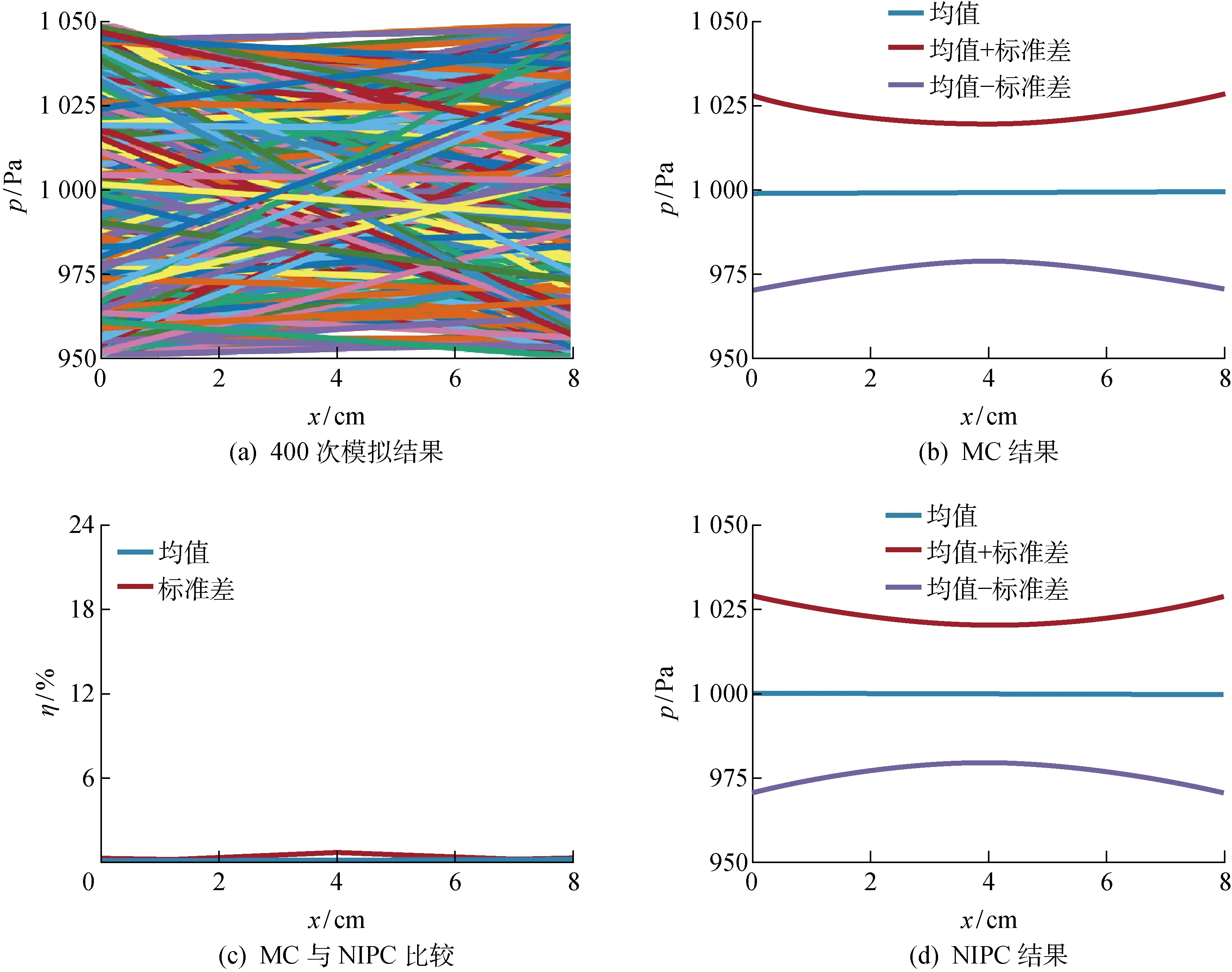
图6 MC-RS方法400次模拟结果

4.2 结果分析

首先分析采用基于两种采样方法的MC法进行不确定度量化研究的结果.对比图3(c)和图4(c)可以发现，MC-RS和MC-LHS两者得到的均值结果较好，但方差有较大误差.从图5(c)和图6(c)可以看出，随着模拟次数的增加，方差的误差也随之减小.

再比较采用MC法与NIPC法分别进行不确定度量化研究的结果.从图3～6的图(b)可以看出，使用MC法进行不确定度量化，输出量的统计特性随着模拟次数的增加而缓慢收敛；而从图(d)可以看出，使用NIPC法进行不确定度量化，其结果收敛较快且并不依赖采样方法.从图3(d)、图4(d)、图5(d)与图6(c)的比较可以发现，经过12、48次模拟，并用NIPC法处理后所得到的下平板压力的统计特性，与用MC法模拟400次后统计出的均值、方差相差无几，说明NIPC法可以更好地对该随机CFD问题进行不确定度量化，即在生成的采样点较少时，NIPC法也能很好地进行不确定度量化.

5 结语

本文分别采用MC法和基于回归的NIPC法研究了由于边界条件引起的不确定性在平板间阻曳流流场中的传播，验证了NIPC法求解不确定度量化问题的有效性.结果表明：应用基于不同采样方法的MC法进行不确定度量化的结果相差不大，但效果都远不如NIPC法.

下一步将开展混沌多项式展开的阶数对不确定性传播的影响的研究，以及基于正交的NIPC法与基于回归的NIPC法的比较.就实际的船舶水动力学问题而言，随机因素也大量存在，如海洋环境中的随机海流、随机海浪，船体制造工艺引起的误差，船体质量分布偏差等，今后可将NIPC法应用于随机的基于CFD的船舶水动力性能预报问题.