基于一种混合智能算法的有限元模型修正多解问题

康俊涛， 张亚州， 秦世强

(武汉理工大学 土木工程与建筑学院， 武汉 430070)

桥梁结构健康监测需要对结构响应进行实时监测分析，并通过对比基准有限元模型计算响应与结构的实际响应来分析构件损伤位置及损伤程度，及时进行预警[1].然而，由于建模时的简化、结构尺寸的变异、材料性能的不确定性等，按照设计图纸建造的初始有限元模型与结构实际情况存在一定的差异，并不能作为结构健康监测的基准模型[2].利用结构实测信息可以提高有限元模型对实际结构的模拟精度.通过改变初始有限元模型中的结构设计参数(如材料弹性模量、支座约束等)以达到有限元模型计算响应与结构的实际响应相符合的目的，该技术称为有限元模型修正技术[3].

有限元模型修正[4]通过以下分析过程来实现：首先对实际结构进行静动力测试，并根据测试信号分析出结构的静动力特性(如结构频率、模态振型等)；其次对按照图纸建造的初始有限元模型进行分析，得出模型静动力特性；然后利用结构实测特性与模型计算特性之间的误差构建目标函数；最后通过最优化方法寻找目标函数的最小值来完成有限元模型修正.

有限模型修正研究较广，传统的有限元模型修正仅提供一个使得目标函数取得最小值的修正结果[5].然而一些学者指出，由于结构的复杂性、测试信息的不完备、测试噪声等原因，用于构建目标函数的结构特性并不一定能完全代表结构的实际特性，从而导致目标函数的最小值所对应的修正结果并不一定能代表结构的实际情况，一些局部最优解可能更好地代表结构实际情况[6-7].因此，由传统的仅提供一个有限元模型修正结果转变为提供多个修正结果，然后让决策者根据经验和现场实际情况来确定最终采用的修正结果显得更为合理[8].

为提供多个修正结果，学者们主要采取了以下几种方法：全局优化算法[9-10](Global Optimization Algorithms，GOAs)，小生境技术[11](Sequential Niche Technique，SNT)和多模型建模[6](Modeling to Generate Alternatives，MGA).GOAs通过对整个可行域进行系统地搜索来获取全局最优和一些局部最优值.GOAs在模型修正领域应用较广，但大部分研究集中在寻找全局最优，而丢弃局部最优，且对局部最优的质量不予评价.SNT需要和其他优化算法配合使用.每次寻优需要运行一次优化算法，并记录寻找到的最优解及其所处区域，在下一次寻优时排除此前记录的寻找到极值的区域，在剩余区域内再次进行寻优.SNT算法对参数空间的搜索更加详尽和科学，每次在更小的参数空间进行寻优提高了优化算法的寻优精度，但与SNT配合使用的优化算法多为进化算法，每寻找一个局部最优值都需要多次迭代，因此完成整个寻优过程需要花费大量时间.MGA方法旨在提供多个修正结果，这些结果具有相近的目标函数值，但是自变量的值却相差较大.在模型修正领域，多位学者[6-7]采用MGA方法提供了多个修正结果.MGA通过参数及选择策略的设置可以极大地提高优化速度，但同时解的精度会有所损失.

综上所述，为提供多个模型优化结果，本文将寻优速度快的稳态遗传算法(Steady-State Genetic Algorithm，SSGA)和寻优精度高的梯度下降(Gradient Descent，GD)算法相结合，提出了一种混合智能算法，该算法在保证优化速度的同时，提高了优化精度.最后分别采用数值函数和ASCE-Benchmark数值结构模型对所提混合智能算法性能进行了验证.

1 有限元模型修正及多解问题

有限元模型修正属于逆问题，即根据响应输出来推测系统属性.用数学语言可以将其描述为

X=f-1(Y)

(1)

式中：X为结构的系统输入；Y为结构响应；f为结构的系统属性.有限元模型修正的过程可以描述为：通过改变结构的系统属性f(如材料弹性模量、支座刚度等)来减小结构实际响应与有限元(FE)模型计算响应之间的误差，即

changef→min|YRE-YFE|

(2)

式中：YRE为结构实际响应；YFE为有限元计算响应.

如图1所示，同一个结构的实际响应是一定的，但是由于结构测试时传感器摆放位置不同，测试信号的处理方式不同，构建目标函数时采取的模态阶次不同等，用于模型修正的响应Y可能会有区别，从而导致修正结果即系统属性f的不同.

图1 模型修正中多解问题的产生示意图

如图2所示，采用5阶模态频率及振型所构建的目标函数在A处有更低的目标函数值，但是B处的目标函数值与A处目标函数值非常接近.然而如果在目标函数中增加第6阶模态信息，那么目标函数值会发生变化，B处所对应的目标函数值可能会比A处更低.

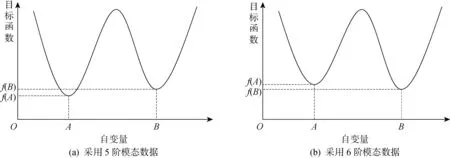
图2 目标函数

有学者[12-13]指出，由于目标函数中不可能包含所有的结构信息，所以有可能造成真实结构损伤所对应的目标函数值比全局最优目标函数值大的现象.而传统的有限元模型修正只提供一个最优修正结果，这可能会漏掉能够代表结构真实情况的修正结果.因此，在寻找全局最优解的同时，也寻找到在目标函数值上与全局最优解目标函数值相接近，但是在自变量上相距较远的局部最优解，这样显得更为合理.

2 基本算法介绍

2.1 稳态遗传算法

稳态遗传算法最先由Syswerda[14]提出，Caicedo等[6]对其进行了改进，提出了高效率的稳态遗传算法，所提算法以遗传算法为基础，同时增加了MGA解及其伴侣解的选择过程，并且后续的交叉、变异也仅在MGA解及其伴侣解之间进行.文献[6]将MGA解定义为在目标函数值上相近，但在自变量上具有一定距离的解.最终的模型修正结果即是MGA解集内的元素.MGA解的伴侣解被定义为在目标函数值上与MGA解相近，且在自变量上与MGA解相接近的一个解.在判定两个解的距离远近时，作者采用了两个解与某一定点所形成的夹角的大小.

在每轮迭代更新中，只有部分子代取代父代，因此只需计算新个体的目标函数值即可.对于复杂模型的修正，在优化过程中最为耗时的就是计算个体的目标函数值，因此，稳态遗传算法的最大特点就是优化速度快.

由于稳态遗传算法设置为每轮迭代由部分更优的子代取代较差的父代，所以在迭代后期会出现目标函数值更优的子代取代较差父代MGA解的情况，最终导致MGA解只剩下最优的一个值.为了保证MGA解的个数，稳态遗传算法选择在MGA解有多个的时候终止迭代，导致最终解的精度不高.

2.2 梯度下降算法

梯度下降算法利用个体所处位置的梯度，也即最速下降方向进行优化.由于只利用个体所处位置信息进行寻优，因此梯度下降算法具有很快的寻优速度，且具有易于实现的特点.

梯度下降算法中采用下式进行迭代更新解的位置：

(3)

由于梯度下降算法中个体只感知周围很小一个区域的梯度信息，所以梯度下降算法很容易陷于局部最优，且个体的最终优化结果与其初始位置密切相关，即使初始位置相近的两个个体，最终也可能优化出两个完全不同的结果.

3 基于SSGA和GD的混合智能算法

3.1 算法思想

混合智能算法(SSGA-GD)将SSGA和GD算法相结合，分别利用各自算法的优点.在算法前期利用SSGA搜索速度快和搜索域广的优点，当个体不再进化或者进化速度慢时，让个体进入GD算法，利用GD算法局部搜索速度快和搜索精度高的特点来提高MGA解的精度.在GD算法中，个体的初始位置也即是MGA解的位置，因此解决了GD算法对初始位置敏感的问题.

3.2 算法流程

本文所提算法流程如图3所示，具体步骤如下.

步骤1在自变量的定义域内初始化种群.SSGA每次迭代只计算很少一部分个体的目标函数值，因此种群中个体数量的增加并不会显著增加计算量，但是较多的个体数量会增加寻找到最优值的概率.

步骤2计算每个个体的目标函数值，并据此将所有个体进行排序.

步骤3排序后的种群中，第一个个体自动选为MGA解，剩余个体按照顺序计算是否满足以下两个条件，满足则选为MGA解，否则忽略.

条件1该个体与MGA解集中所有元素形成的夹角θ大于设定值，如图4所示.

图3 混合智能算法计算流程

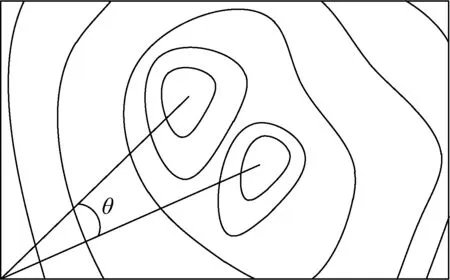
图4 角度控制示意图

即需要满足：

(4)

式中：θ1和θ2分别为该个体与已有MGA解形成的夹角；α为设定的夹角控制值.

条件2该个体与最优MGA解的目标函数值之比小于设定值：

(5)

式中：J1为最优MGA解对应的目标函数值；Ji为该个体的目标函数值；β为设定的目标函数控制值.

步骤4判断是否进入GD程序，如果进入则将所有的MGA解分别作为一个初始位置进行梯度寻优.否则进入下一步骤.本文设置个体是否进入GD的判定准则为：在最近的5次迭代过程中MGA解的优化程度小于一个定值(本文取定值为10-5)，此值可根据问题特点进行修改，取值越小，进入GD的概率越小，反之则越大.

步骤5寻找每个MGA解的伴侣解，伴侣解需要满足以下两个条件：

条件1MGA解与其伴侣解之间的夹角θc小于设定值α，即

θc<α

(6)

条件2MGA解与其伴侣解目标函数值之间比值大于设定值，即

(7)

式中：Ji为该MGA解对应的目标函数值；Ji c为该MGA解对应伴侣解的目标函数值；β为设定的目标函数控制值.

步骤6MGA解与其伴侣解之间进行交叉，产生的新个体进行变异，并计算新个体的目标函数值.

步骤7根据新个体的目标函数值，采用轮盘赌策略以一定的概率用新产生的子代个体替换父代个体.

步骤8判断是否满足迭代终止条件，满足则结束，输出MGA解集，否则进入步骤3.本文设置迭代终止条件为迭代次数达到上限.

3.3 数值算例

采用 Rastrigin’s Path函数测试算法寻找多个极值的能力以及在寻优精度上的表现，函数如下：

(8)

式中：n为问题的维度；Xi为问题的自变量.

Rastrigin’s Path函数图像如图5所示.参数每个维度的定义域均为[-1,1]，在定义域内，函数共有4个峰值，分别位于(0.502 6,0.502 6), (-0.502 6, -0.502 6), (-0.502 6,0.502 6), (0.502 6,-0.502 6) 附近，且4个峰值的目标函数值相同.

图5 Rastrigin’s Path函数图像

采用SSGA-GD进行多解寻优，同时将SSGA作为对比算法验证算法性能.两种算法的基本参数设定相同，不同之处在于SSGA-GD在进化过程中MGA解增加了梯度寻优的过程.参数设置如表1所示.表中α和β的取值可根据问题的特点进行改变，cosα取值越大，最终修正结果的数量越多；β取值越小，最终修正结果的数量越多，但排序靠后的MGA解的质量也越差.

由于4个极值对称分布，且目标函数值相同，将每轮迭代过程中算法寻找到的4个MGA解的目标函数值的平均值作图，结果如图6所示.可以看出，相较于稳态遗传算法，改进的算法具有更快的优化速度，并且在精度上也有明显的提升.表2为最后的优化结果，可以看出，在计算时间仅增加0.13%的情况下，改进算法寻找到的4个极值均具有更高的精度.

表1 SSGA-GD参数设置

图6 SSGA和SSGA-GD迭代曲线

表2 SSGA与SSGA-GD结果对比

4 有限元模型修正

4.1 ASCE-Benchmark模型

为了给不同的模型修正方法提供一个统一的对比和评价平台，国际结构控制协会(IASC)和美国土木工程协会(ASCE)于1998年在位于加拿大的英属哥伦比亚大学(UBC)建立了ASCE-Benchmark模型[15]，如图7所示.

图7 ASCE-Benchmark结构

ASCE-Benchmark模型为一钢框架模型，建立于加拿大UBC地震工程实验室.该结构为4层等高、2×2等跨的钢结构框架，层高3.6 m，每跨2.5 m.为了能够模拟实际情况，在第1、2、3层设置楼板，第1层楼板的质量为4×800 kg，第2、3层板的质量为4×600 kg，第4层楼板有对称和非对称两种设置方式，质量分别为4×400 kg和(3×400+1×550) kg.在每层中设置斜撑.结构钢材屈服强度为300 MPa.支撑、梁以及柱的截面尺寸及材料属性如表3所示.

表3 ASCE-Benchmark参数

4.2 有限元模型及模态试验

根据ASCE-Benchmark模型[16]建立的有限元模型共含有36个节点和116个单元，每个节点有3个独立的自由度Dx，Dy，Rz，每层楼板有共同的Dx，Dy，Rz3个自由度，共120个自由度.其中，梁和柱采用欧拉-伯努利梁单元进行模拟，斜撑采用拉压杆单元进行模拟.

图8 ASCE-Benchmark结构的有限元模型及损伤位置示意图

图9 模态识别稳态图

本文设置的损伤形式如图8所示.选取120个自由度非对称结构有限元模型，为便于得到可视化结果，共选取两组参数进行修正，杆件53、54的弹性模量为变量X1，杆件33、57、58的弹性模量为变量X2，设置损伤工况为X1弹性模量损伤为初始弹性模量的30%，X2为初始弹性模量的90%.

利用有限元程序计算结构在设定损伤工况下的瞬态响应，记录每层的x、y两个方向的加速度响应.对得到的响应数据利用随机子空间法(Stochastic Subspace Identification, SSI)[17]进行模态识别，并利用稳态图(见图9)辅助确定模态阶次，识别结果如表4所示(ft为频率识别值).频率、阻尼比和振型的稳定准则分别为相邻两阶的误差不超过两者中最小值的1%、5%和1%.

表4 SSI频率识别结果

4.3 ASCE-Benchmark有限元模型修正

根据识别结果和模型计算之间的误差构建目标函数.选取前5阶模态的自然频率和前4阶的模态振型和作为修正目标，构建目标函数

(9)

式中：fai为有限元模型分析得到的第i阶频率；fti为损伤模型随机子空间法识别出的频率结果；MACj为第j阶模态置信准则，

(10)

式中：φi和φj分别表示需要对比的两个阵型.MAC结果范围为[0 1]，越接近1，则说明两者越有可能是同一阶模态.

目标函数的图像如图10所示.从图像中可以看出，目标函数在(0.3,0.9)和(0.9,0.3)附近均有一个极值.

图10 目标函数图像

图11 SSGA和SSGA-GD迭代曲线

4.4 寻优结果及分析

分别采用SSGA和SSGA-GD对目标函数进行优化，算法中参数设置情况同上算例.将每轮迭代中前两个个体的目标函数值取平均，然后作图11，从图中可以看出，SSGA-GD优化速度明显优于SSGA.优化结果如表5和6所示.表6中误差的计算公式如下：

(11)

式中：E为误差；f为初始有限元模型的频率(fini)或修正后模型的频率(fup)；fid为识别的频率.

可以看出两种算法计算时间相差不大，且均寻找到了定义域内的两个极值.从图11、表5及表6中均可看出，SSGA-GD的寻优精度明显优于SSGA.从表6中可以看出， 初始有限元模型与实测结果有较大误差，频率最大差值达到9.15%.经过两种算法修正后误差均有减小，且SSGA-GD的修正精度优于SSGA的修正精度.SSGA-GD中，修正结果1与识别结果之间的最大误差仅为0.09%，其中多阶修正结果与实测结果相同，修正结果2与实测结果最大误差也仅为0.28%， 可以看出两个修正结果均具有较高的精度.

表5 SSGA和SSGA-GD结果对比

表6 有限元模型修正前后频率对比

5 结论

本文分析了有限元模型中的多解问题，并且为了寻找到全局最优以及质量较好的局部最优，将寻优速度快但精度低的稳态遗传算法与寻优精度高但受初始位置影响大的梯度下降算法相结合，分别利用两种算法的优点，提出了一种寻优速度快、精度高的混合智能算法.采用数值算例和ASCE-Benchmark模型修正过程测试了所提算法寻找多个解的能力，同时将稳态遗传算法作为对比算法，测试改进前后算法多解寻优能力及计算效率.

(1) 数值算例寻优结果表明，所提混合智能算法能寻找到自变量定义域内的多个极值，且相比于稳态遗传算法，改进的算法具有更高的寻优精度.

(2) 在有限元模型过程中，所提算法修正能准确找到定义域内的两个极值，且相对稳态遗传算法均具有更高的精度，优化后的结构频率误差最大值从9.15%分别下降到0.09%和0.28%，表明两个寻优结果均具有较高的精度.多个质量较优的修正结果可以为决策者提供更多的选择.