Remaining useful life prediction of aircraft lithium-ion batteries based on F-distribution particle filter and kernel smoothing algorithm

Ki ZHANG, Peng ZHAO, Cnfei SUN,c, Youren WANG,*,Zewng CHEN

a College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China

b Aviation Industry Corporation Leihua Electronic Technology Research Institute, Wuxi 214000, China

c Testing and Verification Center, Aviation Key Laboratory of Science and Technology on Fault Diagnosis and Health Management, Shanghai 201601, China

KEYWORDS F-distribution;Kernel smoothing;Lithium-ion batteries;Markov model;Particle filter;Prediction;Remaining useful life

Abstract As an emergency and auxiliary power source for aircraft, lithium (Li)-ion batteries are important components of aerospace power systems. The Remaining Useful Life (RUL) prediction of Li-ion batteries is a key technology to ensure the reliable operation of aviation power systems.Particle Filter (PF) is an effective method to predict the RUL of Li-ion batteries because of its uncertainty representation and management ability. However, there are problems that particle weights cannot be updated in the prediction stage and particles degradation. To settle these issues,an innovative technique of F-distribution PF and Kernel Smoothing (FPFKS) algorithm is proposed.In the prediction stage,the weights of the particles are dynamically updated by the F kernel instead of being fixed all the time.Meanwhile,a first-order independent Markov capacity degradation model is established. Moreover, the kernel smoothing algorithm is integrated into PF, so that the variance of the parameters of capacity degradation model keeps invariant. Experiments based on NASA battery data sets show that FPFKS can be excellently applied to RUL prediction of Liion batteries.

1. Introduction

Lithium(Li)-ion batteries have the obvious advantages of high energy density, no memory effect, long cycle life, and so on.They have been widely used in the fields of airplane and spacecraft1. However, as the number of charge-discharge cycles increases, the available capacity of Li-ion batteries gradually declines. When the capacity drops below the threshold, the fault of Li-ion batteries can be identified2-3.This phenomenon seriously affects the life and safety of Li-ion batteries,and indirectly leads to performance degradation or malfunction of the aviation power system. However, the Remaining Useful Life(RUL) prediction uses known operational status information to predict how long it will take for the battery to reach the failure threshold from the current time.Therefore,accurate RUL prediction of Li-ion batteries can provide a decision-making reference for preventive maintenance of the aviation power system, and reduce the maintenance costs and the chance of fatal failures.

In recent years, the RUL prediction method of Li-ion batteries can be roughly divided into three types: data-driven methods,model-based methods and fusion-based technology4.For data-driven methods such as those of Zhang et al.5based on capacity data of the battery,the trend of the degradation of the battery capacity can be obtained through the Long Short-Term Memory Recurrent Neural Network (LSTM RNN)which is trained online recursively. The early RUL of the battery can also be realized through the offline data training network. Song et al.6used Kalman Filter (KF) and physical degradation models to optimize Relevance Vector Machine(RVM),and obtained good long-term prediction performance.The data-driven method is that the hidden health status information of the battery is directly extracted from battery performance test data and condition monitoring data (voltage,current, temperature, impedance, etc.) without considering the complex electrochemical reaction and failure mechanism inside the battery7-8. However, this method relies heavily on historical data and is susceptible to data uncertainty and incompleteness. Moreover, this method has high computational complexity and can only be applied offline. Besides,the battery is susceptible to internal chemical reactions and external environment variations, so its failure is random9-10.Data-driven regression prediction method can only obtain a single value of the RUL of the battery. When the predicted RUL of the battery exceeds the actual value too much, there will be a large hysteresis when replacing and maintaining the battery, and there will be a significant safety hazard in the power system during the following operation. Therefore,how to achieve uncertainty prediction is an urgent problem to be solved. Model-based prediction methods and prediction methods based on fusion techniques mostly use Particle Filter(PF) as a statistical random filtering algorithm to obtain the probability distribution of prediction results,that is,the uncertainty of prediction results. As for model-based methods, Lyu et al.11established a RUL prediction model for lead-acid batteries by combining degradation mechanism model and PF,and took degradation mechanism model parameters as state variables.The capacity simulation process based on the degradation mechanism model is used as the measurement equation,and PF is applied to updating the model parameters to predict the RUL of lead-acid batteries in real time. However, the degradation mechanism model has a high degree of complexity and many parameters,and the practical application is difficult.Guha and Patra12integrated the capacity degradation model and the internal resistance growth model to establish a fusion degradation model of Li-ion batteries. The model parameters are updated by the PF, and the battery RUL is obtained by model extrapolation. The prediction method based on fusion technology is a combination of model and data-driven method.For example, Liu et al.13studied a cycle life fusion prediction method of Li-ion batteries based on Nonlinear Degenerate AR(ND-AR) model and Regularized PF (RPF). The long-term degradation trend of capacity is estimated by the AR model,and the estimated capacity is taken as the measurement in the PF algorithm. The prediction result is adjusted to realize the cycle life prediction of Li-ion batteries more accurately,and the uncertainty expression of the prediction result is given by the Probability Density Function(PDF).Hu et al.14studied the RUL prediction of Li-ion batteries for medical devices based on a combination of model and data-driven method.Firstly, based on an RVM, the relationship between the characteristics of battery charging stage and battery capacity was established to obtain the battery capacity online. Then, the model parameters of battery degradation are updated by PF iteratively and the RUL of the battery is predicted.The above model-based methods and the prediction methods based on fusion technology can obtain the probability distribution of the prediction result by using the PF algorithm. However,the prediction methods based on fusion technology still have challenging problems such as high model complexity, a large amount of calculation, and uncertainty fusion. And PF itself has some shortcomings.The variance of the weight of the particles increases randomly with time so that the weight of the particles is concentrated on a few particles. The weights of other particles are small, negligible, and the problem of particle degradation occurs. The particle set cannot express the actual posterior PDF. Moreover, during the prediction process, the weight of the particles will remain constant, and the predicted capacity can only be recursively derived from the degenerate model, which will cause the particles’ information to deviate from the true posterior PDF of the state variable.Especially when there are less historical data and early RUL prediction, there will be a significant error in the RUL prediction. Guo et al.15proposed an F-distributed Particle Filter(FPF) and applied it to the RUL prediction of hydraulic system for the problem that the particle weight remains constant during the prediction process. But this method does not solve the problem of particle degradation. The precision of the prediction results is affected.

Therefore, in this paper, a first-order Markov model considering the uncertainty of Li-ion batteries degradation is established, and an F-distribution PF and Kernel Smoothing(FPFKS) algorithm is proposed and applied to the field of RUL prediction of Li-ion batteries. The FPFKS algorithm combines the advantages of the FPF algorithm and the Kernel Smoothing (KS) algorithm. The FPF algorithm changes the likelihood function of PF, and the weight of particles is calculated by F kernel dynamically. Moreover, the KS algorithm is integrated into the FPF so that the variance of the parameters of capacity degradation model remains fixed during the recursive propagation process, which ensures the integrity of the particle information and avoids the particle degradation problem. The FPFKS can achieve a joint estimation of prediction model parameters and states.Firstly,the parameters of capacity degradation model of Li-ion batteries can be updated recursively based on the KS algorithm. Then, the future capacities are recursively predicted based on the updated model, and each recursive prediction step updates the particle weights dynamically based on the F kernel structure to obtain upgraded capacities. Finally, the RUL of the battery is calculated when the preset capacity failure threshold is reached.The prediction model of this prediction method is relatively simple,and it is not necessary to use a large amount of historical data to train the model. The proposed prediction method has the advantages of small computational complexity and high prediction accuracy, and it is suitable for online prediction and has certain practical application value. Experimental results from two NASA capacity degradation data sets indicate that FPFKS can be effectively applied to RUL prediction of the battery.Compared to other typical methods,FPFKS has more accurate prediction results and a more precise uncertainty distribution of the PDF of RUL.

The rest of this paper is divided into the following sections.First, the FPFKS algorithm is described in detail in Section 2 and applied to the RUL prediction of Li-ion batteries. Then,Section 3 conducts experiments based on the battery data sets from NASA to evaluate the proposed method, and the novel method is compared with the other typical methods. Finally,the conclusions and future work are discussed in Section 4.

2. Prediction based on FPFKS

2.1. Aging model construction

PF needs to be combined with the system state model to track battery capacity degradation trend.Therefore,it is essential to establish a model that can accurately track the trend of battery capacity degradation. Due to the limitations of the above model of degradation mechanism of batteries, the double exponential model of capacity based on experimental data regression analysis is widely used. The model is as follows:

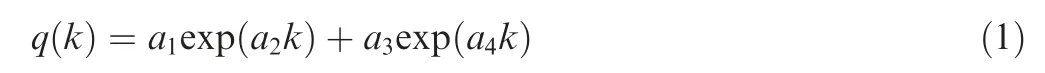
where k is the number of cycles of battery charge and discharge, q(k) is the capacity of the battery at the kth cycle,and a1,a2,a3,and a4are model parameters related to capacity degradation. Among these parameters, a1and a2are affected by the internal impedance of the battery, and a3and a4are affected by the aging rate of the battery.The double exponential model can well describe the capacity degradation trend.To apply this double exponential model to the FPFKS,this paper rewrites it into an iterative form that takes into account model uncertainty. The equation of state is

where θ1,θ2,θ3,and θ4are model parameters of the state equation, and N (0,) is Gaussian white noise with a variance of. The equation of state is a first-order independent Markov process. Taking into account the uncertainty of the measurement, the measurement equation used is

where Q(k)is the measurement at the kth cycle,and N(0,)is the measurement noise with a variance of.

2.2. FPFKS algorithm

PF is a nonlinear, non-Gaussian statistical filtering method based on Monte Carlo method and recursive Bayesian estimation15. PF can generate a set of random samples in the state space according to the empirical condition distribution of the system state variables, which are called particles. The weight and position of the particles are continuously adjusted according to the measurement, and the adjusted particle information corrects the initial empirical condition distribution.

In general,the equation of state and the measurement equation of a dynamic system can be expressed as

where xkis the state of the system at the kth time step,zkis the measurement of the system at the kth time step,f ·（）is the transition function of the state, and h ·（） is the measurement function. vkis the process noise at the kth time step, nkis the measurement noise at the kth time step,and they are generally assumed to be Gaussian white noise. θkis an unknown model parameter of the equation of state, where θk-1={θ1,k-1,θ2,k-1,θ3,k-1,θ4,k-1}, x(k)=q(k), z(k)=Q(k). In this paper, the KS algorithm based on beta distribution sampling is used to update the parameter particle sampling, which will be described in detail in Section 2.2.3.

Although PF is widely used in the field of RUL prediction,there are also problems that the weight cannot be updated in the prediction stage and the particles are degraded. The main reasons are as follows:

(1) Particles are weighted based on the error between the actual measurement and the estimated value and a Gaussian normal kernel given by

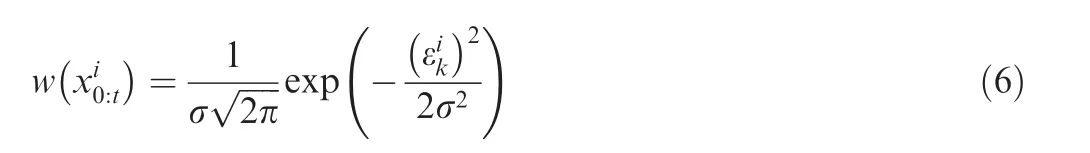
(2) PF selects the prior PDF as the important PDF. Since the current measurements are not taken into account,the sample values obtained from the important PDF are greatly different from those obtained from the true PDF. Therefore, the variance of the importance weights of particles increases randomly with time so that the weights of the particles are concentrated on a few particles. The weight of other particles is so small that it can be ignored, resulting in particle degradation,which ultimately makes the particle set unable to express true PDF.

(3) When using PF to estimate model parameters, random noise is usually added to establish dynamic parameter equations to increase particle diversity. However, increasing the random noise is likely to destroy the true PDF of the parameters. Eventually, the particle set no longer approximates the posterior PDF. The variance of the particle weight increases randomly with time, which also leads to particle degradation.

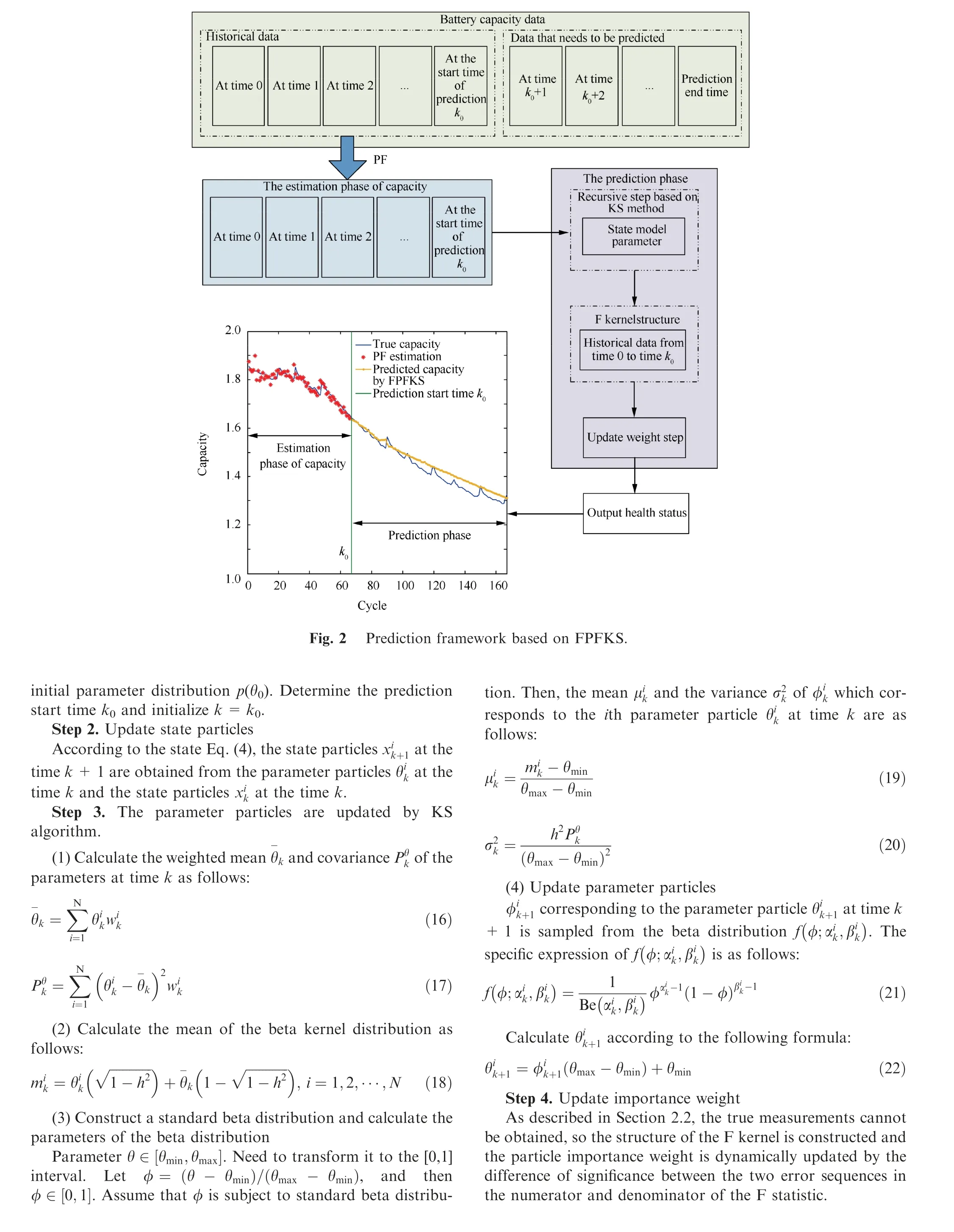
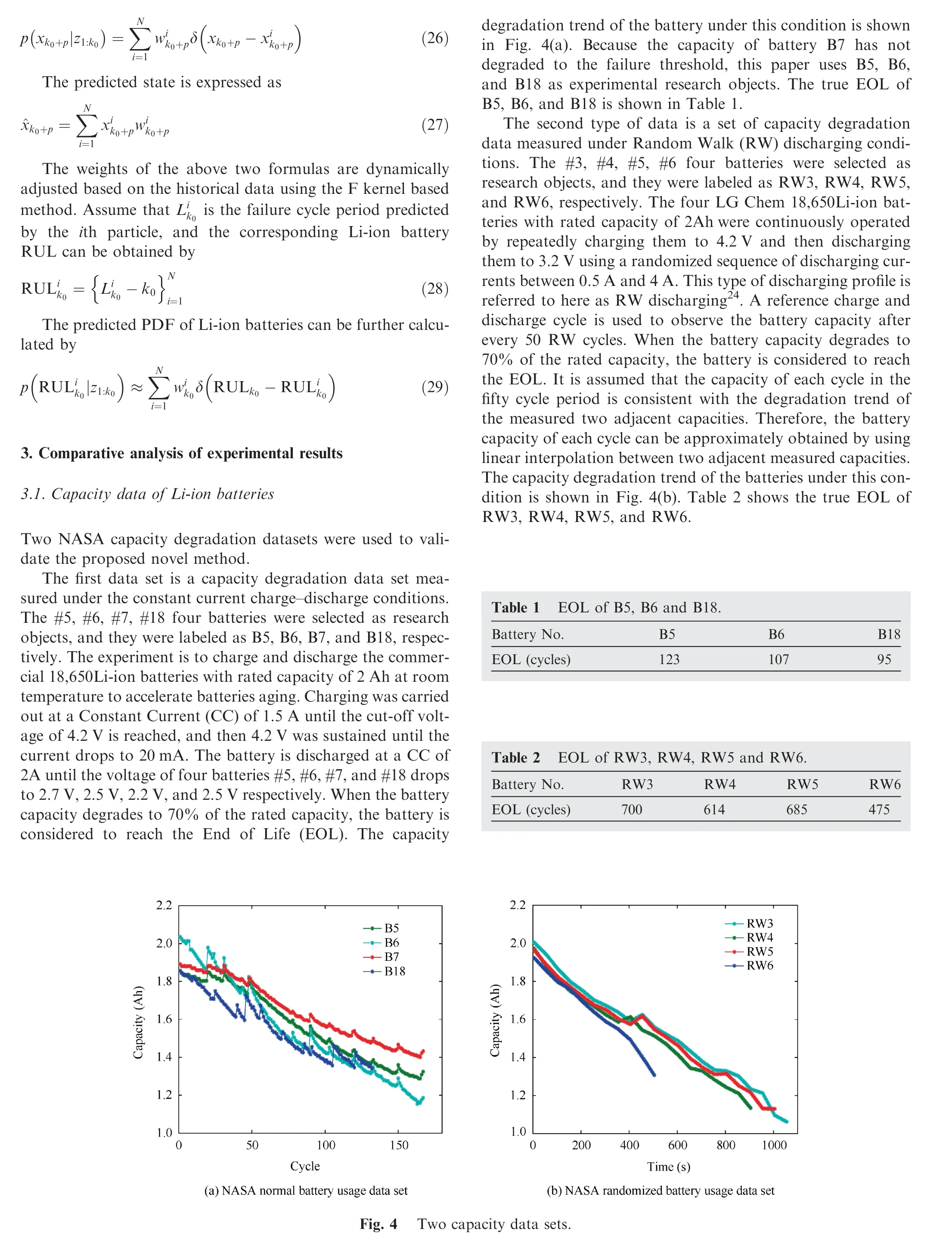
Fig. 5 RUL and RUL PDF results of B5 and RW4 predicted by FPFKS, PF and UPF.

3.2. Predicted performance indicator

To verify the predictive performance based on the FPFKS algorithm, three predictive performance indicators are used:Accuracy Index (AI), Precision Index (PI), and Root Mean Square Error (RMSE). These three predictive performance indicators are defined as

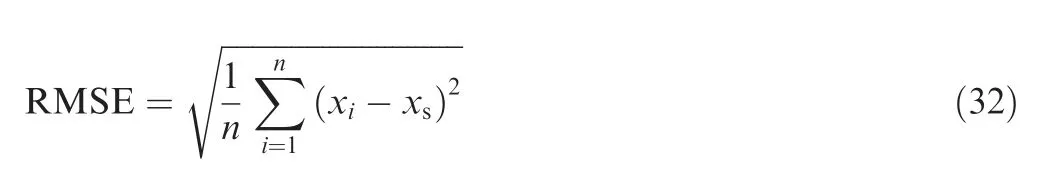
where RUL is the true RUL,and RUL is the predicted RUL.U CI is the utpper bound of the 90%conp

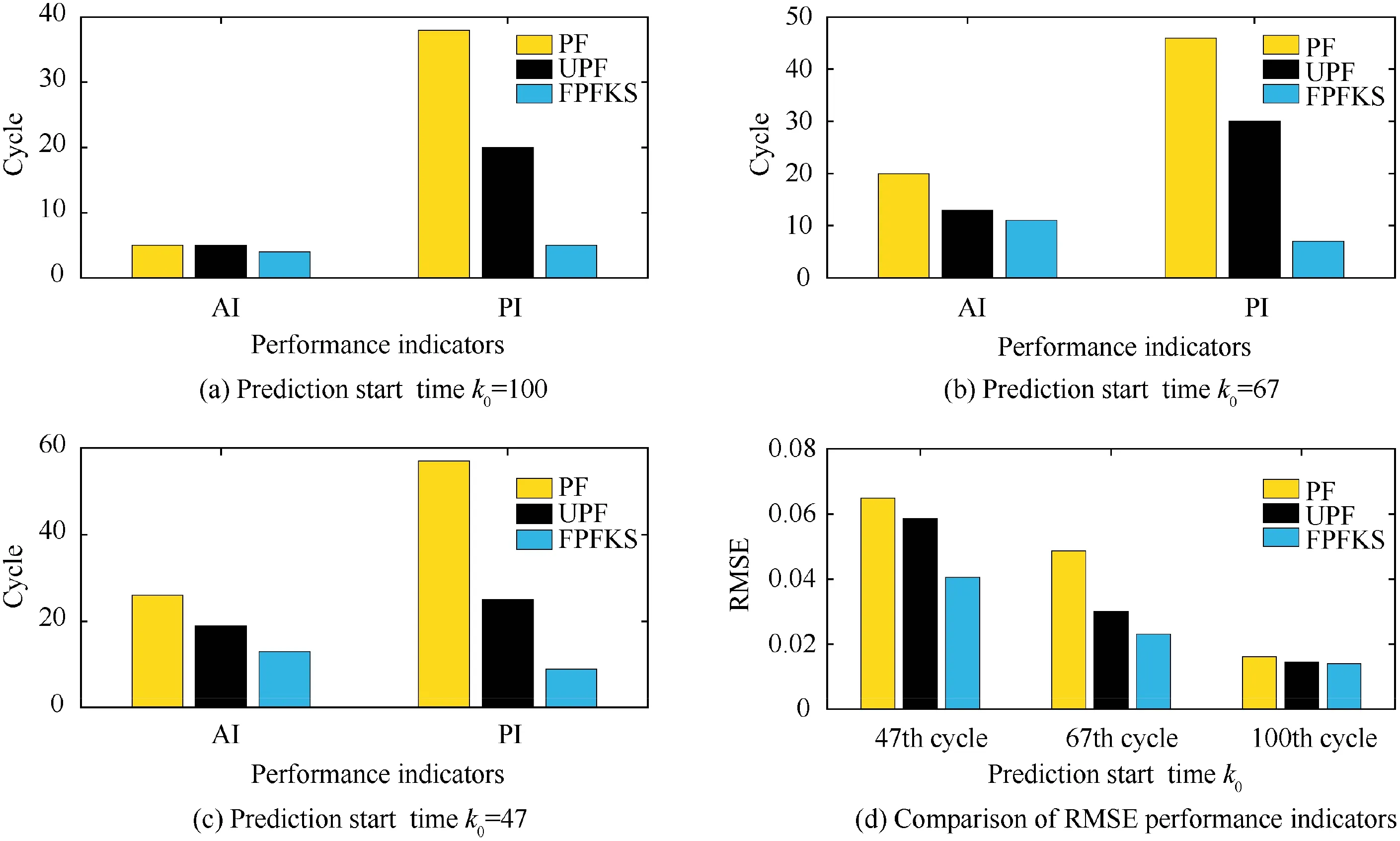
Fig. 6 Performance indicators comparison of RUL of B5 predicted by FPFKS, PF and UPF.

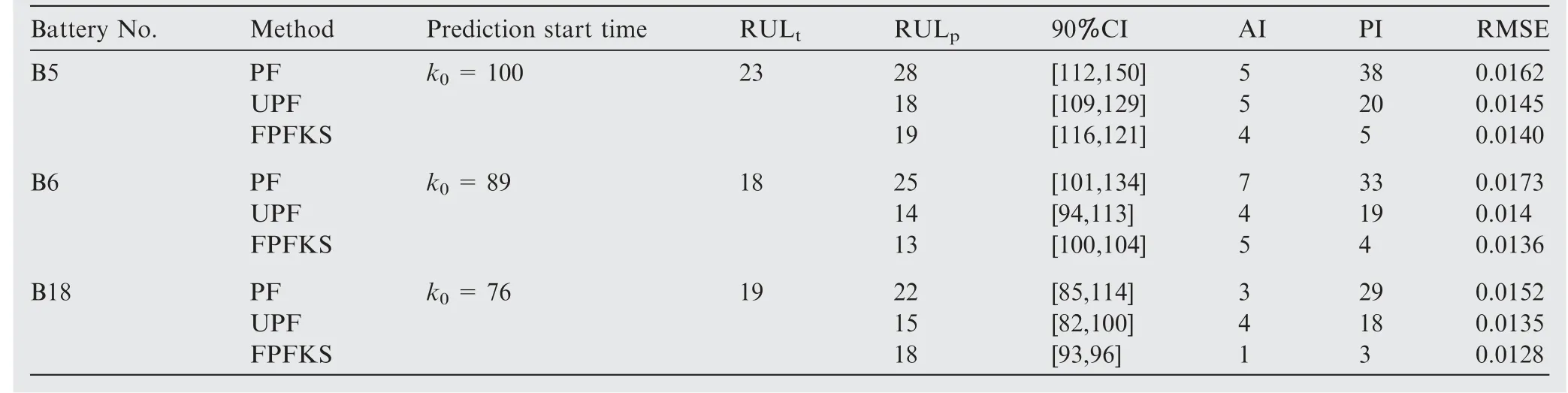
Table 3 RUL results of B5, B6 and B18 predicted by PF, UPF and FPFKS at approximately 80% of EOL.

Table 4 RUL results of B5, B6 and B18 predicted by PF, UPF and FPFKS at approximately 50% of EOL.

fidence interval for the RUL, and L CI is the lower bound of the 90% confidence interval for the RUL. U CI and LCI are determined based on the probability density distribution interval of the RUL.The upper bound of the 90%confidence interval is the number of the predicted RUL density distribution interval at the 95%position, and the lower bound of the 90% confidence interval is the number of the predicted RUL density distribution interval at the 5% position. xirepresents the n-step RUL prediction value, i=12,···n. And xsrepresents the true RUL value. The AI is the error between the predicted RUL and the actual RUL, reflecting the accuracy of the RUL prediction. The PI is the range of the 90% confidence interval for the RUL prediction, reflecting the precision of the RUL prediction and the credibility of the prediction. The RMSE reflects the accuracy of the capacity prediction throughout the prediction phase. It measures the extent to which the predicted capacity degradation trend fits the real capacity degradation trend.

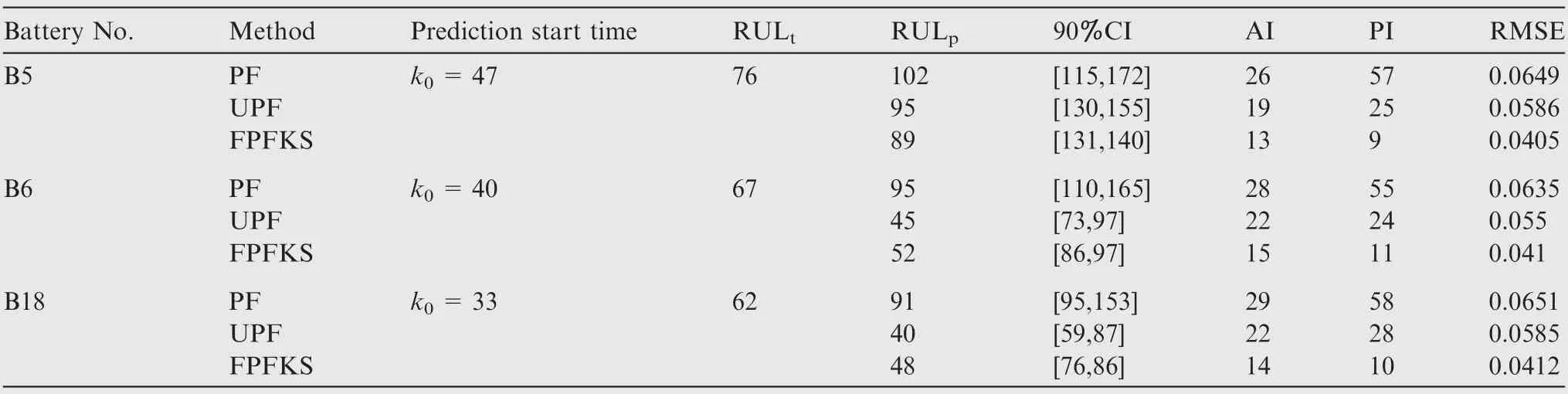
Table 5 RUL results of B5, B6 and B18 predicted by PF, UPF and FPFKS at approximately 35% of EOL.

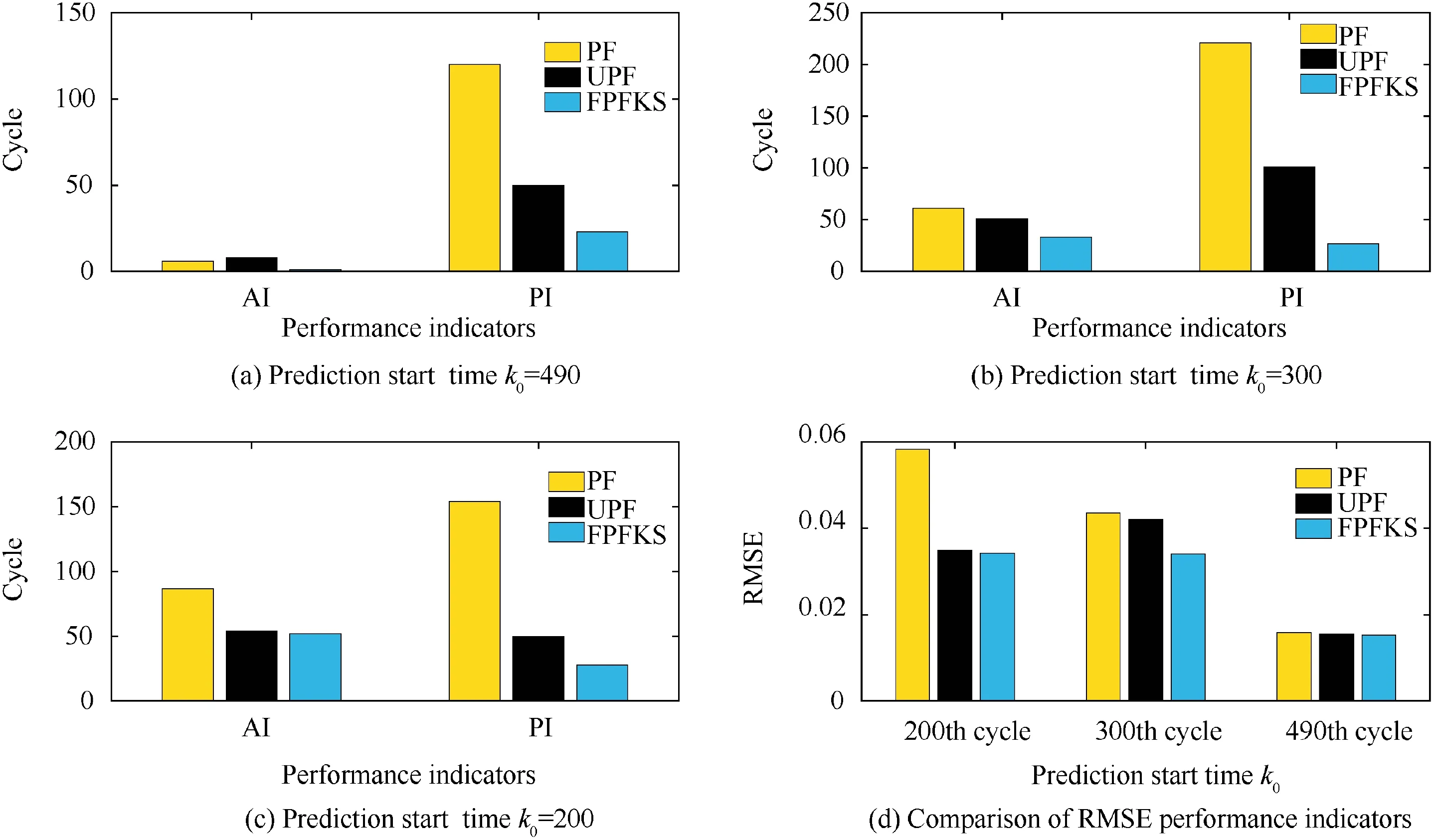
Fig. 7 Performance indicators comparison of RUL of RW4 predicted by PF, UPF and FPFKS.

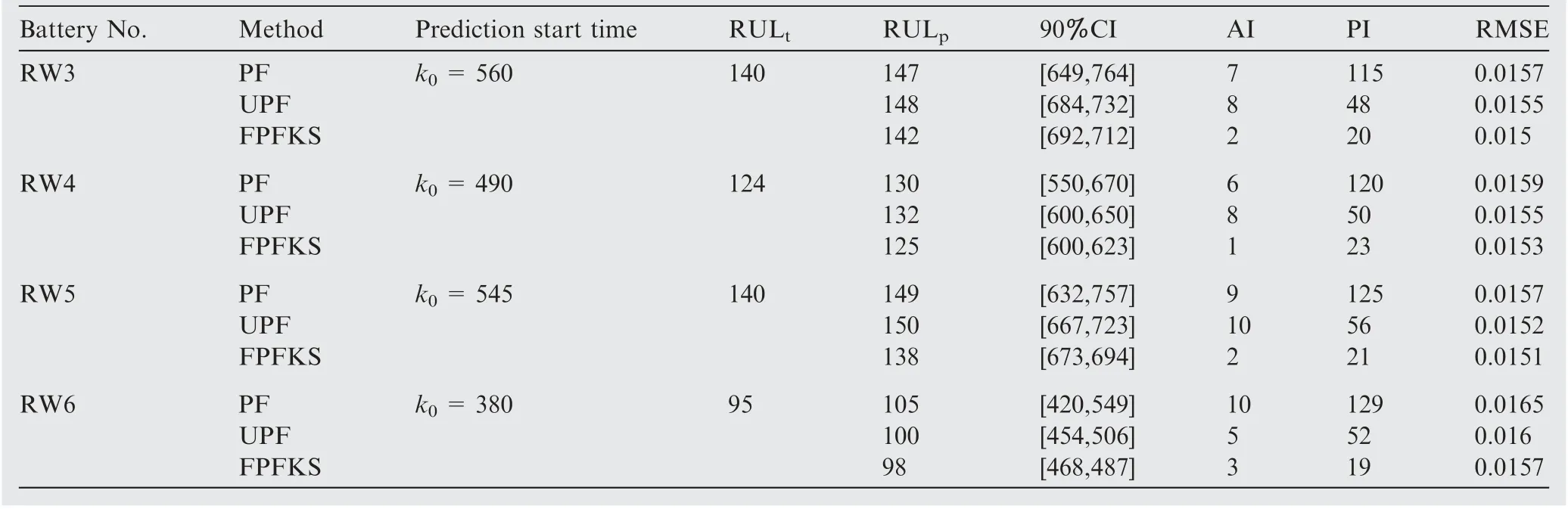
Table 6 RUL results of RW3, RW4, RW5 and RW6 predicted by PF, UPF and FPFKS at approximately 80% of EOL.

3.3. Comparative analysis of prediction results of FPFKS, PF and UPF

Compared with the PF-based prediction algorithm and the UPF-based prediction algorithm,the FPFKS-based prediction algorithm can dynamically update the particle weights in the prediction stage. And it guarantees the integrity of particle information and avoids particle degradation. To verify the superiority of FPFKS-based prediction algorithm,three methods are validated by using two NASA capacity degradationdata sets. For each set of data, the RUL predictions are approximately 80%, 50%, and 35% of the life cycle, respectively. The RUL prediction results of battery B5 are shown in Fig.5(a)-(c),The RUL prediction results of RW4 are shown in Fig. 5(d)-(f).

Table 7 RUL results of RW3, RW4, RW5 and RW6 predicted by PF, UPF and FPFKS at approximately 50% of EOL.

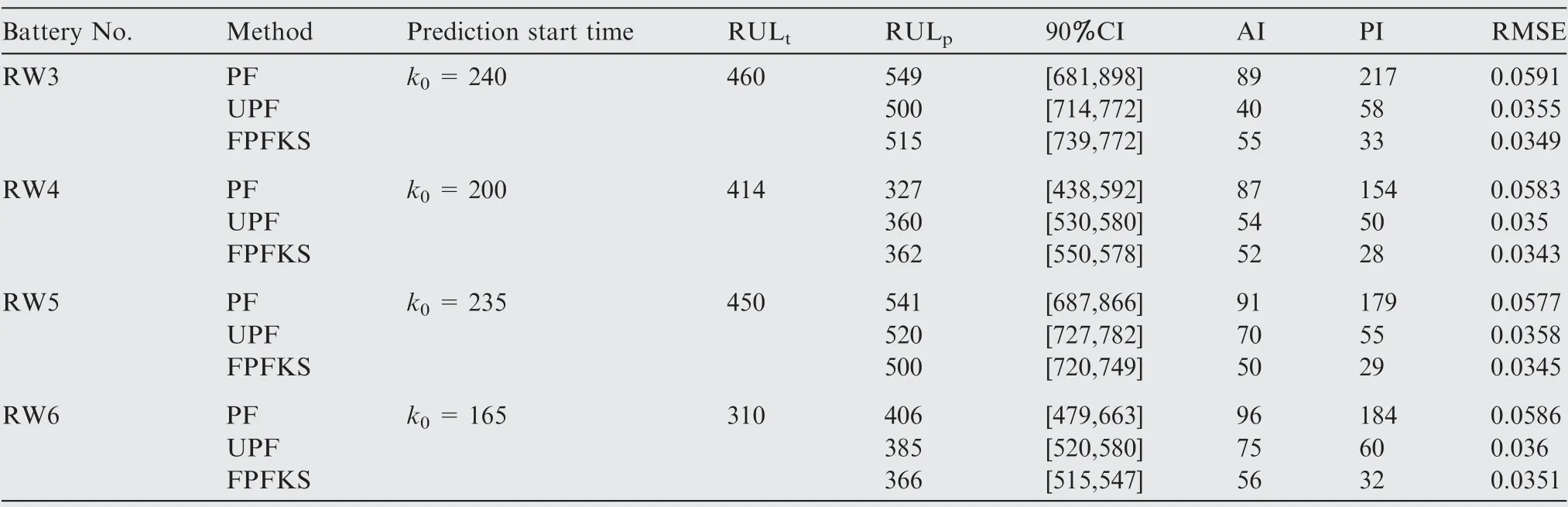
Table 8 RUL results of RW3, RW4, RW5 and RW6 predicted by PF, UPF and FPFKS at approximately 35% of EOL.

It can be observed from the prediction results that the FPFKS algorithm is compared with the PF algorithm and the UPF algorithm, and the RUL prediction result based on the FPFKS algorithm is closest to the true RUL, especially in the early RUL prediction. It explains that the prediction accuracy based on the FPFKS algorithm is highest. And the PDF of the RUL based on the FPFKS algorithm is narrowest and highest in height,which indicates that the effective samples based on the FPFKS algorithm are the best of the three methods, and the prediction results are the most concentrated and the prediction precision is highest. A comparison of the predicted performance indicators of the three methods is shown in Fig. 6. It can be observed from the figure that AI, PI, and RMSE predicted by the FPFKS algorithm are the smallest of the three methods, at different prediction start time, and the PI difference is the most obvious.It explains that the accuracy, precision and credibility of the prediction results of the FPFKS algorithm are highest. Moreover, in the prediction stage, the capacity predicted by the FPFKS algorithm is closest to the true capacity. The predicted capacity degradation trend corresponds to the real capacity degradation trend.The specific prediction performance indexes of Li-ion batteries B5,B6 and B18 at different prediction start time are shown in Table 3,Table 4 and Table 5.From the specific prediction performance indicators in the table,it can be inferred that the proposed method is superior to PF and UPF.

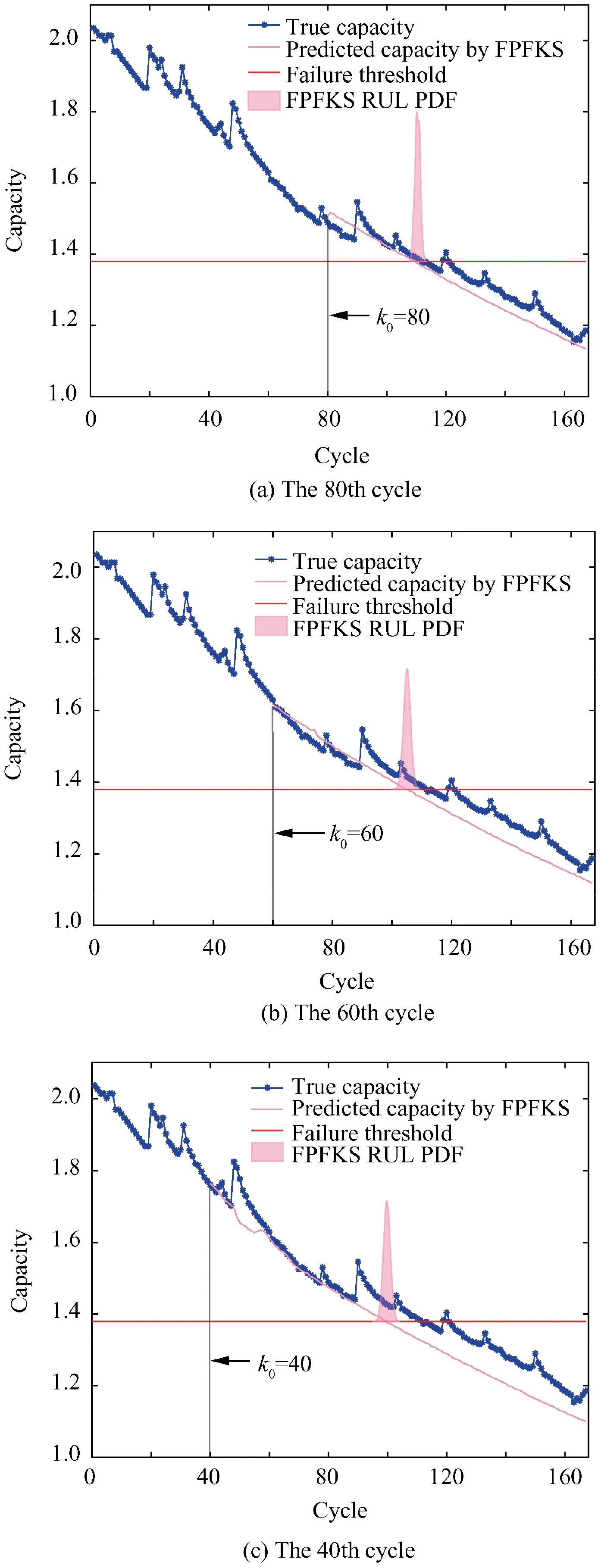
Fig. 8 RUL and RUL PDF results of B6 predicted by FPFKS.

The three methods were also validated by using RW discharging data sets.From Fig.5(d)-(f).It can also be observed from the prediction results that the FPFKS algorithm is compared with the PF algorithm and the UPF algorithm,the RUL prediction result based on the FPFKS algorithm is closest to the true RUL, and the width of PDF distribution based on the FPFKS algorithm for predicting the RUL is narrowest and highest. The comparison of the predicted performance indicators of the three methods is shown in Fig. 7. It can be observed from the figure that AI, PI, and RMSE predicted by the FPFKS algorithm are the smallest of the three methods at different prediction start time. The accuracy, precision, and credibility of the prediction results of the FPFKS algorithm are highest.And the predicted value of the capacity in the prediction phase is closest to the true value. It is shown that the FPFKS algorithm still has great advantages compared with the PF algorithm and the UPF algorithm when using random walk discharging data sets. The specific prediction performance indicators of the batteries RW3, RW4, RW5, and RW6 at different prediction start time are shown in Table 6,Table 7,and Table 8,respectively.From the specific prediction performance indicators in the table, it can be inferred that FPFKS is superior to PF and UPF.

3.4. Comparative analysis of prediction results between FPFKS and other two typical methods

This section compares FPFKS with a fusion prediction method (ND-AR RPF) and a data-driven approach (RVM+KF). Among them, ND-AR RPF is a fusion prediction method proposed by Liu et al.13. The ND-AR RPF prognostics technique employs ND-AR for observation series prediction and applies RPF to estimate the system state collaboratively. This method is a representative method for realizing the dynamic update of particle weights in the prediction process by constructing observations. RVM+KF is a data-driven approach proposed by Song et al.6. Song et al.used KF and physical degradation models to optimize RVM,and obtained good long-term prediction performance.

For the convenience of comparison, we use the same prediction conditions. That is, Li-ion batteries B5 and B6 were used to evaluate these three methods, the failure threshold of the Li-ion battery is 1.38 Ah, and the predicted start time is k0=40, k0=60, and k0=80, respectively.

The RUL prediction results of B6 based on the FPFKS algorithm are shown in Fig. 8. Here we use the AI and the width of PDF of the RUL (PDF width) as the predictive performance indicators.The comparison of the performance indicators of ND-AR RPF and FPFKS is shown in Fig. 9. At different prediction start time,the AI predicted by the FPFKS algorithm is smaller than that predicted by the ND-AR RPF algorithm, and the PDF width of the RUL is narrower than the ND-AR RPF algorithm. The specific prediction performance indicators for predicting the RUL of B6 at different prediction start time by using ND-AR RPF and FPFKS are shown in Table 9. It can also be observed from the table that FPFKS has some advantages in comparison with ND-AR RPF in terms of prediction accuracy and precision.

The comparison of RVM+KF and FPFKS prediction performance is shown in Table 10. The AI predicted by FPFKS is smaller than that predicted by RVM+KF. Especially when the prediction start time k0=60, the RUL of the Li-ion battery is predicted based on FPFKS to be closer to the true RUL, and the prediction accuracy is significantly higher than RVM+KF. And long-term prediction performance based on FPFKS is better than RVM+KF.

4. Conclusions and future work

This paper presents an FPFKS algorithm for the prediction of RUL of Li-ion batteries.The main contributions of this paper can be summarized as follows: (A) a new F-distribution PF and KS algorithm is proposed. Compared to PF, improved PF and some other typical prediction methods, the precision and accuracy of the prediction results are improved based on the method; (B) the applicability and robustness of the proposed method are good; (C) the computational complexity of the proposed method is low and it is suitable for online prediction.

In future studies, we will concentrate on how to reduce the uncertainty of the Li-ion battery cycle life prediction, and we need to evaluate the RUL prediction results of Li-ion batteries under more complicated working conditions.And we will consider transplanting the prediction algorithm to the embedded system for online RUL prediction to meet the actual engineering requirements.

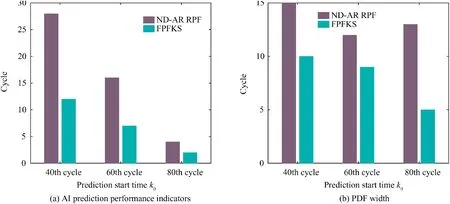
Fig. 9 Performance indicators comparison of RUL of B6 predicted by ND-AR RPF and FPFKS.

Table 9 RUL prediction results for B6 by ND-AR RPF and FPFKS.

Table 10 RUL prediction results for B5 and B6 by RVM+KF and FPFKS.

Acknowledgements

This work was co-supported by Aeronautical Science Foundation of China (No. 20183352030) and Fund Project of Equipment Pre-research Field of China (No.JZX7Y20190243016301).