Correlation-weighted least squares residual algorithm for RAIM
Dn SONG, Chung SHI, Zhipeng WANG, Cheng WANG, Guifei JING
a School of Electronic and Information Engineering, Beihang University, Beijing 100191, China
b Frontier Institute of Science and Technology Innovation, Beihang University, Beijing 100191, China
KEYWORDS Correlation analysis;Fault detection;Least squares residual (LSR)algorithm;Receiver autonomous integrity monitoring (RAIM);Slope
Abstract The Least Squares Residual (LSR) algorithm, one of the classical Receiver Autonomous Integrity Monitoring (RAIM) algorithms for Global Navigation Satellite System (GNSS),presents a high Missed Detection Risk (MDR) for a large-slope faulty satellite and a high False Alarm Risk (FAR) for a small-slope faulty satellite. From the theoretical analysis of the high MDR and FAR cause, the optimal slope is determined, and thereby the optimal test statistic for fault detection is conceived, which can minimize the FAR with the MDR not exceeding its allowable value. To construct a test statistic approximate to the optimal one, the Correlation-Weighted LSR (CW-LSR) algorithm is proposed. The CW-LSR test statistic remains the sum of pseudorange residual squares, but the square for the most potentially faulty satellite, judged by correlation analysis between the pseudorange residual and observation error, is weighted with an optimal-slope-based factor. It does not obey the same distribution but has the same noncentral parameter with the optimal test statistic. The superior performance of the CW-LSR algorithm is verified via simulation, both reducing the FAR for a small-slope faulty satellite with the MDR not exceeding its allowable value and reducing the MDR for a large-slope faulty satellite at the expense of FAR addition.
1. Introduction
Satellite navigation is widely used for civil aviation.Integrity is one of the required performances for GNSS, which is directly related to life safety.Receiver Autonomous Integrity Monitoring (RAIM) is one of the recommended method to evaluate GNSS integrity in user segment for aviation, which detects a faulty satellite via searching its observation bias in the pseudorange according to consistency check theory.1
The snapshot algorithm is the most widely used RAIM algorithm. There are two kinds of classical snapshot algorithms,namely,the Least Squares Residuals(LSR)algorithm2and the -Parity Vector (PV) algorithm.3Brown proved that LSR and PV are equivalent and are suitable for single faulty satellite detection.4Both of the two algorithms detect the faulty satellite via the binary hypothesis test, using the test statistic constructed in the measurement domain.
Many researchers are committed to improving the detection probability of faulty satellite using snapshot algorithms, i.e.,the probability of the test statistic exceeding the detection threshold. For example, Liu used the accumulated PVs for multiple epochs as the test statistic to improve the detection probability for minor observation bias,5and Sha further improved the detection probability by non-coherent processing for PVs of different epochs.6Ran combined PVs of accumulated epochs and the PV of a single epoch to improve the detection probability for both mutational and continuous observation bias.7Panagiotakopoulos improved the detection probability of faulty satellite by using the heavier tail distribution to model the observation error in snapshot RAIM algorithm under nominal mode, which is more accurate than the Gaussian distribution.8Sun proposed the leveraged method which can improve the fault detection and identification probabilities of the high leverage faulty satellite.9
It cannot be denied that the detection probability of faulty satellite is improved via the above test statistic reconstruction or modification methods. However, these methods ignore the original intention of RAIM, alerting Hazardous Misleading Information (HMI), the position error exceeding its allowable value,rather than the satellite fault.Because the position error and the test statistic for the snapshot algorithm are statistical independent,10the observation bias reflected by the large test statistic may bring a small position error, whereas that reflected by the small test statistic may bring a large position error. Actually, the position error and the test statistic are determined by two unrelated geometric characteristic parameters of the faulty satellite. Brown defined a parameter, named as the characteristic slope, using the ratio between these two parameters to qualitatively describe the relationship of the position error and the test statistic.11A faulty satellite with the large slope may cause high Missed Detection Risk(MDR),the probability of HMI when the test statistic is smaller than the detection threshold,for its observation bias bringing large position error and a small test statistic.Increasing the detection probability for a large-slope faulty satellite is necessary to decrease the MDR. In contrast, a faulty satellite with the small slope may cause high False Alarm Risk (FAR), the probability of the position error not exceeding its allowable value when the test statistic is larger than the detection threshold,for its observation bias bringing a small position error and a large test statistic. Increasing the detection probability for a small-slope faulty satellite will further improve the FAR,which is unacceptable for bringing observation resource waste.Therefore, pursuing high detection probability of faulty satellite is not applicable for all faulty satellites.
To ensure the integrity of navigation system, many researchers devoted to modifying the snapshot algorithms for reducing the probability of HMI,i.e.,the integrity risk.Hwang and Lee respectively proposed the NIORAIM method12and the Optimal Weighted Average Solution (OWAS) method13to weight the pseuodrange residuals in the test statistic of LSR algorithm. Both OWAS and NIORAIM can greatly reduce the protection level,which is related to the integrity risk caused by the largest-slope satellite among all of visible satellite, under the premise of slightly sacrificing positioning accuracy. The weights of the two algorithms are designed in the position domain and the measurement domain respectively.NIORAIM has been widely used, for example, Madonna applied the NIORAIM to the multi-constellation GNSS integrity monitoring in various phases of flight.14Joerger designed a Non-Least-Squares (NLS) detector, which can reduce the integrity risk in exchange for a slight increase in nominal position error.15Moreover, the advance RAIM algorithm is researched in the recent 10 years,16-19which can guarantee the integrity risk satisfying its requirement for the approach phase such as LPV-200.20
Because the MDR is the probability of HMI when the test statistic does not exceed the detection threshold, the above researches are all effective on reducing the MDR. However,these researches are all neglecting the FAR. There are a few researches focus on both reducing the MDR and the FAR.Fan proposed a slope-weighted LSR algorithm which can reduce both the MDR of a large-slope satellite and the FAR of a small-slope satellite,but neglected to reselect the detection threshold related to the distribution of the modified test statistic under the nominal mode.21Zhao et al.proposed a modified LSR algorithm based on the vertical critical slope, in which only the detection threshold is changed.1In this paper, we try to minimize both the MDR caused by a large-slope faulty satellite and the FAR caused by a small-slope faulty satellite under single-faulty-satellite mode in the LSR algorithm by reconstructing the test statistic. First, the performance of the LSR algorithm is theoretically analyzed for typical faulty satellites,considering the MDR and the FAR.The imaginary optimal slope is found during the analysis. Then, the optimal test statistic, related to the optimal slope, is designed to minimize FAR under the premise of MDR not exceeding its allowable value.Finally,the Correlation-weighted LSR(CW-LSR)algorithm is proposed. The pseudorange residual of the most potentially faulty satellite, which is decided by correlation analysis22between the pseudorange residual and observation error, is weighted with an optimal slope-related factor in the test statistic of the CW-LSR algorithm,making it approximate to the optimal test statistic. Moreover, the detection threshold in the CW-LSR algorithm is reselected to match the distribution of the correlation-weighted test statistic.The superior performance of the CW-LSR algorithm is verified compared to the LSR algorithm via mathematical simulations.
2. LSR algorithm performance analysis
The performance of the LSR algorithm is discussed with two factors, the MDR and the FAR. Both the MDR and the FAR can be theoretical calculated with the distributions of the position error and the test statistic, which are derived according to the geometry between the user and all visible satellites, abbreviated as ‘‘geometry”, and the distribution of the observation error.
2.1. Distribution of position error
According to the pseudorange position principle,the linearized observation equation between the receiver and the visible satellites is as follows:





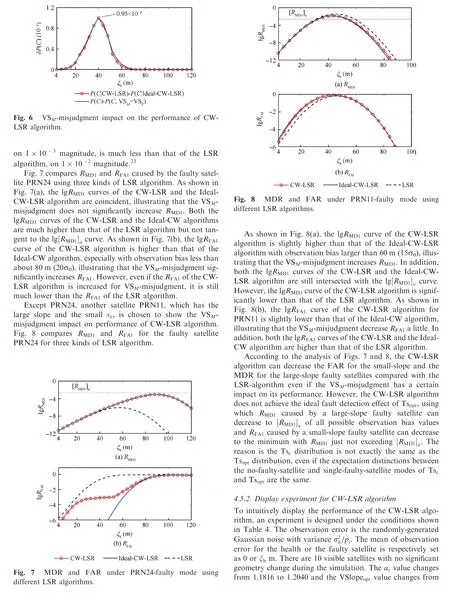

Table 4 Simulation conditions for the CW-LSR algorithm display experiment.
Figs. 9 and 10 respectively show the simulation results setting PRN 2 and PRN 29 as the single faulty satellites. In the two figures, Figs. 9(a) and 10(a) present the VPE, and Figs. 9(b)and 10(b)present the ratio of the test statistic to the detection threshold, notated as Ts/Td.
As shown in Fig.9(a),the injected bias on the pseudorange of PRN2 brings little change in the VPE. As shown in Fig. 9(b), the injected bias significantly increases the Ts/Td value to much larger than 1 for the LSR algorithm at each epoch,which means RFA1reaches 100% using the LSR algorithm within the bias injection duration. However, the injected bias causes little change in the Ts/Td value for the CW-LSR algorithm, which means RFA1remains at 0. Therefore, the false alarm caused by PRN2 with 60 m (15σ0) observation bias is avoided using the CW-LSR algorithm.
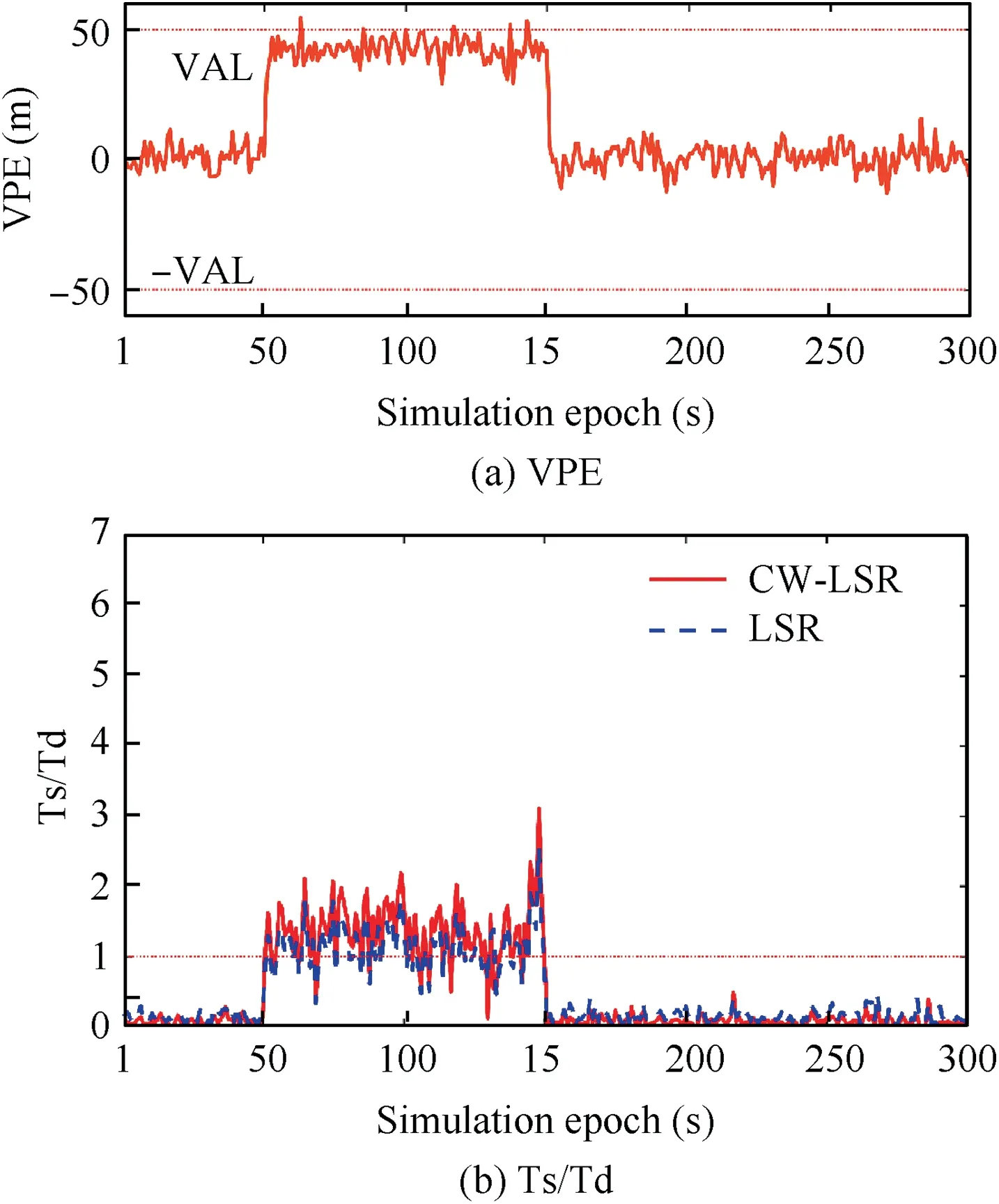
Fig. 10 VPE and Ts/Td for PRN 29.
As shown in Fig. 10(a), the injected bias on the pseudorange of PRN29 significantly increases the VPE, exceeding VAL in some epochs. As shown in Fig. 10(b), the epochs of Ts/Td <1 for the CW-LSR and LSR algorithms are 18 and 38 respectively, which illustrates that RMD1of the CW-LSR algorithm is lower than that of LSR algorithms. This simulation result verifies that RMD1caused by a large-slope faulty satellite can be decreased using the CW-LSR algorithm compared with using the LSR algorithm.
Figs. 9 and 10 visually display the superior performance of the CW-LSR algorithm.Both the RMD1caused by a large-slope faulty satellite and the RFA1caused by a small-slope faulty satellite using the CW-LSR algorithm are lower than those using LSR algorithms. The consistency between the VPE and the test statistic is significantly improved using the CW-LSR algorithm rather than the LSR algorithm.
It should be mentioned that the CW-LSR algorithm is designed considering only the VPE.For the application of considering horizontal positioning error,the parameters related to the direction in Tscand Tdcshould be rotated from vertical to horizontal.
5. Conclusions
The CW-LSR algorithm is proposed in this paper to reduce the MDR caused by a large-slope faulty satellite and the FAR caused by a small-slope faulty satellite under the singlefaulty-satellite mode. The test statistic of the CW-LSR algorithm, Tsc, is constructed using the sum of pseudorange residual squares.The square of the most potentially faulty satellite,judged by correlation analysis between the pseudorange residual and observation error,is weighted with a parameter related to the optimal slope. Tscis theoretically proved to have the same non-central parameter with the optimal test statistic Tsopt, which can minimize the FAR under the premise that the MDR does not exceed its allowable value. The superior performance of the CW-LSR algorithm is verified via mathematical simulations. This algorithm can reduce the FAR caused by a small-slope faulty satellite under the premise that the MDR not exceed its allowable value and can reduce the MDR caused by a large-slope faulty satellite at the expense of FAR addition compared with the LSR algorithm.
Acknowledgements
This study was co-supported by the National Natural Science Foundation of China(Nos.41804024,41804026)and the Open Fund of Shaanxi Key Laboratory of Integrated and Intelligent Navigation of China (No. SKLIIN-20190205).
Appendix A. Correlation coefficient between the residual vector and the observation error
The correlation coefficient between the residual vector and the observati on error for VSi,notated as,is defined as follows23
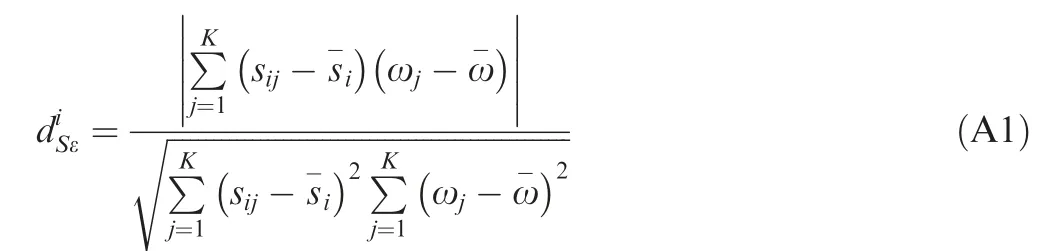
Appendix B. Derivation of the non-central parameter for B
With the assumption that VSmis the faulty satellite and its observation bias is ξb, the pseudorange residual of VSmis as follows:
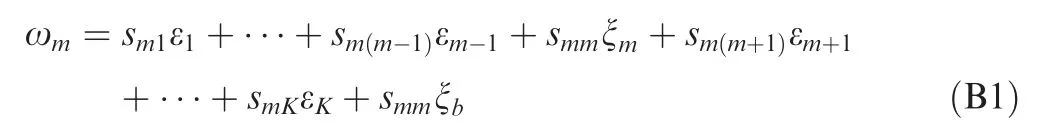
In Eq.(B1),εm=ξm+ξb,where the observation error εmof VSmincludes the observation noise ξmand the observation bias ξb. By setting ωno=sm1ε1+···+smm-1()εm-1+smmξm+smm+1()εm+1+···+sKεK,ωnois equal to ωmwith no faulty satellite. Substituting ωnointo Eq. (B1), ωmcan be simplified as

Therefore,
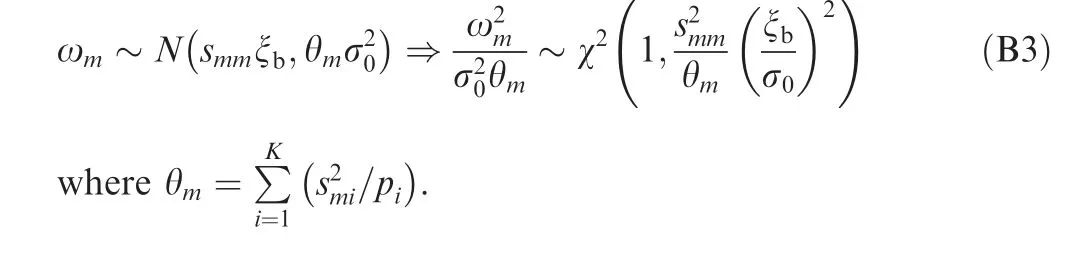
 CHINESE JOURNAL OF AERONAUTICS2020年5期
CHINESE JOURNAL OF AERONAUTICS2020年5期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Experimental of combustion instability in NTO/MMH impinging combustion chambers
- Three-line structured light vision system for non-cooperative satellites in proximity operations
- Remaining useful life prediction of aircraft lithium-ion batteries based on F-distribution particle filter and kernel smoothing algorithm
- Flow characteristics around airfoils near transonic buffet onset conditions
- Experimental investigation of flow and distortion mitigation by mechanical vortex generators in a coupled serpentine inlet-turbofan engine system
- An improved prediction model for corner stall in axial compressors with dihedral effect
