一“估”到“底”

陈妍璐

《数学课程标准》指出：“数学教学活动，特别是课堂教学应激发学生兴趣，调动学生积极性，引发学生的数学思考，鼓励学生的创造性思维;要注重培养学生良好的数学学习习惯，使学生掌握恰当的数学学习方法。”“学生学习应当是一个生动活泼的、主动的和富有个性的过程。除接受学习外，动手实践、自主探索与合作交流同样是学习数学的重要方式。”结合以上理念，笔者试图在低年级课堂上培养学生的估算意识，进而促进学生数感的形成。

一、问题的提出

1.估算。估算，即大致推算，是对事物的数量或算式的结果作出的大概推断，是计算能力的重要组成部分。不同于精确计算，它是在不进行精确测量和计算的情况下作出的判断，对原始数据的精确性没有过高的要求，一般只需要口算就能得出大致结果，所以相对于精确计算，它更便捷。正因为这种优势，被广泛应用于人们生活和学习中，有着不可替代的优势。

2.数感。数感是对数与运算的一般理解，可以帮助人们用灵活的方法作出数学判断，并对解决复杂问题提出有效的策略。数感作为一种数学素养，是一种主动、自觉、自动化的理解和运用数及运算的基本能力。估算能力的培养有利于学生摆脱繁琐的计算，进而思考数量关系的内部联系，逐步形成稳定的数学思维能力。

3.估算与数感。估算虽是大概的推算，却包含了观察、实验、猜测、推理、计算等诸多的数学活动，是一系列数学活动的集中体现，极大地丰富了数学的学习，有利于提升孩子的数感。

二、估算教学的现状

估算在问题解决上降低了计算的要求，对学生数感的形成有着不可替代的作用，但估算教学的现状却不容乐观，简单罗列如下：

1.精确计算被特别优待。实际教学中，因为数学追求准确的学科性质，精确计算在应用时被特别优待。

例如：在（  ）里填“>”“<”或“=”。32×8（  ）45×12

对所教班级的121个孩子进行了实验，选择准确计算的有87位，占72%，其中正确的有83位，正确率为95%。选择估算的有32位，占26%，正确的有28位，正确率为87.5%;有2位无效。

从样本数据上看，绝大部分孩子看到题目以后首先想到的是计算，这样确实是保证了较好的正确率。只有小部分孩子选择了估算，他们将32×8估成30×8=240，45×12估成45×10=450，大小一目了然。

虽然两种处理都能得出结论，但是估算避免了繁琐的计算。在估算的过程中经历了取近似数、整十数乘法的计算、数的大小比较，较之准确计算包含了更多的数学思考，更好地提升了孩子数学学习的能力。相比之下，准确计算只需要计算即可，很多孩子舍近取远选择了机械计算，也失去了对算式中内部关系的思考机会。

2.估算有风险，舍近求远。从短期的效果来看，精算更具诱惑。估算的过程稍显复杂，所以有不少孩子即便掌握了估算的方法，还会出现反复。每隔一周，着手对相同类型的题进行了实验。情况如下：第2次实验选择精算的占59.5%，选择估算的占38%，而正确率分别为98%和90%。第3次实验 选择精算的占35.5%，选择估算的占62.8%，而正确率分别为98%和98%。

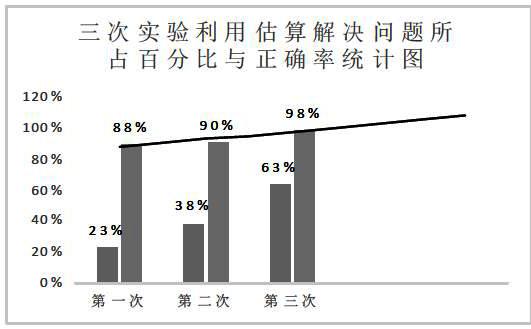
多次方法比较，学生逐渐感受到了估算的简便，越来越多的孩子重新作出选择，估算的熟练程度和水平也日渐提升。比较三次试验，对选择估算人数所占百分比和各自的正确率进行了分析如下：

反复比较，估算的优势也逐渐在学生的头脑中扎下了根。可喜的是估算的正确率也逐渐提升了，让估算教学有了继续下去的信心。估算的意识强了，学生有更多的精力思考数量之间的关系，数与数之间的关系，数学的敏锐感觉上来了，数感也就来了。

3.对估算的错误理解。估算，顾名思义先估后算，在运用中却又经常被理解成先算后估取近似值。例如：西瓜每箱48元，张叔叔要买4箱西瓜，大约需要多少钱？

不少孩子首先想到48×4=192（元），再将192估成190。得出的结果看似估算，其实是一个近似值。估算的正确步骤是先“估”再“算”，先对繁杂的数据简化处理，再计算，而非先“算”再“估”，先精确计算再取近似值。

4.单纯、孤立地教学估算，没有建立知识间的联系。因为对估算价值的错误定位，将精确计算作为解决数学问题的主力，简单粗暴地对待问题。即便要求估算，很多教师也只是为了教而教，教学上以强调估算的方法为主，忽视引导孩子产生估算意识。没有解决“为什么要估算”“什么情况可以估算”“为什么这么估算”等问题，不利于培养孩子的估算意识。

三、估算意识的培养

1.解题方法的比较，培养孩子的估算意识。估算的魅力在于“估”，重在对准确数据的加工，减轻了计算的繁琐。比如：

甲城到乙城三种不同火车的票价如下表：

吴老师买3张同样价格的火车票，付给售票员1000元，他买的是哪一种？（先估算，再在正确的答案旁边画√。）

不少学生读完题迅速写出算式埋头计算，而选择估算的孩子几乎是脱口而出。两种结论看似相同，但其中经历的思考却截然不同。选择精算的学生在计算上颇为麻烦，毕竟刚刚涉及多位数的乘法计算，一是三道算式较费时间，二是稍有不慎就会出现失误。虽然得出了结论，但是费时费力不够简洁。

第二种方法重在思考，对计算的要求不高，学生只要对数量进行加工，口算就行，结论呼之而出。两种方法的差别就是“估”和“算”的先后问题，优势一目了然。有了比较就有了重新的选择，就是因为这些比较让孩子们明确估算的重要价值，也因此催生了孩子的估算意识。

2.对结论的合理性判断。《教学课程标准》指出：“学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。”

数学不只是计算，更多的是对数量之间联系的观察、猜测、推理、验证。计算结论是否合理，过分依赖精算，思维往往因计算的繁琐而搁浅。把课堂的主动权交给学生，提供足够的机会让孩子充分表达自己的想法，让学生巧用估算，快速估量，在思辨中对结论的合理性作出理性的判断。

比如：一年级和二年级学生到剧场看演出，一年级有195人，二年级有198人。剧场共有400个座位，够坐吗？为什么？

有孩子这样列式：195+198=493（人）检查时，他并没有计算就发现了错误，在问及原因时，她说：“195比200少，198也比200少，所以结果应该比400少。”合理的推算、估算让数学活动更加简洁而富有实效，估算的价值应运而生。

3.解题方式的多样化。可以用估算的方法解决问题的题型很多，较为典型的有大小比较、判断题、选择题等等。在讲授此类题型时选择合适的方法往往能节省时间，减少计算量，甚至更能让孩子们理清数量之间的关系。从题海中解放出来，站在形成解题策略的高度看待每一类题型有利于培养智慧型的学生。

估算既是一种技能更是一种意识。在数学课堂中，教师应该着手加强学生估算方法的训练，应该让学生体验估算的意义和价值，让孩子们产生估算的意识，进一步增强他们在具体情境中利用估算解决问题的能力。在更加丰富的数学活动中，让孩子经历猜想、估计、计算、验证、试验、推理等更加丰富的思维历程，让数学更加有血有肉，有根有據，有因有果。