高能点火稀薄混合气初期火核发展的数值仿真研究

马鹏飞，李铁，2 ，黄帅，谢思瑜，依平

(1.上海交通大学海洋工程国家重点实验室，上海 200240；2.上海交通大学高新船舶与深海开发装备协同创新中心，上海 200240)

火花点火发动机采用稀薄燃烧可提高热效率并降低有害排放[1-4]，然而，稀薄燃烧火焰发展速度慢，循环负荷变动大[5]。增强缸内湍流可提高火焰发展速度，但会增加火花点火不稳定性。为了解决稀薄混合气点火问题，需要对火花点火过程进行研究。有学者提出了基于增加点火能量的新点火策略，如电流增强火花点火[6]、多线圈多火花放电[7]、双线圈连续放电[8]等，且利用试验对其进行验证。

由于点火在一个极小的空间内发生，在发动机仿真中，通常不涉及点火过程的详细计算，这显然不利于研究点火策略对稀薄混合气初期火核发展的影响。

国外早在20世纪就有关于点火仿真建模的研究。Herweg与Maly[9]提出了火核形成与发展的一维欧拉模型，并进行了试验验证；LI (Laminar Ignition)模型[10]可以计算低湍流且无对流条件下的点火情况，而SKI (Small Kernel Ignition)模型[11]则考虑对流条件下的点火过程。但是，一维欧拉模型计算结果具有高网格灵敏度，且无法提供准确的初期火核信息。利用拉格朗日模型，则可以将点火模型与其他如流场及燃烧等欧拉模型分离，在子网格尺度上对初期火核进行更详细的计算。其中，DPIK (Discrete Particle Ignition Kernel)模型[12]以在火花塞周围球形分布的粒子代表初始火核信息，并未考虑点火电路模型。AKTIM (Arc and Kernel Tracking Ignition Model)模型[13]以沿火花路径均匀分布的一组粒子代表初始火核，根据电路详细信息计算火核膨胀发展。ISSIM (Imposed Stretch Spark Ignition Model)模型[14]是AKTIM模型的改进版，依据火焰表面密度传输方程计算初始火核及火核后续发展。Spark-CIMM模型[15]则基于Karlovitz数判断初始火核的位置，且与G方程结合计算燃烧过程。Tommaso等[16]提出的模型详细考虑了火核及等离子通道的发展过程，可模拟再击穿等现象。Kinoshita等[17]提出的模型根据电极之间的电场信息模拟等离子通道形状发展并据此初始化燃烧计算。VTF (Virtual Thermal Fluids)点火模型[18]亦是基于AKTIM模型，与SAGE燃烧模型相结合，该模型考虑了点火系统的所有设计参数。

目前，国内研究多集中于点火能量影响的试验研究[19-20]，而点火过程的详细仿真研究较少。初期火核的形成与发展对稀燃发动机负荷变动有重要影响，因此有必要开展对点火过程的详细仿真研究。

本研究采用一维拉格朗日模型，利用OpenFOAM编写代码，发展击穿电压拟合公式，探究点火能量对稀薄混合气初期火核形成的影响，旨在为后续点火过程影响发动机负荷变动机理研究提供支撑。

1 点火模型

1.1 电路子模型

火花塞放电过程可分为击穿、弧光和辉光3个阶段。其中，击穿与弧光阶段仅持续几十微秒，本点火模型不考虑该过程细节，仅为后续辉光阶段提供初始参数。

为了计算初期火核的初始半径与温度，需要计算击穿能量。击穿能量可由简化的AKTIM模型基本方程[21]算出：

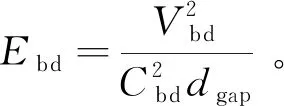
(1)

式中：dgap为火花塞间隙；Vbd为击穿电压，通常由Pashley公式给出[21]；Cbd为模型常数。

Pashley公式根据低压条件下的试验数据拟合得出，而现代增压发动机点火时环境压力远高于Pashley公式适用范围，导致其计算结果与试验差距较大。本研究试验发现当环境压力高于1 MPa时，击穿电压是环境压力的非线性函数，并发展了新的击穿电压公式[22-23]：

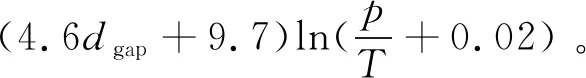
(2)

式中：p为环境压力；T为环境温度。

辉光放电过程中，次级线圈将能量传递至初始火核，以支持火核进一步发展。火花塞电极处功率可由火花塞间隙瞬时电压Vs(t)与次级线圈瞬时电流Is(t)计算：

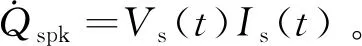
(3)

1.2 火核发展子模型

假设击穿阶段后火花塞间隙处形成一球形初始火核，其温度Ti与半径ri分别为

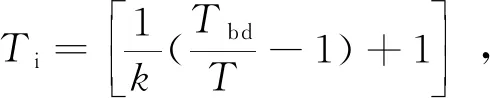
(4)

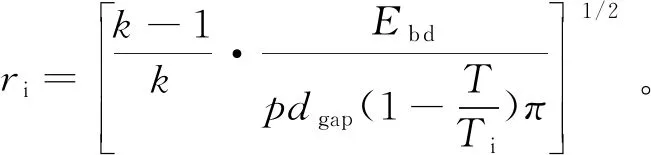
(5)

式中：k为未燃气体比热容比；Tbd为击穿温度。

在求解质量守恒方程时，考虑了湍流对初始火核的影响，如式(6)：

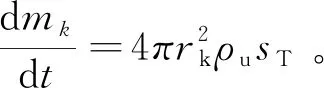
(6)

式中：ρu为未燃气体密度。初始火核半径rk由下式计算：

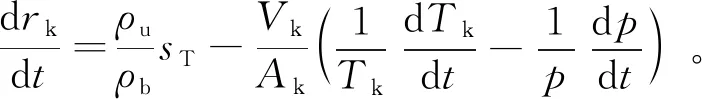
(7)

式中：ρb为已燃气体密度；Ak为火核表面积；Vk为火核体积。湍流火焰速度sT由层流火焰速度su与火核位置处的火焰褶皱Ξ得出：

sT=Ξsu，

(8)

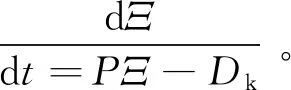
(9)

式中：P与Dk分别为ECFM燃烧模型中的源项与耗散项[13]，并采用单步甲烷燃烧反应。

初始火核的温度分布可以分为两种状态。当火核中心温度高于绝热火焰温度Tad的3倍时，从火核中心处至未燃混合物之间的热传导不能忽略，可通过式(10)求解热传导方程计算火核内部温度分布：

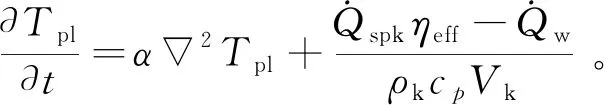
(10)

式中：ηeff为能量传递效率。电极处热传导损失可由下式计算：

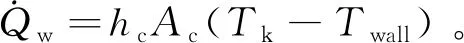
(11)

式中：hc为火花塞电极处的对流系数；Ac为火核与火花塞电极接触面积；火核温度Tk为火核内部温度的均值，并假设电极温度与电极附近壁面温度Twall相同。

在子网格中求解式(10)，初始条件为

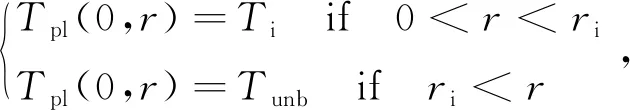
(12)

边界条件为

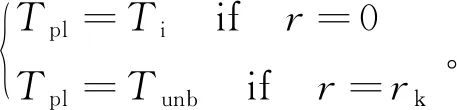
(13)

当Tk<3Tad时，化学反应和电路之间的热传递对火核的发展影响占据主导地位，此时可假设火核内部温度均匀分布，火核温度可由下式进行计算：

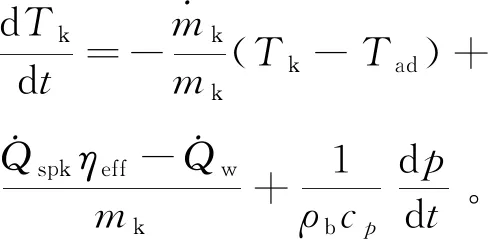
(14)

1.3 几何模型与网格

图1示出试验所用火花塞模型及计算网格，对火花塞电极间隙局部网格进行了加密处理，网格数共102 876，火花塞电极间隙为0.82 mm。

图1 火花塞模型及计算网格

2 试验装置

试验装置见图2，包括定容燃烧弹、预混容器、可变策略点火系统和高速纹影成像系统等。

试验过程中，甲烷与空气先在预混容器中混合均匀后充入定容燃烧弹。达到预定压力后，控制系统发出点火信号，同时利用高速纹影法记录初期火核形成与火焰传播过程。相机拍摄频率为100 000 帧/s，曝光时间1 μs。使用Tektronix P6015A高压探针和Tektronix TCP0030A电流钳分别测量火花塞电极两端放电电压和次级线圈电路电流。

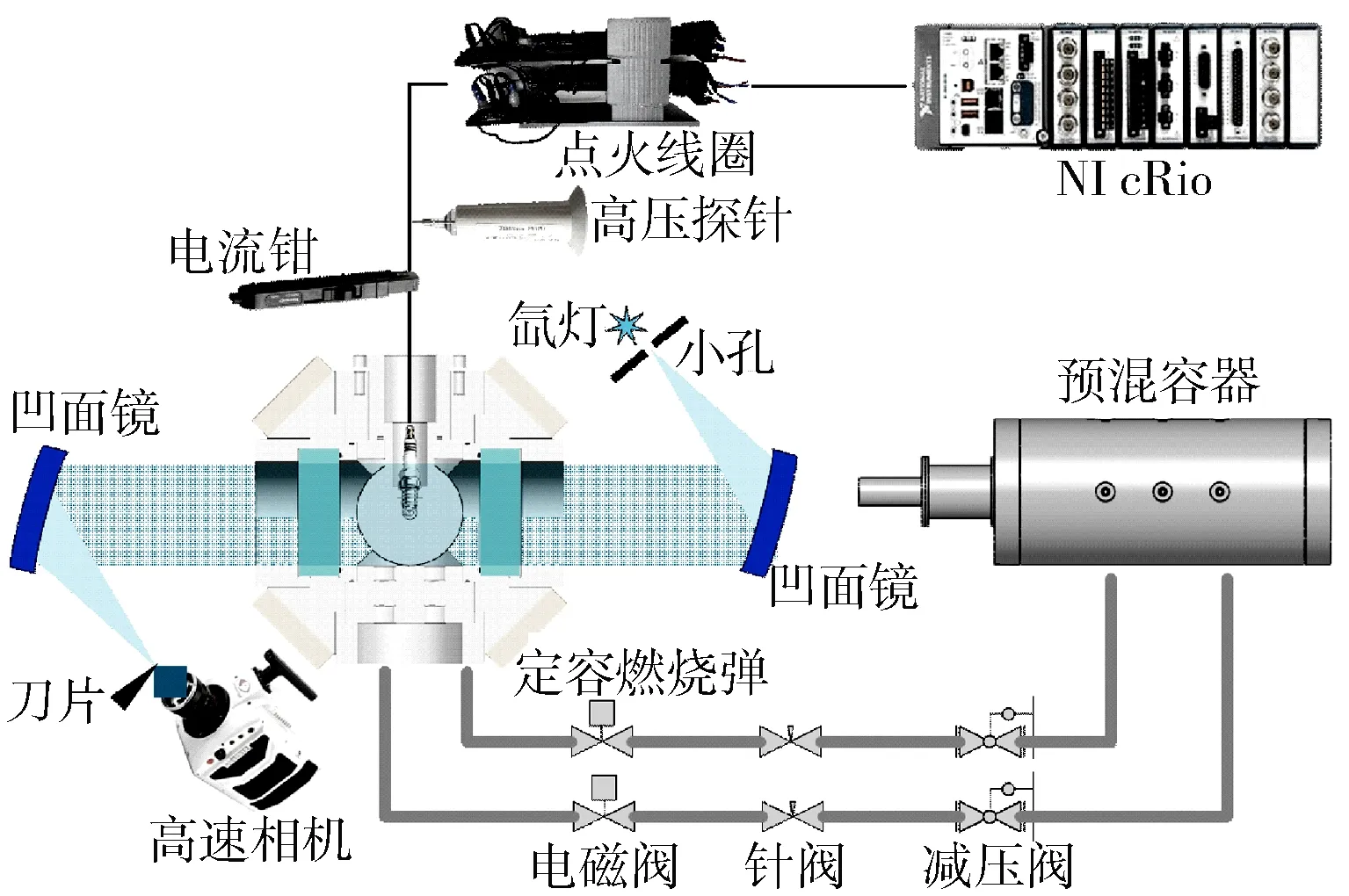
图2 试验装置示意

点火系统由并联点火线圈和NI CRIO-9036内部控制器组成，且每个线圈都可以由NI CRIO-9036控制器独立控制，以达到改变点火策略的目的。点火系统电路见图3。

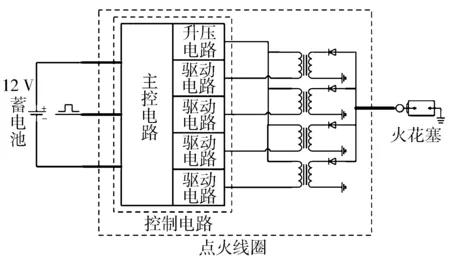
图3 点火线圈电路

3 结果与讨论

3.1 模型常数的标定

在式(1)中，击穿能量以经验公式给出，一般来说模型常数Cbd在150～250 kV·J-1/2·mm-1/2之间取一定值[21]。按照该范围选取模型常数计算的击穿能量最大值(Cbd=150 kV·J-1/2·mm-1/2)是最小值(Cbd=250 kV·J-1/2·mm-1/2)的2.78倍，计算所得火核初始半径亦相差较大；且若考虑点火策略对击穿能量的影响，上述范围并不完全适用。因此对该模型常数的重新标定是必要的。

在击穿瞬间记录击穿电压与击穿电流，将其乘积积分后可得击穿能量。在不同环境压力下，采用不同点火策略时的击穿能量结果见图4。从图4可以看出，同一压力下，增加并联线圈数，击穿能量随之增加，且在高压下尤为明显。由式(2)计算所得击穿电压与点火策略并不相关，为确保击穿能量计算准确，不同策略下，模型常数Cbd应取不同数值，如表1所示。

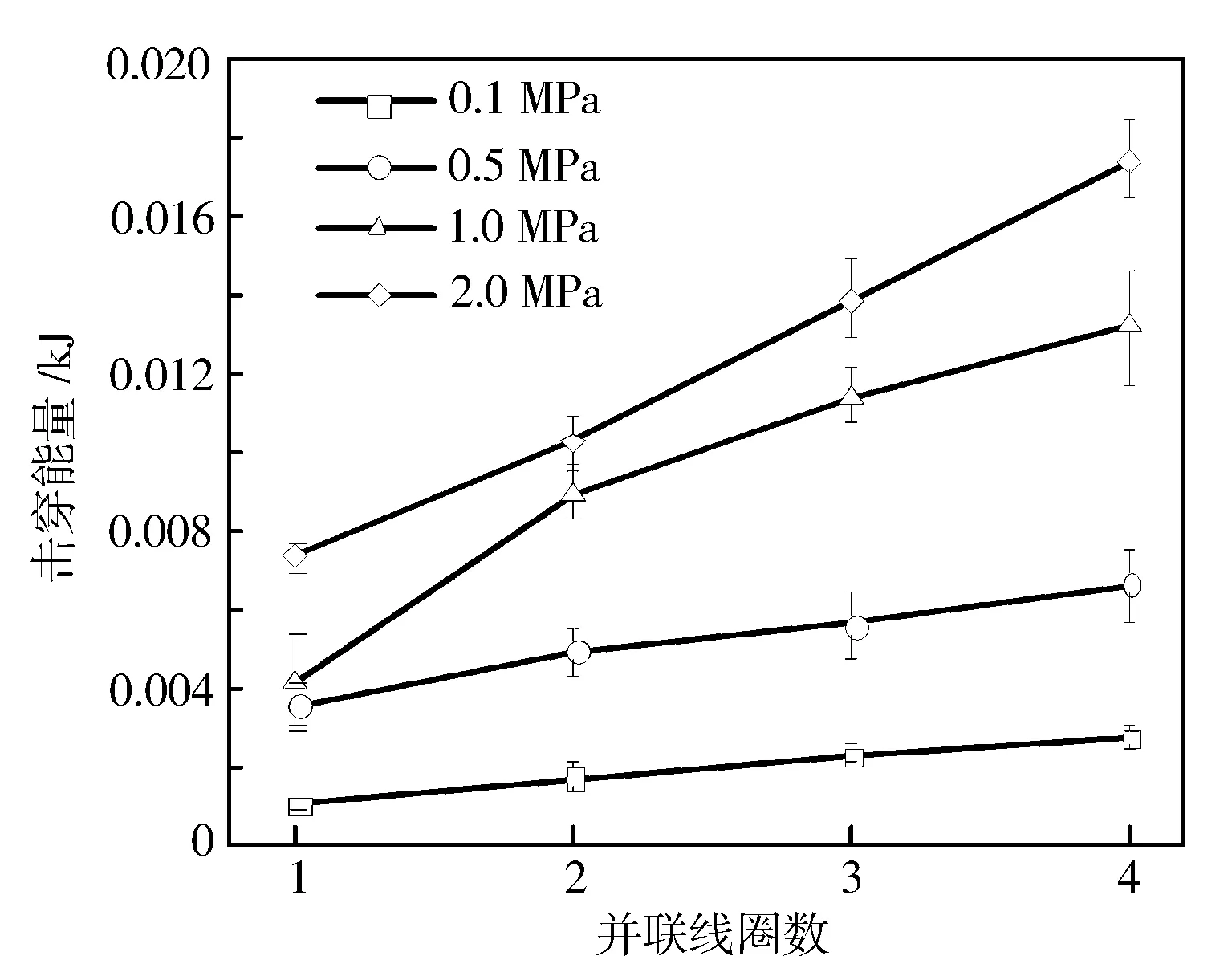
图4 击穿能量标定结果

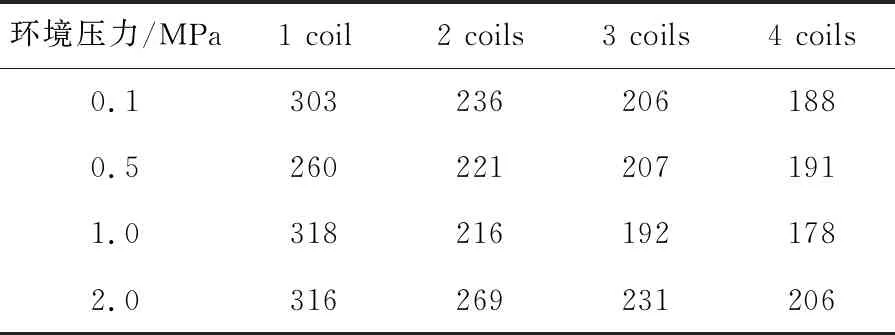
表1 模型常数Cbd取值 kV·J-1/2·mm-1/2

3.2 过量空气系数φa的影响

以击穿瞬间为0时刻，φa=1.51时，试验与仿真初期火核发展见图5。从图5可以看出，仿真能较好地再现试验观测的初期火核发展。混合气浓度相同时，低压下初期火核发展更快。放电持续期为2 ms，在2 ms内，环境压力分别为0.5 MPa与1 MPa时火核大小较为接近。初始火核基本呈球形，在发展的过程中受到火花塞的影响而逐渐呈椭球形。

图5 试验与仿真结果对比

将火焰纹影图像二值化去除背景后计算其面积，即为沿光路方向的火焰投影面积，根据该面积计算火焰的等效半径；仿真中的火核半径等于火花塞电极中心截面处火核面积(与试验同方向的投影面积)对应的等效半径。各个环境压力下初期火核半径发展对比见图6。在试验与仿真中，均使用单线圈点火。

击穿发生后，初始火核在火花塞电极中心产生，并迅速增长。试验发现，0.5 ms之前火核增长速度较快，这可能是由于在击穿和弧光过程中等离子体通道温度较高的缘故，此时火核增长速度主要由线圈释放能量以及热传导控制。0.5 ms之后火核增长逐渐变缓，此时火核增长速度主要受自身化学反应控制。

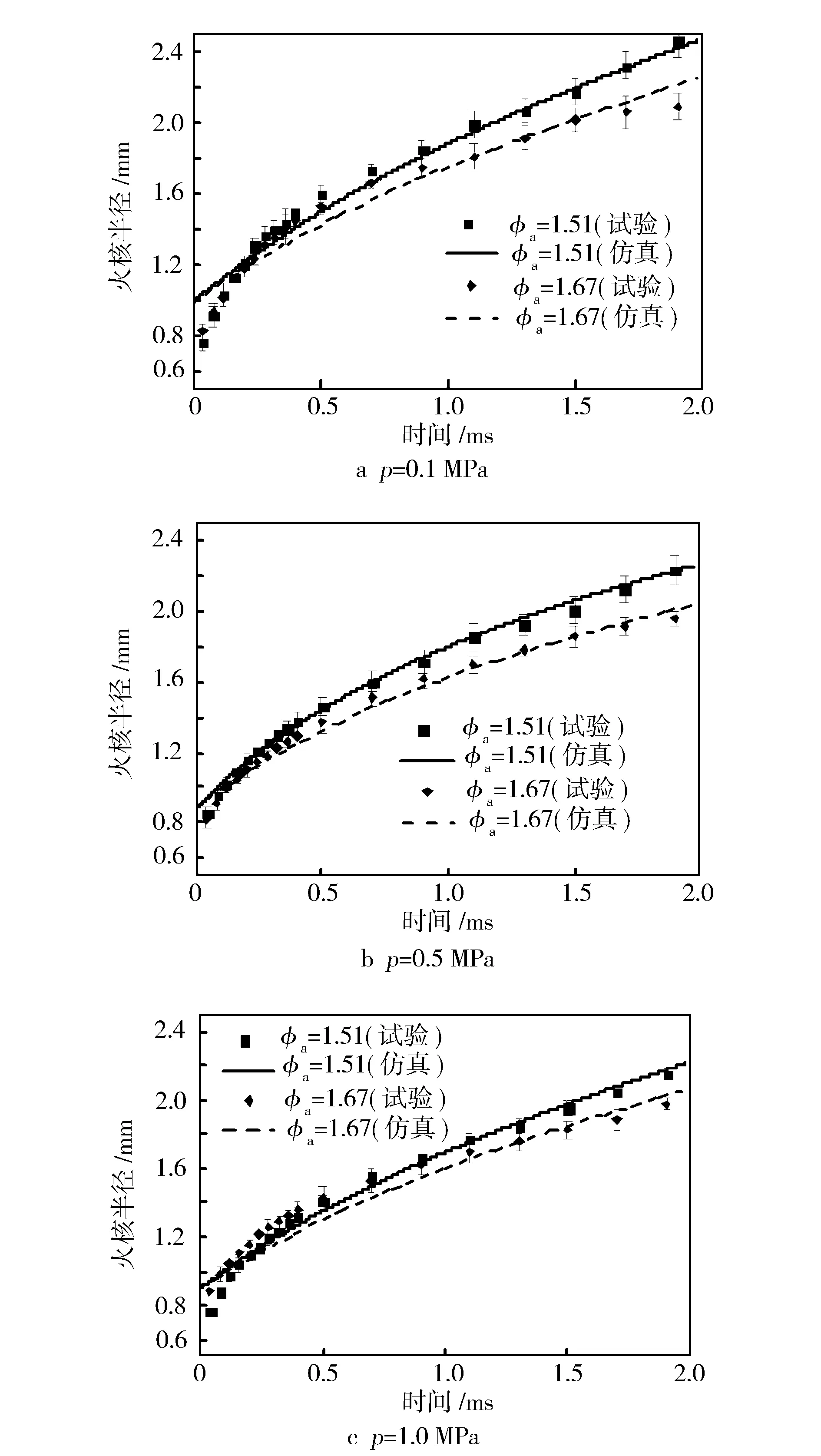
图6 过量空气系数对初期火核半径发展的影响

在仿真模型中，一方面未考虑等离子体通道热膨胀效应，忽略了弧光过程，另一方面根据击穿能量计算的火核初始半径略大于实际产生的火核初始半径，因此在0.5 ms之前与试验存在0.1～0.2 mm的差异。0.5 ms之后，仿真与试验结果趋于一致，在分析可燃混合气浓度以及点火能对初期火核的影响时忽略仿真前期误差。

如图6所示，同一压力下，混合气越稀薄，初期火核发展速度越缓慢。同一当量比下，初期火核在0.1 MPa时发展最快，压力越高，发展越缓慢，这是由于初始环境压力越高，层流燃烧速度越小。在高环境压力下，当量比对初期火核的影响相对较小。

3.3 点火能的影响

图7示出不同压力下分别采用单线圈与并联四线圈初期火核半径变化。由图7可知，增加点火线圈可以增加点火能量。试验中，采用的火花塞内阻为4.37 kΩ，将测得的放电电压减去由于火花塞内阻产生的电压，即可得到火花塞放电通道电压。将通道电压与电流值的乘积进行积分，计算出放电过程中由电路传递至混合气的能量。以1 MPa为例，单线圈击穿能量约为4.16 mJ，辉光过程次级线圈释放至混合气的能量约为55.70 mJ；而四线圈击穿能量约为13.19 mJ，辉光过程释放能量约为182.85 mJ。如图7所示，点火能的增加可有效地增加初期火核半径，在点火持续期(2 ms)结束时，火核半径可增加约10%。

由图7可见，不同压力不同点火能下，本模型均能很好地预测辉光期间初始火核半径的变化，可为研究不同点火策略对初期火核的影响提供支持。

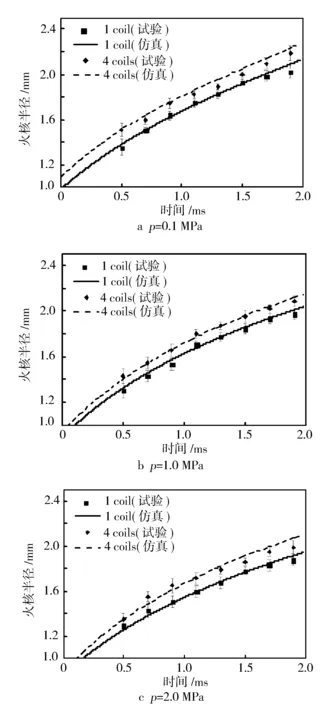
图7 并联线圈数对初期火核半径的影响

4 结论

a) 试验与仿真结果表明，在2 ms内，低压时初期火核发展较快，压力越高火核半径增加越慢；

b) 试验发现在点火初期，由于等离子体温度较高等原因，火核发展速度较快，之后逐渐变缓；仿真结果在点火初期与试验结果仍存在0.1～0.2 mm的误差，但是在点火后期火核半径发展与试验基本一致；

c) 在稀薄高压情况下初期火核发展缓慢，较难形成可自持发展的稳定火核，通过增加并联线圈的数量，可以提高放电过程中次级线圈电路电流，从而增加初期火核能量，促进初期火核发展；

d) 本研究发展的模型在不同压力与不同点火策略下，与试验结果较为吻合，可为后续研究不同点火策略对初期火核的影响提供支撑。

本一维拉格朗日模型可以较好地模拟静态条件下点火策略对初期火核发展的影响，但是尚存在局限性。后续研究中，应针对高压、复杂流场的情况下，点火通道形状延展及初期火核位置及形状变化，完整考虑击穿、弧光、辉光3个阶段，完善点火模型，以进一步探究高压高湍流稀薄点火机理。