巧用反比例函数“特定关系”解题分析

摘 要：函数是初中数学教学的重要课程，其教学特征是关注定量和数值之间的变化规律。函数知识在很多学科中都有应用，且初中数学注重讲解函数思想和方法，通过分析函数之间的特殊关系探讨教学中的问题。本文对初中数学中的“反比例函数”教学重难点和特定教学关系进行研究，希望能够为提升学生对反比例函数的认识，减轻其学习压力，提升教学质量绵尽微薄之力。

关键词：巧用;反比例函数;特定关系;解题分析

近年来，随着新课改的教学要求不断深入，中学数学教学对反比例函数的知识点要求更为严格，虽然在教学形式和内容上有了很大变化，但是学生在考试中要想获得高分依旧需要掌握基础知识点，只有了解基础，才有活学活用的可能。为了优创教学环境，提升教学质量，教师应当将反比例教学的重点落在基础教学和性质研究、内容钻研几个方面。

一、 研究初中反比例教学课程知识教学要求

新课改教学下，初中反比例函数教学要求学生掌握基础反比例函数特性，且在掌握反比例函数知识点基础上，可自主掌握相关延伸知识内容，以实现多题一解，一题多解的教学目标。本文针对八年级下册中的“反比例函数”这一章节进行研究，分析和研究教学设计中的反比例函数学习重难点，并不断探索教师对函数的教学理解过程，不断提升其学习质量，帮助学生了解反比例函数学习知识本质，养成积极、科学的逻辑思维能力，实现知识交流等目标，为提升数学综合教学奠定基础。

二、 分析反比例函数教学的难点和问题

（一）对基础概念掌握不明

反比例函数是很多数学习题的解决突破点，在很多和数值、图形相关的案例中，反比例函数都是可行、高效的求解方式。但是依旧存在很多学生“叫苦连天”，表示反比例函数应用难度大，学习难，可用性低。实际上，学生应用反比例函数来搭建图形，构建数、图关系时候，一定要了解图形和数字之间的关系。很多学生在看老师演练习题时候一看就懂，轮到自己做题时候却“山重水复疑无路”。实际上，这是学生对反比例函数概念认识不明，掌握不牢靠所导致。

反比例函数是坐标象限中不相交的双曲线，这两条曲线分布在正、负数值区域中，数值和图形的关系往往存在双面性。在学习中，学生为了尽快掌握知识点，死记硬背教师给的解题步骤，缺乏对自身掌握能力的分析。最终导致学生学习基础不稳固，随着后期知识点的深入，对教师所讲感到“云里雾里”。此外，还有很多教师在实际教学实践中，没有对学生进行相应的反比例函数概念讲解，直接让学生背公式，久而久之，学生对习题麻木，对概念淡漠化，认为反比例函数是两条不相交的曲线，其余深刻概念一概不知。

（二）机械化训练强度大，学生缺乏创新应用能力

反比例函數在初中数学内容中占据重要的地位，在实际的教学活动中，学生对函数教学知识的理解程度不高，为了赢得教师的认可、完成家人的目标、得到同学的关注，在学习中存在“邯郸学步”和“蹒跚学步”两种错误学习类型。急于求成学生掌握基础知识，得到教师夸奖后自信满满，开始钻研偏、怪题目，在特殊的习题中耗用大量时间，学习不均衡。另外一种学生对知识理解不深入，学习时候缺乏自信，总是死扣概念，重复练习简单习题，不愿意思考，突破自己，尝试中难度习题。

可见，教师对反比例教学感知敏感性不佳，学生重复性地学习、理解习题，缺乏一个思维跳板，最终塑造出过于自负、过于自卑两类学生。建议教师把握整体教学方向，为学生讲解反比例函数在中学数学教学的地位和重难点掌握程度，端正学生的学习心态和学习价值观，提升反比例函数教学的重要性。

三、 分析反比例函数的性质特征

中学数学教学中，数学教师可从基础概念突破，让学生理解反比例函数的教学特性，以此来加深学生对反比例函数的理解，实现数学性质、逻辑思维等多个方面突破。

（一）反比例函数的基础性质

反比例函数的图像属于以原点为对称中心的中心对称的两条曲线，反比例函数图像中每一象限的每一条曲线会无限接近x轴y轴但不会与坐标轴相交（y≠0）。

一般地，如果两个变量x、y之间的关系可以表示成y=k/x（k为常数，k≠0）的形式，那么称y是x的反比例函数。因为y=k/x是一个分式，所以自变量x的取值范围是x≠0。而y=k/x有时也被写成xy=k或y=k·x-1。k>0时，图像在一、三象限。k<0时，图像在二、四象限。k的绝对值表示的是x与y的坐标形成的矩形的面积。

（二）反比例函数的特殊性质和案例分析

1. 反比例函数的共生性研究分析

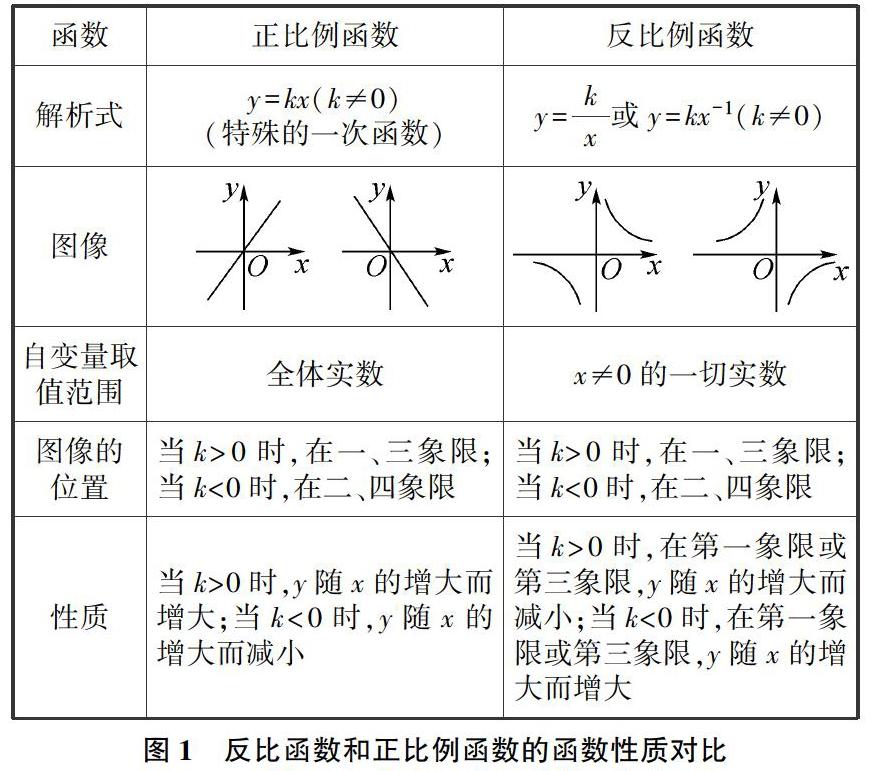
反比例函数编入初中课程教学时间不长，但其核心本质始终是函数，虽然涉及了数值、公式、图形坐标之间的关系，但依旧可以从分析函数的角度来研究反比例函数。反比例函数和函数的共生性有奇偶性、对称性、点调性。教师在为学生介绍反比例函数时候，可以将其对比其他函数例如正比例函数，以此来激发学生的好奇心，提升其判断力，提升其解题效率（如图1所示）。

函数正比例函数反比例函数

解析式y=kx（k≠0） （特殊的一次函数）y=kx或y=kx-1（k≠0）

图像

自变量取 值范围全体实数x≠0的一切实数

图像的 位置当k>0时，在一、三象限;当k<0时，在二、四象限当k>0时，在一、三象限;当k<0时，在二、四象限

性质当k>0时，y随x的增大而增大;当k<0时，y随x的增大而减小当k>0时，在第一象限或第三象限，y随x的增大而减小;当k<0时，在第一象限或第三象限，y随x的增大而增大

图1 反比函数和正比例函数的函数性质对比

2. 反比例函数的特殊性

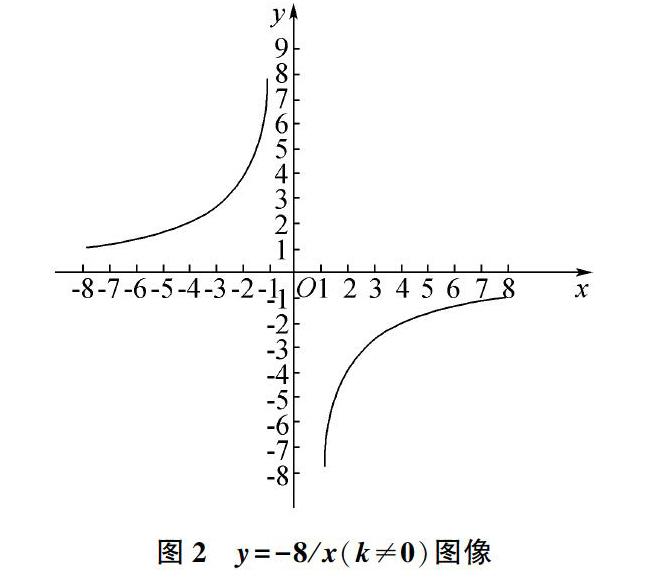
反比例函数对比其他函数，其具备独特的应用价值和使用性质，这也让其在众多的函数环境中得以突破，彰显价值。很多学生表示，在解题中难以将反比例函数和学习习题联系起来，缺乏解题思路。对此，建议教师从反比例函数的特有性质进行突破。首先，绘画图形，反比例函数的图像和其他函数图像不同，教师可以利用图像关系来引导学生理解、认识反比例函数性质，并采用数形结合的方式完成学习任务。经过图形的对比，学生可以观察得到不同性质的函数图像关系，进而加深对抽象性质的认识。如下案例所示（如2所示）。观察函数y=k/x（k≠0）的特殊图像，分析其线条走势和数字关系;当k值为-8时，图像如下图2所示。

图2 y=-8/x（k≠0）图像

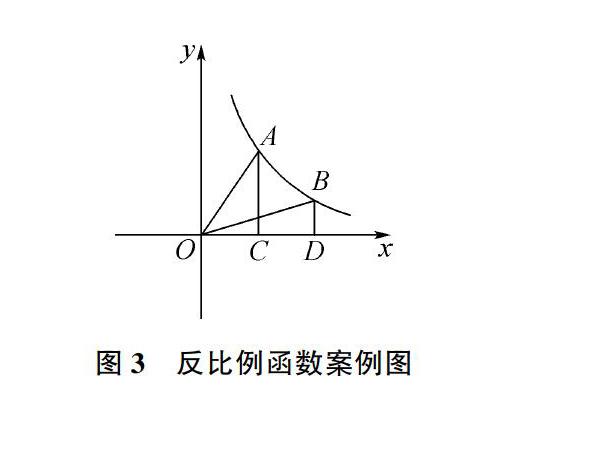
根据其图像特征，现解题y=1/x（x>0）的不同坐标点和原点组成的三角形图像关系面积。例如下图3所示。

图3 反比例函数案例图

研究函数该类型问题要透视函数的本质特征。反比例函数中，比例系数k有一个很重要的几何意义，那就是：过反比例函数图象上任一点P作x轴、y轴的垂线PM、PN，垂足为M、N则矩形PMON的面积为。所以，对双曲线上任意一点作x轴、y轴的垂线，它们与x轴、y轴所围成的矩形面积为常数。这个常数是k的绝对值。在解有关反比例函数的问题时，若能灵活运用反比例函数中k的几何意义，会给解题带来很多方便。此题可以从反比例函数定义，所有的类似图像上围成的三角形面积都应该是相等的;其次，可采用取点计算面积对比可知，实际上，上图△AOC和△BOD的面积经过假设值带入计算，其中A（1，1）;B（2，0.5）和原点围成的三角形经过计算面积也是相等的。

3. 反比例函数的应用性价值

反比例函数是中学数理化习题中常用的技巧。例如物理课程中的速率计算等，這些知识关系到了初中中学学生的多学科发展，对学生的学习成长有重要的价值意义。在学习中，教师要注意学生的反比例函数的实际应用，要引导学生积极掌握知识点重点内容，不断提炼函数的知识点，最终将其运用到多学科，生活中去。如下图4教学案例可知。

假设A/B两地的距离为S，求解以汽车从A到B匀速运动，此时汽油消耗量为x升每小时，需要学生求出两地运输距离的总耗油量y升和汽车行驶速度v关系是怎样的。首先，学生要了解耗油量和速度之间的关系，其中行驶时间为h=S/v，耗油量是y=S/v*x，且所有的计算值都应该是正值。经过整合计算后可为y=S*x/v。答案如下图4所示。

图4 反比例函数例题答案

四、 结语

综上所述，反比例函数和传统的数学教学方式不一样，且图形教学知识点并不是连贯的，教师在教学中要注意引导学生对知识点性质的理解，关注反比例函数和其他函数之间的相关性，探讨和图像之间的关系，不断锻炼学生对知识点的掌握、理解能力，引导学生将知识推广应用与生活，最终提升数学教学的质量。

参考文献：

[1]史纪鑫.课堂因生成而精彩：国培计划（2019）甘肃省项目县级教师培训团队研修项目第二阶段心得体会[J].教育革新，2019（12）：9-10.

[2]杨金洪.初中数学反比例函数的研究[J].中学课程资源，2020（2）：66-68+33.

作者简介：

谢建宝，福建省龙岩市，福建省龙岩市上杭县第三中学。