零膨胀Poisson回归模型极大似然估计的相合性与渐近正态性
侯 文, 蔡梦瑶, 谢新惠
(辽宁师范大学 数学学院,辽宁 大连 116029)
Poisson回归模型通常用于计数数据的统计分析,应用十分广泛. 但是,在实际问题的研究中,当出现零观测值过多的情形时,Poisson回归模型已不再适用了.针对此种情况,Lamber[1]提出了零膨胀Poisson回归模型,并且用该模型对生产过程中产品所含有的瑕疵数量进行了分析. 关于零膨胀Possion回归模型研究的文献很多,例如,Welsh等[2]采用零膨胀Poisson回归模型分析了珍稀物种的生存状况, Shankar,Milton和Mannering[3]把该模型用于对事故发生频数的建模.还有Bohning等[4]分析了有关牙科流行病预防研究中的数据,Cheung[5]分析了医学调查中关于儿童生长发育的数据,都用了零膨胀Poisson回归模型. 目前文献大多是从实际问题出发,主要注重于模型的应用,而涉及零膨胀Poisson回归模型极大似然估计的相合性和渐近正态性等大样本性质的研究文献并不多见.本文借鉴Fahrmeir和Kaufmann[6]对广义线性模型极大似然估计大样本性质的研究结果,在一定的正则条件下,证明了零膨胀Poisson回归模型极大似然估计的相合性和渐近正态性等性质.
1 零膨胀Poisson回归模型介绍
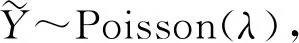
如果随机变量Y服从零膨胀Poisson分布,λ、ω为参数,其概率分布律为
记作Y~ZIP(λ,ω),则其均值和方差分别为
E(Y)=(1-ω)λ,
Var(Y)=E(Y)(1+λω)=(1-ω)λ(1+λω).
零膨胀Poisson回归模型与广义线性模型的构成类似,模型结构如下:
(i)模型的响应变量为Yi,Yi~ZIP(λi,ω),且Yi相互独立,i=1,2,…,n.
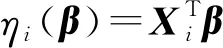
(iii)线性组合ηi(β)与Yi的均值λi之间有指数型函数联结,即λi=exp(ηi(β)),i=1,2,…,n.
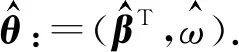
令
ZIP回归模型的对数似然函数为
(log(1-ω)-log(yi!)+yilog(λi(β))-λi(β)).
其Score向量
sn(θ)=(s0(θ),s1(θ),…,sp(θ),sp+1(θ))T.
其中,
又
xirI{yi>0}(yi-λi(β)),
而
2 条件和引理
在给出假设条件之前,先设定一些记号. 令λminA和λmaxA分别表示方阵A的最小特征根和最大特征根;用AT表示矩阵A的转置矩阵;A1/2表示正定矩阵A的Cholesky分解中左平方根的下三角矩阵,且其对角元素为正,即A1/2(A1/2)T=A.为表示方便,设定AT/2∶=(A1/2)T,A-T/2∶=(AT/2)-1,A-1/2∶=(A1/2)-1.

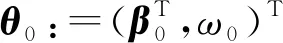
Hn(θ)和Fn(θ)分别表示为ZIP回归模型参数θ的观测信息阵和Fisher信息阵.
此外,为了记号的简便,分别将λi(β0)、sn(θ0)、Fn(θ0)、Eθ0和Pθ0记为λi、sn、Fn、E和P.
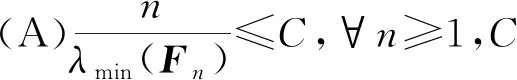
(B){Xn,n≥1}⊂Kx,Kx⊂p+1是一个紧集;
(C)假设B⊂p+1是一个开集且θ0是集合Kθ∶=B×Ω的内点,其中,Ω:=[0,1];
零膨胀Poisson回归模型的观测值矩阵为
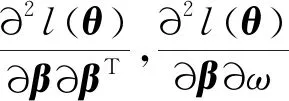
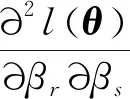
(1)
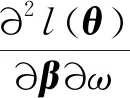
Fisher信息阵Fn(θ):=EθHn(θ),有
fr,s(θ)=fs,r(θ)=
(2)
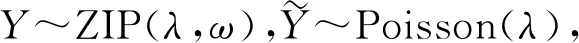
若函数u(·)在[0,∞)是非负的,有
高职院校要与校外酒店合作,为学生酒店英语的实际应用搭建一个平台,实现教室—模拟—酒店三位一体的教学环境,将把酒店中的工作和交流与酒店英语结合起来,培养学生综合素质,实现酒店行业的复合型人才战略。通过学生与学生之间,学生与老师之间的相互教与学,实现生动有趣、多种多样的教学方式,逐步提高学生的酒店英语应用能力。
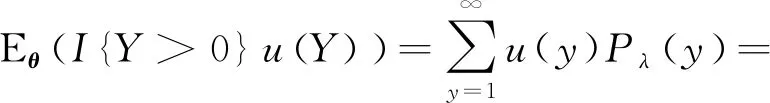
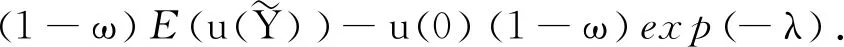
由函数u(·)在[0,∞)是非负的,显然有
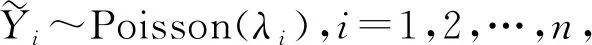
其中,k为整数,k>0,C1>0,且C1取决于k,θ0.
证根据Gupta[7]中定理1,有递推公式
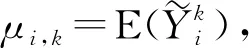
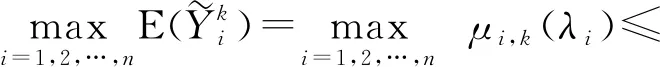
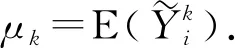
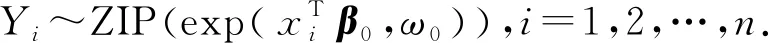
其中,C>0且取决于k,θ0.
证在假设(A)下,对∀n∈,邻域Nn(ε)是紧集,且对于∀ε>0,当n→∞时,Nn(ε)收缩于θ0.因此由引理2.1和引理2.2以及多项式Qk(y)系数的连续性,有
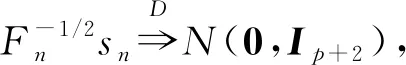
证由Gramer-Wald策略,对∀a∈p+2(a≠0),且使得令由于因此,可由Lyapunov条件
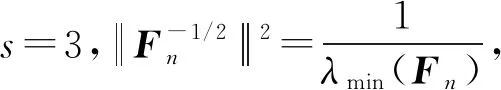
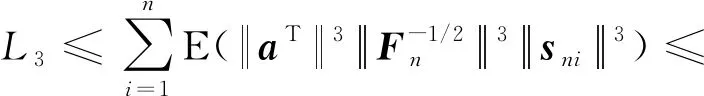
由Cr不等式
(3)
有
由式(3)得
4Ap(θ0)+4Bp(θ0).

再由Cauchy-Schwarz不等式和引理2.2,得

其中,Y~Poisson(exp(xTβ0)),Yi~Poisson(λi),i=1,2,…,n.
引理2.5在假设(A)~(C)下,有
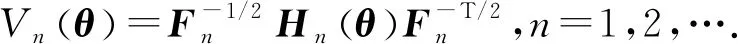

即只需证明
(4)
(5)
为了证明式(4),需证明
(6)
(7)
(8)
由于式(6)~式(8)有相似的结构,只证明式(6)成立,其他可类似处理.
令
urs(θ)∶=xirxis(1-ω)λi(β)(exp(-λi(β)))×
vrs(θ)∶=xirxisλi(β).
为得到式(6),只需证
(9)
(10)
由大数定律可得,式(9)、式(10)成立.
下面看式(5),有
(11)
(12)
(13)
由于式(11)~式(13)有相似的结构,只证明式(11)成立,其余可用类似处理.
当n充分大时,由θ∈Nn(ε),由式(2)中frs(θ)的连续性,可得式(11)成立.
3 主要结果

证令∂Nn(ε)表示Nn(ε)的边界,由假设(A)知,当n→∞ 时,Nn(ε)收缩于θ0.
则
ln(θ)-ln(θ0)<0,∀θ∈∂Nn(ε).
(14)
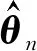
有
P(ln(θ)-ln(θ0)<0, 对∀θ∈∂Nn(ε))≥1-η
(15)
成立.由此可以推得定理3.1的(i)和(ii)成立.
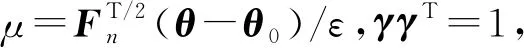
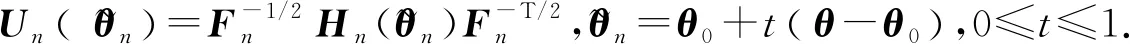
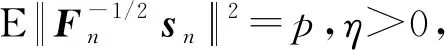
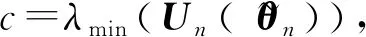
由此可知式(15)成立.
由引理2.4和引理2.5即可推得定理3.1的(iii)成立.

