一种磁性材料剩余损耗统计参数的高效提取方法

宋金薇， 李 琳， 刘 任

(华北电力大学 新能源电力系统国家重点实验室，北京 102206)

0 引 言

全球对于电力能源需求及质量要求日益增加，磁性材料在电力设备和电力器件中的应用也日益广泛，准确预测磁性材料的损耗在理论和实践中仍然是一个很重要且被广泛关注的问题，对于电力电子设备和器件的设计和最佳化选择也有着至关重要的意义。

因为损耗统计理论简单实用，20世纪90年代开始广泛用于磁性材料损耗的工程计算[1,2]。损耗统计理论将磁性材料的总损耗分为三部分：磁滞损耗Phy,涡流损耗Peddy，剩余损耗Pex。计算三个分量都需要确定一些与材料有关的参数：确定磁滞损耗时，需要测量静态铁损(即频率趋近0 Hz下的损耗)，与频率无关，故称为静态损耗；涡流损耗和剩余损耗与频率有关，被称为动态损耗。对于涡流损耗，在低频时，集肤效应不明显，可以被忽略，这时只需要根据Maxwell方程，利用测得的材料的厚度与电导率计算即可得到涡流损耗；无取向硅钢片具有小的晶粒尺寸和空间随机的磁畴结构[3-5]，其剩余损耗很小，一般可以忽略，而对于应用于大型变压器、电抗器等电力设备的有取向硅钢片，剩余损耗分量则不能忽略。因此能否准确计算剩余损耗，决定了能否准确预测磁性材料在各种工况下的损耗[1，6，7]。传统斜率法提取剩余损耗统计参数来预测剩余损耗时，理论上只需两个频点的实验结果就可提取出剩余损耗统计参数，从而得到剩余损耗，但此种方法的准确性依赖于选取的两个频点的实验数据，难以保证宽频带下的准确度。如果要提高准确性，就需要处理很多频点下的实验数据，非常不方便。

为此，本文结合损耗统计理论和磁粘度型动态磁滞模型，提出一种高效提取损耗统计理论剩余损耗统计参数的方法，对于研究磁性材料的剩余损耗统计参数具有重要的意义。另外，磁滞模型的选择对于损耗预测的准确性也很重要，因为Preisach模型有着坚实的物理基础且能准确地模拟磁性材料的磁滞特性，而且相关理论已经发展地相对成熟，故本文选择动态Preisach模型(Dynamic Preisach Model)[8]模拟磁性材料的磁特性，以验证本文所提方法的准确性。

1 损耗统计理论及其剩余损耗统计参数提取方法

1.1 损耗统计理论

Bertotti提出的损耗统计理论从磁性材料内部微观磁化机理出发，研究了磁畴及磁畴壁的运动情况，根据损耗产生原因的不同，将总损耗分解为磁滞损耗Why,涡流损耗Weddy和剩余损耗Wex，并且已经取得了广大学者的认可[9,10]。根据损耗统计理论，磁性材料的总损耗为

W=Why+Weddy+Wex

(1)

式中：磁滞损耗Why为静态磁滞回线(频率为0时)的面积，它与频率无关[11]；涡流损耗Wcl又名经典涡流损耗。假设磁性材料被均匀磁化，产生均匀分布的感应电流，这种感应电流变化产生与频率f成比例变化的涡流损耗Wcl，对于厚度为d，电导率为σ的磁性材料，其涡流损耗大小为

(2)

剩余损耗Wex为实验测得的总损耗减去以上两个损耗分量得到的差值，它与材料的微观结构如晶粒、磁畴及磁畴壁等以及磁畴壁的运动规律有关。 Bertotti推导出剩余损耗的解析表达式为

(3)

式中：σ为磁性材料的电导率；S为磁性材料横截面积；G为无量纲系数(G=0.137 5)；V0为表征局部磁场分布的统计参数。

1.2 传统剩余损耗统计参数的提取方法

当正弦激励下交流磁通密度峰值为Bp时，式(3)的剩余损耗可等效为式(4)[12]:

(4)

由于磁滞损耗与频率无关，由式(4)可知，在相同磁通密度峰值下，总损耗与涡流损耗之差(W-Wcl)与频率的平方根(f0.5)呈线性关系[12]。因此，该线性函数与纵坐标轴的交点即为磁滞损耗值。斜率k=8.76(σSGV0)0.5Bp1.5，因此，可以根据斜率k计算出剩余损失的统计参数V0。

当磁通密度峰值Bp不同时，计算结果和实验数据中提取的线性回归函数分别表示的总损耗和涡流损耗之差(W-Wcl)与频率的平方根(f0.5)之间的关系如图1所示。

根据以上理论，只要实验测得两组不同频率下的总损耗和涡流损耗，即可得到上文的斜率k，从而得到剩余损耗参数V0。该方法计算损耗的准确性依赖于采用的实验测得数据的两个频点的损耗，对于宽频损耗特性，需要采用大量的实验数据，一一算得剩余损耗统计参数V0值，既不方便也不快捷。因此本文提出一种更高效的剩余损耗统计参数V0的提取方法，不需要大量的实验数据就能高效地提取剩余损耗参数V0，而且相比传统的斜率法提取剩余损耗统计参数，误差更小。

2 剩余损耗统计参数高效提取方法

在测量动态磁损耗的实验中观察到磁感应强度B存在落后于磁场H的时间滞差，这种时间滞差被定义为磁粘度[13]。文献[14]用上个世纪提出的一些物理模型和半经验模型对此做出了解释，这些物理模型和半经验模型基于Bertotti提出的动态Preisach模型(Dynamic Preisach Model)[8]，将磁粘度归因于Preisach磁偶极子的惯性，这种磁粘度型动态效应(viscous-type model)表示为

(5)

式中：ν为动态模型因子，可以表示其与频率的比例关系；r(B)定义为动态磁阻率[15]，为磁感应强度B的函数或者为常数，H0为静态磁滞场。在很多实验中发现动态磁阻率r(B)在磁感应强度B=0附近时达到最大值，在磁感应强度B接近正的或者负的饱和值时最小，其表达式为

r(B)=R0[1-(B/BS)2]

(6)

式中：R0为与材料有关的常数，可由实验测量数据确定；BS为饱和磁感应强度。

求解方程(5)可得

(7)

剩余损耗的本质为磁滞特性而非涡流损耗，施加场H与磁滞场H0的数值差即为剩余场大小，因此式(7)的第二项即为剩余场大小：

(8)

式中：δ为关于dB/dt的符号函数，当dB/dt为正数时，δ为1；当dB/dt为负数时，δ为-1；从式(8)可以看出剩余场大小与|dB/dt|1/ν成比例，而基于损耗统计理论的动态Preisach模型中剩余场大小与f0.5成比例，故此处ν的值为2。

根据损耗统计理论剩余损耗表达式(3)，剩余损耗Wex在极短时间dt内的微小增量dWex可以表示为

(9)

又因为对于Hex有以下等价关系：

(10)

故根据(9)和(10)可推得

(11)

式中：λ为关于dB/dt的符号函数，当dB/dt为正数时，λ为1；当dB/dt为负数时，λ为-1。

根据式(8)和式(11)，本文推导出损耗统计理论剩余损耗统计参数V0的表达式为

(12)

3 实验验证

为了验证本文高效提取方法的准确性，采用BROCKHAUS-MPG200电工钢系统测量了不同正弦激励下硅钢片样本的磁滞回线。BROCKHAUS-MPG200电工钢系统用于电工钢的磁特性测量，可根据测量需求选择不同的测量单元；同时采用采用全数字化的数据采集系统，可实现磁场强度H与磁感应强度B的并行存储，从而保证H和B的同步测量，进而避免由相位差而产生的测量误差；其次，为保证磁滞回线等磁特性数据测量的准确性，该系统采用自适应负反馈算法，自动调节激励电源的输出电压。因此，该系统的测量方法及结果符合国际电工委员会标准“IEC60404-2”[16]。H(t)、B(t)大小分别由式(13)和(14)计算求得，实验测量平台如图2所示。

(13)

(14)

式中：N是线圈的匝数；i1初级线圈的励磁电流；lm为等效磁路长度；A为磁环的等效横截面积；u2是次级线圈两端之间的电压。

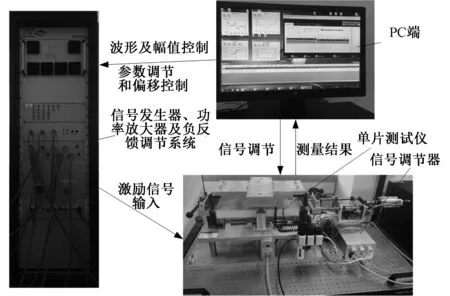
图2 BROCKHAUS-MPG200电工钢测量系统Fig.2 BROCKHAUS-MPG200 electrical steel measuring system

本文选取的硅钢片试样为26Q94(长方体)，其参数如表1所示。同时图3验证了本文模拟静态Preisach磁滞模型的准确性。

表1 硅钢片样品26Q94的参数

Tab.1 Parameters of silicon steel sheet sample 26Q94

参数样品26Q94长度/mm300宽度/mm30厚度/mm0.259 4横截面积/m24.668 845 316×10-5电导率/(S/m)2.27×106密度/(kg/m2)7 650

基于本文提出的剩余损耗统计参数V0的高效提取方法，图4对比了频率为50 Hz时正弦激励下V0随磁密Bp的变化趋势, 同时仿真了硅钢片样品26Q94在频率分别为50 Hz、100 Hz、150 Hz、200 Hz、250 Hz和300 Hz下的动态磁滞回线，并和传统斜率提取法得到的动态磁滞回线(选取两个频点提取出剩余损耗参数V0以计算动态Preisach模型的损耗)进行了对比，结果如图5～13所示。从图5～10中可以看出，相比斜率提取法，本文高效提取法的计算结果和实验结果更为接近。由图11可以看出，基于损耗统计理论，通过斜率提取法和本文提出的高效提取法得到的动态损耗相比实验测量损耗都呈现一定的误差，斜率提取法的动态损耗误差随磁密增大呈现减小的趋势，而高效提取法的动态损耗误差随磁密的增大呈现先减小后增大的趋势，尤其当磁密接近饱和磁密时，其误差增大很快，但整体误差仍小于斜率提取法得到的动态损耗误差。由图11、12可以看出，两种方法在频率超过200 Hz后，其动态损耗误差都逐渐增加，尤其频率超过250 Hz之后，两种方法算得的动态损耗误差都将不可接受(图9～10所示)，原因在于随着频率增大，集肤效应增强，Berttoti推导的涡流损耗解析公式(如文中公式(2)所示)假设了磁场沿磁性材料内部均匀分布，因而当样品在高频段出现集肤效应时，该损耗统计理论及公式不再适用。总之，斜率提取法计算的动态损耗的准确性依赖于采用的两个频点下测得数据的准确程度，为提高准确性，不得不采用大量的实验数据，一一算得剩余损耗统计参数V0值，既不方便，也不快捷，而本文提出的高效提取法通过结合损耗统计理论与一种磁粘度型动态模型直接推导出损耗统计理论剩余损耗统计参数的解析表达式，且计算结果误差较小，相比斜率提取法节省了大量的时间。

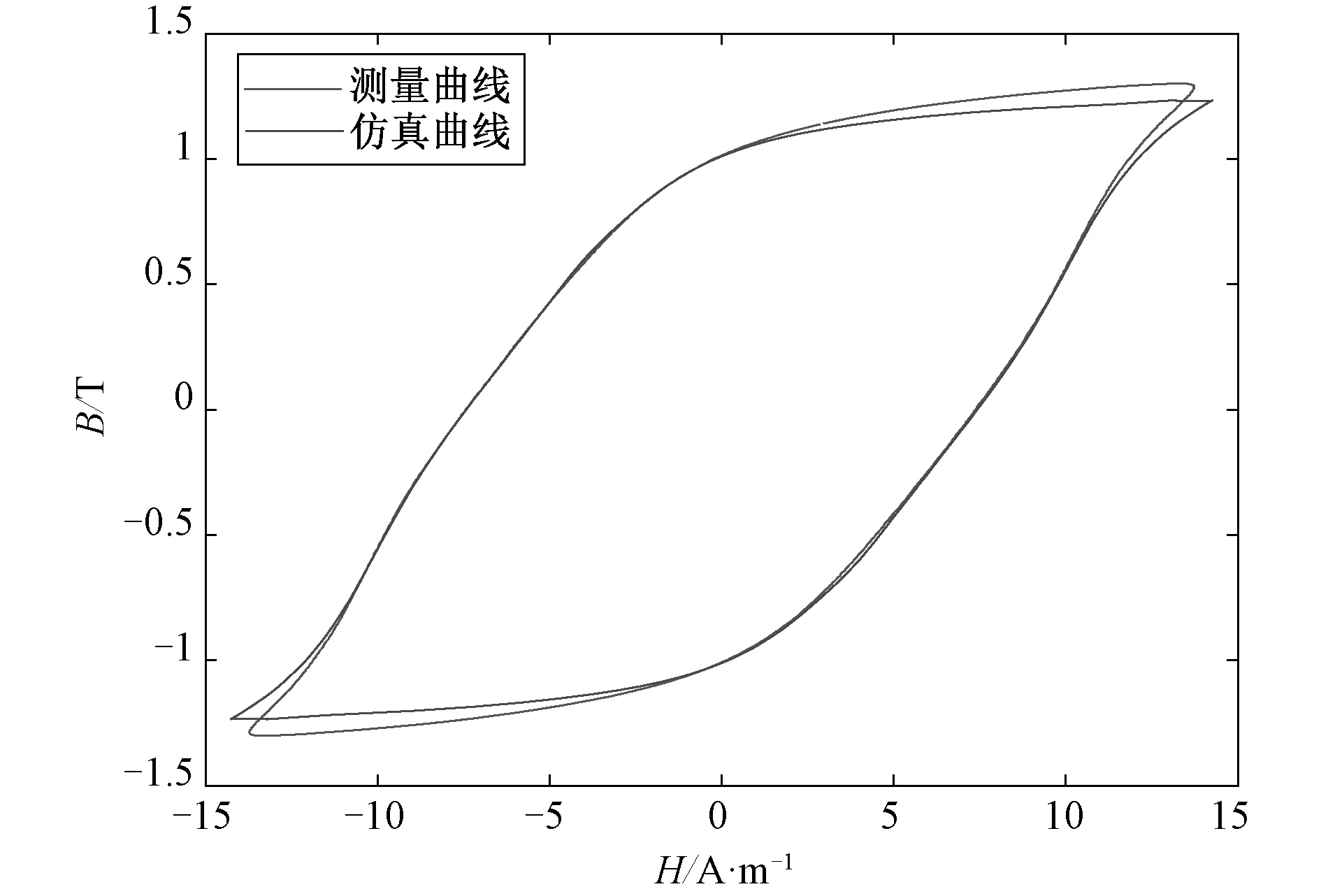
图3 静态仿真磁滞回线与实测磁滞回线对比Fig.3 Comparison of simulated static hysteresis loop with measured static hysteresis loop

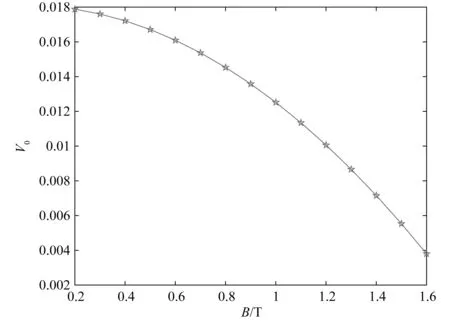
图4 高效提取方法提取剩余损耗统计参数V0随磁密变化关系Fig.4 Relationship between excess loss parameter V0 and magnetic density calculated by efficient extraction method

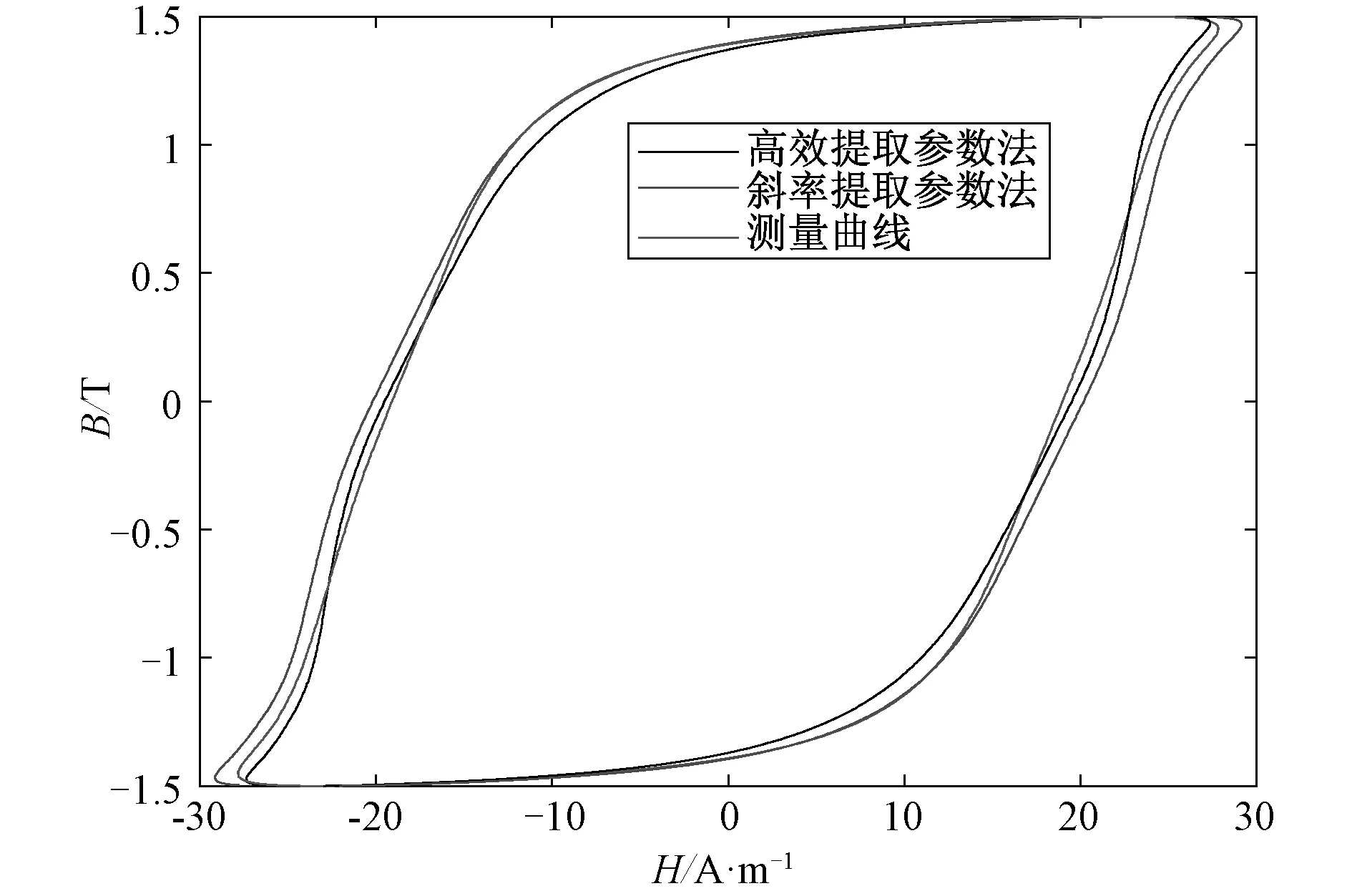
图5 样品在 f=50 Hz下的动态磁滞回线Fig.5 Dynamic hysteresis loop of the sample at f=50 Hz

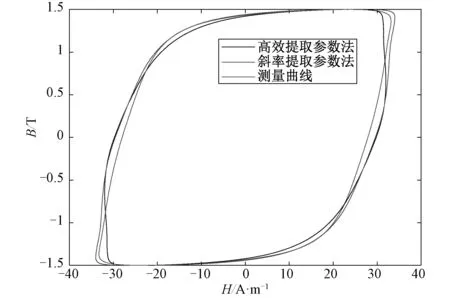
图6 样品在f=100 Hz下的动态磁滞回线Fig.6 Dynamic hysteresis loop of the sample at f=100 Hz

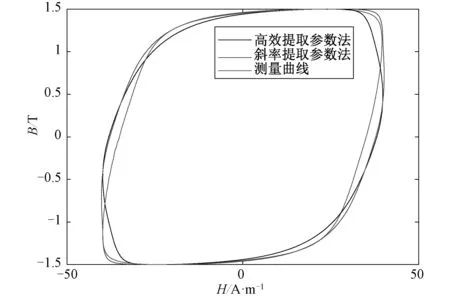
图7 样品在f=150 Hz下的动态磁滞回线Fig.7 Dynamic hysteresis loop of the sample at f=150 Hz

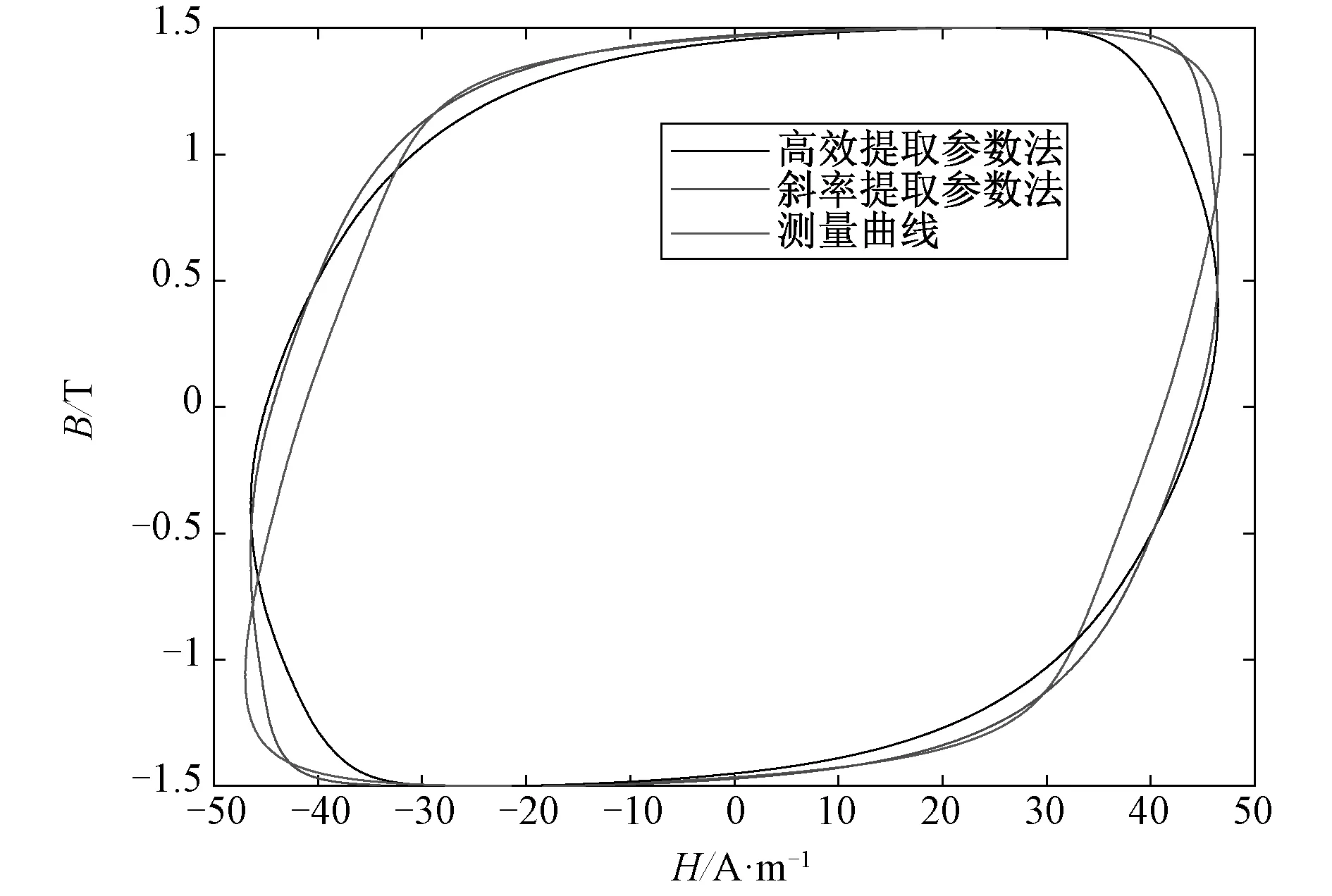
图8 样品在f=200 Hz下的动态磁滞回线Fig.8 Dynamic hysteresis loop of the sample at f=200 Hz

图9 样品在f=250 Hz下的动态磁滞回线Fig.9 Dynamic hysteresis loop of the sample at f=250 Hz

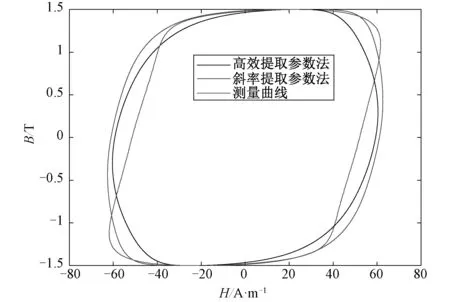
图10 样品在f=300 Hz下的动态磁滞回线Fig.10 Dynamic hysteresis loop of the sample at f=300

图11 斜率提取参数法与高效提取参数法预测损耗的误差随磁密变化对比(f=50 Hz)Fig.11 Comparison of loss prediction error varying with magnetic density between slope extraction method and efficient extraction method (f=50 Hz)

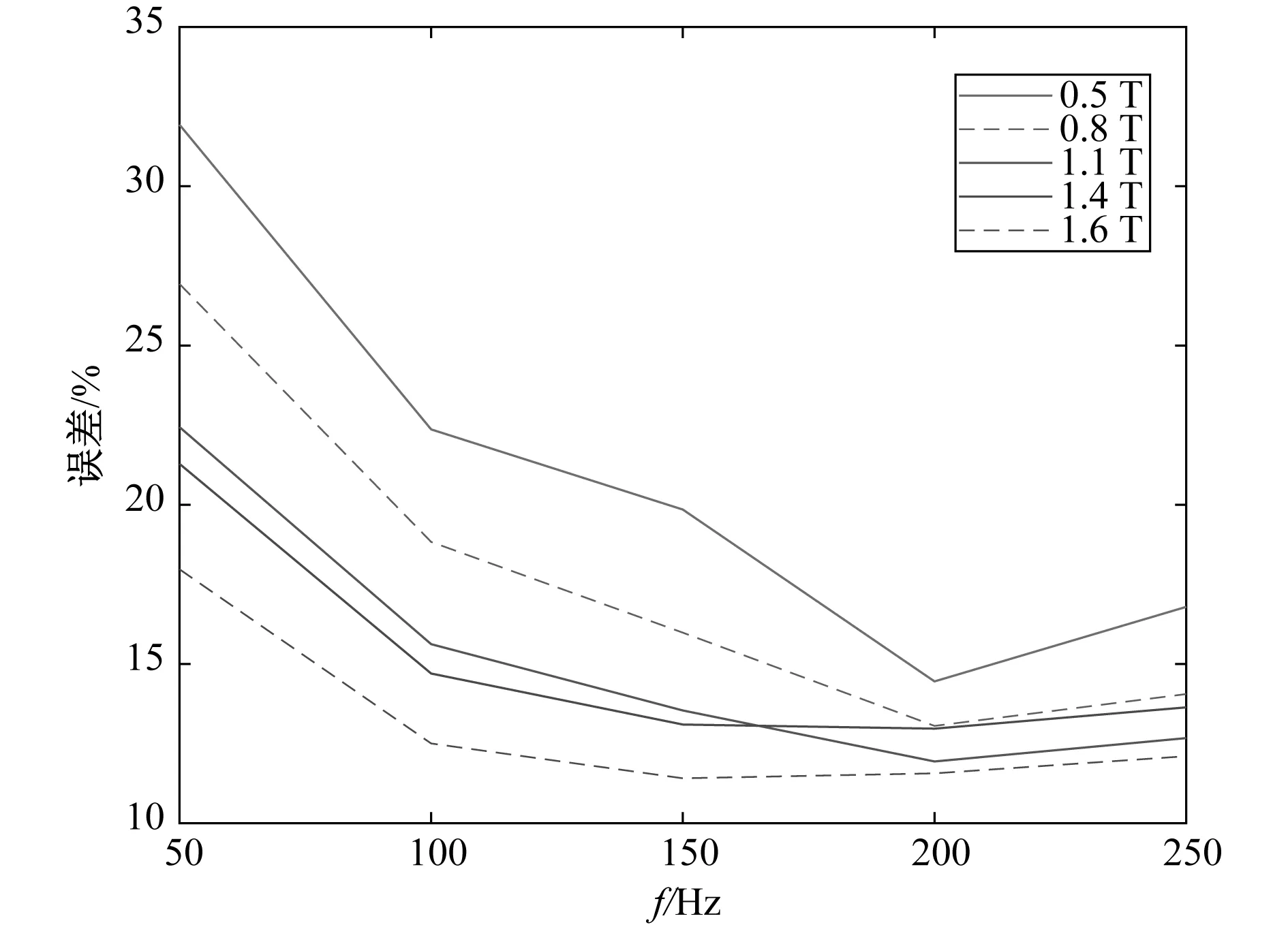
图12 斜率提取参数法在不同频率下预测损耗的误差随频率变化对比Fig.12 Comparison of loss prediction errors at different frequencies using slope extraction method

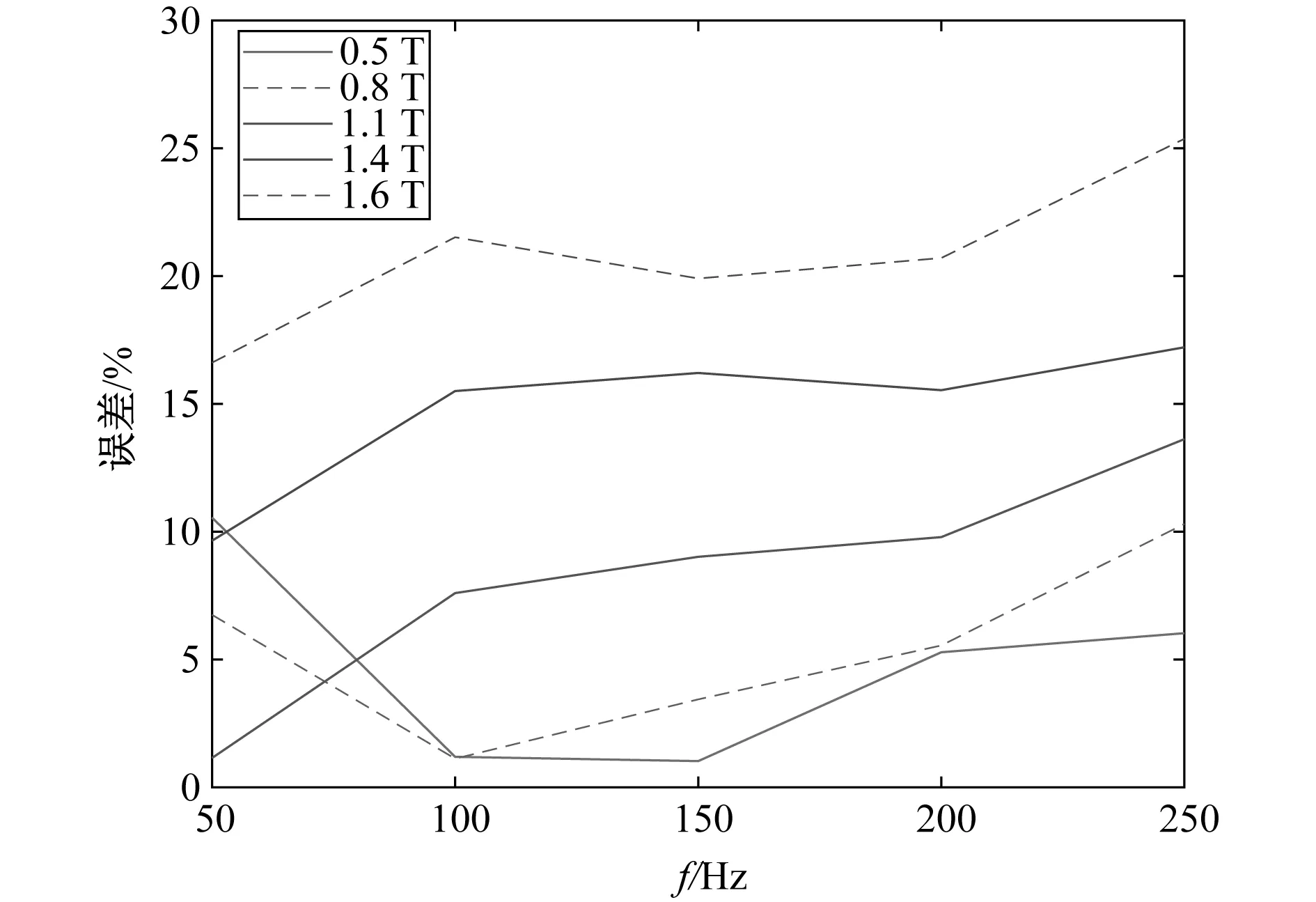
图13 高效提取参数法在不同频率下预测损耗的误差随频率变化对比Fig.13 Comparison of loss prediction errors at different frequencies using efficient extraction method

此外，本文还计算了样品在不同频点下的损耗值，同时和斜率法(选取两个频点提取出剩余损耗参数V0以计算动态损耗)的计算结果、测量结果进行对比，如表2所示。从表中可以看出，相比于传统剩余损耗统计参数V0提取的斜率法，本文所提方法不仅精度更高，且计算效率也更高(斜率法需要对两个频点下的实测数据进行处理，运用所得图像的斜率得到所需提取的剩余统计参数V0，因而提取程序较为繁琐；而本文所提方法直接利用推导的公式(12)即可得到剩余损耗统计参数V0)。

表2 两种方法计算损耗与测量损耗对比(Bp=1T)

Tab.2 Comparison of calculated losses by two methods with measured losses (Bp=1T)

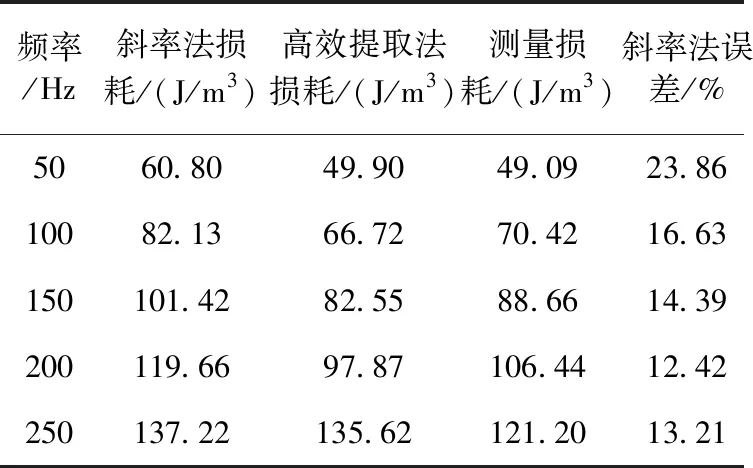
频率/Hz斜率法损耗/(J/m3)高效提取法损耗/(J/m3)测量损耗/(J/m3)斜率法误差/%高效提取法误差/%5060.8049.9049.0923.861.6610082.1366.7270.4216.63-5.25150101.4282.5588.6614.39-6.89200119.6697.87106.4412.428.06250137.22135.62121.2013.2111.89

4 结 论

(1)本文结合一种磁粘度型动态模型，推导出该动态模型剩余损耗对应场强度分量的解析表达式，再基于损耗统计理论，推导出剩余损耗相应场强度分量的解析表达式，最后结合两者推导得到损耗统计理论剩余损耗统计参数的解析表达式，并利用实验结果验证了本文高效提取方法的准确性和实用性。

(2)由于Berttoti在基于损耗统计理论推导涡流损耗计算式时，假设了磁性材料内部的磁场是均匀分布的，因而其不适用于使样品出现集肤效应的高频频段，因此本文方法仅适用于正弦激励下硅钢材料低频动态损耗的计算。故课题组拟转换基于损耗统计理论的动态损耗计算思路，尝试将已适用于铁电材料宽频动态磁滞、损耗特性的分数阶导数引入静态Preisach模型，准确、高效地实现磁性材料动态磁滞行为的宽频建模。