基于PMU同步测量的分区惯量估计方法

刘方蕾， 毕天姝， 闫家铭， 王 凡， 胥国毅

(华北电力大学 新能源电力系统国家重点实验室， 北京 102206)

0 引 言

随着新能源发电技术的发展，电力系统中新能源发电占比不断提高[1]。新能源发电系统通过电力电子换流器接入系统，其功率输出与电网频率动态解耦，无法像传统同步发电机一样，为系统提供惯量支撑和频率控制。随着电网中新能源占比的提高，电网的惯性时间常数下降，维持系统频率稳定的能力降低，另一方面，由于特高压交直流输电工程的大量投运，系统输送功率巨大，遭受大功率扰动的风险增大，系统频率稳定风险加大。评估系统惯量，对于研究系统的频率动态特性、指导新能源并网、研究电网频率稳定控制措施具有重要意义[2]。

系统的惯量水平通常用惯性时间常数来表示，表征了系统在出现功率不平衡时抑制频率变化的能力[3]，电网出现有功缺额后频率初始下降速度、频率最低点和最低点发生时间等重要指标均与系统惯性时间常数H密切相关。目前，对于系统惯量的评估主要有以下几种方法：基于小扰动估计方法、大扰动估计方法和基于稳态的估计方法。小扰动估计方法主要通过建立系统小信号模型，分析振荡特征等与系统惯量的关系，通过对振荡频率的测量来求取惯量常数[4,5]，这种方法适用于阻尼性能良好的系统，且对信号的处理技术要求较高,易受噪声影响，造成评估结果不准确。大扰动分析方法主要基于经典的发电机和转子运动方程，通过扰动发生后系统的功率不平衡量和系统频率变化率来计算系统惯量。随着PMU在电网中的大量装备，为准确测量系统中这些电气量提供了基础[6,7]。文献[8]通过最小二乘法对故障后的系统频率曲线进行5阶拟合，取一次项参数作为系统频率变化率，再根据测得的系统功率不平衡量求取系统惯性时间常数。文献[9]采用英国电网几次大扰动故障下PMU实测频率数据和功率不平衡量数据对电网的惯量进行估计，要准确评估系统惯量，需要已知功率缺额的大小。稳态估计方法主要是采用对机组惯量进行加权并结合各种机器学习方法进行评估，通过对大量历史数据的学习，建立系统稳态运行情况下，平均频率变化与系统惯量的关系，从而对实时运行的系统状态评估其对应的惯性时间常数[10,11]，对系统的惯量评估具有很高的精度，但这些机器学习方法通常只能计及机组提供的惯量，没有考虑负荷对系统的惯量贡献。系统中有大量感应电机负荷，文献[12-14]指出，故障后，不仅系统中的同步发电机组对惯量有贡献，负荷等也成为影响系统惯量响应的重要因素。

针对以上方法的不足，本文提出了一种基于PMU同步测量的分区惯量估计方法。这种方法利用扰动发生后PMU测得的各区域间联络线上功率的变化和系统频率变化，可分别计算出各区域的惯性时间常数，对系统的惯量水平有一个更为具体细致的描述，评估结果不仅仅包括发电机对于惯量的贡献，还考虑了具有惯量响应的负荷因素的影响。本文提出的估计方法，采用一种差值法进行计算，计算过程中不需要已知功率缺额的大小，解决了实际测量中功率不平衡量难以获得的问题。

1 系统惯量评估

1.1 惯量评估原理

电力系统的转动惯量表征了系统以额定速度转动时所储存的旋转动能，单个旋转部件的惯量通常用惯性时间常数H来表示，其计算公式如下：

(1)

式中：J为发电机转子的转动惯量；ωn为发电机额定转速；S为发电机的额定容量。

系统中的旋转部件如发电机转子具有旋转动能，当机端出现功率不平衡时，发电机会释放转子中的旋转动能来补偿功率不平衡量，此时，发电机转速会下降，发电机端频率下降，发电机转子运动方程如下：

(2)

式中：H为发电机惯性时间常数；f为机端频率；Pm，Pe分别为发电机的机械功率和电磁功率。

当系统发生扰动，出现功率不平衡时，在系统调速器作用前，系统中具有旋转动能的部件会释放转子动能来补偿功率缺额，系统频率下降，频率跌落速度与系统功率不平衡量满足如下关系式：

(3)

式中：Hsys为系统等效惯性时间常数；fCOI为系统等效惯性中心频率；ΔP为系统功率不平衡量。系统等效惯性中心频率fCOI由系统各发电机机端频率聚合到等效惯性中心得到，计算公式如下：

(4)

式中：n为发电机台数；Hgi，fgi分别为发电机i的惯性时间常数和机端频率，i=0,1,2,…，n。

由式(3)可以得到，系统的等效惯性时间常数的计算公式如下：

(5)

由式(5)可知，若发生扰动后，系统总的功率不平衡量和系统频率可测，则可以利用扰动后数据计算系统等效惯性时间常数。随着PMU技术的不断发展，对系统运行状态的实时同步监测已经逐步实现，也为利用上述方法评估系统惯量水平奠定了基础。

1.2 分区域惯量评估

上述分析建立在未考虑频率分布特性这一基础上，为系统总的惯量水平结果，伴随着大规模互联电网的出现和新能源机组的大量接入，系统惯量分布不均的特征日益明显，受扰后的电力系统动态频率响应表现出很强的时空分布特征。已有许多文献对于全系统的转动惯量进行了评估，实际上，各区域转动惯量的分布不同也会对系统的频率响应特性造成影响,文献[15]基于仿真分析了这一影响。因此，有必要考虑系统分区，得到系统不同位置的惯量分布水平。

如图1所示，为一个多区域系统，区域间通过联络线相连，进行功率交换。以该系统例，分别对各区域进行分析，求取其惯性时间常数。

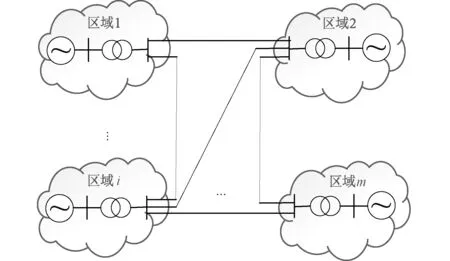
图1 多区域电力系统Fig.1 Multi-area power system

对各区域来说，扰动发生后，系统惯量与功率不平衡量、频率变化率满足式(3)，有如下关系：

(6)

式中：Hi，fi，ΔPi分别为区域i的等效惯性时间常数、等效惯性中心频率、功率不平衡量，这里i=1,2，…，m，m为区域数量。

考虑到相对于电磁功率，机械功率具有变化缓慢的特性，在系统调速系统作用前，可认为机械功率基本不变，则区域功率不平衡量可由式(7)得到：

ΔPi=Pmi-Pei=Pei0-Pei

(7)

式中：Pmi，Pei分别为故障后区域i的机械功率和电磁功率；Pei0为故障前区域i的电磁功率，在故障发生前，其与区域i的机械功率平衡。

由式(7)可知区域不平衡功率可通过求取该区域扰动发生前后电磁功率的差值来进行计算，对非故障区域，其电磁功率变化即为联络线上功率的变化，对于故障区域，其电磁功率变化为联络线上功率变化与区域内部扰动功率之和，如式(8)所示，这里带有上角标*表示为故障区域对应电气量。

(8)

式中：Pli0，Pli分别为扰动前和扰动后区域i的联络线功率；ΔPs为扰动功率。

需要注意的是，扰动发生后，系统中的不平衡功率不仅仅由区域中的发电机转子惯量释放旋转动能来承担，也包括了感应电机负荷为系统提供的惯量响应，新能源机组的调频策略也会给系统提供综合惯量。结合式(6)～式(8)，可以得到各区域的惯量计算公式如式(9)所示。

(9)

由式(9)可知，利用各区域与外界相连的联络线上功率、各区域频率和扰动功率，可以计算各区域惯量，其中，对于故障区域，需要获得扰动功率的大小，计算得到的系统惯量包括发电机、负荷等的影响。利用PMU装置，联络线上功率、系统频率等易于测量得到，而扰动功率由于扰动位置、扰动类型未知等因素常常难以通过测量得到，使得上述惯量估计方法存在一定局限性，针对此问题，本文采用一种差值法来计算区域惯量。

1.3 差值法计算分区域惯量

由式(9)可知，计算不同区域的惯量水平需要获得的测量量为各区域与外界相连的联络线上功率、各区域频率和扰动功率，扰动功率大小常常难以测量，因此本文采用一种差值法，利用故障后两个时刻的对应电气量的差值来进行区域惯量计算，该方法不需要已知扰动功率发生区域及扰动功率的大小，减少计算所需测量量。对于各区域，按照式(9)取故障后两个时刻t1，t2分别计算区域惯量，对于故障区域和非故障区域，分别为

(10)

(11)

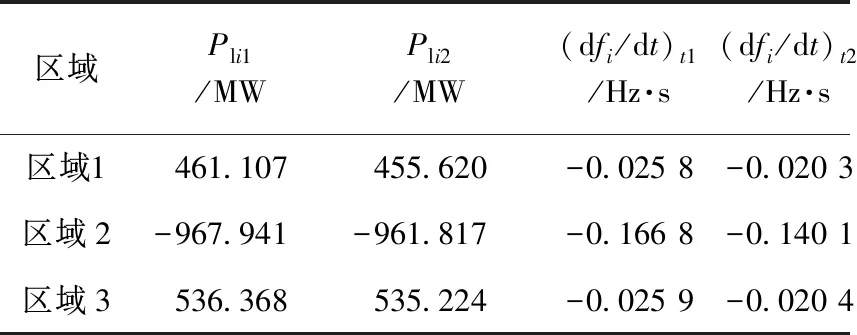
式中：Pli1，Pli2，(dfi/dt)t1，(dfi/dt)t2分别为扰动后两个时刻t1，t2对应的区域i的联络线功率和频率变化率。需要注意的是在这里，t1，t2都需要取在扰动发生后初始时间段，系统一次调频动作前。

分别对式(10)、式(11)中两个时刻对应的右侧分子分母作差值，得到各区域的惯量的表达式如式(12)所示：

(12)

由式(12)可以看到，利用两个时刻的差值计算区域惯量，故障区域和非故障区域的惯量有相同的计算公式，且计算所需的量为区域与外界相连的联络线上功率、各区域频率，不需要分辨系统发生功率扰动的区域和扰动功率大小。

1.4 数据处理

(1)数据预处理

电力系统中，利用PMU同步测量的数据进行惯量评估还存在噪声干扰、扰动时间识别等问题，需要对数据进行预处理。文献[9]对系统故障下的频率信息进行频域分析，得出暂态噪声信号频率均高于0.5 Hz，可以用低通率滤波器对频率进行滤波处理，获得平滑的频率曲线，文献[6]采用了一种去趋势波动分析法，实现扰动发生时间的识别，提高惯量评估精度。

(2)计算数据处理

为了避免某个测量点造成的偶然误差，这里的Pli1，Pli2，(dfi/dt)t1，(dfi/dt)t2均取一个时间窗内对应测量量的平均值，如图2所示，图中n为每个时间窗内取值个数，Δt为两个测量点之间的时间间隔，区域与外界相连的联络线上功率、各区域频率均取t1-tn1，t2-tn2这两个时间窗里n个测量点的平均值。

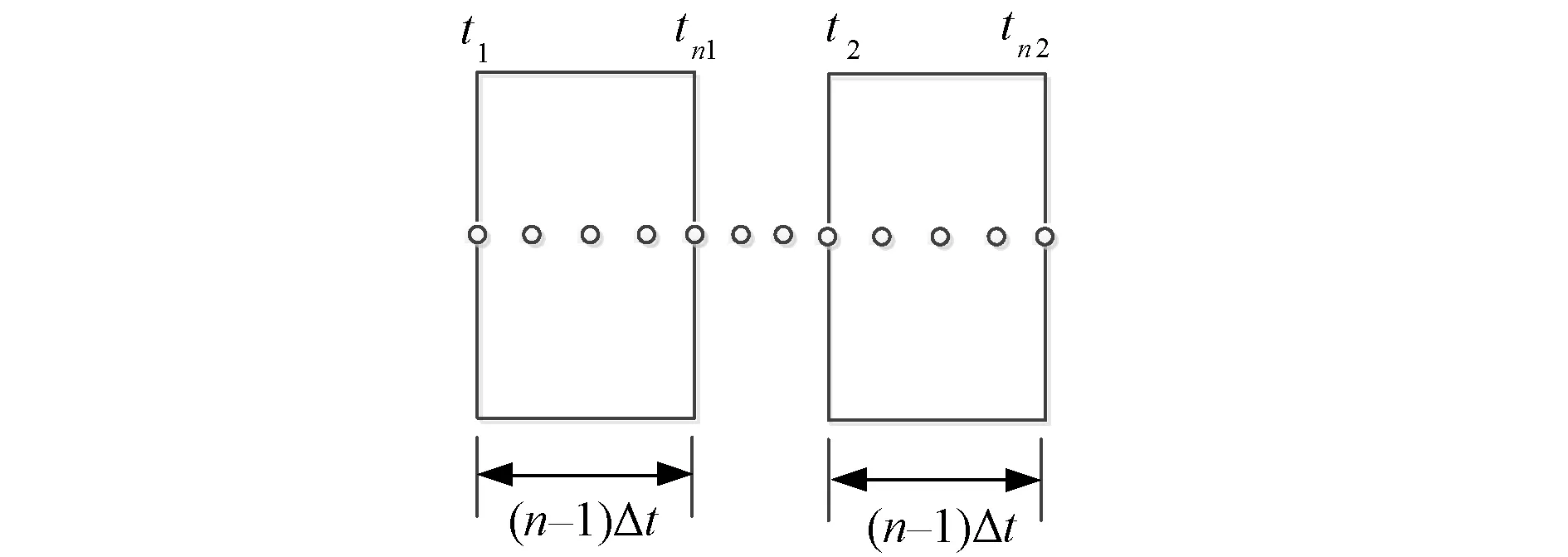
图2 电气量取值时间窗Fig.2 Time window of disturbance data

2 算例分析

以EPRI-36节点系统为例，验证所提方法的正确性。EPRI-36节点系统中有8台发电机组，包含多种机组类型。扰动发生后，不同区域机组转子运动存在差异，从而频率响应分布不同，可以用于分区惯量评估。采用EPRI-36节点系统进行分析能很好地验证本文所提方法在含多种发电类型的互联系统中的适用性。对EPRI-36系统分为3个区域处理，在PSASP软件中建立仿真模型，获取系统故障后扰动数据，采用本文所提的惯量估计方法，需要采集的数据包括：区域间联络线上功率、各区域惯性中心频率，这里各区域惯性中心频率按式(4)进行计算，由区域内发电机机端频率加权获得。将惯量评估结果与理论值进行比较，以验证本文所提出方法的正确性。EPRI-36节点系统如图3所示，分区情况如表1所示[16]。

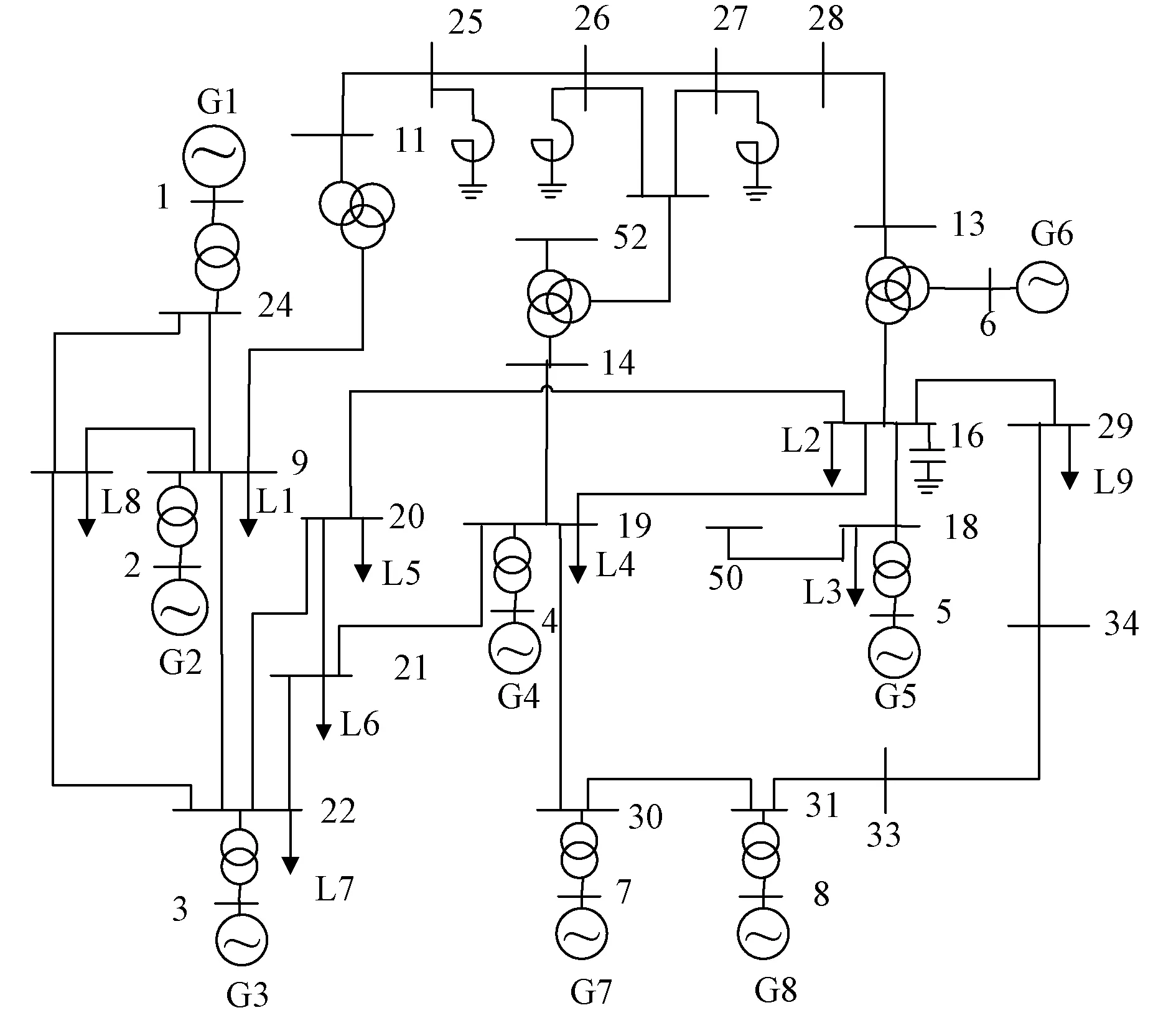
图3 EPRI-36节点系统Fig.3 EPRI-36 buses system

区域发电机联络线情况区域1G1,G2,G3通过bus25-26,bus22-20,bus22-21线路与区域2相连区域2G4,G5,G6通过五条联络线分别与区域1,区域3相连区域3G7,G8通过bus30-19,bus33-34线路与区域2相连

系统中机组总装机容量为4 150 MW，负荷2 568 MW，设置故障1为5 s时系统在节点50处增加负荷50 MW。为了考虑除发电机外其他因素如负荷等对于系统惯量的影响，分以下几种情况按照式(12)计算各区域惯量：

情况1：系统中负荷均为恒功率负荷；

情况2：系统中负荷均为感应电机负荷；

情况3：将发电机惯性时间常数设置为2倍，系统中负荷均为恒功率负荷；

情况4：将发电机惯性时间常数设置为2倍，系统中负荷均为感应电机负荷。

情况1中系统机端频率如下图4所示，考虑到t1,t2均需取在系统一次调频动作前，参考2.3节方法，以及PSASP软件中设定的仿真步长0.01 s，本文选取的两个时间段为故障发生后0.06～0.10 s和0.16～0.20 s，每个时间段内的数据点个数为5，相应的时间段内的功率和频率变化率Pli1，Pli2，(dfi/dt)t1，(dfi/dt)t2均取5个测量点的平均值，不同情况下得到的联络线功率和区域频率如表2所示。采用本文提出的评估方法，不同情况下系统的惯量评估计算结果如表3所示，这里，惯性时间常数均以100 MW为基准来表示。

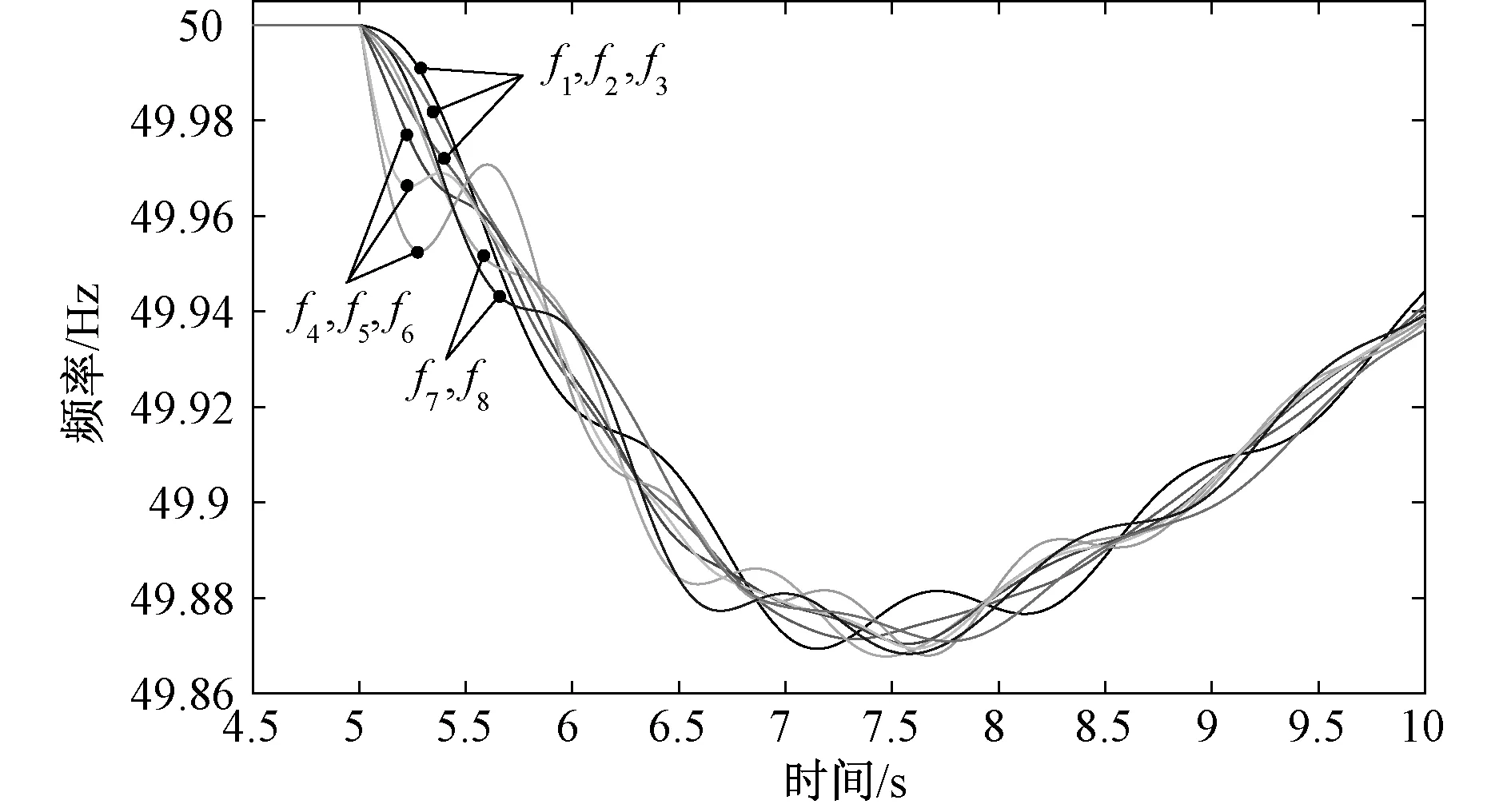
图4 故障1系统机端频率Fig.4 Frequency of generators in case 1

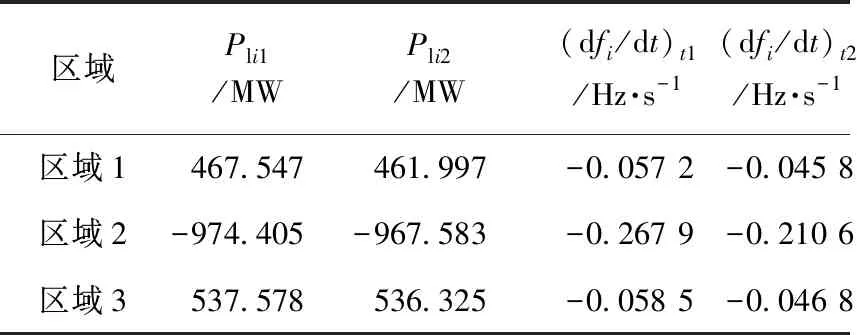
区域Pli1/MWPli2/MW(dfi/dt)t1/Hz·s-1(dfi/dt)t2/Hz·s-1区域1467.547461.997-0.057 2-0.045 8区域2-974.405-967.583-0.267 9-0.210 6区域3537.578536.325-0.058 5-0.046 8

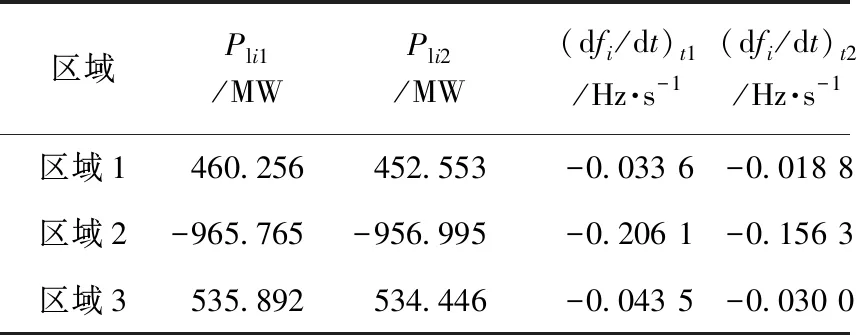
(b) 情况2中扰动数据

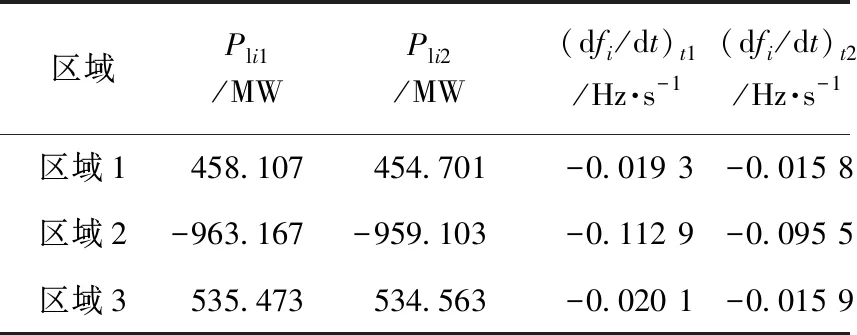
(c) 情况3中扰动数据

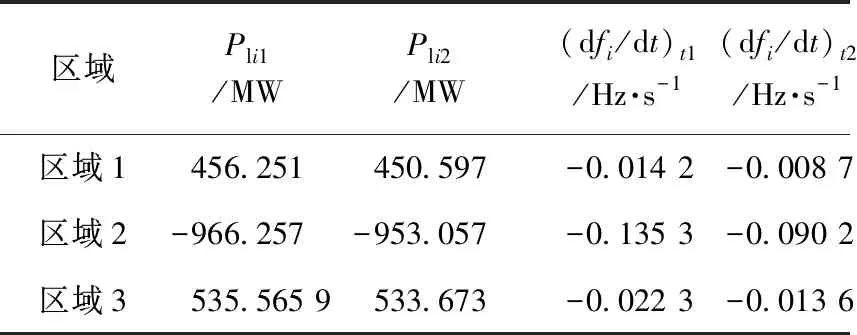
(d) 情况4中扰动数据

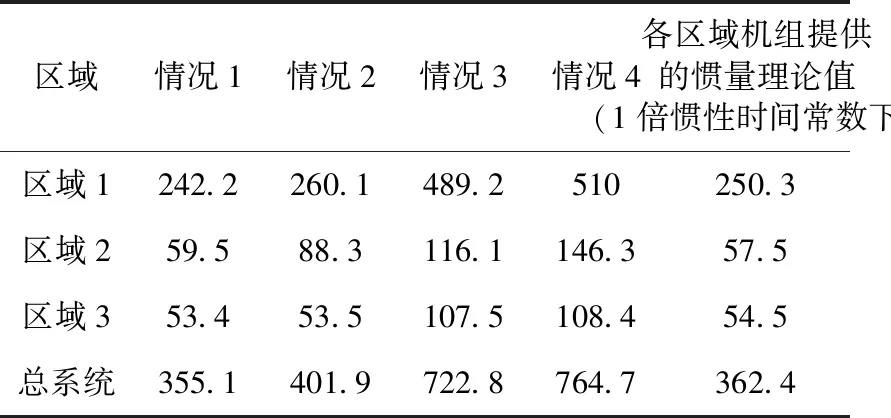
表3 故障1不同系统条件下惯量评估结果

由计算结果可以看到，情况1和情况3当系统中负荷均为恒功率负荷时，按式(12)计算区域惯量，得到的各区域等效惯性常数接近理论值，且当机组惯性时间常数变为2倍时，计算结果约为1倍惯性时间常数情况下2倍；从情况2和情况4的计算结果可以看出，当系统中接入负荷为感应电机负荷时，各区域等效惯性常数计算结果大于发电机组所提供的惯性时间常数，此时，系统中的感应电机负荷也在扰动发生初期为系统提供了一部分惯量支撑，这里负荷等因素为系统提供的惯量约为30～45 s。根据感应电机负荷的转子惯性时间常数，按加权方法得到负荷转子的等效惯性时间为51.36 s，研究表明，异步电机对电网表现出的有效惯量受转子转速和转差频率的共同调节作用，与电机转子惯量存在一定偏差[17]，考虑这些因素的影响，在一定误差范围内，采用本文所提方法能较为准确地评估包括负荷贡献在内的系统惯量水平。

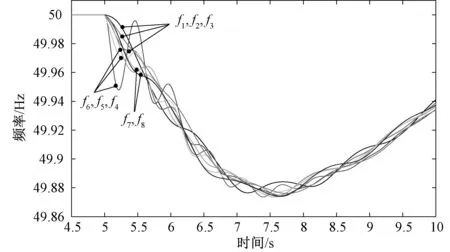
图5 故障2系统机端频率Fig.5 Frequency of generators in case 2

由图4系统的频率响应曲线可以看到，扰动发生初期，靠近扰动点、惯量水平低的区域初始频率跌落速度更快，这也说明了系统频率响应情况与区域惯量水平相关。

进一步设置故障2：发电机4在5 s时失去30%的发电量，情况1中系统机端频率如图5所示，不同情况下得到的联络线功率和区域频率如表4所示，同样利用扰动后的数据计算得到不同条件下系统的惯量结果如表5所示。

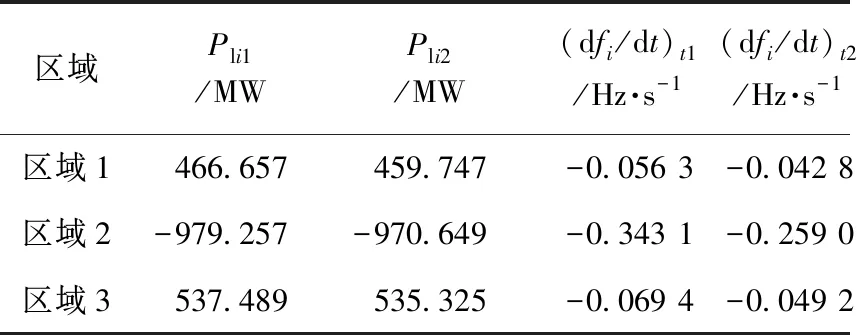
表4 故障1中系统联络线功率和区域频率

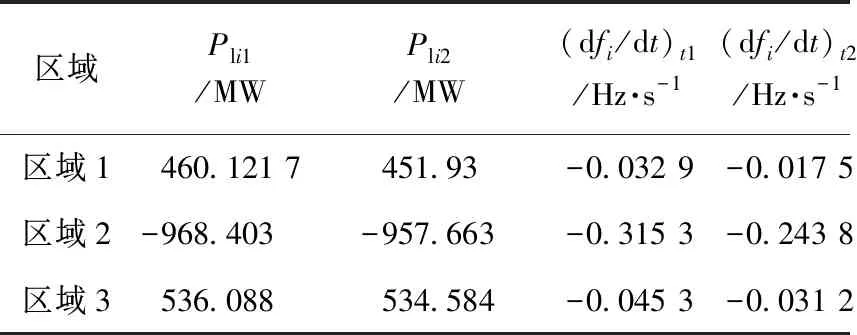
(b) 情况2中扰动数据

(c)情况3中扰动数据

(d) 情况4中扰动数据

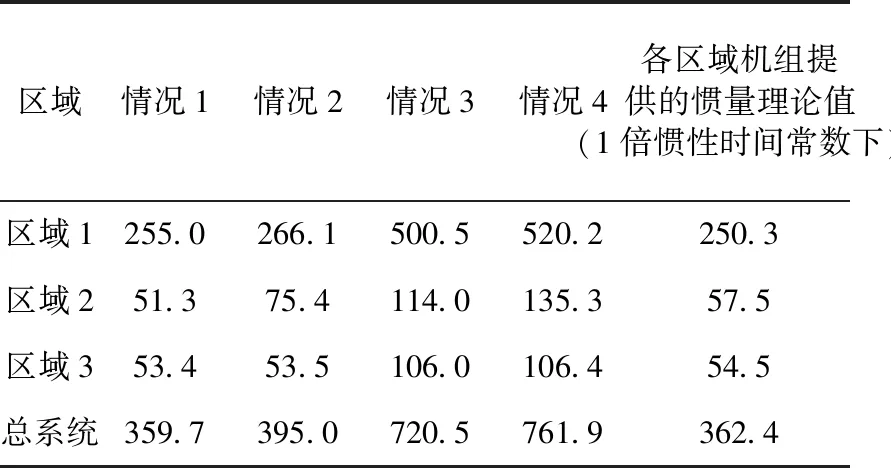
表5 故障2不同系统条件下惯量评估结果

可以看到，与故障1相同，在发电机失去部分发电量的情况下，情况1和情况3的惯量计算结果接近机组提供惯量的理论值，情况3中，发电机机组惯量设置为2倍时，得到的惯量估计结果也约为2倍，情况2和情况4中，惯量计算结果高于机组提供的惯量，负荷等因素提供的惯量约为30～45 s，同样接近负荷惯量的加权值。由图5系统的频率响应曲线可以看到，靠近扰动点、惯量水平低的区域初始频率跌落速度更快。

PMU在电网中的大量装备，为系统发生扰动后功率、频率等电气量的同步测量提供了基础。本文提出了一种基于PMU同步测量的惯量估计方法，利用PMU测量扰动后联络线上功率和各区域频率，采用差值法进行分区惯量评估，能较为准确地估计出系统各区域惯量水平。通过分析各区域惯量水平和频率响应情况，可以看到，惯量水平较高的区域在扰动发生初期能为系统提供更大的惯量支撑能力，对于频率变化的抑制能力更强，频率变化率更小。准确评估系统各区域惯量水平，有助于了解系统不同区域的频率调节能力，对于新能源高渗透率电力系统的新能源接入规划、系统的调频策略制定等都具有重要意义。随着系统的各种负荷，电力电子装置等的接入，其对于故障后系统频率响应的影响也不能忽视，采用本文所提方法，能利用较少数据计算得到各种发电机和负荷等综合作用因下的惯量结果，使系统的惯量评估更简单准确。

3 结 论

本文提出了一种基于PMU同步测量的分区惯量估计方法，对系统进行分区，利用扰动后各区域间联络线上传输功率和系统频率，能准确评估系统不同区域的惯量水平，且能计及除发电机外其他负荷因素的影响。计算过程中采用了一种差值法，对于故障区域与非故障区域均有统一的计算方法，不需要已知故障功率的大小，减小了测量及计算的复杂度。在EPRI-36节点系统中设置负荷突增与发电机失去部分发电功率两种故障，利用扰动后的数据进行分区域惯量评估，验证了所提方法的正确性。准确评估系统惯量，对于系统的新能源接入、调频策略都具有指导作用。如何进行系统分区，并指导系统PMU测量装置的安装点，测量系统中的功率和频率等电气量，是之后需要进一步研究的方向。