基于互信息变量选择与LSTM的电站锅炉NOx排放动态预测

杨国田， 王英男， 李新利， 刘 凯

(华北电力大学 控制与计算机工程学院， 北京 102206)

0 引 言

燃煤过程中产生的NOx是大气污染物的重要来源，严重影响人类健康和空气质量。2011年，环保部颁布了新的污染物排放标准，要求燃煤锅炉NOx排放不超过100 mg /m3[1]。随着NOx排放标准的提高与排放量限制线的降低，对NOx的实时监测与控制成为了评价火电机组的清洁生产的重要指标。但现有的测量设备难以满足实时测量的要求，监控难度大[2]。因而，建立高精度实时预测的NOx排放模型，实现对NOx排放的快速、有效监测十分必要。

燃煤锅炉NOx的生成机制非常复杂，受燃煤特性、炉内温度和配风方式等多种因素的影响，这些变量间相互耦合，难以用简单的机理模型描述。因此，多数研究者通过机器学习算法建立基于热工过程参数的NOx排放预测模型。文献[3-5]引入了神经网络(artificial neural network，ANN)建立了电厂锅炉运行数据和NOx排放量之间的关系。文献[6,7]采用支持向量机(support vector machine，SVM)对NOx排放进行建模，由于支持向量机具有良好的非线性映射能力，使模型具有较好的预测性能。J. Smrekar针对燃煤锅炉NOx排放问题，构建了一种基于静态ARX的多步预测模型[8]，并通过交叉验证对模型的输入变量进行了筛选，取得了较好的预测效果。牛培峰等利用极限学习机(Extreme Learning Machine，ELM)建立NOx排放模型[9,10]，并结合优化算法，对模型参数进行搜索和优化，提高了网络的学习速度。然而，上述方法只实现了对NOx预测的静态建模，但在实际运行过程中影响NOx排放的多个过程参数与NOx排放测量存在较大的延迟，而且校准它们之间的准确对应关系十分困难，因此所建立的NOx排放静态预测模型的精度往往难以满足要求。同时在基于机组历史运行数据进行NOx排放建模中，选择影响NOx排放的特征变量至关重要。由于机组的历史运行数据通常耦合较严重且信息量和变量规模较大，预测模型准确度受选择特征变量的直接影响。模型的复杂度和训练的时间取决于特征变量的数目，高维的特征变量会知道导致模型训练时间增多，结构更复杂，且更容易引入噪声，导致模型精度降低；而特征变量少选或漏选将会导致模型不够精确，预测性能随过程时变而下降。目前NOx排放预测特征选择一般通过分析NOx生成的相关机制，选择合适的特征变量进行建模，以减少特征变量的数目。

伴随着大数据时代的到来，深度学习模型逐渐被应用到时序数据的研究中。深度学习作为一种基于对数据进行高度表征的学习方法，能够对输入信号逐层抽象并提取特征，挖掘出更深层次的潜在规律[11]。长短期记忆(long-short term memory, LSTM)是一种著名的深度学习模型。它将时序的概念引入到网络结构设计中，其内部有自循环，允许数据在网络中循环流动，可以保存之前的信息供将来使用，对时间序列数据具有强大的处理能力。近年来，在电力负荷预测[12]，自然语言处理[13]、机器翻译[14]等不同领域中，均利用LSTM模型实现了良好效果。基于互信息进行特征变量选择是一种新型的变量选择方法，其中互信息量化并计算了不同相关变量之间的关联性，可以在线性空间或者非线性空间中描述变量之间的关系。本文提出一种基于互信息变量选择和长短期记忆网络的NOx动态预测算法。首先基于互信息“最小冗余最大相关”准则对原始数据集进行筛选和重要性排序，获取以互信息值为度量标准的变量集。然后输入至预测模型，并采用多层网格搜索对LSTM的参数进行优化，建立NOx排放动态预测模型。最后采用某660 MW超超临界燃煤机组历史数据实现对NOx排放动态预测模型的验证。

1 LSTM网络

在循环神经网络(Recurrent Neural Network, RNN)的基础上，Schmidhuber和Hochreiter改进了神经网络的时间递归细胞，解决了RNN使用过程中所产生的梯度消失、梯度爆炸以及缺乏长期记忆能力等问题，并在1997年正式提出长短期记忆(Long Short- Term Memory，LSTM)神经网络，使得循环神经网络能够有效地运用于长跨度的时序信息[15]。

LSTM是一种特殊的RNN。RNN的核心为循环，在信息的传递链中，经过每次循环时会有部分信息仍然被保留在隐含层的神经元中，并与新的信息一起作为输入进入下一个神经元。所有 RNN 都是一种具有重复模块的链式形式，LSTM的隐含层重复模块A被称作记忆模块，如图1所示。LSTM独特的记忆细胞和门机制，可以对RNN的序列化输入进行处理，因此有效的避免了RNN在任意时间长度序列下产生的长期依赖关系，并解决了RNN进行反向误差传播算法(Back Propagation Through Time，BPTT)训练过程中回传残差使指数下降所产生的梯度弥散问题。

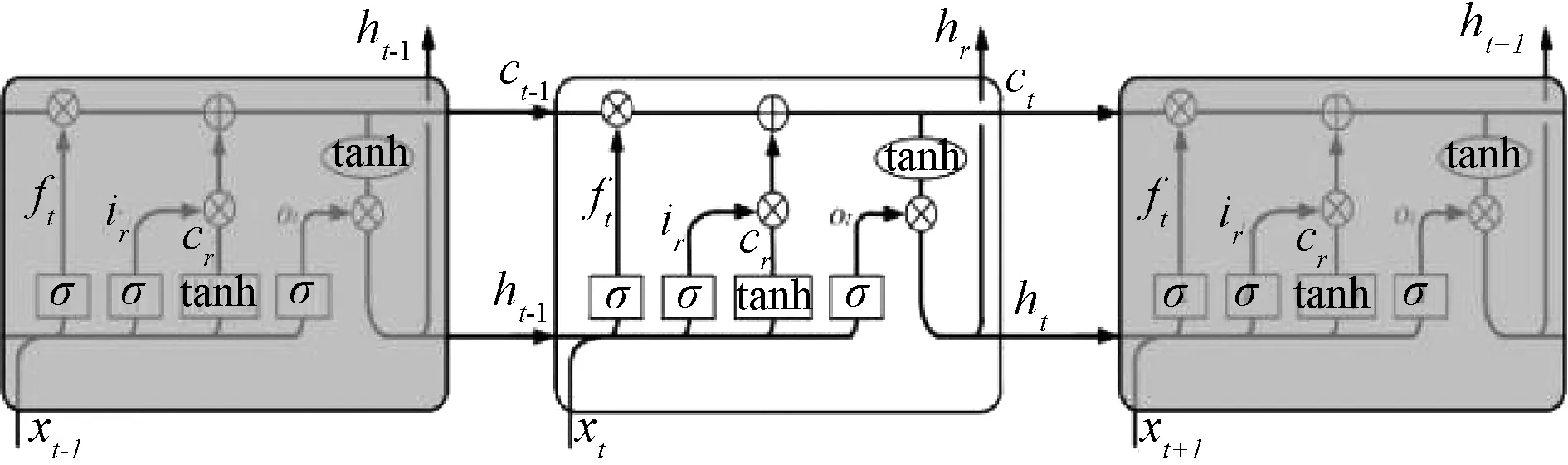
图1 LSTM网络结构Fig.1 Structure of LSTM

LSTM神经网络控制门包含输入门(input gate)、遗忘门(forget gate)和输出门(output gate)，其中遗忘门是决定神经元之间信息传递过程中是否保留的关键部分。每个门结构都各自配备一个乘法器，实现对信息的输入和输出以及每个细胞的状态的控制。LSTM 工作流程如图1所示，当前时刻的xt和上一时刻LSTM隐藏状态ht-1这两类信息通过三个“门”结构输入到当前时刻的LSTM，每个“门”的激活状态根据其逻辑函数对输入信息的计算而判断。经过非线性函数的变换后的输入门的输出，叠加上遗忘门处理过的记忆单元状态，形成新的记忆单元状态ct。最终记忆单元状态ct通过非线性函数的运算和输出门的动态控制形成LSTM单元的输出ht。各变量之间的计算公式如下：

it=σ(Wixt+Uiht-1+Vict-1+bi)

(1)

ft=σ(Wfxt+Ufht-1+Vfct-1+bf)

(2)

ct=ft·ct-1+it·tanh(Wcxt+Ucht-1+bc)

(3)

ot=σ(Woxt+Uoht-1+VoCt+bo)

(4)

ht=ot·tanh(ct)

(5)

式中：ht表示t时刻计算单元的输出；ct、it、ft、ot分别表示t时刻LSTM细胞、输入门、遗忘门和输出门的计算规则；W、U、V均为参数矩阵；b为偏置项；σ(·)和tanh(·)为激活函数。

LSTM预测模型中，涉及到众多参数，其中学习速率、隐含层神经元数目和时间步长最为关键[16]。为了达到更好的预测效果，本文采用网格搜索的方法对模型参数进行寻优。网格搜索是一种简单实用、容易并行计算且计算耗时可控的优化方法[17]，能够很好地满足任务需求和实验要求。

2 基于互信息的变量选择

2.1 互信息

信息熵理论由Shannon在1948年提出，信息熵的提出解决了信息的量化表达问题。互信息(Mutual Information, MI)在信息熵的基础上进一步计算了两个变量之间的信息包含量[18，19]。因此变量之间相关度的大小可以通过MI值标定。

随机变量X信息熵的计算公式为

(6)

式中：H(X)代表X的信息熵，X不同取值下的概率分布为P(X)。

设离散型随机向量(X,Y)的联合概率分布为P(X,Y)，则(X,Y)的二维联合熵定义为

(7)

如果假设随机变量X和Y的边际分布分别为P(x)和P(y)，可定义在已知随机变量X的条件下，随机变量Y的条件熵H(Y|X)为

(8)

H(X|Y)≤H(X)说明Y中包含了X的某些信息，该部分信息称为互信息I(X,Y)，计算公式如式(9)所示。

I(X,Y)=H(X)-H(X|Y)

(9)

通常情况下，X、Y的概率分布未知，则互信息如式(10)所示。

(10)

2.2 变量筛选规则

变量的筛选依据是互信息准则，即在保证待选特征变量与主导变量之间互信息最大的前提下，同时期望待选变量与已选变量之间的互信息之和最小。因此，选择如下评价函数

(11)

式中：fi∈F为待选变量；c为主导变量；Sj∈S为已选变量；β为惩罚因子。其值越大，候选变量与已选变量之间的信息冗余性则越需要考虑进变量筛选的过程中。

根据互信息进行变量筛选步骤如下：

Step1：选择输出变量Y与输入样本X=[x1,x2,…xk]，k表示输入变量特征个数。

Step2：根据直方图概率密度估计计算输出变量Y的概率分布函数PY(x)。

Step3：根据直方图概率密度估计计算某特征变量xi的概率分布函数Pi(x)。

Step4：计算特征变量xi关于输出变量Y的互信息I(xi,Y)。

Step5：重复步骤3、4，获得样本X所有特征变量关于Y的互信息向量P=[p1(x),p2(x),…pk(x)]。

Step6：计算所有特征变量关于输出变量Y的评价函数，根据评价函数进行变量筛选，获得变量筛选向量J=[J1(x),J2(x),…Jk(x)],{Ji(x)>Jk(x),i>k}。

3 MI-LSTM预测模型

为了降低预测模型复杂度，提高NOx预测精度，本文提出基于互信息变量选择和长短期记忆神经网络(MI-LSTM)的NOx排放动态预测模型，如图2所示。 首先，利用互信息筛选原始特征集，得到以MI值为度量标准的特征序列子集；然后，基于LTSM建立NOx排放模型，使用网格搜索算法确定最优超参数集，以预测模型的RMSE为指标，开展前向特征选择，获取最优特征子集；最后，以最优特征子集构建LSTM预测模型，动态预测NOx排放。

图2 基于MI-LSTM的NOx排放模型Fig.2 Structure of MI-LSTM model

3.1 建模步骤

基于MI-LSTM的NOx排放动态预测模型建模步骤如图3所示。

图3 基于MI-LSTM神经网络的NOx预测模型流程图Fig.3 Prediction flow chart of NOx based on MI-LSTM neural network

3.2 模型评价方法

本文使用以下3类指标衡量模型预测精度。

平均绝对误差(Mean Absolute Percentage Error，MAPE)是单个观测值与算术平均值之间偏差的绝对值平均，可以准确反映实际预测误差的大小。

(12)

皮尔逊相关系数(Pearson Correlation Coefficient，R)是用来描述两组数据一同变化移动的趋势。

(13)

标准误差(Root Mean Square Error，RMSE)，也称为均方根误差，它对预测数据中的特大或特小误差反映非常敏感，因此能够很好地反映预测的精确度。

(14)

4 NOx排放的MI-LSTM建模与测试

4.1 研究对象

本文研究的对象是河南某燃煤电厂660 MW机组，锅炉为DG2060/26.15-Ⅱ2型超超临界参数变压运行直流炉。锅炉燃烧方式为前后墙对冲燃烧，共布置6层燃烧器(前后墙各3层)，每层各有6只旋流燃烧器，前墙从下往上依次为A、B、C层，后墙从下往上依次为D、E、F层，每台中速磨煤机为同层的6只煤粉燃烧器提供风粉混合物。同时各布置1层燃尽风在前、后墙旋流煤粉燃烧器上方，其中每层6只燃尽风(AAP)喷口、2只侧燃尽风(SAP)喷口。

从电厂监控信息系统((supervisory information system，SIS))中采集历史数据进行挖掘与预测，采样周期为1 min，负荷跨度为 300～660 MW。计算各采集变量与NOx排放量互信息，按照互信息从大到小排序后选择前27个变量作为输入变量，其互信息见表。主导变量为选择性催化还原(selective catalytic reduction，SCR)反应器入口处NOx浓度。所采集的3 500组数据分为测试集和测试集两部分。其中，选取3 000组的数据用来建立基于MI-LSTM的NOx排放量预测模型，其余500组数据作为测试集，用来验证模型的准确度和泛化能力。

4.2 基于MI-LSTM的NOx排放建模

利用序列前向选择方法选择最优特征子集，输入变量按互信息输出由大到小排序，变量数目从3到27以2为差值递增，同时针对LSTM网络的时间步长、学习速率和隐层神经元数目3个重要参数进行网格搜索，寻找最优输入变量子集及最佳模型参数，网格搜索结果如图4所示。

图4中，横轴表示训练时间步长，纵轴表示输入特征数量个数，其中时间步长划分如表2所示，同时根据表1学习速率与隐层神经元个数获得共3×3=9组对比模型。

从图4可以看出，颜色越深代表RMSE值越低，随着特征数量的增多，RMSE的值逐渐上升，说明高维数据特征将包含大量的信息冗余，致使LSTM模型拟合效果变差。9组对比模型中，中间三组模型RMSE明显低于其他各组，表明学习速率对模型预测效果影响最大，且学习速率为0.001时，训练效果最好，模型获得较好的预测效果。

模型最佳输入变量的数目为7，筛选出最优特征变量特征子集为：后墙固定端燃尽风量、F层二次风量、E给煤机给煤率反馈、总风量、E磨一次风量、主给水温度及机组负荷。使用筛选出来的变量集合作为模型的输入，SCR反应器入口处NOx浓度为模型的输出，建立排放量预测模型。根据网格搜索结果可知，LSTM模型中超参数如表3所示。

表 1 入口变量及其互信息

表2 待网格搜索的变量

图4 特征个数对模型RMSE的影响Fig.4 Impact of number of input variables on model RMSE

参数名参数值时间步长4学习速率0.001隐含层神经元数目256迭代次数2 000Batchsize16

MI-LSTM模型测试集的预测结果如图5所示。从图中可以看出，预测值分布在理想直线附近，预测结果与实测数据吻合度高。由计算可知，模型预测误差为：MAPE=0.175%，R=0.905，RMSE=0.498。样本的预测误差很小，模型有较好的预测能力。

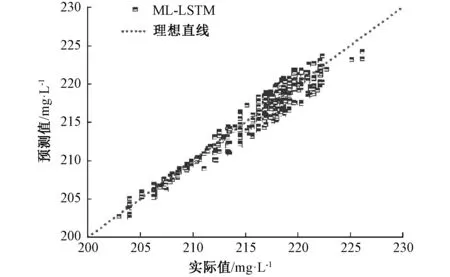
图5 MI-LSTM模型对NOx排放质量浓度的预测结果Fig.5 NOx emission predicted by MI-LSTM

4.3 模型比较

为了分析模型性能，作为对比，参考燃烧机理，选取机组负荷，给煤量，一次风量，二次风量，燃尽风量，炉膛出口烟气含氧量，总风量和主蒸汽温度共27组特征变量作为输入，使用相同的数据集建立NOx预测模型。

本文构建了其他3种模型作为对比：(1)LSTM模型；(2)MI-RNN模型；(3)MI-BP模型。LSTM是在RNN的基础上进行改进的时间递归神经网络，BP网络则是常用的NOx排放建模方法。结果如图6～9及表4所示。

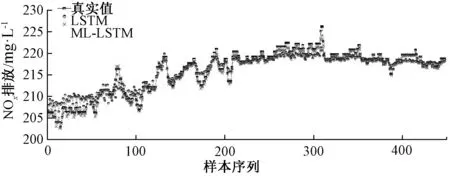
图6 MI-LSTM与LSTM模型的NOx排放预测Fig.6 Prediction of NOx emission for MI-LSTM and LSTM

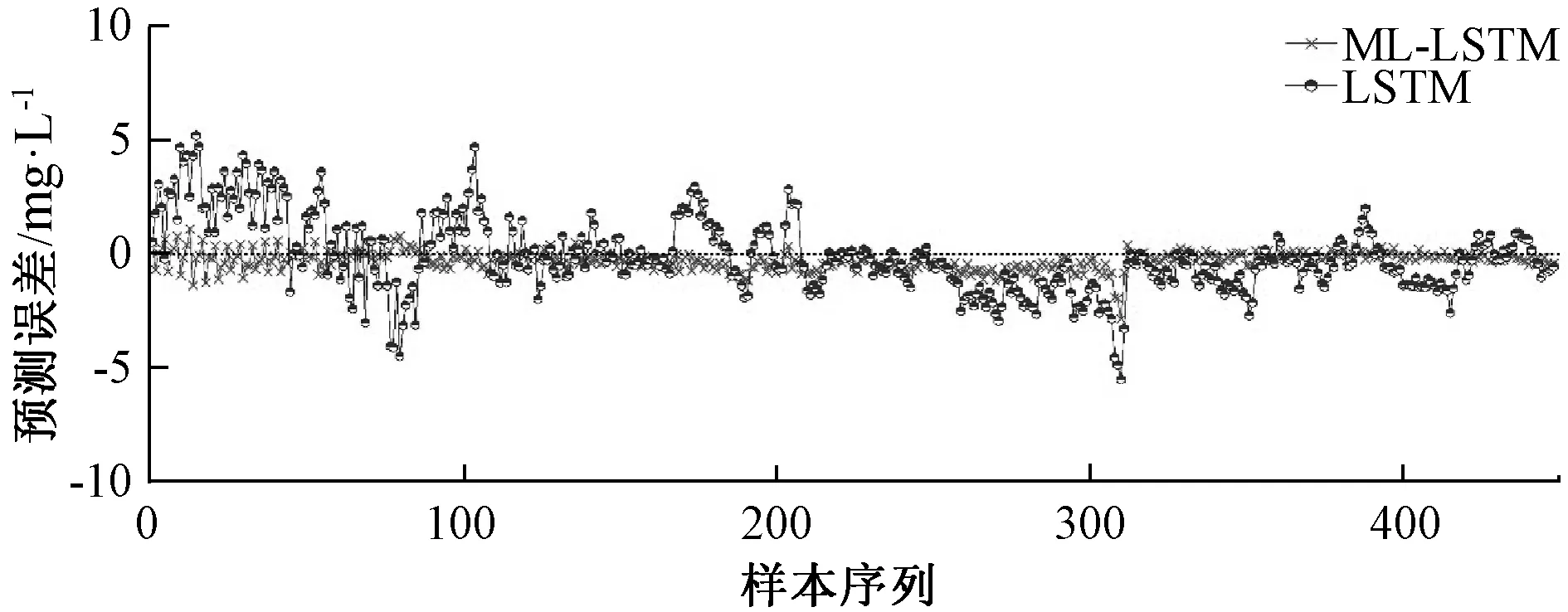
图7 MI-LSTM与LSTM模型预测误差对比Fig.7 Comparison of the prediction error for MI-LSTM and LSTM

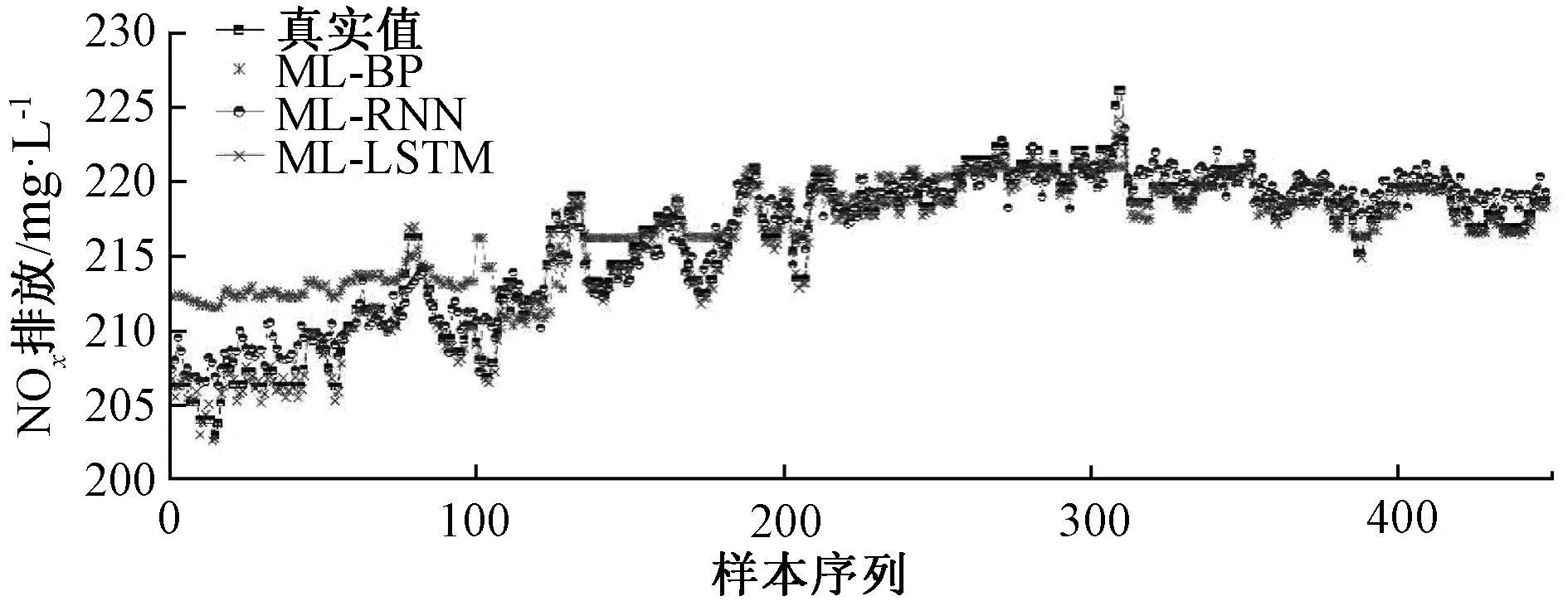
图8 不同模型的NOx排放预测Fig.8 Prediction of NOx emission using different models

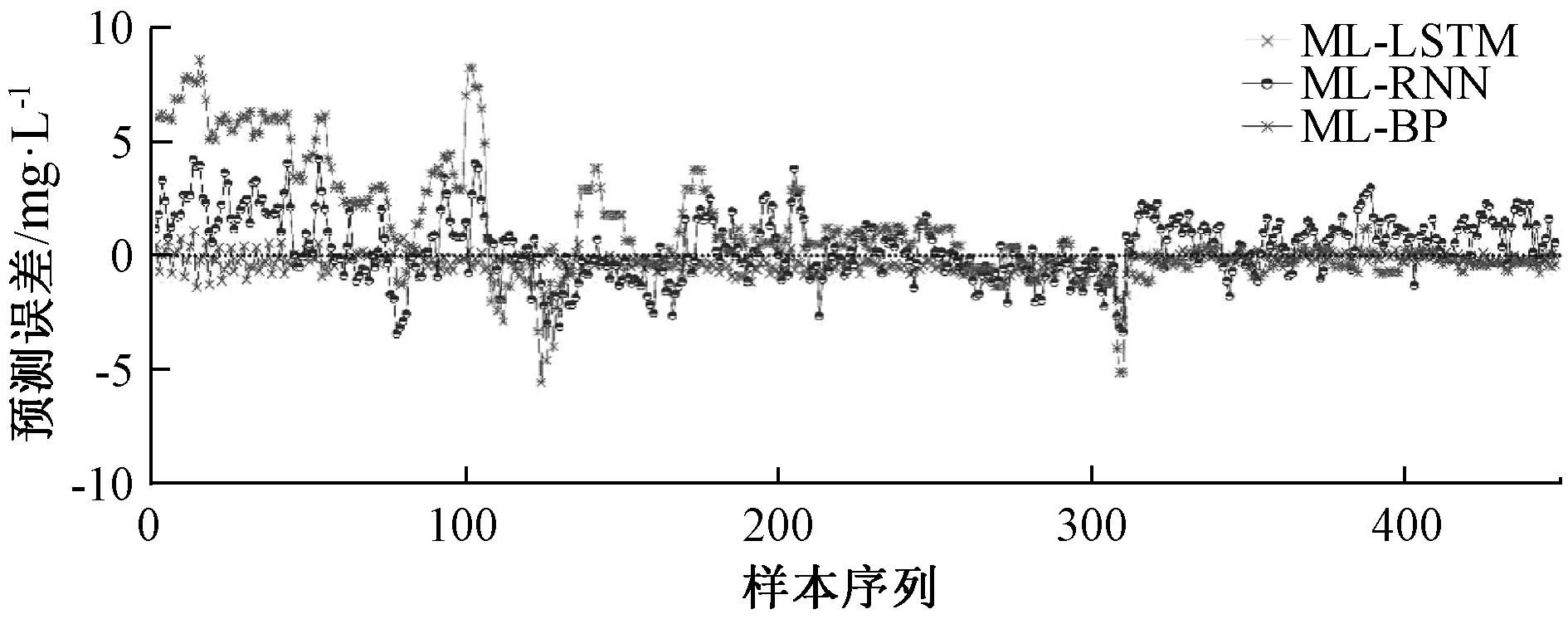
图9 不同模型预测误差对比Fig.9 Comparison of prediction error using different models

Tab.4 Comparison of prediction results of different models

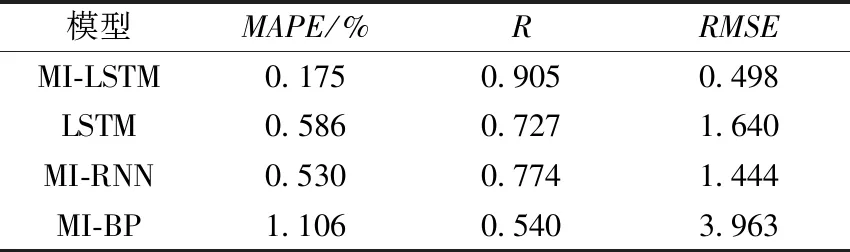
模型MAPE/%RRMSEMI-LSTM0.1750.9050.498LSTM0.5860.7271.640MI-RNN0.5300.7741.444MI-BP1.1060.5403.963

由图6和图7可知，在建立火电机组的NOx排放预测模型时，如果没有利用互信息筛选模型输入变量，直接根据机理分析建立基于LSTM的NOx排放模型，模型的预测趋势与原始数据仍相同，但其预测误差显然高于基于MI-LSTM的预测模型，这表明经互信息变量选择之后，得到了更有效的输入变量集合，减少了输入变量的个数，降低模型复杂度，提高了模型预测精度，表现出更好的泛化能力。

图7和图10分别为MI-LSTM、MI-RNN和MI-BP 3种模型的预测结果和预测误差对比图，其中LSTM和RNN均为动态深度学习网络，BP为常规前向网络由图中可知，MI-LSTM模型及MI-RNN模型的预测值准确率均高于MI-BP模型，表明了动态深度学习网络的预测结果准确率远高于传统模型，且MI-BP模型在数据量大的情况下训练时间远远高于其它两个模型。此外，在具有相同结构和模型参数时，与MI-RNN模型相比，MI-LSTM模型取得了更高的预测精度。

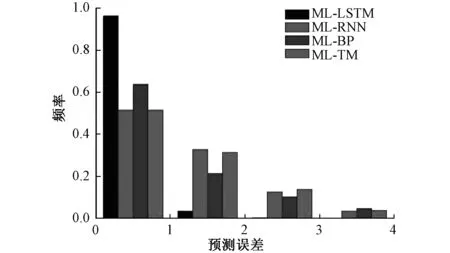
图10 误差频率直方图Fig.10 Error frequency histogram

表4和图8分别给出了不同模型的预测结果的指标对比和误差的频率直方图。由预测结果可以看出，基于互信息变量选择之后的模型，取得了更好的预测效果。MI-LSTM神经网络对火电厂NOx排放预测效果最好，误差指标RMSE和MAPE均低于对比模型；同时其相关系数R明显大于其他模型，证明数据跟踪效果明显好于其他模型，且预测结果波动较小，预测精度高。

5 结 论

针对电站锅炉NOx的排放受多个热工变量的影响，而变量间具有相关性以及现场数据的时序特性，本文提出一种基于互信息变量选择和长短期记忆网络的NOx动态预测模型。首先，使用基于互信息的变量选择算法对多个影响NOx排放的输入变量进行筛选，并采用网格搜索算法优化LSTM网络参数，建立NOx排放的动态预测模型。基于某660 MW燃煤锅炉的现场运行数据，构建了MI-LSTM、LSTM、MI-RNN和MI-BP四种NOx预测模型，仿真结果表明，与LSTM模型相比，基于互信息的变量选择算法可以减少模型输入变量个数，降低模型复杂度，提高模型精度和泛化能力；与MI-RNN和MI-BP模型相比，所提出的长短期记忆动态模型具有更高的预测精度。