基于熵产理论的LNG 液舱分层翻滚过程及特征研究

吕煜蒙，卢金树，孙俊杰

（浙江海洋大学船舶与海运学院，浙江舟山 316022）

LNG 翻滚是指由于密度变化上下两层液化天然气分层界面受到扰动而产生的一种热不稳定性现象。翻滚事故产生的主要危害是大量BOG 的迅速蒸发，导致储罐超压。自意大利的拉斯佩齐亚LNG 翻滚事故[1]发生后，几十年间共有24 起事故被记载[2]。为了研究LNG 翻滚现象，自1970 年起，相关学者进行了一系列的实验研究[3-5]，并提出了相应的理论模型[6-9]。

随着计算流体力学技术的发展，大量学者开始运用CFD 软件对LNG 翻滚过程进行动态模拟。侯金伟[10]用R-B 模型对LNG 翻滚过程进行了描述，分析了不同瑞利数下储罐内对流规律。赵晓丹[11]通过分析分界面最大速度研究了分层数、分层高度等因素对LNG 翻滚的影响。SRINIVASAN,et al[12]和WANG Zhe,et al[13]考虑了组分等因素并对LNG 翻滚过程进行了定性分析。LI Yuxing,et al[14]通过分析涡流强度等参数提出了翻滚系数，并研究了不同容积储罐的临界密度差。

综上所述，目前有关学者主要通过流体力学角度，分析分界面速度矢量等参数来揭示LNG 翻滚过程中的流动机制。但是对于LNG 翻滚诱因产生的位置及空间分布和LNG 翻滚过程的强弱程度鲜有研究。熵作为一种衡量不可逆性的分析工具，可用于衡量流体传热传质中各个位置的能量损失。熵产分析方法可以为不可逆损失的分布提供可视化窗口。因此本文将热力学第二定律的熵产分析应用于LNG 翻滚的研究中，以LNG 液舱为研究对象，基于Mixture 模型，并考虑分层密度差等影响因素，探究LNG 翻滚过程中液舱内部传热与流动过程的耦合机制。

1 模型建立

1.1 物理模型

本文研究对象选自某LNG 液舱[15]，并对其进行二维建模，见图1。由于LNG 翻滚通常发生在相邻两层之间，且本文主要研究液舱内LNG 翻滚过程中的热力学行为。故作如下假设和简化：

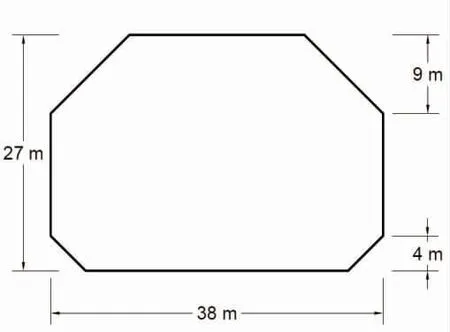
图1 液舱二维模型尺寸图Fig.1 Dimension of two-dimensional tank model

(1)假设LNG 为不可压缩牛顿流体；

(2)初始情况下LNG 分层已经产生，两层LNG 之间有固定的分界线，不考虑气相空间；

(3)忽略舱壁结构以及舱壁厚度；

(4)将LNG 组分简化为纯物质甲烷，主流区初始物性参数如表1 所示[16]。

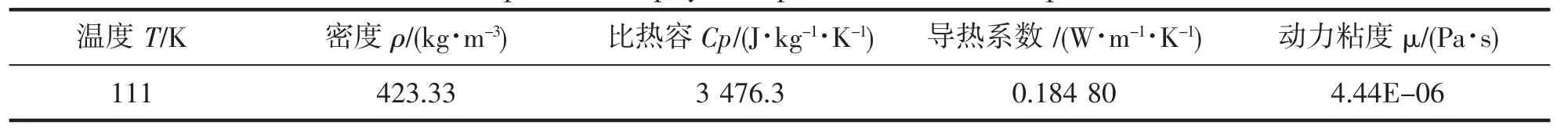
表1 甲烷物性参数与温度的关系Tab.1 Relationship between physical parameters and temperature of methane

1.2 数学模型

（2）动量方程：

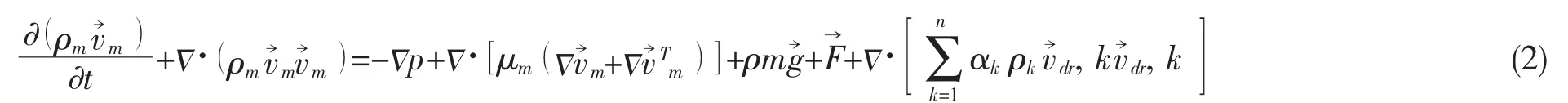
（3）能量方程：

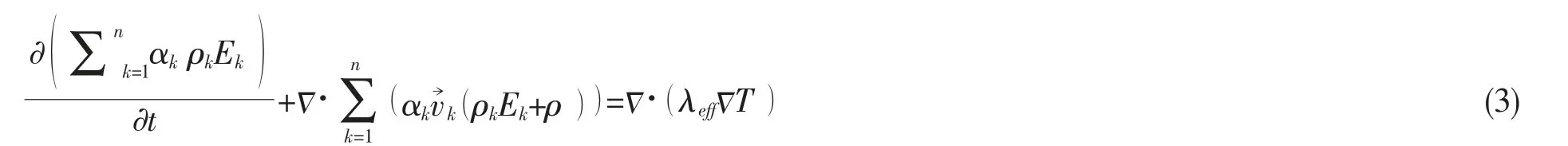
（4）第二相体积分数方程：为第k 相的体积分数。

（5）湍流方程：

Pk和μt定义如下：

式中，经验常数Cμ=0.09，Cε1=1.44，Cε2=1.92，αk=1.0，αε=1.3。

（6）熵产率方程：

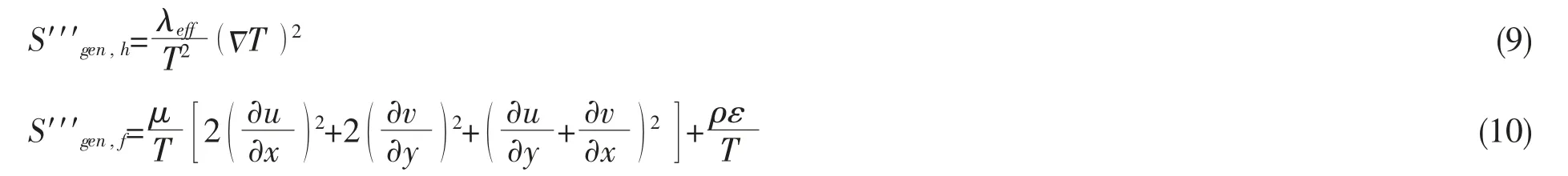
将熵产率方程进行积分可得熵产方程[17]：

S′′′gen,f为传热熵产W·K-1；Sgen,f为粘性耗散熵产W·K-1；μeff为有效动力粘度，Pa·s；ε 为湍流动能耗散率，m2·s-3，T 为工质温度，K。

1.3 数值模型

(1)网格划分

运用ICEM 软件对液舱物理模型进行建模，并采用结构性网格进行网格划分，针对液相交界面与近壁面处进行了网格加密，见图2。设置检测点P1、P2、P3，分别位于液舱中轴线底部、中部、顶部。网格模型经无关性验证，取网格数量为43 026。

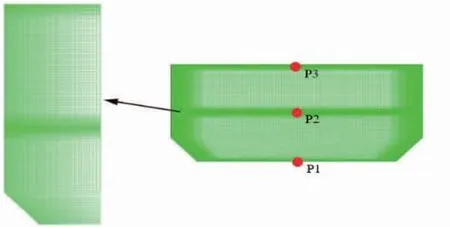
图2 结构性网格划分Fig.2 Structural meshing

(2) 边界及初始条件

本文主要研究液舱内LNG 翻滚过程中的热力学行为，忽略顶部气相空间。对于顶部壁面设置为自由滑移壁面，侧壁及底部壁面设置为绝热无滑移壁面。初始化温度：上层LNG 温度111 K，密度423.34 kg·m-3，下层LNG 温度113.017 K，密度420.34 kg·m-3，初始载液率为60% H，上下层液高均为8.1 m。

(3) 数值方法

PISO 算法包含1 个预测步和2 个修正步，其精度较高。对于瞬态问题，PISO 算法有明显的优势[18]。基于本文研究的LNG 液舱翻滚过程属于瞬态非定常问题，选用PISO 算法。梯度离散格式选用Green-Gauss Cell Based，压力离散格式为PRESTO!，其余各离散格式选用First Order Upwind，保证初期求解稳定性。时间步长选用0.001 s。

2 数值计算与结果讨论

2.1 LNG 翻滚过程与熵产分析

对于60%H 载液率的薄膜型LNG 储罐，上下两层LNG 初始密度差为3 kg·m-3，上下两层高度相同。为研究LNG 翻滚过程中的演变情况，选取了4 个不同时刻下的液舱内密度分布与LNG 流动轨迹云图，如图3所示。可以看出，由于密度差造成的界面不稳定性，在时间T=10 s 时，液舱侧壁交界面处出现了翻滚倾向，上层密集LNG 液体在侧壁处挤压下层LNG 液体。在T=100 s 时，液舱中部交界面扩散，上层密集LNG 开始向液舱侧壁移动，但该时刻下液舱近壁处的交界面仍未失稳，表明液舱内翻滚还未真正开始。随着时间推移，

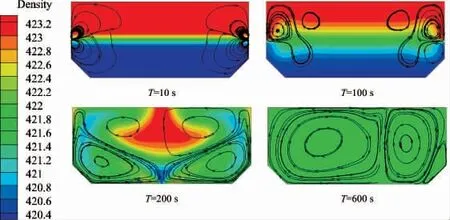
图3 密度云图Fig.3 Density contours in different times

LNG 液体开始逐步掺混，涡流影响范围开始扩大。至T=200 s 时，涡流影响至整个液舱域，上下两层LNG 开始全面混合。密度差驱动的翻滚机制作用强度逐渐减弱，至T=600 s 时，液舱内LNG 完全混合。

为了揭示LNG 翻滚过程中的传热传质机制，对以上4 个时刻进行了熵产分析，如图4、5 所示。从图4 可知，由于初期两相存在较大的温度差，在相界面处温度梯度较大，故传热熵产主要集中在相界面附近。至T=100 s 时，两相交界面开始扩散，液舱中部交界面处传热熵产率降低。但两相交界面在液舱近壁处未失稳，故仍有较高的传热熵产率。T=200 s 时刻表明，此时液舱内进行着全面翻滚，域内仍存在着较大的传热熵产率，表明LNG 还未充分混合。直至T=600 s 时刻，LNG 混合充分。从图5 可知，初始时刻液舱近壁处出现较大的粘性耗散熵产率，随着翻滚演变推进，粘性耗散熵产率云图变化趋势与上文中密度云图反映的翻滚趋势保持高度的一致性。分析可知，LNG 翻滚主要是受密度差推动的涡旋作用影响，从初期的液舱侧壁交界面处的局部湍流耗散效应，逐步演化至整个域内的湍流行为。

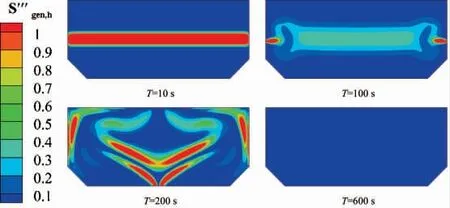
图4 传热熵产率Fig.4 Entropy production by heat transfer in different times

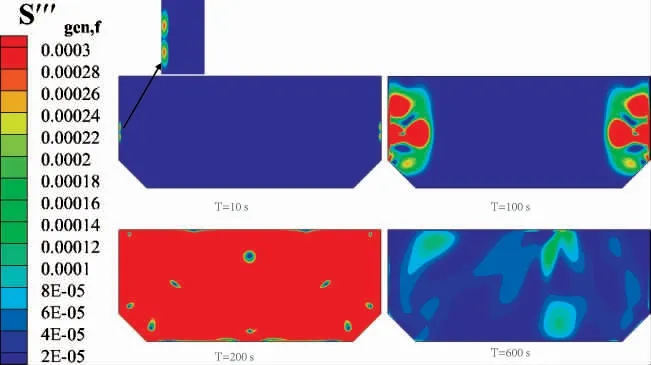
图5 粘性耗散熵产率Fig.5 Entropy production by dissipation in different times

为了更进一步地研究LNG 翻滚现象与熵产演变规律，记录监测点1、2、3 的密度波动值与其传热和粘性耗散熵产值如图6、7 所示。由图中可以看出，整体上粘性耗散熵产和传热熵产的波动演变与密度值波动演变在时间上具有一致性。从图6 中可知，0～98 s 传热熵产呈下降趋势，并在98 s 时刻，传热熵产到达波谷。结合上文云图可以得出，在该阶段，传热熵产因相界面的不断扩散而减小，但上下两层LNG 液体并未掺混。而在98～186 s 时，传热熵产急剧增加，表明在98 s 后，相界面失稳，上下两层LNG 液体急剧掺混。186～238 s 内传热熵产快速下降，表明LNG 已经进行整体掺混。随着时间推移，域内LNG 液体掺混充分，传热熵产逐渐减小。从图7 中可以看出，粘性耗散熵产的两次波峰与密度波动峰值刚好匹配。粘性耗散熵产在202 s 到达最高值，晚于传热熵产到达峰值的时间，其原因在于密度的变化受温度影响，而传热熵产是液舱内温度势的一种表现形式。至347 s，粘性耗散熵产达到第2 个波峰，结合密度波动曲线，表明在该时刻液舱还有一定强度的涡流存在。

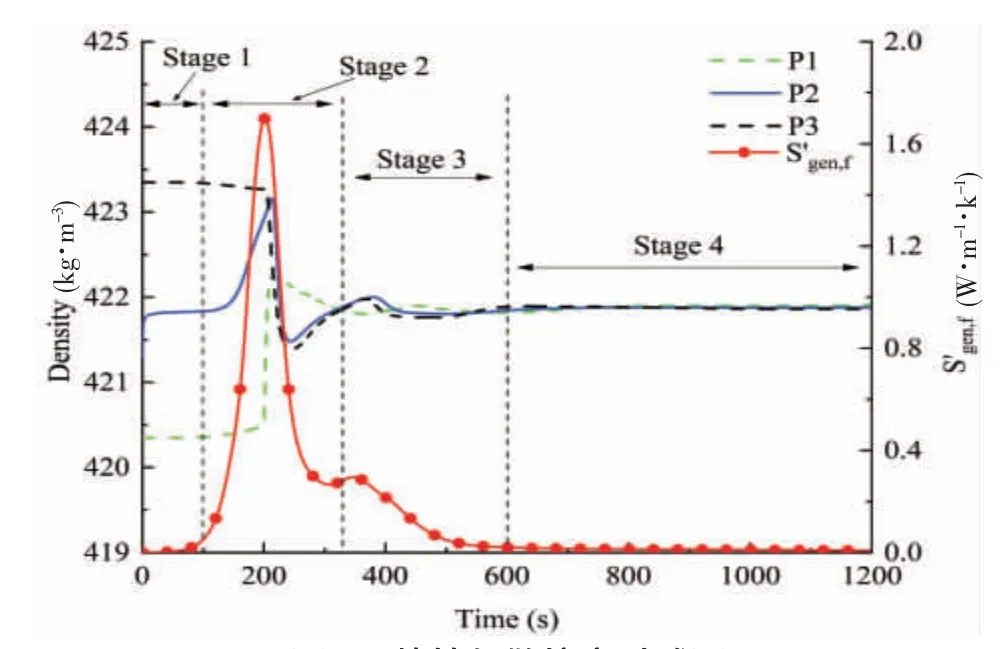
图7 粘性耗散熵产时域图Fig.7 Time history of entropy production by dissipation

通过以上分析表明，传热熵产和粘性耗散熵产能够揭示液舱内LNG 翻滚的演变规律，翻滚行为可以划分为4 个阶段。如图6、7 所示，第一阶段（孕育阶段）：传热熵产第1 次到达波谷，整个阶段表明初期相界面扩散，但未发生界面失稳行为，因此该阶段粘性耗散熵产处于较低水平。第二阶段（翻滚阶段）：传热熵产值从波谷到熵产值趋近于零表明在该阶段界面失稳域内液体发生充分混合，因此该阶段内粘性耗散熵产快速到达峰值并回落。第三阶段（平复阶段）：该阶段主要特征是粘性耗散熵产趋向于零，表明整个域内仍存在着一定强度的对流行为。第四阶段（稳定阶段）：该阶段域内LNG 混合完成，传热熵产和粘性耗散熵产趋近于零。

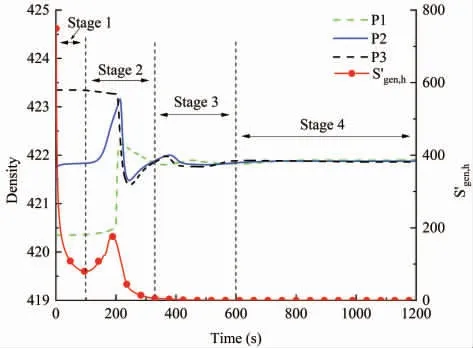
图6 传热熵产时域图Fig.6 Time history of entropy production by heat transfer

2.2 密度差对LNG 翻滚过程的影响

对于60% H 载液率的薄膜型LNG 储罐，两液相分层高度相同。通过熵产分析研究了不同密度差对LNG 翻滚的影响。初始密度差设置为0.5、1、2、3、4、5、6、7、8、9 kg·m-3。图8、9 为不同初始密度差下液舱内传热熵产和粘性耗散熵产时域图。

从整体上看，随着层间密度差的增大，粘性耗散熵产与传热熵产到达峰值点的时刻越早。表明，层间密度差越大，分界面越不稳定，翻滚时间越早。图8 表明，层间密度差增大，翻滚阶段时间减少，主要原因在于，层间密度差的增大使分界面的失稳加速。图9 表明，粘性耗散熵产峰值点随着密度差的增大而提高，表明密度差的增大，使液舱内的翻滚强度提高。

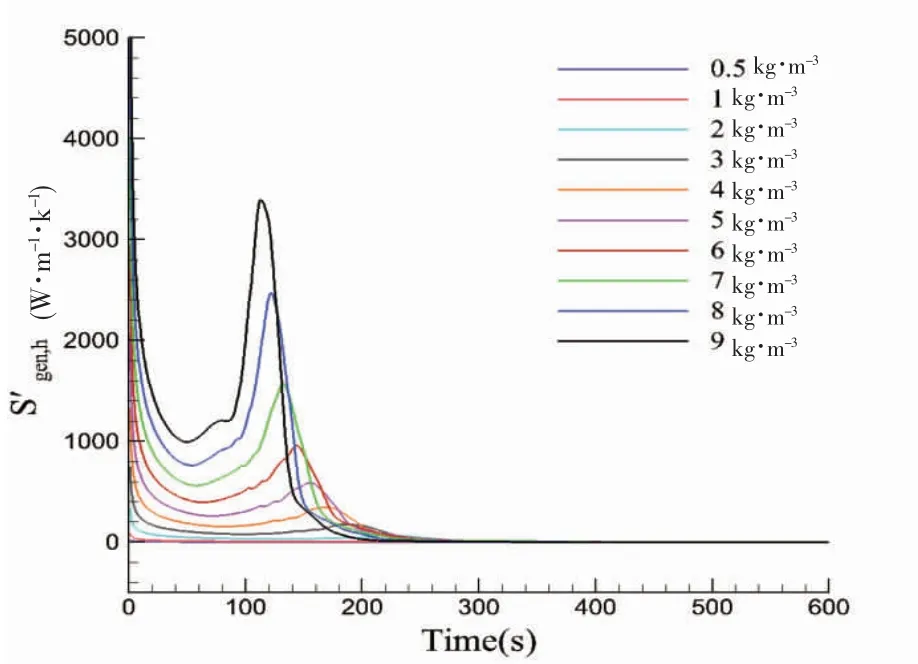
图8 不同密度差下传热熵产时域图Fig.8 Time history of entropy production by heat transfer under different initial density difference

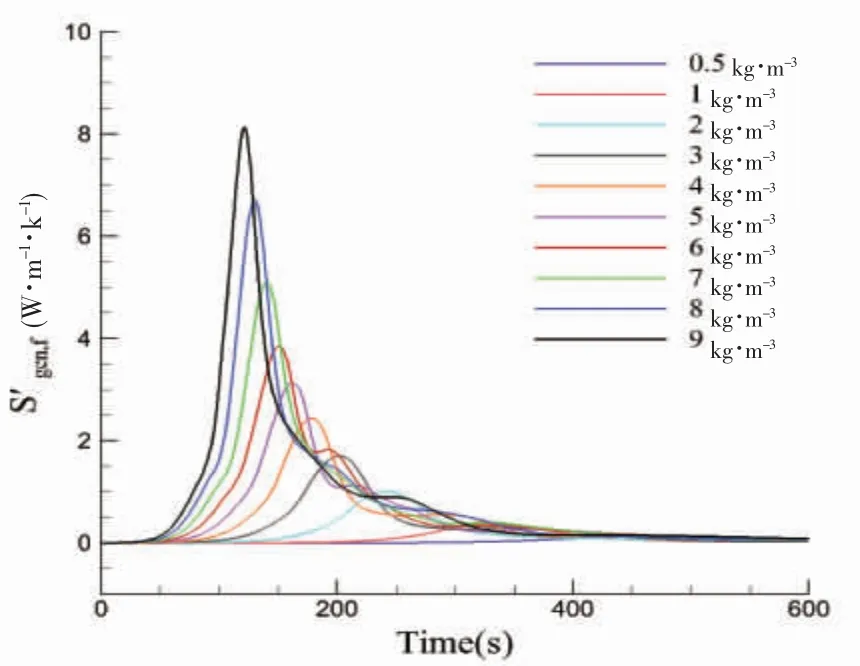
图9 不同密度差下粘性耗散熵产时域图Fig.9 Time history of entropy production by dissipation under different initial densitydifference

为了分析密度差对LNG 翻滚的影响，结合上文分析，设定了平均粘性耗散熵产公式来衡量整个翻滚阶段液舱内LNG 的混合强度。

按照平均粘性耗散熵产公式得出不同初始密度差下平均粘性耗散熵产值，如图10 所示。当初始密度差小于1 kg·m-3，平均粘性耗散熵产波动幅度不大，这意味着这两种工况下LNG 翻滚是相对平稳的。当初始密度差大于1 kg·m-3，平均粘性耗散熵产迅速增加，这意味着液舱将面临较为危险的LNG 翻滚工况。

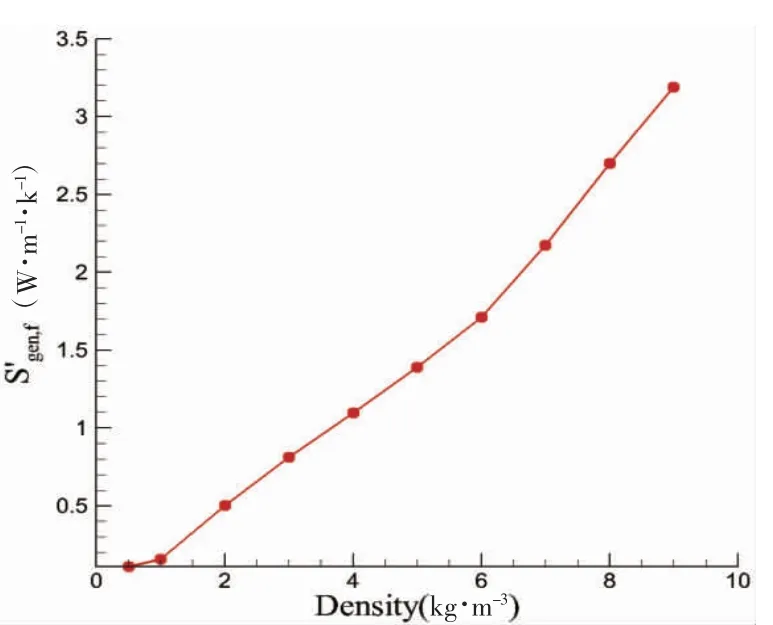
图10 不同初始密度差下平均粘性耗散熵产Fig.10 average entropy production by dissipation under different initial density difference

由此可得，60%H 的LNG 液舱的翻滚临界密度差为1 kg·m-3。

2.3 不同载液率下LNG 翻滚临界密度差研究

在两液相分层高度相同的情况下，结合熵产分析研究了30%H与90%H 两种载液工况下液舱内LNG 翻滚情况。图11～14 分别为30%H 与90%H 载液工况下传热熵产与粘性耗散熵产时域图。

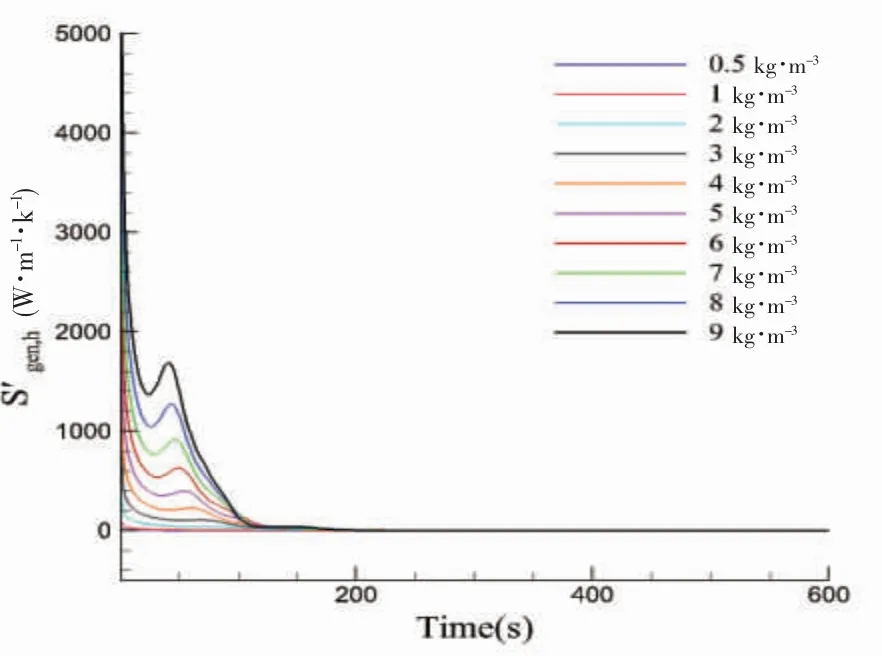
图11 30% H 载液率传热熵产时域图Fig.11 Time history of entropy production by heat transfer under 30% H filling rate

对比上文60% H 载液率下的传热熵产与粘性耗散熵产时域图，可以看出在30% H 载液率下，LNG 开始翻滚的时间最早。表明LNG 存量越小时，LNG 分界面越容易失稳。60% H 与90% H载液率下，粘性耗散熵产与传热熵产峰值相似，原因在于容积大小不再是限制湍流发展的原因。

按照平均粘性耗散熵产公式处理出不同载液率下平均粘性耗散熵产数据，如图15、16 所示。

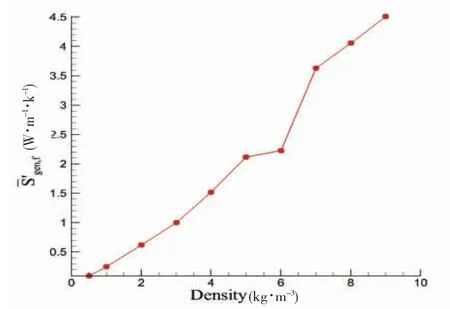
图15 90% H 载液率下平均粘性耗散熵产图Fig.15 average entropy production by dissipation under 90% H filling rate

图14、15 表明，对于30% H 载液率下LNG 翻滚的临界密度差是1 kg·m-3，对于90% H 载液率下LNG 翻滚的临界密度差是6 kg·m-3。以上结果表明，分层高度的增加，使界面的稳定性提高，有助于降低LNG 翻滚的发生。

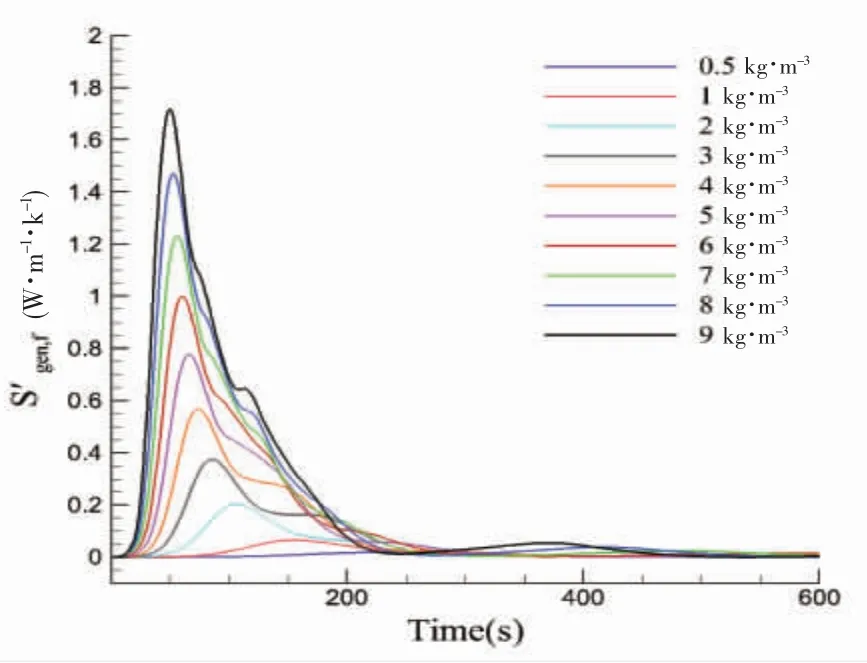
图12 30% H 载液率粘性耗散熵产时域图Fig.12 Time history of entropy production by dissipation under 30% H filling rate

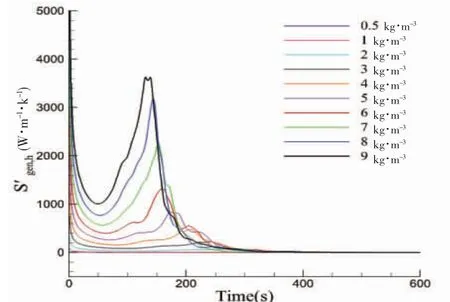
图13 90% H 载液率传热熵产时域图Fig.13 Time history of entropy production by heat transfer under 90% H filling rate

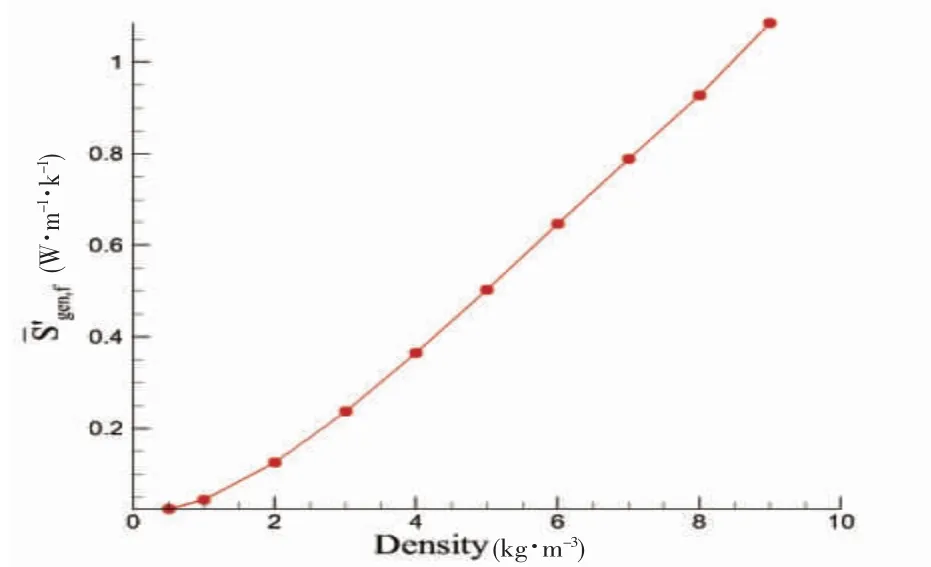
图14 30% H 载液率下平均粘性耗散熵产图Fig.14 average entropy production by dissipation under 30% H filling rate

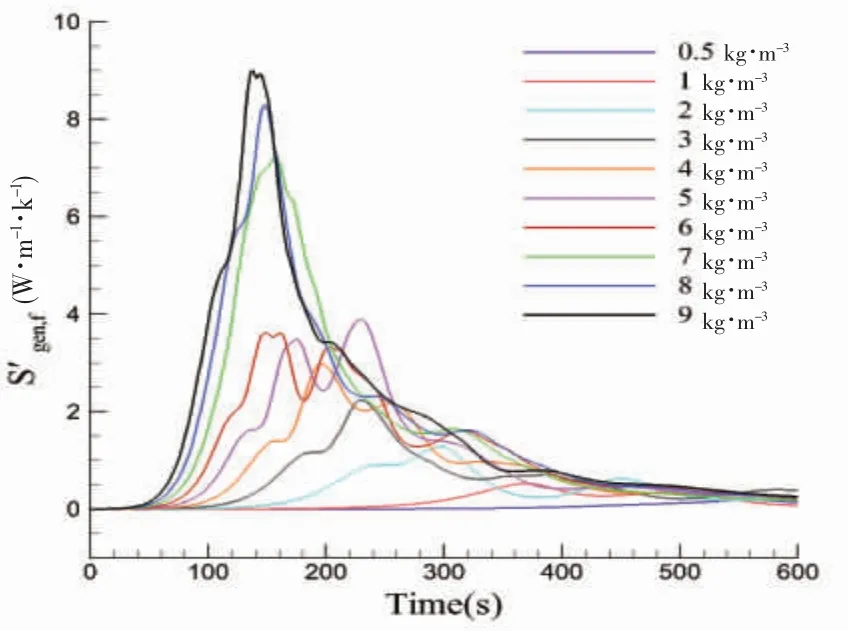
图14 90% H 载液率粘性耗散熵产时域图Fig.14 Time history of entropy production by dissipation under 90% H filling rate

3 结论

本文通过结合熵产分析方法研究了LNG 翻滚过程，以LNG 液舱为研究对象，探究LNG 翻滚过程中液舱内部传热与流动过程的耦合机制，结论总结如下：

（1）通过分析传热熵产和粘性耗散熵产揭示了液舱内LNG 翻滚的演变规律，将LNG 翻滚行为划分为四个阶段：孕育阶段、翻滚阶段、平复阶段、稳定阶段。

（2）不同初始密度差下LNG 翻滚强度不同，相同载液率下，初始密度差越大，翻滚越迅速、越剧烈。

（3）结合熵产理论，定义了平均粘性耗散熵产来描述LNG 翻滚强度。

（4）30% H、60% H、90% H 载液率下临界密度差分别为1、1、6 kg·m-3，提高载液率有助于预防LNG翻滚的发生。