网片出水条件下波高和水深对其水动力特性的影响

杨 熙，刘 灿，潘 昀，冯德军，施圣铃，桂福坤

(1.浙江海洋大学船舶与海运学院，浙江舟山 316022；2.国家海洋设施养殖工程技术研究中心，浙江舟山 316022)

海洋围网养殖工程一般可依托于外侧海岛进行一面或多面围拦，养殖鱼类、贝类等水产经济动物，是新近发展起来并极具应用前景的一种生态养殖模式。近些年随着新材料、新工程工艺、海洋环境适应能力等的快速发展，新的围网养殖工程结构型式也不断出现[1-3]。因此，以提高养殖水产的产量和质量为目的，研究围网养殖工程的水动力安全特性以及研发适用于围网养殖的养殖装备和高效养殖技术，成为大型围网养殖工程设计和研发的前沿问题[3-4]。

以时间和水域空间为主线，围网养殖的发展主要分为两个阶段：第一阶段，由20 世纪20 年代日本的河流拦网养殖到20 世纪50 年代中国湖泊、滩涂围栏养殖，一般在滩涂3～5 m 的浅水区域进行养殖；第二阶段，由2008 年我国出现的海洋围网养殖到2012 年成功投入运营的养殖水域面积大、工程结构安全性能高、运营管理高效的大面积海洋围网养殖工程，养殖水深达到10～15 m 以上。以水产养殖业及海岸工程技术的发展为主线，由早期的竹筏围网逐渐发展成为采用HDPE 管道和桩网结构(钢管桩、预制桩、金属网、柔性网)围成多种形状(方形、多边形、圆形)的单体围网或组合式围网，同时结合连岸工程、防护工程、运输工程、综合管理平台，正努力向机械化、智能化、休闲渔业产业化的方向发展。从已获得的经济效益可以得出，海洋围网养殖工程为海洋养殖提出了崭新的发展方向和技术理论。近年来，随着人们对水产养殖业养殖品质和养殖效益的提高，助推了养殖模式和养殖工程技术的发展，海洋生态围网养殖应运而生。相比滩涂围栏养殖和港湾围网养殖，生态围网养殖在工程结构型式上出现多样化，养殖水体和养殖水域面积越来越大(养殖水体达3×104m3)[5]。围网养殖工程的安全是养殖生产成败的关键，研发新型的围网养殖工程结构首要是提高养殖工程的抗风浪性能和适应复杂的海洋动力环境。

围网养殖工程水平尺度为百米级至千米级，垂直尺度为十米级，主要由网衣系统、网衣支撑系统、浮力和锚泊系统、底部防逃逸系统等部分构成，各系统构件的几何尺寸又在几毫米至几十米之间，材料差异性较大，所以目前对整体围网养殖工程的安全评估的研究较少，往往针对围网养殖工程的各个系统或者重要构成单元(比如桩网结构[6-7]、浮体[8-9]与锚泊[10])进行研究。陈天华等[11-13]采用集中质量点法数值模拟了波浪和水流作用下桩柱间网片不同部位的运动及受力分布特性，从网片的网线张力分布、结节偏移和系缚点受力3 个角度出发，分析了波高、波向、网片尺寸、固定方式和纲绳因素对桩柱式围网网片水动力特性的影响。深究上述研究发现，围网网片均在完全淹没(始终在波谷波面以下)条件下所得出的结论，而波浪对桩柱式围网养殖工程网片水动力特性在出水条件下和完全淹没条件下既有相似之处，亦有差别。因此，在原有采用集中质量点法建立围网养殖工程网片波浪水动力模型的基础上添加网片出水判断模块，深入探讨网片网结的最大偏移量和网线的最大拉力大小和位置受波浪高度和水深变化的影响规律。实际围网养殖工程网片垂直高度为固定值，在不同的波浪要素条件下，网片出水(高于波峰波面)为常态，因此出水条件下探讨波浪对网片水动力的影响非常有意义。

1 数值模拟方法

主要使用集中质量点法计算和模拟桩柱式围网养殖工程网片在波浪作用下的受力和运动。网片主要由网线和网结构成，网片除自身重力外，波浪作用下还受到波浪力和相邻网线的拉力。网片的波浪力根据莫里森波浪力公式计算，其中网线概化成圆柱杆件，网结视为球体。相邻网线的拉力根据相邻两网结的空间位置，概化成弹簧，使用胡克定律进行计算。具体数值模拟方法均已经发表在文献[11-13]中，所以本节内容仅描述围网网片出水条件下波浪理论和网片受力计算的处理方法以及网片结构尺寸的不同之处。

1.1 波浪理论

波浪的水质点速度和水质点加速度与文献[11-13]中的方法保持一致，使用线性波理论，统一波浪的波陡(H/L)为0.05，波浪周期根据弥散方程计算。与之不同的是在计算任意网片集中点位置(x，y，z)的水质点速度和水质点加速度时，首先根据相同时刻的波面线(式(1))进行判断是否出水，再对z 进行修正，如式(2)所示把zd 作为z 的修正位置进行计算。计算修正后的zd 位置的波浪水质点参数更符合出水条件下实际特点。

式(1)和式(2)中以静水面位置为x 轴，垂直向上为z 轴，规定波浪沿y 正方向传播。η 为水面变化，a 为波浪振幅，k 为波数，ω 为圆频率，d 为水深，zd 为修正后的位置坐标。

网片出水条件的判断方法为相同时刻网片质量集中点的z 坐标与波面线η 的关系：如果z 大于η，水质点速度和加速度均为0；如果z 小于或等于η，水质点速度和加速度使用式(2)中zd 的值进行计算。

1.2 网片波浪力计算

假定网片是由有限的无质量弹簧连接的集中质量点所构成，通过计算集中质量点在波浪和边界条件作用下的位移，获得网片的形状[11-13]。模型的集中质量点设于每个网目目脚的两端，每个集中质量点包含网目的1 个网结和2个目脚，如图1 所示，其中任意集中点4 根网线的拉力沿顺时针方向依次命名为f1～f4。

图1 网片集中质量点模型及网线拉力示意图Fig.1 Model of lumped mass point of net and schematic diagram of thread tension

运动网衣受到的波浪力可根据莫里森方程计算，需要使用相对水质点速度[6]，如式(3)。假定网目的结节为圆球，其水动力系数在运动方向上是恒定的；把目脚看作为圆柱形杆件，笛卡尔坐标系下取3 个方向的水动力系数，详细见表1。在目脚上建立局部坐标系，计算当波浪入射方向与网线夹角时目脚的波浪力。

式中VR为水质点相对速度；Vwater为波浪的水质点速度；V0为网片集中点的运动速度。针对式(3)需要特别指出的是，当网片质量集中点的z 坐标大于波面线η 的时，Vwater=0，但在某同一时刻V0并非为0。所以，网片出水条件判断后，VR也应根据z 坐标与波面线η 的关系进行判断是否强制为0。

1.3 网片几何参数

根据已建设的桩柱式围网养殖工程，概化出了如图2 所示的网片作为主要研究对象，网片所有网线上、左、右所有网目系缚在水平桩柱和垂直桩柱上，水平尺寸为5 m，垂直高度为12 m，静水深为10 m，即有2 m 的网衣露出水面。网目的缩节系数为水平缩结系数0.66，垂直缩结系数0.75。考虑计算效率，数值模型中采用网目群化方法[14]将相邻64 个网目合并为一个等效大网目。表1 中所列的模型计算参数与文献[11-13]相同，计算结果与相应物理模型试验结果验证良好。

图2 围网养殖网片数值计算模型Fig.2 Numerical model for the net of pile-column type net enclosure aquaculture engineering

表1 网片几何和模型计算参数Tab.1 Net model setting parameters

1.4 模型计算组次

针对波浪的基本要素和围网网片的出水特点，设计了波高组和水深组分别探讨波高和水深对网片水动力特性的影响，具体工况见表2。所列工况中仅考虑了网片与波向夹角为90°的情况，因为网片正面遭受波浪作用的破坏强度最大，并且以网线中线为对称轴，网片两侧的波浪水动力特性相互对称，所以不再考虑网片与波向夹角对网片水动力特性的影响。其中，每组工况均模拟计算30 s，网片运动在1 个波浪周期内达到稳定，因此结果分析数据选取后15 s 的稳定值。

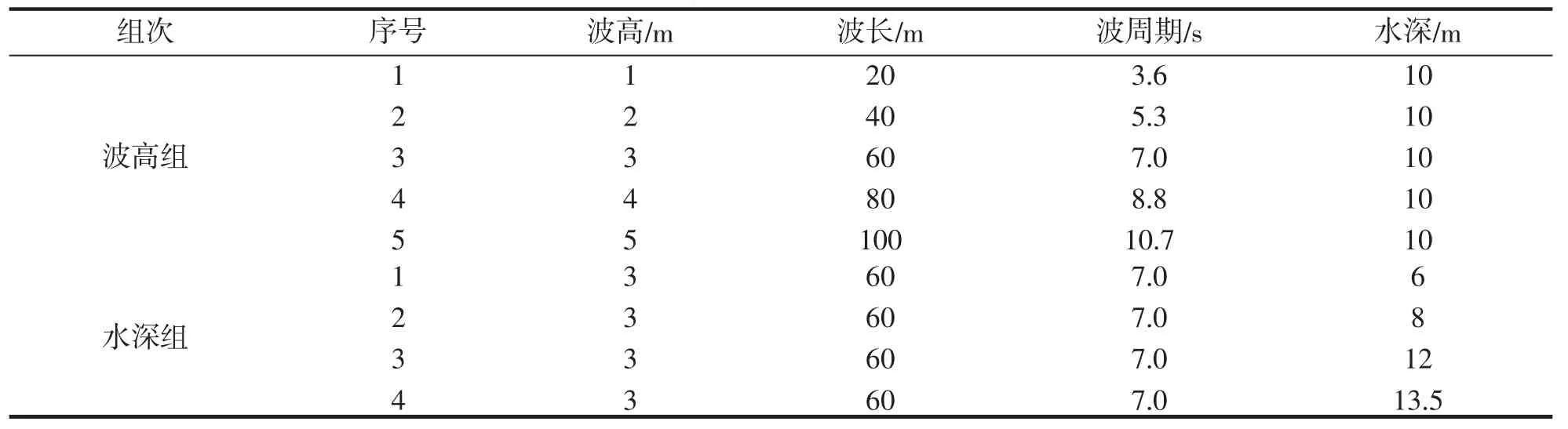
表2 模拟工况Tab.2 Simulation conditions

2 波浪对网片水动力特性的影响

网片由网线和网结构成，因此从网线的运动偏移和网线拉力，即微观细节上分析波浪高度对出水条件下网片水动力特性的影响。如表2 所计算组次所示，波高和水深是影响网结偏移和网线拉力分布影响的主要因素。

2.1 波高对网片偏移量及网线拉力分布的影响

由于波浪90°正面入射作用与围网网片上，而网片所有的结点系缚固定在垂直桩柱和水平桩柱及海底，所以如图2 所示，j=13 列网结伴随波浪运动的偏移量应是最大值。对应表2 中的波高组波浪条件，图3为j=13 列所有网片网结在1 个波浪周期（具体周期见表2）内的运动轨迹。可以得出，网片在出水条件下，负偏移值即为波谷时扫掠过的轨迹，与波峰时的正偏移值并不对称；与不出水条件下结论一致，网片的运动偏移量以及扫掠轨迹的大小均与波高成正比。从图3(6)可以看出，最大偏移量在波浪传播方向(波峰)和反方向(波谷)上的值并不相等，反而反方向上的偏移量略大。

图3 不同波高波浪作用下网片最大偏移量位置处(j=13)15 s 内运动轨迹及最大偏移量变化Fig.3 Motion trajectory within 15 s (j=13) at the position of maximum motion displacement of the net under wave action of different wave heights,and change of maximum motion displacement

讨论波浪作用下网线的最大拉力分布的位置与最大拉力值同样重要，由于网线的拉力与网结(集中点)的空间位置有关，也就是在网片运动偏移量达到最大时，网线拉力达到最大。所以首先讨论网片最大偏移量以及相应发生的时刻就显得十分重要，通过判断和记录图1 中所有波高组次发生网片最大偏移量所对应的时刻，然后分别比较所有网结f1～f4(图1 所示任意结点顺时针方向命名)的大小，分波浪传播正方向和反方向寻找到最大的f1～f4 的大小及z 方向位置。通过分析结果发现，最大网线拉力的位置的f1 和f4的值基本相等，f2 和f3 的值基本相等，说明网线拉力是按照f1-f4-f1-f4-f1……和f2-f3-f2-f3-f2……传递于各个结点，这与文献[11-13]所得结论一致。因此，图4(1)仅分正、负偏移方向f1 和f2 进行了z 方向位置展示。可以得出：波峰时，随着波高的增大，最大f1、f4 和f2、f3 的位置在静水面上方且受波高的影响较小；波谷时，随着波高的增大，最大f1、f4 和f2、f3 的位置在静水面下方且受波高的影响较大，最大f2、f3 的位置比最大f1、f4 底2～4 m。图4(2)中最大网线拉力值随着波高的变化与以往的研究并无较大差异。

2.2 水深对网片偏移量及网线拉力分布的影响

不同水深和相同波高(H=3 m)作用下，同样j=13 列网结伴随波浪运动的偏移量是最大值。对应表2 中的水深组波浪条件，图4 为j=13 列所有网结在1 个波浪周期（7s）内的运动轨迹。可以得出，网片在出水条件下，负偏移值即波谷时扫掠过的轨迹面积随着水深的增大而增大，当水深较小时(如图5 中(1)和(2)、(3))可以看出左侧的网结轨迹在出水条件下出现杂乱的抖动，这与水下的网线瞬时的张力有关。从图5(6)可以看出，最大偏移量在波浪传播方向(波峰)和反方向(波谷)上的值并不相等，反而在大水深时反方向的偏移量略大。

图5 不同水深波浪(H=3 m)作用下网片最大偏移量位置处(j=13)15 s 内运动轨迹及最大偏移量变化Fig.5 Motion trajectory within 15 s (j=13) at the position of maximum motion displacement of the net under wave action of different water depths,and change of maximum motion displacement

图4 最大网线拉力分布及受波高影响Fig.4 The maximum thread tension distribution and the effect of wave heights

同理，通过判断和记录图1 中所有水深组次发生网片最大偏移量所对应的时刻，然后分别比较所有网结f1～f4(图1 所示任意结点顺时针方向命名)的大小，分波浪传播正方向和反方向寻找到最大的f1～f4的大小及z 方向位置。与波高组工况结果一致，最大网线拉力位置的f1 和f4 的值基本相等，f2 和f3 的值基本相等。因此，图6(1)仅分正、负偏移方向f1 和f2 进行了z 方向位置展示。可以得出：水深为10 m 时，不仅正方向最大网线拉力的位置达到最高，而且也发生转变（随水深增加而降低）；负方向最大网线拉力的位置受水深变化的影响较小。图6(2)给出了最大网线拉力值随着水深的变化的情况，最大网线拉力随着水深的增大而减小，但当网片顶端与静水面齐平时（即水深为12 m），最大网线拉力将发生转变，稍微增大。

图6 最大网线拉力分布及受水深影响(H=3 m)Fig.6 The maximum thread tension distribution and the effect of water depths（H=3 m）

3 讨论

波浪对桩柱式围网养殖工程网片水动力特性在出水条件下和完全淹没(始终在波谷波面以下)条件下网片网结的最大偏移量和网线的最大拉力大小和位置受波浪高度和水深变化的影响规律既有相似之处，亦有差别。实际的围网养殖工程网片垂直高度为固定值，在不同的波浪要素条件下，网片出水(高于波峰波面)为常态，因此出水条件下探讨波浪对网片水动力的影响非常有意义。陈天华等[11-13]在完全淹没条件下得出，波高对网线最大拉力和结点最大偏移都有显著的影响，网线最大张力和结节最大偏移随波高的增大迅速增加。由图3(6)和图4(2)明显看出，该结论与出水条件下一致。不同之处是最大偏移量在波浪传播方向(波峰)和反方向(波谷)上的值并不相等，反而反方向上的偏移量略大。深究网片结点上所有网线的拉力大小和分布，发现图1 中网线拉力f1 和f4 的值基本相等，f2 和f3 的值基本相等，也就是说明网线拉力是按照对角形式传递于各个结点。波峰时，随着波高的增大，最大f1、f4 和f2、f3 的位置在静水面上方且受波高的影响较小；波谷时，随着波高的增大，最大f1、f4 和f2、f3 的位置在静水面下方且受波高的影响较大，最大f2、f3 的位置比最大f1、f4 底2～4 m。这些规律与完成淹没条件下网线最大张力发生在网片上端两侧，结节最大偏移发生在网片上部，位置都不受波高影响等有很大不同。

为了进一步阐明出水条件下网片的波浪水动力特性，论文还对比分析了定波高(H=3 m)，多组水深条件下网片网结偏移量和最大网线拉力的分布变化。研究发现，存在2 个特殊的水深导致网片最大网线拉力位置和大小发生明显变化：（1）当网片顶端与波峰波面较为接近时，网结上4 根网线的拉力极值垂向分布差异较大，此时网片受到全部波浪的作用，网片的受力所以发生转变；（2）网片顶端与静水面齐平时，网片只受到波谷至静水面部分波浪的作用，所以最大网线拉力并不再随着水深的增加而减小，相当于网片下沉受到了水体的保护。

4 结论

对出水条件下桩柱式围网养殖工程网片波浪水动力特性进行了数值模拟研究，分析探讨了不同波高和水深下的网片偏移量、网线拉力分布及最大网线拉力，得到以下基本结论：

(1)网片最大偏移量在波浪传播方向(波峰时刻)和反方向(波谷时刻)数值不相等，反方向上的偏移量略大，而淹没条件下(网片垂直高度低于波谷波面)接近对称分布。

(2)网片网线拉力沿对角形式传递于相邻结点。随着波高的增大，最大网线拉力在波峰时刻的位置在静水面上方且受波高的影响较小，而在波谷时刻的位置在静水面下方且受波高的影响较大。

(3)当网片的垂向高度与波峰波面较为接近时，网片网线的拉力极值垂向分布差异较大，当网片的垂直高度与波峰波面齐平时，最大网线拉力并不再随着水深的增加而减小。

由以上主要结论可知，实际应用中，由于网结上4 根网线最大拉力分布并不在同一位置，任一网线达到极限拉力值都将导致网片破裂，需要更多关注设计波高条件下波峰至波谷范围内网片的加固设计和防破坏措施。在相同的波高条件下，仍需要考虑低潮位时期围网工程的安全。