融合阈值寻优的卷积神经网络在图像标注中的应用

曹建芳，赵爱迪，张自邦

（1.太原科技大学计算机科学与技术学院，太原 030024；2.忻州师范学院计算机系，山西忻州 034000）

（∗通信作者电子邮箱kcxdj122@126.com）

0 引言

随着网络技术的发展以及多媒体设备的日益普及，网络上的图像数据正以指数级增长。面对大量的无标签图像的产生，如何检索、管理和组织这些图像成为一个亟待解决的问题［1］。很多专家学者提出了对图像进行添加标签，即图像标注，进而可以合理有效地管理这些图像数据。

目前图像自动标注的方法有两类：一是基于传统机器学习的方法，如：吴伟等［2］提出的基于改进的支持向量机（Support Vector Machine，SVM）的方法，通过建立多个分类器，形成以距离大小为判别依据的支持向量机多分类模型，此外还为每个分类器引入了权重系数。臧淼等［3］提出的基于距离约束稀疏/组稀疏编码的两种特征选择算法，利用学习到的特征权值寻找K最近邻图像实现图像标注。杨晓玲等［4］提出的基于多标签判别字典学习的图像自动标注，在字典学习中加入多标签学习，将两者融合在一起进行图像的多标签标注。张华忠等［5］对决策树C4.5 进行改进，提出了修正矩阵（Correction Matrix-C4.5，CMC4.5），并将其应用在图像标注领域。二是基于深度学习［6-7］的方法，如：Hinton［8］提出了利用深度神经网络，从训练集中有效地训练特征。柯逍等［9］提出了融合深度特征和语义邻域的自动图像标注，利用卷积神经网络（Convolutional Neural Network，CNN）提取特征，构建视觉和语义均相近的近邻图像集，通过计算距离给标签排序进而进行标注。周铭柯等［10］针对图像标注数据不平衡的问题，提出了基于数据均衡的增进式深度自动图像标注，利用堆叠自编码器（Stacked Auto-Encoder，SAE）的自动图像标注算法，加强训练中低频标签的编码器，同时加强了该模型的鲁棒性，提升了模型的稳定性。张蕾等［11］提出了一种融合卷积神经网络与主题模型的图像标注，首先改进了卷积神经网络的损失函数，其次利用狄利克雷模型对训练集的标签数据进行建模，通过图像的高层视觉特征和图像的标签数据的对应关系构建多分类器。黄冬梅等［12］提出了一种融合多特征的深度学习图像自动标注方法，赋予每个图像视觉特征不同的权重并将它们组合成词包，根据输入输出变量优化深度信念网络。黎健成等［1］提出了基于卷积神经网络的多标签图像自动标注，利用了多标签损失排名函数，完成了多标签数据的训练与测试。

传统的方法在取得一些进展的同时也存在着一些问题：在图像特征提取的过程中，人工提取图像特征就会不可避免地出现人为主观错误，导致图像信息提取错误，实验精确度差。而深度神经网络模型在图像标签领域取得了一定的成绩，但是也存在一些不足［13］：首先，深度神经网络是包含多层非线性操作的模型，它具有很强大的表示能力，可以学习很多复杂结构，越复杂的结构越容易导致过拟合［13］。其次，上述深度学习标注模型都是对模型本身进行改进，这些模型在标注过程中只给出预测概率，通过排名确定标注标签，在不知道该图片标签数量的情况下就会出现多标或少标的问题。因此，需要充分考虑每类标签的概率情况，为每一类标签寻找到一个最佳阈值，从而提升标注的准确率。

为了解决上述问题，首先提出在激活层之前添加批标准化层（Batch Normalization，BN），不仅在一定程度上可以防止过拟合，还极大地提升了训练速度，收敛过程也大大加快。其次，提出融合阈值寻优的卷积神经网络的方法。通过搭建一个卷积神经网络学习图像特征，利用反向传播算法训练模型得到模型参数［13］；模型再对测试集进行预测得到概率矩阵，通过对概率矩阵进行阈值寻优，为每类标签找到一个最佳阈值。

1 卷积神经网络

卷积神经网络（CNN）［14］是一种前馈神经网络，其本质是一个多层感知机。20 世纪60 年代，Hubel 等［15］通过对猫脑皮层中用于局部敏感和方向选择的神经元的研究而提出了感受野这个概念。1980 年，日本科学家Fukushima［16］提出了一个包含卷积层和池化层的神经网络。在现有研究的基础上，1998 年LeCun 等［17］提出了LeNet-5，将反向传播（Back Propagation，BP）算法应用在了神经网络的训练上，初步形成了当代卷积神经网络。而卷积神经网络得到较大的发展是在Krizhevsky等［14］提出的AlexNet在ImageNet图像识别大赛中将错误率从25%降低到了15%。从此，卷积神经网络得到了学者的广泛关注，结构越来越复杂，表达能力越来越强。CNN采用的局部连接和权值共享的方式：一方面丢弃了部分神经元，减少了过拟合的风险；另一方面不同神经元之间的参数共享减少了权值的数量，使得网络更加易于优化。卷积神经网络的主要结构包括输入层、卷积层、池化层、全连接层以及最后的输出层，通过叠加卷积层和池化层来加深网络层数。卷积神经网络通过卷积层的卷积运算自动提取图像的特征，减小了传统方法中人工提取特征导致信息丢失的错误率，在计算机视觉领域取得了很大的成功。基于卷积神经网络的优点，本文提出融合阈值寻优的卷积神经网络模型。卷积层是卷积神经网络的核心部分，是对卷积神经网络中上一层的输出进行特征提取，该过程会使用多个卷积核进行卷积运算，最终得到多个特征图（feature map）。卷积运算公式［18］如式（1）：

其中：表示为第i层第j个卷积核输出的特征图；Mj表示为第i-1 层的所有特征图；表示为第i层的一个卷积核；表示为第i层中的特征对应的偏置；f()表示函数运算；“*”表示卷积操作。为了尽可能多地获得特征，在卷积的过程中会使用多个卷积核，该过程不可避免地会导致信息冗余。为了降低特征维度，在卷积之后会采取池化操作，目前常用的池化操作有最大值池化、平均池化等。经过池化过程之后，特征图的维度就会降低，池化过程如图1所示。

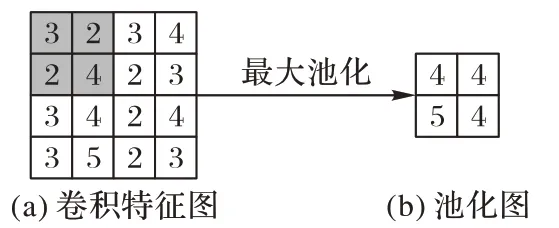
图1 池化窗口为2×2的池化过程Fig.1 Pooling process with 2×2 pooling window

该过程中，可以看到最大值池化就是在每一个池化窗口中选择一个最大值的输出，图1（b）就是经过最大池化输出的池化层的特征图。本文采用的是最大值池化，可以很好地保留图像的纹理信息。

损失函数是衡量输出的预测值和真实值之间的差距程度。对于二分类问题，通常在输出层采用Sigmoid激活函数计算预测标签的值，由于Sigmoid函数的特殊性在训练的过程中会导致梯度越来越小，于是使用交叉熵损失函数（cross entropy loss function）替代均方差（Mean Square Error，MSE）损失函数。而对于本文的多标签标注问题，转化为了在每个标签上的二分类问题，输出层同样采用Sigmoid 函数计算预测值，每一个标签都是独立分布的，互不影响于是本文使用了二分类交叉熵损失函数（binary_cross entropy loss function）也叫作二元交叉熵损失函数，如式（2）所示：

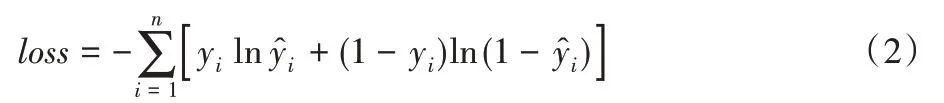
其中：n是标签数量；yi是i类标签的真实值；是i类标签的预测值；loss是单个样本的损失函数。

2 融合阈值寻优的卷积神经网络模型

本文采用的卷积神经网络结构如图2 所示，输入层是同样规格大小的图像，大小都是100×100×3，3 代表着R、G、B 三个通道。中间的处理层包括8层卷积，4层池化以及在每个激活函数之前都增加了BN 层加快了收敛速度，其中8层卷积操作采用的卷积核都是经典的3×3 的大小，卷积核的个数分别为32、32、64、64、128、128、256、256；池化层采用的均是最大池化，池化窗口均是2×2 大小的；为防止过拟合进行了Dropout 操作，概率设置为0.5；之后进行了Flatten 操作，把数据压扁平准备全连接。最后输出层中，两个全连接层，使用的节点分别是512 个和5 个。整个网络结构中只有最后输出层的激活函数采用的是Sigmoid激活函数，其余激活函数均采用线性整流函数（Rectified Linear Unit，ReLU）。优化器采用的是随机梯度下降（Stochastic Gradient Descent，SGD），学习率的初始值为0.01，学习率自动更新下降。

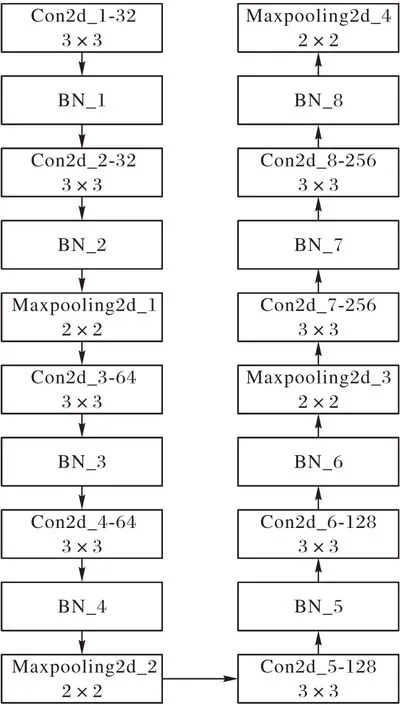
图2 本文使用的卷积神经网络结构Fig.2 Structure of used CNN

2.1 基于BN操作的收敛速度的加快

深度神经网络在训练的过程中因为隐层神经元的输入分布不稳定，导致网络不能学习稳定的规律，同时随着网络层数的加深，激活输入值的分布逐渐偏移，越来越靠近非线性函数的极限饱和区，导致反向传播时梯度越来越小直至消失。在进行新的批次数据训练时，网络就要重新学习这批数据的特征，这就导致随着网络层数加深，梯度越来越小，训练越来越困难，收敛越来越慢。于是，提出了BN［19］这个概念，把每一个隐层神经元的激活分布固定下来，把上一层神经元的输出都标准化（正态分布），通过这一步可以把激活输入值拉回到非线性区域的线性区域，加大了导数值，增强了梯度，同时为了提高网络的表达能力，再进行一次变换，之后再输入到下一层神经元中。这样就可以避免因网络层数的加深，导致训练数据越来越偏的问题。同时固定了网络的各层输入数据的分布，使得激活输入值都落在对输入比较敏感的区域，这样一点小的变化就会导致损失函数较大的变化，加大了梯度，能大幅提高收敛速度，解决了在反向传播的过程中底层网络梯度消失的问题。BN［19］的具体操作如下所示：

其中：x是某个隐层神经元没有经过变换之前的激活值；m是批处理中的实例数；γ和β是网络训练过程中不断迭代学习到的参数，类似于权重和偏置；μB是批处理训练中m个实例的均值；是批处理训练中m个实例的方差；是某个神经元对应的原始激活x减去批处理中m个实例的均值再除以方差进行的变换；ε是误差；yi是规范化后的网络响应。

经过上述步骤1）～3）可以把某个神经元的激活x形成一个正态分布，向非线性区域的线性区域靠近，增大了导数值和反向传播的流动性，加快了收敛速度。但是由于把激活值拉到了线性区域，导致网络的表达能力下降，于是通过训练学习到的两个参数γ和β，再一次对变换后的激活进行反变换也就是步骤4），提高了网络的表达能力。

2.2 融合阈值寻优设置最佳阈值

通过卷积神经网络模型对测试集中的图片进行测试，得到一个概率数组，数组元素是每张图片的每类标签的预测概率，是否分配这个标签给这张图片，对此需要为每类标签设置一个最佳阈值。阈值寻优的过程如下：

步骤1 将模型预测的测试集标签概率放入数组out。

步骤2 定义一个数组a。

步骤3 为阈值threshold设置范围［0.1，0.8］，步长为0.1。

步骤4 初始化最佳阈值best_threshold［0 0 0 0 0］。

步骤5 读出out中的第i列元素（i从1 开始），代表的是测试集中所有图片的第i个标签，记为y_prob。

步骤6 取出threshold中的第j个值（j从1 开始），与y_ prob中的元素依次进行比较，如果大于等于j就设置为1，否则为0，记为y_pred。

步骤7 把预测标签y_ pred与真实标签y_test［：，i］进行马斯修运算，把运算结果赋给a。

步骤8 重复步骤6～7，直到把j遍历完。

步骤9 把a中最大数所在位置的索引赋给index。

步骤10 在threshold中取出index这个索引位置所对应的阈值赋给best_threshold［i］，作为第i类标签的阈值。

步骤11 重复步骤5～10，直到把所有标签遍历完。

2.3 多标签图像标注框架

首先，训练数据集对卷积神经网络进行训练得到标注模型，其次，模型再对测试数据集进行预测得到预测概率，对预测概率进行上述的阈值寻优过程得到最佳阈值，最后，把待标注图像载入到标注模型和最佳阈值中完成标注过程。其基本框架如图3所示。

图4 是传统的图像自动标注框架，通过图3 和图4 的对比，可以看到本文的方法增加了阈值寻优的过程，通过阈值寻优设置最佳阈值可以解决固定标签数目带来的多标或少标的问题。

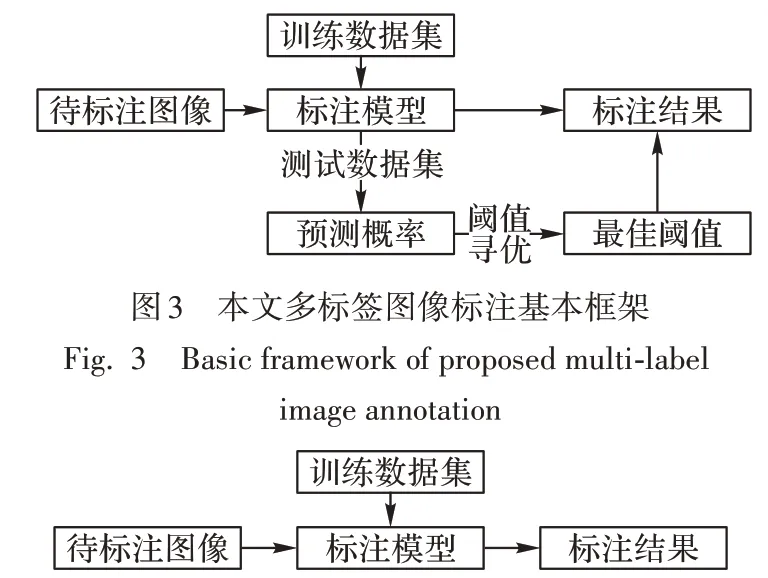
图4 传统图像自动标注框架Fig.4 Traditional image automatic annotation framework

3 实验与结果分析

3.1 实验设计

3.1.1 实验环境

代码的实现基于Intel Xeon W-2102 CPU @2.9 GHz 的处理器、NVIDIA GeForce RTX 2080Ti 的显卡以及16 GB 的内存的硬件环境，使用Windows 10 操作系统和Keras 库搭建软件环境，实验平台是PyCharm，语言是Python。Keras库是一个公开的深度学习库，可以作为TensorFlow 和Theano 的应用程序接口，是对TensorFlow 和Theano的封装，不必过多地关注底层结构，由于其高度模块化可以快速搭建网络结构，大幅提升开发效率，比TensorFlow更加容易使用。

3.1.2 数据集

本文使用的数据集是来自于南京大学机器学习与数据挖掘研究所提供的关于自然场景的图像库，共有2 000 张图片，由于数据集过小，通过数据增强把数据集增加到8 000张。图片大小不一致，经resize（）函数操作之后，缩放为100×100 大小的，其中训练集包含有6 400 张图片，测试集有1 600 张图片，这些图片共有5 类标注词，分别是desert、mountains、sea、sunset、trees，数据集的详细信息［20］如表1所示。

3.2 评价指标

本文采用多种评价指标，如平均查准率P、平均召回率R以及F1，为了能够更加准确地说明标注的效果，增加了一个新的评价指标完全匹配度（Complete Matching Degree，CMD）。完全匹配度在这里是新提出的一个概念，是指在测试每一张图片时，测试的标注词结果和图片的真实标注词完全一致，既没有遗漏也没有多余标注词，实现了精准标注。作为实验结果的评价标准，平均查准率P、平均召回率R以及平均F1值计算式如下：

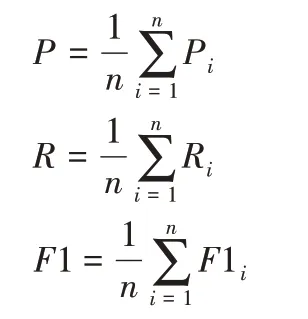
其中：n表示的是标签类别数，本文中等于5，代表5 个标签即5 个标注词；Pi表示的是i类标签的查准率；Ri表示的是i类标签的召回率；F1i表示的是i类标签的F1值。

表1 数据集相关信息Tab.1 Information related to datasets

完全匹配度为：

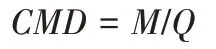
其中：M表示预测标签和真实标签完全一致的图片个数；Q表示测试集大小。

3.3 结果分析

3.3.1 对BN操作的实验验证

为了验证添加BN 层可以加快收敛速度，本文对添加BN层的网络结构和不添加BN层的网络结构进行训练，随着迭代次数的增加，准确率（Accuracy）的变化情况如图5所示。

由于训练时长关系，对不添加BN 层的迭代200 次和添加BN 层的迭代100 次进行实验以说明BN 层的作用。图5 中的（a）、（b）两图的横坐标均是迭代次数（Epoch），纵坐标均是准确率（Accuracy）。如图5（a）所示，在不添加BN 层的情况下准确率达到80%需要迭代大约50 次，在迭代20 次的情况下准确率仅达到了75%。如图5（b）所示，在添加BN 层的情况下准确率达到80%大约仅需要迭代15次，达到75%的准确率大约需要迭代5次，表明BN层可以很好地加快收敛速度。

3.3.2 对最佳阈值的实验验证

为了寻找到最佳阈值，对各组阈值进行了对比实验，表2中的各组阈值是迭代相同次数（Epoch=500）的模型所对应的最佳阈值，通过把各个模型所对应的最佳阈值载入到最优模型中，找出最佳阈值。

从表2 可以看出，新增加的一个评价指标CMD使得实验结果的评价更为严谨和苛刻。首先，整体分析各组阈值的实验结果，发现差距不大，说明训练得到的最优模型效果不错。因此，基本认为这个卷积神经网络模型在本数据集上的多标签图像自动标注问题上没有太大的问题。其次，虽然各组阈值的结果差距不大，但综合考虑到完全匹配度是最高的，因此选择［0.3 0.3 0.2 0.1 0.7］作为最佳阈值，其中CMD在这个实验中达到了64.75%，这再次验证了最佳阈值的有效性。

图5 迭代准确率变化Fig.5 Accuracy variation with iteration

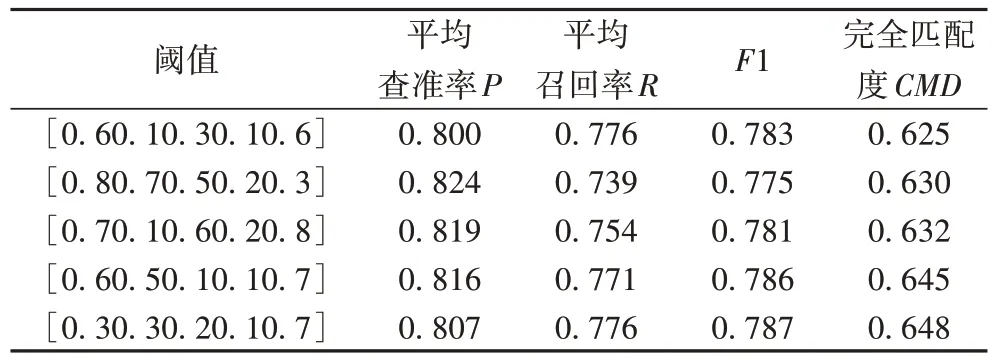
表2 各阈值实验结果Tab.2 Experimental results of various thresholds

3.3.3 与其他图像标注方法对比

为了验证本文提出的融合阈值寻优的卷积神经网络（CNN with THreshold OPtimization，CNN-THOP）模型在图像自动标注上的有效性，将与传统方法基于排名的支持向量机（Ranking Support Vector Machine，Rank-SVM）法［21］和ADTBoost.MH （Multiclass，multi-label version of boostingalternating decision trees based on Hamming loss）［22］以及近些年来常用的深度学习方法卷积神经网络回归（CNN Regression，CNN-R）［23］和采用MSE 误差函数的CNN（CNN using Mean Square Error function，CNN-MSE）［18］进行比较，实验结果如表3所示。

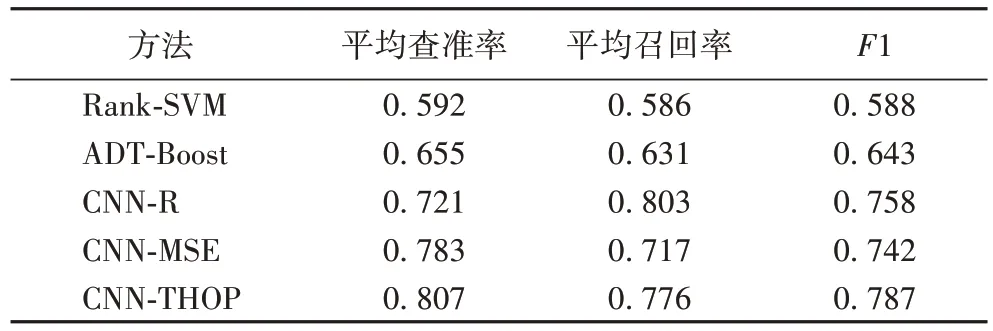
表3 各图像标注方法的实验结果Tab.3 Experimental results of different image annotation methods

从表3 中可以看出，本文提出的方法融合阈值寻优的卷积神经网络（CNN-THOP）模型和传统方法Rank-SVM 相比，平均查准率上提升了约20 个百分点，平均召回率较ADT-Boost提升了约14 个百分点，表明卷积神经网络在特征提取方面要优于传统方法。通过和卷积神经网络相比，平均查准率较CNN-R 提高了约8 个百分点，平均召回率较CNN-MSE 将近提升6 个百分点，表明最佳阈值的设置可以更灵活地标注标签，解决了固定标签数目带来的问题，这再次验证了本文方法的有效性。

3.4 模型实际标注效果

图6中列出测试图片，表4中给出各实验方法自动标注的实际效果，其中选取传统方法Rank-SVM 和深度学习方法CNN-MSE与本文方法预测标签进行对比。

从表4 中可以看出，本文方法比其他方法在图像自动标注方面更加有效，对于大多数图像都可以完全正确地标注标签，不会出现多标或少标的问题，解决了其他方法因固定标签数目所带来的问题。最后一幅图像的标注虽然比真实标注少了一个，原因可能是因为该类图像太少，模型没有很好地学习到这个特征。对于CNN-MSE的标注结果，可以看出因固定标签数目所带来的多标或少标的问题比较多。总体来看，本文方法在图像自动标注方面是有效的。

图6 测试图片Fig.6 Test images

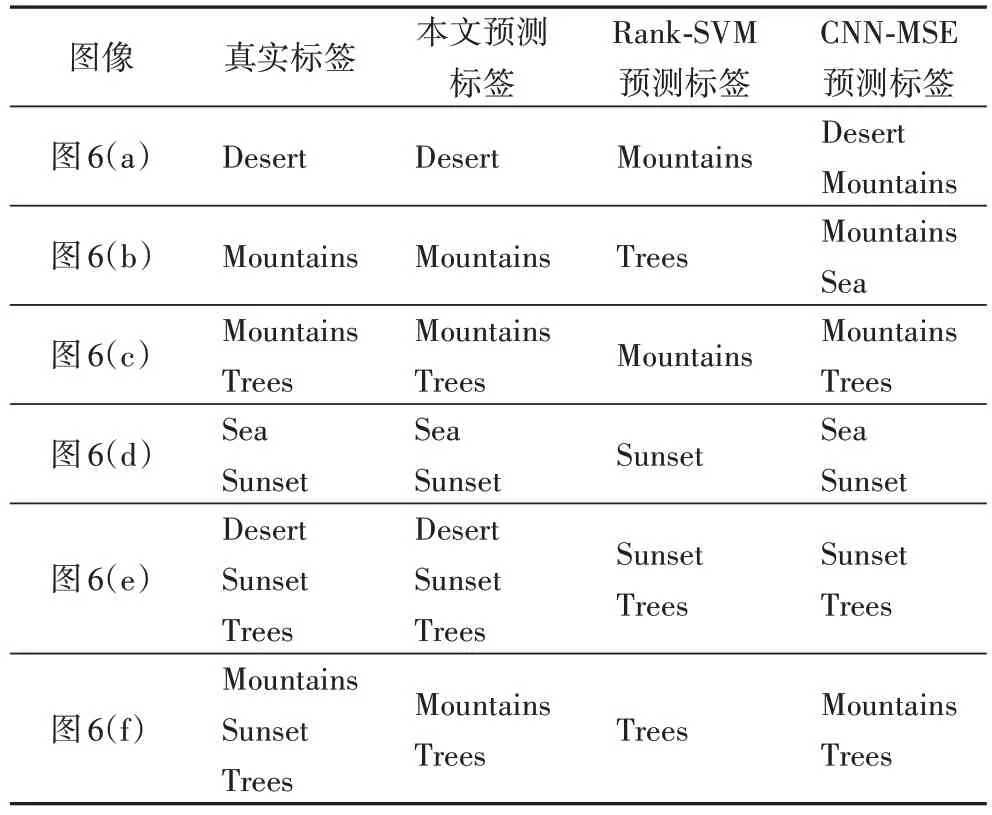
表4 各实验方法图像标注结果对比Tab.4 Comparison of image annotation results of different methods

4 结语

针对多标签图像标注过程中固定标注数量、根据排名函数标注标签的问题，本文增加了阈值寻优的过程，最佳阈值的设置使得标注更加合理有效。融合阈值寻优的卷积神经网络模型在测试过程中平均查准率、平均召回率和F1值都有了很大的提高，完全匹配度上也有较好的表现，达到了64.75%。而BN层的添加更好地加快了收敛，表明本文方法能够有效地标注图像。

本文的不足之处：采用的数据集使用的人比较少，在对比方面存在着一定的局限性。下一步工作准备在两个方面进行展开：1）融合多个数据集使得训练的模型更加具有普适性；2）在特征提取方面把人工提取特征和卷积操作结合在一起，更加完善特征提取以免遗漏。