多维时间序列异常检测算法综述
胡 珉,白 雪*,徐 伟,吴秉键
(1.上海大学悉尼工商学院,上海 201800;2.上海大学—上海城建建筑产业化研究中心,上海 200072)
(∗通信作者电子邮箱18225515145@163.com)
0 引言
多维时间序列是指具有多个维度的有序数据集,相比单维时间序列,多维时间序列的时间复杂度和空间复杂度更高、无效和干扰信息更加严重,同时各维度之间也存在着更为复杂的关联情况,使得对于多维时间序列的研究难度呈几何级数增长。
对于时间序列的数据挖掘起始于20 世纪90 年代并且发展迅速,文献[1]认为其挖掘内容涵盖了时间序列的相似性查询、时序模式挖掘、时间序列分类和聚类、时间序列异常检测等领域。
本文研究的对象是多维时间序列异常检测,它作为数据挖掘的重要研究领域,是各行各业尤其是大型工程项目密切关注的内容。例如,在互联网领域,需要通过监测和分析网络数据的实时状态发现异常情况,及时采取措施最终保障信息安全;在大型基础设施的施工和运维过程中,需要通过分析各类传感器的数据信息,及时发现风险隐患,实时报警并辅助管理人员采取有效措施,减少项目经济损失,保障人员安全等。
然而,多维时间序列异常检测算法异常困难:一是维数升高带来的“维数灾难”;二是随着时间增长,数据量激增带来的“信息膨胀”。这不仅增加了算法计算量,提高时间复杂度,加重处理数据的负担,不利于实时检测;而且复杂的关联性容易干扰数据的真实结构,增加数据分析的难度,导致错误的分析处理结果[2]。为解决以上问题,学者们采用“维数约简”和“时间序列模式表示”两种思路处理原始数据,在保留原始数据的基本结构情况下,去除细节干扰,从横向和纵向两个角度对数据集规模进行压缩,从而提高数据分析效率和数据挖掘的准确性。
下面分别对文中的关键名词进行定义。
定义1异常。
关于异常的定义,目前还没有统一标准,当前认可度较高的定义:异常指的是数据集合中明显与众不同的数据,这些数据是由不同的机制产生的,而非随机偏差[3]。异常可以分为点异常、模式异常和序列异常三种形式,本文中的异常发现主要指对点异常和序列异常的发现。
定义2维数约简。
给定D维数据集X={x1,x2,…,xN|xi∈RD},设d维数据集Y={y1,y2,…,yN|yi∈Rd},D>d。若存在函数F(xi),1 ≤i≤N使得X→Y,构成映射RD→Rd,那么就称Y为X维数约简后的数据集。因此,维数约简的实质就是求函数F(xi)。
定义3时间序列模式表示。
给定含m个样本的多维时间序列数据集X={x1,x2,…,xm|xi∈RN},m>1,通过相关算法将原始的多维时间序列数据集压缩为含n(m≫n,n≥1)个样本的多维时间序列数据集Y,其中Y={y1,y2,…,yn|yi∈RN},时间序列模式表示,可理解为时间维度上的维数约简。
目前国内外研究多维时间序列异常检测有两种思路:第一种思路是将多维时间序列进行横向分割,转换为多个单维时间序列,利用单维时间序列领域的算法发现异常模式;第二种思路是对多维时间序列进行纵向分段,通过相关算法研究发现异常点和异常序列。从整体逻辑顺序来看,首先需要对原始数据集进行预处理,然后将预处理后的数据集按照这两种不同的方法进行异常检测,具体如图1所示。
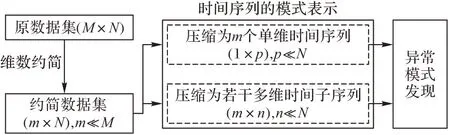
图1 多维时间序列异常检测算法技术路线Fig.1 Technical routes of multidimensional time series anomaly detection algorithm
本文主要围绕多维时间序列异常检测技术路线进行阐述,通过对维数约简、时间序列模式表示和异常发现三大热点领域进行分析整理,总结和分析目前多维时间序列异常检测领域的研究现状和研究趋势。
1 维数约简
避免“维数灾难”最有效的方法是进行维数约简,维度约简分为选维和降维两种类别[4]。选维指的是从原始的高维空间中根据异常检测的目的直接选取相关维度,文献[5]认为主要的选维方法包括:顺序选维算法、遗传算法、基于分形的选维算法和机器学习的选维方法等。相比选维方法,降维算法是指从一个维度空间映射到另一个维度空间的过程,降维后原始时间序列维度的含义和对应数值均会发生变化。
由于降维算法是目前维数约简理论研究的主要方向,而且应用较为广泛,因此本文主要介绍降维算法,无特别强调,后文中维数约简方法指的是降维算法,其主流算法可以分为线性和非线性两种类别,如图2所示。
1.1 研究现状
1.1.1 线性降维的主流算法
线性降维算法是维数约简领域最早提出的一类算法,此类算法的核心是找到各维度之间存在的线性关系,然后对重复表达的信息进行删除,从而达到降维的目的。目前其主流的算法包括主成分分析(Principal Component Analysis,PCA)、线性判别分析(Linear Discriminant Analysis,LDA)等。
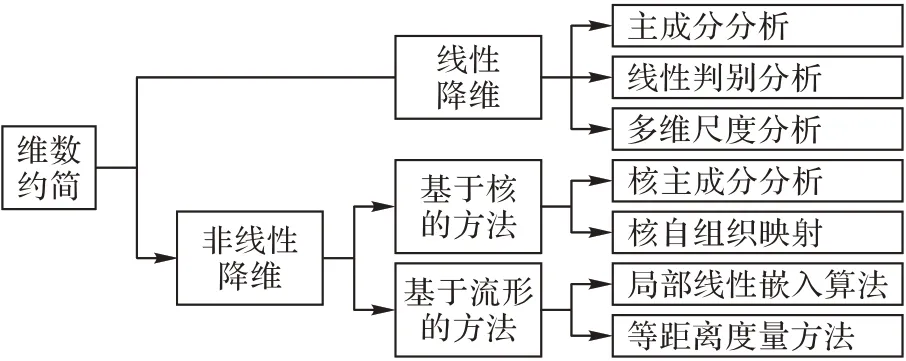
图2 维数约简主流算法分类Fig.2 Classification of main algorithms for dimension reduction
线性降维领域中的经典算法是PCA,该算法是一种无监督的统计分析方法,其计算简单,应用广泛。文献[6-9]的结果显示对多维数据集进行PCA 降维要明显优于不降维得到的结果。但是文献[10-11]将PCA 算法应用于多维时间序列异常检测时,发现其检测效果不是很理想,它们认为PCA 算法在降维过程中只是反映了空间相关性却没有考虑时间的相关性,同时该算法对异常值、参数值和校正集比较敏感。
为此,文献[10]提出了一种基于Galerkin 的KL 扩展算法(KL Expansion,KLE)计算方法,并将其应用于流量异常检测中,实验结果显示该算法能够考虑时间的相关性,其异常检测结果有比较显著的改善。文献[12]提出基于小波变换的全网络异常检测算法MSPCA(Multiscale Principal Component Analysis),该算法考虑了多维时间序列的时空特性,经验证其降维结果要优于PCA 算法和KLE 算法。文献[13]通过对比在工业加工和化学计量领域发展更为成熟的基于PCA 的多元统计过程控制(Multivariate Statistical Process Control,MSPC)与传统PCA 的差异,提出多元统计网络监测(Multivariate Statistical Network Monitoring,MSNM),从而将MSPC 引入到网络应用领域,实验结果证明,利用MSNM 可以有效避免PCA 存在的缺陷。为降低PCA 的对异常值的敏感程度,文献[14]将稳健主成分分析(Robust Principal Component Analysis,RPCA)应用于网络包捕获数据的异常检测,实验发现该算法调整参数较少并且不需要很多的训练数据就能达到较好的检测效果。
1.1.2 非线性降维主流算法
随着数据集规模的激增,学者们发现线性降维算法已经无法描述多维数据集各维度之间复杂的非线性关系,于是开始逐步研究非线性降维算法。
最初的非线性降维算法是基于已有线性降维算法的改进算法,即基于核的非线性降维算法,比较经典的算法是核主成分分析(Kernel Principal Component Analysis,KPCA),但是这类算法的难点在于难以选择合适的核函数。
流形学习是近年来非线性降维算法领域的热门研究方向,2000 年《Science》刊登了两篇流形学习算法,分别是文献[15]提出的局部线性嵌入(Locally Linear Embedding,LLE)算法和文献[16]提出的等距离度量方法Isomap(Isometric Method),这两篇论文从算法层面验证了高维非线性数据空间内确实存在非线性流行结构,标志着学术界开始对流形学习的研究。该研究认为多维数据集主要呈现的是非线性关系,利用线性降维算法很难对其进行准确的描述,比如经典的瑞士卷数据集,如图3所示。A点和B点的实际距离并非实线所对应的线性长度,而是虚线所对应的曲线距离,使用线性降维算法明显不符合此类数据的真实结构。

图3 瑞士卷数据集Fig.3 Swiss volume dataset
流形学习算法的关键在于从高维数据集中找到潜在的低维流形结构,从而实现降维的目的,其算法主要包括Isomap、LLE、多维尺度(Multidimensional Scaling,MDS)分析等。从文献[16-19]整理中发现目前流形学习算法主要应用于图像识别等领域;同时在多维时间序列的应用研究也有一定的成果[20-25]。目前,应用于时间序列的主流算法有Isomap、LLE 及其改进算法。
KPCA 算法是基于PCA 的改进算法,其算法的原理是通过核函数将非线性数据转换为线性数据,然后利用PCA 算法从而实现非线性降维,该算法原理简单,在矩阵比较稀疏的情况下其计算复杂度不高,是非线性降维的经典算法之一。文献[24]通过对水文时间序列的预测模型算法对比,发现“KPCA+SVM”的预测结果要明显优于“PCA+SVM”的结果,说明了在该类数据集中,KPCA 降维效果要优于PCA。但文献[26]发现KPCA 算法虽然在性能上要优于PCA,但是在实际应用中该算法对子集划分和核函数的选取比较敏感。文献[27]将KPCA 和其他基于机器学习分类器的方法应用于时间序列的异常检测,通过实验结果发现KPCA 的检测结果要优于独立成分分析(Independent Component Analysis,ICA)、PCA等传统的方法。文献[28]提出基于部分核主成分分析(Partial Kernel Principal Component Analysis,PKPCA)算法研究故障检测与隔离问题,然后应用于工业燃气轮机传感器实验数据中,结果显示该算法能够有效地检测和隔离故障。文献[29]将KPCA 应用于无人机传感器数据异常检测领域,实验结果发现,该算法的监测效果良好。
Isomap 算法是一种非迭代的全局优化算法,其核心思想是将MDS 算法中的欧氏距离转换为测地距离。文献[16]将该算法应用在图像识别领域,实验结果表明该算法的降维结果要优于PCA 和MDS。但是,传统的Isomap 算法计算复杂度很高,拓扑结构不够稳定,对于低维结构是非凸子集的高维数据集有效性不强[30]。为了降低算法的复杂度,文献[31]提出地标-等距离度量方法L-Isomap(Landmark Isometric Method),该算法首先利用MDS 随机选取若干地标映射到低维空间,之后通过距离计算确定非地标点在低维空间的相对位置,该算法能够大大提高计算效率但是其降维结果对地表点十分敏感。为此,文献[30]提出了两种自适应的地标点选取机制,分别基于贪婪策略和图论中的图顶点染色思想,经实验表明这两种机制均能起到比较理想的降维结果。文献[25]认为基于全局的降维算法(例如:PCA、Isomap 等)没有充分考虑多维数据集的时间相关性,因此提出时空等值线图STIsomap(Spatio-Temporal extension to Isometric method)改变局部邻域图中的原始权重,以强调时间相关点之间的相似性,作者将ST-Isomap算法应用于人体运动和机器人遥控操作数据,实验结果证明了该算法的有效性。文献[32]结合基因序列自身的特点,提出了基于Isomap 的一种变种即双有界树连接等值映射方法(double-bounded tree connected Isometric method,dbt-Isomap)[32],在对基因时间序列进行维数约简的实验中结果良好。文献[33]提出针对噪声时间序列数据的Isomap 样本外扩展方法,实验结果表明,与其他时间感知嵌入算法相比,提出的样本外扩展方法在存在各种噪声和伪影的情况下,能够提供更健壮、更准确的有序图像数据嵌入。文献[21]将Isomap 算法应用到股票的多维时间序列中,实验结果验证了Isomap算法的合理性和可行性。
LLE[15]假设数据在较小的局部范围内是线性的,因此在局部范围内采用欧氏距离代替测地距离,通过保证局部最优来实现降维,因此该算法相较于Isomap 能够有效地降低计算量。文献[22]将LLE 算法应用到金融多维时间序列的聚类中,实验结果表明利用LLE 算法进行降维得到的结果要优于使用PCA 得到的效果,但是该算法较难确定嵌入维数和近邻个数的参数。文献[23]将LLE 算法进行改进,提出基于概率的有监督局部线性嵌入(Supervised Locally Linear Embedding based on Probability,PSLLE)和基于概率的快速监督局部线性嵌入(Quick Supervised Locally Linear Embedding based on Probability,PQSLLE),并应用于煤矿瓦斯浓度时间序列异常监测数据,取得较好的效果。文献[34]为提高LLE 算法的准确度,提出了带监督的LLE(Supervised LLE,SLLE)算法并应用传感器的故障识别中,实验结果发现利用SLLE算法的降维效果要明显优于LLE、PCA 和MDS 算法。文献[35]认为LLE算法只是对简单的数据结构降维比较有效,而在噪声、大曲率和稀疏采样条件下,它并不能准确地处理邻域的选择。因此,作者提出了一种改进的加权局部线性嵌入算法(improved Weighted Local Linear Embedding Algorithm,WLE-LLE),该算法利用拉普拉斯特征映射重构降维目标函数,实现结果发现其能够有效地表示非线性数据的流形结构,分类识别率要比LLE 算法提高2%~8%。文献[36]将LLE 算法应用于非线性、非平稳的脑电图数据中,通过提取经离散小波变换得到的逼近分量的非线性特征,并结合神经网络进行分类,实验结果显示该方法聚类分布明显、分类效果好而且稳定性强,证明了脑电信号处理中流形学习的可行性。
1.2 研究趋势
随着多维时间序列数据规模的激增,传统的线性降维算法已经很难在准确、完整地保留其数据特征的前提下实现维数约简,非线性降维算法尤其是流形学习将成为该领域未来重要的研究方向。
根据非线性降维算法已有的理论成果,本文将该领域的研究趋势总结为以下几个方面:
1)将已有理论成果与实际应用场景相结合,进一步确定算法的特点和适用范围。目前文中涉及的诸多理论算法都只是在特定的实验数据集或者人工数据集上进行测试,算法在解决具有实际背景的多维时间序列时的可行性还需要进一步的分析和验证,这是将理论成果转换为实际应用的重要环节。
2)算法优化。整理发现,目前在该领域算法的缺陷主要表现在:时间相关性研究不够深入、参数设置较多、计算复杂度较高、鲁棒性不强等方面,在之后的算法研究中,可以从以上的一个或多个方面对算法进行优化。
3)结合机器学习或深度学习实现维数约简[37]。这些算法具有自学习能力,理论上非常适合于对海量时间序列的处理,因此可以将此类算法引入该领域解决时间序列的降维问题。
2 时间序列模式表示
时间序列模式表示是从时间角度对原始数据进行抽象和概括的特征表示方法,是对时间序列的重新描述。该方法能够在保证原始数据基本形态和信息的基础上实现数据压缩。
目前在该领域的理论研究中,针对单维时间序列异常检测的研究成果相对成熟,因此许多文献会将多维时间序列转换为多个单维时间序列,利用单维时间序列研究成果解决多维时间序列异常检测问题。该领域的算法根据文献[38]可以分为精确表示和近似表示,如图4所示。

图4 时间序列模式表示主流算法分类Fig.4 Mainstream algorithms of pattern representation of time series
2.1 研究现状
在时间序列压缩方式中,主流的方法有:抽样表示法、分段线性表示法(Piecewise Linear Representation,PLR)、符号化表示法(Symbolic Aggregate Approximation,SAX)、离散傅里叶变换(Discrete Fourier Transform,DFT)等,下面分别对这几类主流算法的研究现状进行分析和介绍。
2.1.1 抽样表示法
抽样表示法[39]是时间序列最简单的表示方法,该算法的原理简单,即按比例抽取样本点,同时易于实现,适用于实际工程中的多维时间序列的实时压缩,但是其采样步长很难确定,当该参数取值过大时,会使样本变形导致表示不准确。
针对该问题,Keogh 等[40]提出分段聚合近似(Piecewise Aggregate Approximation,PAA),该方法在抽样表示方法的基础上使用平均值来表示每个分段对应的数据点集,减小了因抽样导致的时序数据的变形程度,但是其准确度以及步长的确定仍然是需要进一步完善的问题。为防止该算法丢失时间序列的重要模式,同时保证其存在良好的下界约束,Hung等[41]提出了分段线性聚合近似(Piecewise Linear Aggregate Approximation,PLAA)算法,该算法结合均值和斜率两个方面,能够弥补PAA 算法的不足。文献[42]针对PAA 步长问题提出基于混合层次聚类的PAA(hybrid Hierarchical Clustering-PAA,hybrid HC-PAA)算法,在基于振动特征的工业燃气轮机故障检测和基于超声回波信号的生物特征识别两个数据集的应用中具有良好的表现。为了解决PAA 算法数据特征丢失的问题,文献[43]提出分段聚合模式表示(Piecewise Aggregate Pattern Representations,PAPR),并将其应用于心电图数据和视频监控数据的异常检测,实验结果显示,与基于PAA 的方法相比,基于该方法的异常检测算法具有更高的鲁棒性和更精确的异常检测能力。文献[44]针对PAA 存在的问题给出了两种解决方式:第一种方法是根据平均值将每一段划分为两部分,并分别使用数值平均值来表示趋势,该方法已被证明满足下界约束,从而保证不会产生漏报;第二种方法使用二进制字符串来记录时间序列的趋势变化,实验表明该方法要优于之前提出的PAA算法。
2.1.2 分段线性表示法
Pavlidis 等[45]提出PLR,该算法是指采用首尾相邻的一系列线段来近似表示时间序列,其难点在于如何进行样本分段,确定分段数目和分段点。
针对此问题,文献[46]提出基于PAA 的PLR 算法,将时间序列等宽分割,然后用均值代替该子时间段。该方法简单直观,能够提高索引的效率,可以应用于多维时间序列压缩。文献[47]提出了基于重要点的分段方法,文中通过选取局部极值点来实现数据的压缩。文献[48]提出基于特征点的PLR算法,将影响时间序列形态的最大的点作为特征点进行线性分段,该算法虽然在选择特征点的过程中对噪声的处理结果较好,但无法及时捕获单调序列中的变化转折点,不能有效发现短暂变化的尖峰子序列。之后,文献[1]提出基于时态边缘算子的分段线性(piecewise linear representation based on Temporal Edge Operators,TEO)表示方法,算法考虑到时间序列的非平稳性和相关性特点,选择局部范围内的边缘幅度极值点作为边缘点进行时间子序列的划分,算法具有较强适应性,能够应用于不同的数据特征环境。文献[49]提出一种基于插值边缘算子的时间序列分段线性表示(piecewise linear representation based on Interpolation Edge Operators,IEO)方法,可以有效压缩数据,并且对噪声和数据是否陡峭并不敏感,在异常检测中能够具有更好的表现效果。文献[50]认为大部分的PLR 算法具有动态增量实时更新的优点,于是提出基于信息熵的PLR_IE(Piecewise Linear Representation based on Information Entropy)算法,利用序列中熵的大小比例来确定序列中重要点的数量分布情况,从而线性拟合出初始曲线,实验结果表明,与现有的距离计算分析查找特征点相比,该算法能够更准确地提取序列重要特征,保留了序列整体性。文献[51]为解决时间序列的分割问题,提出基于压缩比的分段线性表示法。首先找出时间序列中的所有极值点,然后根据压缩比例选取符合要求的极值点作为序列分割点,该算法原理简单,同时不需要设置复杂的阈值参数,但是该算法的鲁棒性不强,存在拟合误差,只适用于单维时间序列的离线分割。为减小PLR 算法的拟合误差,文献[52]提出基于重要点的线性分段表示法(Piecewise Linear Representation based on Important Data Point,PLR-IDP),该重要点通过计算单点拟合误差和分段拟合误差来确定,结果显示该算法能够在保留数据主要特征的情况下,实现较低的单点、局部和全局拟合误差。为减少参数设置,提高算法的拟合效果和鲁棒性,文献[53]提出基于时间序列重要点的分段(Piecewise Linear Representation based on the Important Point of the Time Series,PLR-TSIP)算法,该算法从整体拟合误差角度确定每段的优先级,然后在段内按照最大最小值点进行进一步划分,实验结果表明,该算法的拟合度较高,但是其计算效率还需要进一步提高。
2.1.3 符号化表示方法
时间序列的符号化表示方法中最常用的就是文献[54]提出的SAX 算法,该算法是基于PAA 的扩展方法,被认为是该领域最简单同时稳健性最强的处理单维时间序列的算法[55]。由于目前字符串领域的匹配研究比较成熟,因此许多研究者会将时间序列离散化,然后映射到字符空间,利用字符串技术来对时间序列进行研究,但是该方法基于对时间序列的均值描述,其结果比较粗糙容易导致数据失真,同时难以描述时间序列的趋势特征。
Wang等[56]结合SAX、卷积神经网络和集成学习算法提出Pooling SAX-BoP (Pooling SAX Algorithms with BoP Representations),并应用于医学领域并取得了较好的结果,证明了SAX 算法在该领域的可行性。为解决数据失真问题,文献[57]结合SAX 距离与加权趋势距离提出SAX-TD(SAX with the weighted Trend Distance)从而实现了对时间序列更加准确的分类。文献[58]提出基于标准差的SAX(SAX based on Standard Deviation,SAX-SD)改进算法,通过在UCR 数据集的验证,发现该算法与SAX、SAX-TD 算法相比具有更高的压缩比率和更高的效率,同时能够满足下界约束和紧束缚距离,该算法在异常检测中的应用有待进一步研究。文献[59]提出基于滑动窗口的重要转折点的SAX 改进算法FD-SAX(Featurebased Dividing SAX),该算法能够实现在线流式时间序列符号表示,通过各种类型的实验数据对比证明了该算法的优越性。为解决SAX 算法难以描述时间序列趋势特征的问题,文献[60]提出基于趋势的改进SAX 方法(Trend-based SAX,TSAX),通过UCR 时间序列数据集验证了该算法的有效性,但是该算法难以更加精确地刻画趋势的程度,另外其距离值的测量方法不具有普遍性,同时其参数问题也没有得到有效的解决。文献[61]在SAX 方法的基础上进行了改进,提出时间序列的多维符号化表示方法mSAX(multidimensional SAX),该改进算法是从多个维度来描述子序列片段并将其转化特征向量,然后利用离散化方法对各子序列特征向量的各个维度进行符号化生成多维符号向量,结果显示该方法对时间序列的描述和表示更加精准细致。
2.1.4 离散傅里叶变换法
DFT[62]基本思想是在全局范围内将时间序列分解为有限个数的正弦函数和余弦函数的加权和。DFT能够用极少的傅里叶系数来表示时间序列,能够大幅度节省存储空间并且能够保持欧几里得距离不变性,但是它很难刻画时间序列的局部特征。为了克服该缺点,文献[63]提出了短时傅里叶变换(Short-Time Fourier Transform,STFT),即在信号上加一段滑动窗口对信号进行分段取样,将其化为若干个局部平稳信号,但是STFT 的问题是很难确定滑动窗口的大小。离散小波变换(Discrete Wavelet Transform,DWT)可以解决上述问题,它具有多分辨率解析的特点同时包含时域信息和频域信息,能更加有效地提取和分析局部信号,在原始信息的除噪过程中也经常使用该算法[64],在时间序列模式领域已逐渐代替了DFT 和STFT。文献[65]采用Harr 小波变换,实验结果表明采用离散小波变换在相似性查询时结果要优于DFT 表示方法。文献[66]提出将遗传算法、聚类算法和DWT 进行结合,即利用K-means聚类将子序列分组,DWT保证子序列的相同长度,然后利用遗传算法发现分割点,实验结果表明,该方法能在时间序列中找到合适的分割模式。文献[67]提出分别利用LLE和DWT 算法提取运动图像脑电图的特征,然后结合神经网络算法实现更加稳定和有效的分类效果。文献[68]运用DWT算法提取扰动特征,同时提出基于人工蜂群的概率网络(Probabilistic Neural Network based Artificial Bee Colony,PNNABC)算法优化特征选择,从而实现对电能质量扰动的有效分类。
2.2 研究趋势
目前时间序列模式表示领域中对于单维时间序列的算法研究已经相对成熟,因此,对于单维时间序列,未来的研究趋势主要侧重于对已有算法的优化,主要包含以下几个方面:
1)实时性在线扩展能力。目前已有算法大部分只适于对离线数据进行时间维度的数据压缩,对于动态数据的处理主要基于滑动窗口的设置。但是随着数据量的增加和实际应用中对于实时异常检测需求的提高,越来越多的时间序列需要满足在线情况下、有限时间内完成对数据的实时检测,因此,对于该算法的实时性研究具有很大的经济价值。
2)可扩展性。目前已有的算法大部分需要设置较多的参数和阈值,由于不同数据集的特征迥异,对参数的调整和训练将耗费大量的时间,导致算法的可扩展性不强。因此,在今后研究中可以对参数设置进行优化和改进。
相对于单维时间序列模式表示,目前国内外对于多维时间序列模式表示方法理论成果较少[69],处在初步研究阶段。但是随着当代各行各业尤其大型基础设施对全生命周期海量数据实时处理要求的提高,对于该领域的理论研究需求愈加迫切。通过分析发现,目前研究瓶颈在于难以确定多维时间序列的分段规则。因此,在该领域的研究可以从以下几个方向展开:
1)基于已有的单维时间序列模式表示方法提出改进算法使其能够适用于多维时间序列。
2)研究多维时间序列模式表示算法,直接从多维时间序列的角度解决模式表示问题。同时,在算法的研究中要着重考虑算法的实时性、计算复杂度、可扩展性等一个或者多个方面,从而提高算法在实际应用中的可行性。
3 异常模式发现
异常模式发现是多维时间序列异常检测最重要的研究领域之一,目前在该领域的主流算法主要分为以下五类,如图5所示,本章将对这五类算法进行分析整理,并说明该领域的研究趋势。
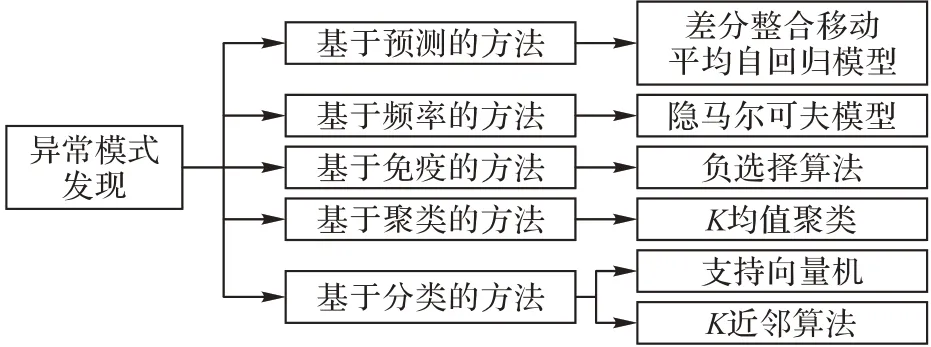
图5 异常模式发现的主流算法Fig.5 Mainstream algorithm of anomaly pattern detection
3.1 基于预测的方法
基于预测的方法是通过预测值与实际值的误差值大小来判断异常位置,代表算法是差分整合移动平均自回归模型(AutoRegressive Integrated Moving Average model,ARIMA)[70],其适用于具有明显季节性或周期性的单维时间序列的短期异常检测。
国内最初将ARIMA 用于气象数据和传染病数据[71-73],由于这些时间序列相对简单,周期性很强并且具有明显的规律,因此其预测值和实际值的误差比较小,在具体的实验数据中表现良好。
目前基于预测的方法逐渐从传统的以ARIMA 模型为核心的线性预测算法发展到“ARIMA+”的组合预测算法。比如:文献[74]提出ARIMA-LSSVM 的混合预测算法,分别对单维犯罪时间序列进行线性和非线性部分建模,实现对精准的犯罪预测,与传统的ARIMA-BP 相比,该混合算法的准确性和稳定性更高,但是此类算法参数设置较多同时其计算复杂度也偏高。文献[75]结合ARIMA、DWT和功能链接人工神经网络(Functional Link Artificial Neural Network,FLANN)对单维金融领域数据进行预测,通过DWT 将原始时间序列分解为线性和非线性部分,然后分别利用ARIMA 和FLANN 算法实现线性和非线性预测,实验结果证明了该算法的有效性。文献[76]将ARIMA 结合SVM 算法应用于单维网络流量的趋势预测,该算法需要对原始数据进行长期观测提取相关特征,然后对各类特征分别建立ARIMA 模型,将实际值与预测值的差值作为偏离度向量,通过不断更新偏离度并结合支持向量机(Support Vector Machine,SVM)算法实现对该网络流量的实时在线预测,实验验证该算法能够有效地预测异常情况。文献[77]提出改进的ARIMA算法M-ARIMA(Modified ARIMA),将该算法应用于由光纤力热参数仪中的压力传感器实时采集的数据集中,经验证该算法具有较高检测率的同时能够自动、实时地实现异常预警。文献[78]提出结合ARIMA、DWT 和RNN 实现对计算机网络流量的预测,其原理与文献[75]基本一致,作者认为该混合方法易于实现并且计算量相对较小,能够显著提高网络服务质量、减少成本。文献[79]基于ARIMABP 的混合算法预测氨气的浓度,通过实验对比,发现该算法在该领域的预测结果要优于BP神经网络或ARIMA模型。
3.2 基于频率的方法
该方法的代表算法是隐马尔可夫模型(Hidden Markov Model,HMM)[80],该模型是关于时序的概率模型,异常检测在HMM 中可以转换为“在给定观测序列O(t),t=1,2,…,T和模型λ=(A,B,π)的前提下,求取P(O|λ)”的问题,该算法解决的是单维时间序列问题,其最显著的特点是要求其观测值是有限个数的离散值,能够实现实时检测。
围绕HMM 有许多实际的应用,文献[81]将HMM 应用到时间序列异常检测中,实验结果验证了该算法的有效性,但是传统的HMM算法在建模过程中时间复杂度过高、样本需求量大并且对状态参数比较敏感。
针对样本需求量大的问题,文献[82]提出基于半监督学习的行为建模与异常检测方法,即通过结合DTW、谱聚类和HMM,建立正常行为和异常行为的模型,从而得到异常行为判断模型,对人的运动行为数据进行分析,实验证明该算法适用于多类样本的情况,能够在较少样本的情况下避免HMM欠学习的问题,具有较高的可靠性,但是该算法时间复杂度仍然较高,不能检测到未知异常,同时对于小样本类型的正常行为检测效果也需要进一步完善。文献[83]提出了一种增量的HMM 学习算法,将训练集切割为若干个规模较小的子集分别进行训练,最后将训练得到的子模型合并为最终的模型,实验显示该方法能够大幅度减少计算时间。孙美凤等[84]提出了基于特征模式的马尔可夫链异常检测模型,该算法能够避免重复性检测,实验显示,该算法简单、实时性强、检测率高、误报率低,但是其对参数设置比较敏感,能够直接影响算法的检测效果。
针对时间复杂度过高同时状态参数敏感的问题,王琼等[85]提出改进的隐马尔可夫模型(Improved HMM,IHMM),为降低算法对阈值参数的敏感性,该算法将训练数据集中发生频率极低的特征序列删除,利用发生频率较高的特征序列建立正常行为轮廓,经实验对比发现,该算法在训练时间、适应性等方面都明显优于HMM模型。
近几年HMM算法开始和机器学习结合来改进预测效果,比如文献[86]提出的将HMM 算法结合自组织神经网络等。同时,该算法已逐步运用到其他领域,比如信用卡欺诈检测[87]、行为识别[88-89]、器械故障检测[90]等。
3.3 基于免疫的算法
负选择算法(Negative Selection Algorithm,NSA)[91]基于生物学中免疫系统的自我-非我识别原理,该算法的基本原理是通过正样本获得能够尽可能覆盖非我空间的检测器集,然后利用检测器对系统的运行状态进行甄别。负选择算法基于大量的正样本进行学习,不需要先验知识,非常适合于异常样本匮乏或者未知故障的检测问题,但是该算法中检测器数目和检测器对非我空间的覆盖两者之间是相互矛盾的,这也成为目前众多学者研究的热点方向。
针对检测器数目和检测器对非我空间的覆盖之间的矛盾,文献[92]提出基于模拟退火算法的负选择算法,以此增加检测器对非我空间的覆盖区域。文献[93]提出基于欧氏距离的实数域负向选择算法,并应用于周期性时间序列和转子振动时间序列,结果表明,该算法可以有效地检测出异常值。文献[94]提出采用粒子群算法的优化检测器的分布来提高检测效率,作者将该算法应用于正弦时间序列和轴承振动信号序列验证了该算法的有效性和实用性。文献[95]提出改进的进步训练负选择算法(Further training NSA,FtNSA),通过生成覆盖自区域的自检测器引入到训练阶段以减小“漏洞”,作者将该算法应用于多个实验数据集,结果显示其在整体上要明显优于NSA,同时表示会将优化生成的检测器分布和减少检测器重叠作为今后的研究方向。文献[96]提出基于网格文件的特征空间负选择算法(Real NSA based on the Grid File of feature space,GF-RNSA),将特征空间划分为若干网格单元,然后在每个网格单元中分别生成检测器。由于候选检测器只需要与位于同一细胞内的自身抗原进行比较,而不需要与整个自身集进行比较,因此检测器训练结果更加有效。文献[97]提出基于粒子群优化的负选择算法(NSA based on Particle Swarm Optimization,NSA-PSO),即利用粒子群优化算法改进随机检测器的生成,将该改进算法应用于垃圾邮件检测网络,结果表明该算法的结果优于传统的NSA算法。
文献[98]认为上述算法虽然都能够在一定程度上减少“漏洞”,但是几乎没有考虑到检测器在小样本情况下的在线自适应能力,因此作者提出在小样本情况下的在线自适应学习的边界固定负选择算法(Boundary-fixed Negative Selection Algorithm with Online Adaptive Learning,OALFB-NSA),实验结果表明,该方法能够适应测试阶段自身空间的实时变化,具有较高的检测率和较低的误报率。
3.4 基于聚类的算法
聚类是一种非监督的算法,符合实际工程数据标签不完整、不准确的情况,因此在异常检测领域有比较广泛的应用,目前已有的聚类算法主要包括K-means、基于密度的聚类方法DBSCAN(Density-Based Spatial Clustering of Applications with Noise)、高斯混合模型(Gaussian Mixture Model,GMM)等。文献整理发现,时间序列的异常发现主要结合的算法是K-means[99],该算法是一种基于划分的聚类方法,该算法简单高效,适用于对大规模数据集的处理。
但是传统的K-means 算法的聚类结果易受初始聚类中心和离群值的影响。为解决该问题,文献[100]提出最近最远K均值算法(minimum maximumK-means,minmaxK-means),该算法能够保证各距离中心保持一定的间隔,但是不能消除离群点对算法的影响;文献[101]提出通过计算各个数据点的密集性,利用密集性最大的前K点作为初始聚类中心的思想,但单纯利用密集性选取的初始中心并不能保证均匀分布,不太符合聚类的真实位置和本质属性。之后,文献[102]提出了改进的K-means 算法,该算法结合前文改进算法的特点,首先剔除离群点区域,然后在数据紧密区,对算法的初始聚类中心按照最近最远距离的原理选择初始聚类中心。实验证明,改进后的K-means 算法在异常检测率、误报率等方面均优于传统的K-means 算法和minmaxK-means 算法。文献[103]提出一种基于高斯函数加权距离测度的改进的粗糙K均值算法(RoughK-means,RKM),与传统算法相比,该算法能够在同样的时间复杂度下,为数据集提供更为合理的上下界,其聚类效果更加精确。另外,文献[104]将K-means 算法结合计算多维时间子序列之间距离的扩展范式距离(the Distance of Extended frobenius norm,DEros),将聚类从发现异常点扩展到能够发现多维时间子序列,但是该算法的复杂度较高,同时不能进行在线异常检测。文献[105]将K-means 算法和基于距离的算法结合,提出两阶段的多维时间序列异常检测算法,首先利用K-means 进行初始聚类,并用一个启发式规则估计每个簇包含异常点的可能性,按从大到小的可能性进行排序;然后在聚类基础上,利用循环嵌套算法实现异常检测。该过程增加了两个剪枝规则,从而降低了时间复杂度,但是该方法对由不同密度子集混合而成的时间序列数据集的检测效果不好[106]。
3.5 基于分类的算法
分类算法是有监督的方法,例如支持向量机(SVM)、K近邻(K-Nearest Neighbor,KNN)算法、决策树算法。文献整理发现,目前分类算法中用于解决时间序列异常检测问题的主流算法是SVM算法和其改进算法1-SVM。
SVM 的优点是泛化能力强、没有局部极小点和解具有稀疏表示,因此被经常应用于入侵检测系统的异常检测中[107]。另外,SVM 在异常检测领域结合其他算法能够得到很好的检测效果,文献[76]将ARIMA结合SVM算法实现多维时间序列的在线异常检测,结果显示该算法的有效性。文献[108]提出改进的SVM 算法,结合神经网络解决植物病害检测问题。文献[109]提出局部增量算法LISVM(Local Incremental SVM),结合径向基函数改进SVM,能够实现在线分类,在实验验证中该算法具有良好的表现,同时其计算复杂度不高,可以从扩大实验数据规模和调整参数两个方面进一步优化该算法。
文献[110]认为异常值检测实际上可视为特殊的一类分类问题,即1-SVM,其将1-SVM 从回归和相空间重构分类两个角度对时间序列进行异常检测,分别提出根据求最小超球体的二次规划方法和基于线性规划的优化方法,实验结果表明以上两种方式均能较好地辨别出时间序列中的异常值。文献[111]PCA 结合1-SVM 的算法,首先利用PCA 进行维数约简,利用滑动窗口对降维后的数据集进行区域划分,然后对时间窗内的数据进行特征提取并转换为无序变量,最后将其代入1-SVM 进行训练,实现对待测数据的异常检测,该算法简单,在实际的工程应用中起到较好的效果。
3.6 研究趋势
异常发现主要分为两种思路:第一种思路是将预处理后的多维时间序列转换为多个单维时间序列分别进行分析,同时结合聚类算法、分类算法实现对多维时间序列的异常检测;第二种思路是直接将多维时间序列切割成若干个多维时间子序列后通过聚类算法等方式进行异常发现。
目前该领域的实现方式主要基于第一种思路,该思路的理论研究相对成熟,但是对应算法基本不能满足实时异常检测,同时其对数据预处理的方式比较敏感,另外随着数据集规模的增长,该算法时间复杂度会大幅增加,不能满足今后的数据发展需求。
第二种思路目前处在初步研究阶段,但是由于该方法能够在同一时刻保留各个维度之间的相互关系,并且不需要通过训练多个模型来实现异常检测,能够满足大规模数据类型的需求,因此对于该算法的研究对于大规模数据更具有价值。从文献整理来看,目前该领域存在的研究难点在于难以衡量多维时间子序列之间的相似程度。总结该思路算法的研究重点主要为以下几个方面:
1)多维时间子序列相似性度量算法研究。据了解,目前该领域相对常用的算法是基于扩展范式距离的度量方法,但是该方法不满足实时异常检测,仍需要学者进行算法改进或者提出新的算法。
2)基于单维时间序列异常发现的算法改进。目前对于单维时间序列进行分析的算法主要是基于预测的算法和基于概率的算法,这两种方法目前已经比较成熟,可以通过相应的算法改进来研究多维时间序列的问题。
3)改进传统的聚类和分类算法,使其满足时间特性。传统的聚类和分类算法的对象是无序变量,但是时间序列是有序数据集。为避免丢失时间序列的时间维度信息,在研究时间序列问题时,需要对传统的聚类和分类算法进行相应的算法改进。
4 结语
随着信息技术和硬件制造水平的提高,各类数据均能够通过前端设备实时采集,形成规模愈加庞大的海量时间序列,为多维时间序列异常检测的发展提供了契机和挑战。
近年来,国内外在该领域的理论研究已有一定的成果。通过文献整理,本文归纳为两种主流思路:第一种是将原始多维时间序列经过数据预处理之后转换为单维的时间序列,然后利用单维时间序列异常检测的相关理论发现异常;第二种是通过研究新的算法或者改进算法直接对预处理后的多维时间子序列进行异常检测。
目前对于第一种思路的理论研究相对成熟,但是该思路比较适合对于小型数据的异常检测。第二种思路目前虽处在初步研究阶段,但是该思路理论上能够满足更大规模时间序列的异常检测,因此本文认为今后的发展研究方向将侧重于第二种思路的理论研究。
下面从“维数约简”“时间序列模式表示”和“异常模式发现”三个方面对第二种思路的重点研究内容进行总结。
1)维数约简:算法在时间相关性方面的优化研究。维数约简过程中如何保留原始数据的时间规律是目前已有算法难以解决的问题,虽然学者已有初步成果,但是目前在该领域仍然没有普遍认可的方法。
2)时间序列模式表示:多维时间序列模式表示的方法研究。该方法的难点主要在两个方面:第一,难以确定统一的规则,使其能够在较高数据压缩率的情况下,对各个维度具有比较精确的表示;第二,该方法是否能够适用于实时更新的多维时间序列。
3)异常模式发现:该领域主要研究方向可以分为两个部分:第一,多维时间子序列相似性度量算法研究;第二,聚类和分类算法在时间相关性方面的优化研究。目前已有许多经典的单维时间序列相似性度量方法,例如欧氏距离、动态时间扭曲、垂直距离等,但是对于多维时间序列的相似性度量方法还处在初步研究阶段,目前还没有成熟的算法理论。另外,传统的聚类、分类算法只是针对无序变量,如直接应用于时间序列会丢失原始数据信息,降低异常检测的准确性,因此有必要聚类和分类算法进行改进和优化。
除此之外,在对多维时间序列异常检测的算法研究中,要注意以下问题:第一,要尽量降低算法的复杂度。过度复杂的算法不仅要消耗较多的时间和存储代价,同时也不利于参数的调整,难以达到预期的效果。第二,算法要注重对实时检测的研究,在实际的应用中,多维时间序列大部分均需要进行实时异常检测,因此要求算法能够在较短的时间内有效判断出最新数据的状态,这对算法的实时性提出了更高的要求。第三,注重算法的鲁棒性和泛化能力,保证算法能够在不同的实际工程背景下尽量得到稳定和精确的结果。
总的来说,多维时间序列异常检测领域的理论研究并不成熟,建议今后的理论研究要更多地结合实际应用背景,以实际、动态、大规模的工程数据集为检验算法可行性的主要依据,从而进一步地提高和完善理论研究成果。

