关于伽马射线暴喷流结构模型的研究

栾天成, 郝景萌

(广州大学 物理与材料科学学院， 广东 广州 510006)

0 引 言

伽马射线暴(简称伽马暴)是宇宙中最剧烈的能量释放现象，是一种来自宇宙中的伽马射线在短时间内迅速增强随后又减弱的现象.关于伽马暴的起源以及其形成的物理机制，从20世纪60年代被发现至今，一直都是天体物理学中的热门话题.根据其持续的时间长短，伽马暴可以被分为两种类型：长暴(持续时间大于2 s)和短暴(持续时间小于2 s).近年来，有越来越多的观测证据表明[1-3]，长暴是来源于大质量恒星塌缩的产物[4-5]，而短暴是源自于致密双星系统(双中子星或一个中子星一个黑洞)的合并[6].为了能够更好地理解伽马暴的前身星系统以及它的中心引擎，对于产生伽马暴的喷流张角和能量结构的限制是至关重要的[7-8].在之前的研究中，人们更倾向于假设伽马暴喷流能量是存在着特殊的角结构的，而并非是最简单的各向同性辐射[9-12].特别地，Zhang等[13]考虑了一个具有高斯分布的能量角结构模型并尝试去解释伽马暴的观测性质.Pescalli等[14]探讨了具有幂律分布结构的伽马暴喷流对其光度函数的影响.Salafia等[15]还在其工作中进一步探索了这两种不同角结构模型的性质.基于观测值EX/Eγ(各向同性等值的早期X射线余辉能量与伽马能段能量的比值)，以及长暴的光度函数，Beniamini等[16]探讨了伽马暴的各种喷流角结构模型.另外，引力波与伽马暴的联合探测也被用来限制不同的喷流角结构模型[17].总的说来，以上提到的高斯、幂律分布的喷流能量结构模型，加上标准均匀分布模型目前正在被广泛地研究与讨论，尽管到目前为止,人们对于最适合的喷流结构模型及其对于伽马暴各种观测特征的潜在影响，仍然没有达成共识.

本文研究了伽马暴喷流的各种能量角结构模型对其能量及红移分布的影响，再利用伽马暴的可用观测数据并结合蒙特卡洛模拟的方法，来尝试限制喷流角结构模型.因为相较于短暴，长暴有着更大并且更完备的样本，本文的讨论仅限定于长暴.本文第一节中，介绍不同的喷流结构模型和所采用的蒙特卡洛模拟方法；在第二节中，给出模拟的结果；在第三节中，进行总结与讨论.本文中所采用的宇宙学参数是H0=71 km s-1Mpc-1,ΩM=0.3,ΩΛ=0.7.

1 喷流模型和蒙特卡洛模拟

1.1 喷流模型

在本工作中，将考虑三种之前被广泛研究和讨论的喷流角结构模型.第一种是标准均匀分布喷流模型[9]：该模型假设单位立体角内的能量ε(θ)在喷流锥形张角内部是一个常数，而在张角的外部则为0.其公式如下：

(1)

其中，θj是喷流的半偏角大小.之前的研究一般将该角度的大小限制在5°～15°之间[18-20].本文中，为简单起见，只选取3个固定的角度值进行研究，即θj=5°、15°和30°.另两种模型就是所谓的有结构的喷流模型，这类模型中的喷流都具有固有的各向异性特征，而伽马暴的变化则主要取决于不同的观测角度θv.对于幂律分布和高斯分布喷流模型，ε(θ)作为随喷流轴夹角变化的函数，分别为[21]

(2)

和

ε(θ)=ε0e-(θ/θ0)2

(3)

其中,θ0代表着喷流锥的典型半偏角大小，在本文中θ0取值设为2°.特别地，对于幂率分布喷流模型，考虑a=2和4这两个不同的值.因此，伽马暴喷流的总能量Ej可以通过在所有立体角内对ε(θ)积分得到：

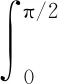
(4)

伽马暴的各向同性总能量Eiso则可以简单地通过下式的计算得到：

Eiso=4πε(θv)

(5)

1.2 蒙特卡洛模拟

为了更好地说明伽马暴的喷流结构模型是如何影响其能量与红移分布的，利用蒙特卡洛模拟方法生成了一个长暴的模拟样本.每一个通过模拟产生的长暴都以一组参数标识，即红移z、总能量Ej和观测角度θv.这三个参数分别根据以下假设通过随机过程生成：

(1)伽马暴的红移由一个概率分布函数p(z)给出.该函数可以通过对长暴的固有爆发率在红移z=0～10区间进行归一化得到，其形式为

(6)

其中,Az是归一化常数，dV/dz是在单位红移内的共动体积元，而Θ(Zth,z)则表示金属丰度在阈值Zth以下的恒星质量占比[22]，其形式为

(7)

(8)

(2)总能量可以从一个对数正态分布的概率分布函数得到，其形式为

(9)

其中，AE是归一化常数.上式中正态分布的中心值Ec和标准差σEj是自由参数，它们的值可以通过与观测之间的比较来限制.

(3)分配给每一个事件一个观测角度，该角度可以通过概率分布函数p(θv)dθv=sin(θv)dθv在范围[0～π/2]内得到.对于均匀分布模型的情况，如果观测角度θv>θj，那么这个伽马暴将无法被探测到.但是对于有结构的喷流模型而言，喷流并不存在一个明确的边界.

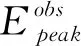
logEpeak=-29.6+0.61logEiso

(10)

(11)

其中,dL是光度距离，k(z)是k改正因子，可以通过下式计算：

(12)

其中,N(E)代表观测者参考系中的光子数能谱.

1.3 一致性检测

1.3.1 观测样本的选取

截至2018年7月底，Swift-BAT共计探测到了1 247个伽马暴(从GRB041217到GRB180728)[32]，从中选取628个通量大于阈值F[15-150]≥10-6erg cm-2的长暴.在这些源中，有271个长暴是有红移探测的，本文将这271个长暴作为对比与分析的观测样本.

1.3.2 模型与观测的一致性检验

模型有两个自由参数，即Ec和σEj，用以表征喷流总能量的对数正态分布.对于每一对所选取的自由参数，运行一遍模拟程序以生成由104个“被探测到”的伽马暴所组成的一组模拟样本.然后，与Kanaan等[33]的方法类似，先计算模拟伽马暴样本的通量分布，并通过与Swift-BAT观测到的真实样本进行比较来限制不同喷流模型下的这两个自由参数.模拟样本与观测样本的通量分布一致性可以通过2检验来判定：

(13)

其中,fi,obs和fi,sim分别代表在第i个区间块中的观测与模拟样本通量的概率.在不同的自由参数组合下，通过不断重复上述蒙特卡洛模拟步骤，最终找到2值最小的一对自由参数，而这对参数值便代表了最优的参数选择.

2 结 果

表1给出了与观测样本的通量分布符合最好的自由参数组.对于不同的喷流结构模型，能量中心值Ec的差别并不是很大，基本所有模型都处在50附近，除了a=2的幂律分布模型要偏大约2个数量级.这些结果表明,除了a=2的幂律分布模型，伽马暴的喷流总能量可能要比直接通过观测推导出的各向同性能量少2个数量级以上.

表1 卡方最优参数列表

Table 1 Best parameters constrained by 2

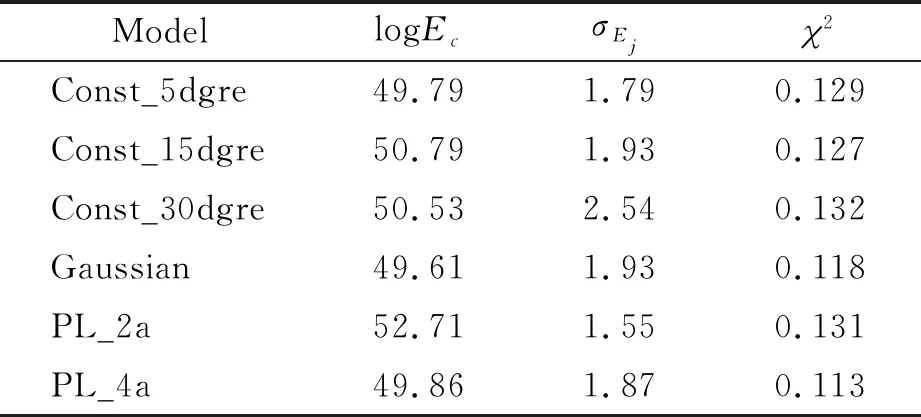
表1 卡方最优参数列表

ModellogEcσEj 2Const_5dgre49.791.790.129Const_15dgre50.791.930.127Const_30dgre50.532.540.132Gaussian49.611.930.118PL_2a52.711.550.131PL_4a49.861.870.113

在确定最优自由参数组之后，可以进一步得到各种喷流模型下模拟伽马暴样本的红移和各向同性的总能量分布，并与观测进行比较.图1给出了均匀分布模型下伽马暴各向同性能量Eiso的分布与观测的比较.其中喷流张角分别取值5°、15°和30°，并以实线、虚线和点虚线表示.然后利用Kolmogorov-Smirnov(K-S)测试来检验模拟与观测样本之间的一致性.结果发现，在3个角度中，只有当θj的取值为30°的时候，K-S 检验的结果给出P>0.05，这意味着Eiso的分布与观测比较一致，而对于5°和15°的情况，K-S 检验只给出P<0.05.高斯分布模型和幂律分布模型与观测的比较分别见图2～图3.对所有模型K-S检验的结果都小于0.05.

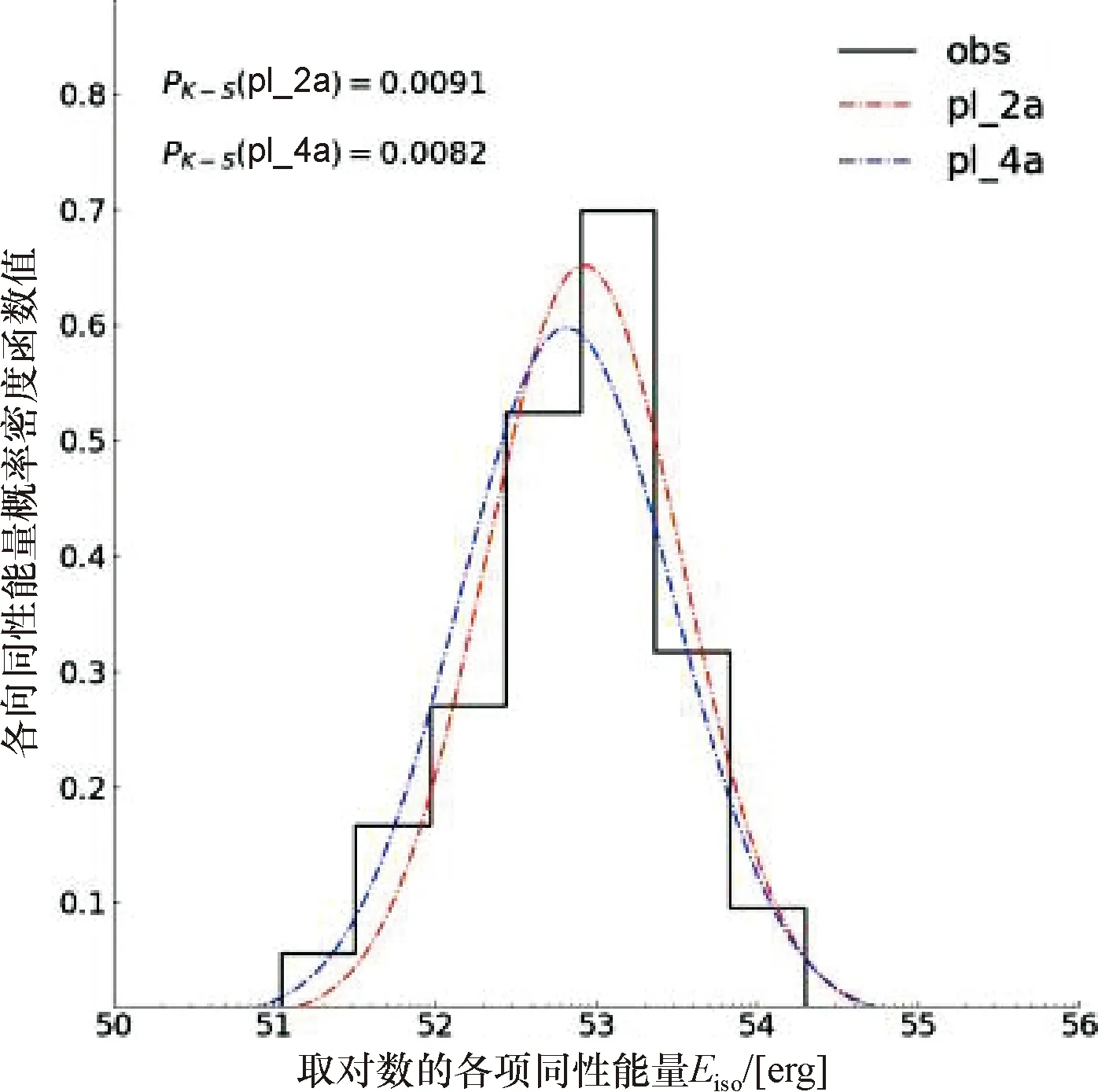
图3 幂律喷流分布模型模拟的各向同性能量概率密度分布图

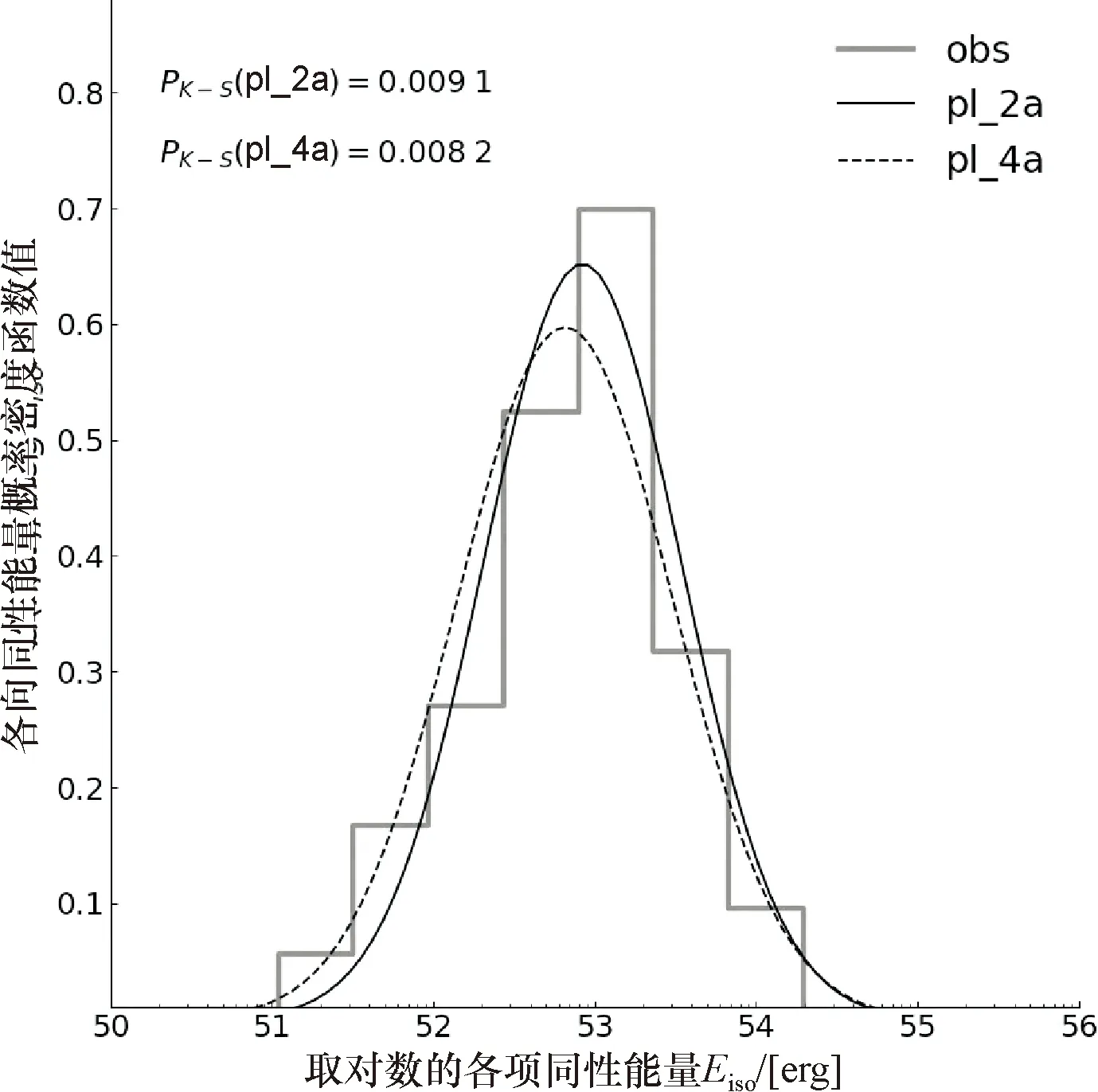
图2 高斯喷流分布模型模拟的各向同性能量概率密度分布图

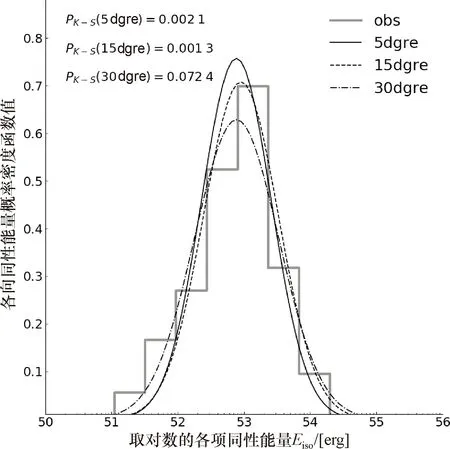
图1 均匀喷流分布模型模拟的各向同性能量概率密度分布图

对于红移而言，三种喷流张角结构模型(常数、高斯和幂率)的红移与观测红移的累积分布分别见图4～图6，其中对应的与观测红移分布之间的K-S检验P值已在各自图中右下角标出.无论是对于均匀分布模型，还是对于高斯分布和幂率分布模型，给出的结果区别都不大，K-S检验都得出了一个相当低的概率(P<0.05).所有模型都低估了低红移伽马暴的数量.

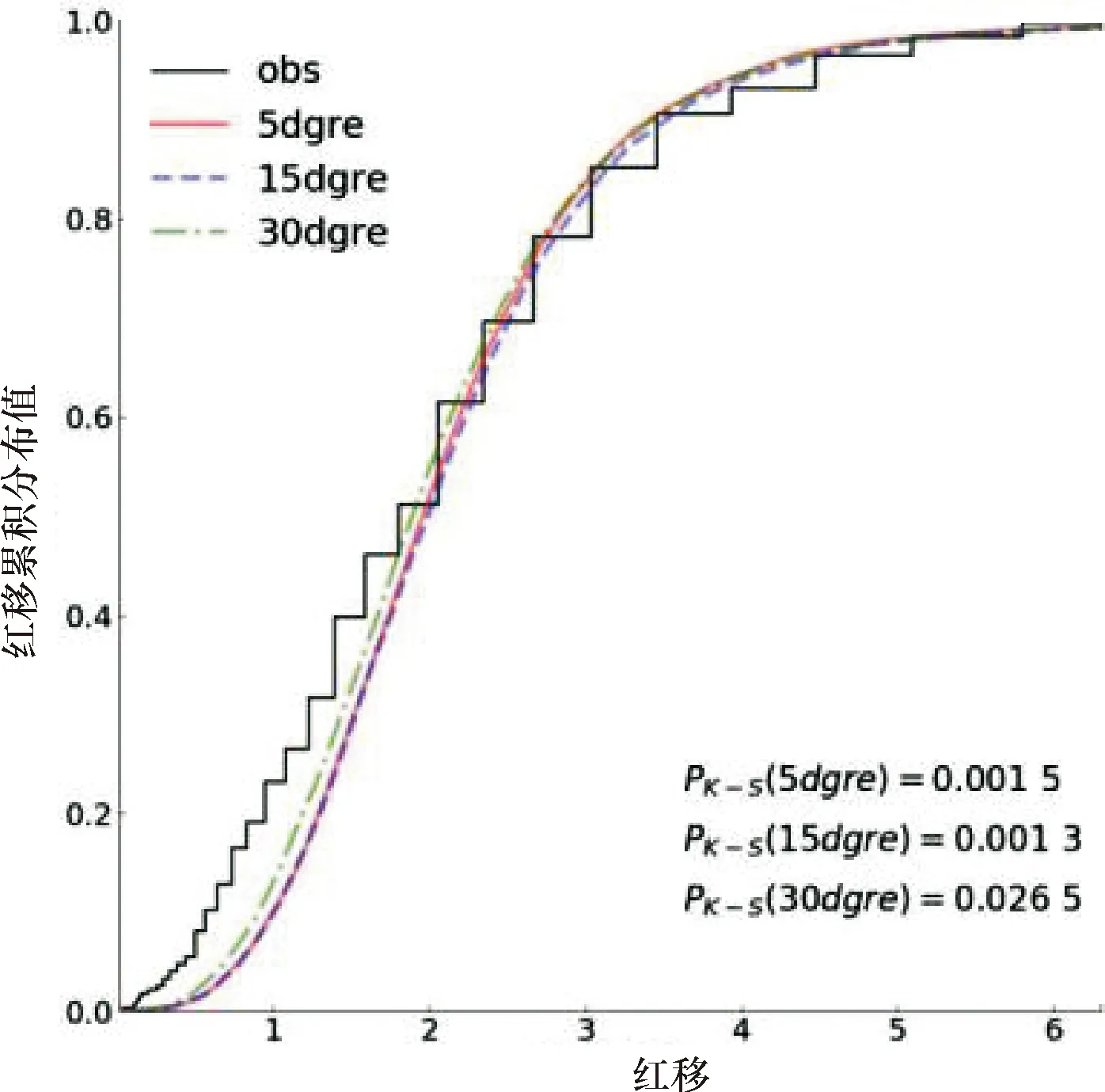
图4 均匀喷流分布模型模拟的红移累积分布图

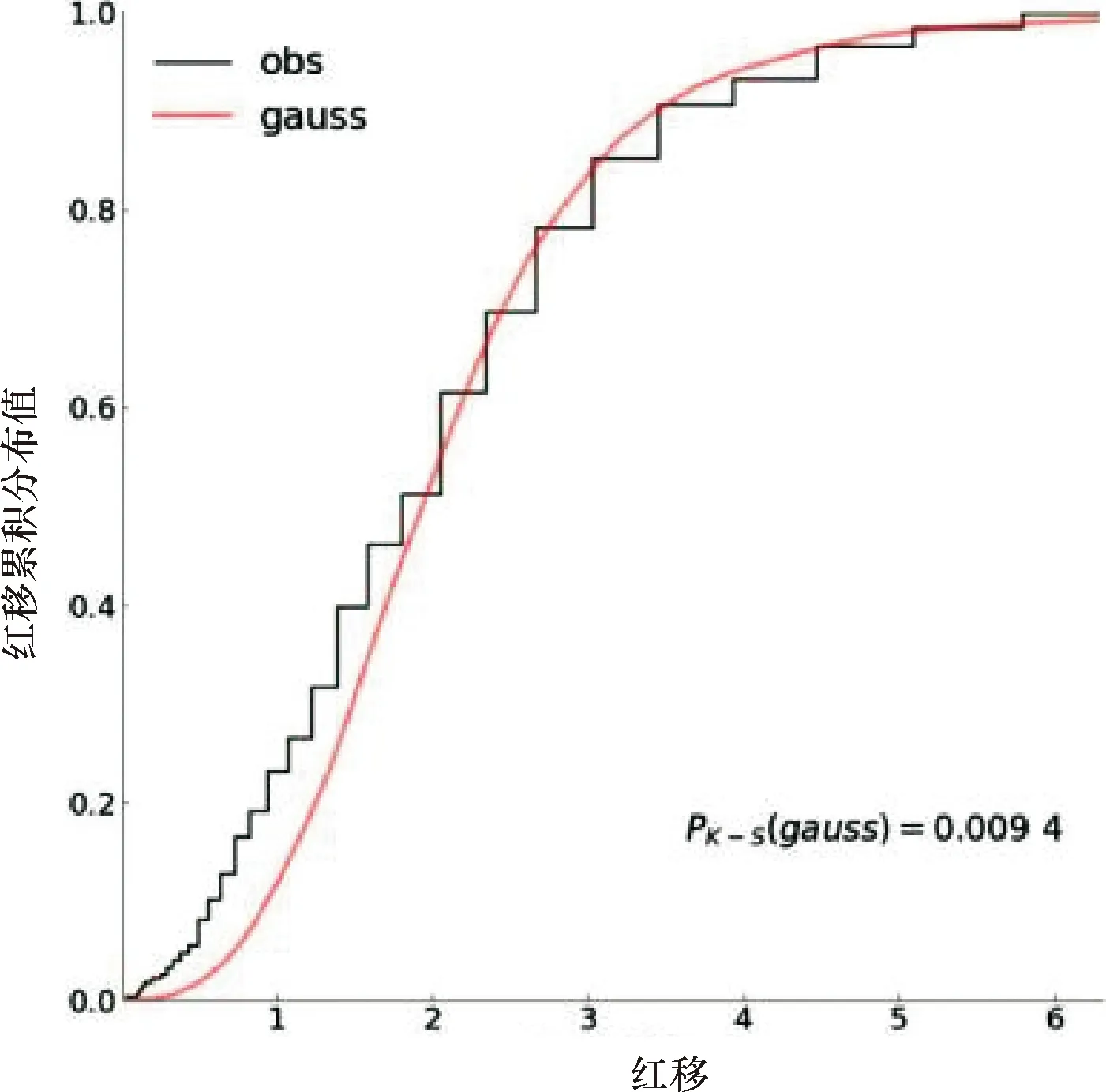
图5 高斯喷流分布模型模拟的红移累积分布图

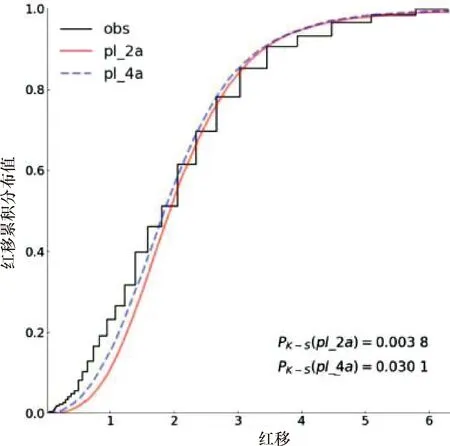
图6 幂律喷流分布模型模拟的红移累积分布图

3 总结与讨论

了解伽马暴的喷流张角和能量结构对于进一步理解伽马暴的前身星系统以及它的中心引擎是至关重要的.本文利用蒙特卡洛模拟的方法，研究了均匀分布、高斯分布及幂律分布三种伽马暴喷流的能量角结构模型对其各向同性能量及红移分布的影响.首先，通过模拟样本与观测数据的通量分布的比较，限制了不同模型下假设为对数正态分布的伽马暴喷流总能量分布的特征参数.发现能量中心值分布在49.790.05).然而对于红移分布，所有模型的结果都比较相似，并且与观测符合得不是很好.模拟与观测的区别主要来自于低红移端，说明所有模型都低估了低红移伽马暴的数量.总之，目前的观测数据可能还不足以区分三种喷流模型.

模拟结果与观测的差异可能来自于以下两个方面：①模拟所采用的模型比较简单.一方面，模型中很多参数都被设为了定值，例如，金属丰度阈值等；另一方面，为了简化计算，忽略了喷流的相对论效应、伽马暴光度函数和喷流张角等可能存在的红移演化；②简化了Swift-BAT探测器的探测标准.在本文中，采用了一个单一的通量阈值作为伽马暴能否被探测到的标准.而事实上，Swift-BAT的伽马暴触发机制非常复杂.因此，低通量伽马暴的截断有可能会导致低红移伽马暴的低估.

在后续工作中，笔者会持续改进工作，例如，考虑一个更复杂的模型，采用更好的阈值标准，使用马尔科夫链氏蒙特卡洛(MCMC)方法替代蒙特卡洛方法直接从离散观测样本分布中采样，还有增加观测数据上的限制，进一步探究各种因素对喷流模型的影响，从而能对模型进行更好的限制.