以任意高维纠缠态为量子信道的受控隐形传态

彭家寅

内江师范学院 数学与信息科学学院，四川 内江641199

1 引言

1993年，通过量子力学资源传输量子态的思想是由Bennett等人[1]于1993年率先提出，他们使用Einstein-Podolsky-Rosen对和经典通信，将一个单粒子未知量子态从发送端传送到远程接收端，而没有传输量子态载体本身。在光学实验中，用偏振光子[1]和单相干场模式[2]实现了量子态远距离传输。在Bennett等[1]的开创性工作之后，一些研究者利用不同类型的量子信道，设计出了许多隐形传态协议[3-13]。其中大多数的隐形传态方案涉及到了一些特定的量子信道，如二维希尔伯特空间中EPR对的复合态或多粒子纠缠态。

受控隐形传态[14-20]是隐形传态的一种扩展版，其接收者只有在监控者的许可下，才能重构发送者的原始量子态。1998年，Karlssion和Bourennane[14]率先提出以三粒子GHZ态为信道来传递一个单粒子态的受控隐形传态协议。2004年，Yang等[17]提出了传输多量子信息的多方受控隐形传态协议。2005年，Deng等[18]提出了任意二粒子纠缠态的受控隐形传态方案，该方案可以不加任何修改地直接用于受控隐形传态。Zhou[19]和Dong[20]等提出利用非最大纠缠态作为量子信道、任意多个粒子的态的多方受控隐形传态方案。文[21-23]研究了多方分享多维量子态协议，这些协议也可以直接作为多方受控隐形传态方案。相对而言，高维量子比特比二维量子比特携带更多的信息[24]。通过将几个量子比特组合成一个单一的、高维的系统，这些量子比特之间的门变成远小于二维量子比特的单个高维量子比特的操纵，这可能更可靠。但值得注意的是，在上述所有方案中，发送者要传送的态的粒子维数与量子信道中粒子的维数是相同的。最近，Zhan等[25]用三维纠缠态作为信道，提出一个关于二维单粒子态的隐形传态的协议，并将之推广到用任意d-维纠缠态作为信道、关于传递f维的量子隐形传态的情况(d＞f)。接着，给出了采用不同维数的量子信道，远程地执行单量子未知酉算子的一个协议[26]。

本文在文献[25]的基础上，研究高维信道的受控隐形传态问题。首先以三维量子纠缠态为信道，建立起发送者、接收者和控制者三方合作传送二维未知单量子态的方案，并将之推广到d-维量子纠缠信道的t-维未知单量子态传输情形(d＞t)。

2 以三维量子态为信道态的受控隐形二维单量子传态

为了讨论方便，首先考虑(3×2)-维Hilbert空间中的如下一个最大量子纠缠态：

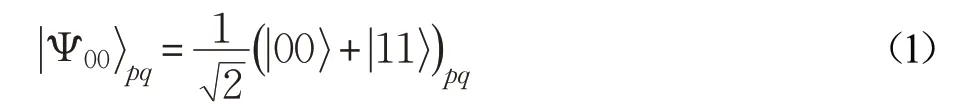
其中，p是三维Hilbert空间中的粒子，而q是二维Hilbert空间中的粒子。容易计算得到：作用在粒子p上的单体算子：

这里m′=0,1,2；n′=0,1。

现在考虑量子隐形传态方案：假设在监控者Charlie的控制下，Alice想要把任意未知二维单量子态：

传送给Bob，这里，α和β是任意复系数且满足 ||α2+|β|2=1。Alice、Bob和Charlie事先安全地分享如下一个三维量子纠缠态：

其中，粒子A、B和C分别属于Alice、Bob和Charlie。整个系统的态可以表示成：

3 以d-维量子态为信道态的受控隐形t-维单量子传态

将第2章结果推广到更一般的情形。为此，考虑一个(d×t)-维Hilbert空间中的最大纠缠态：

其中，p是d-维Hilbert空间中的粒子，q是t-维Hilbert空间中的粒子，且p＞q。单体变换：

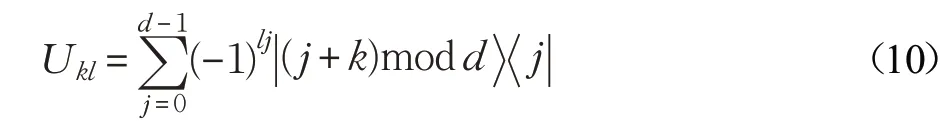
其中，k=0,1,…,d-1；l=0,1,…,t-1。具体地：

将单体变换Ukl作用在粒子p上，可将

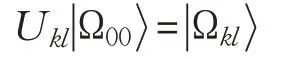
具体如下：

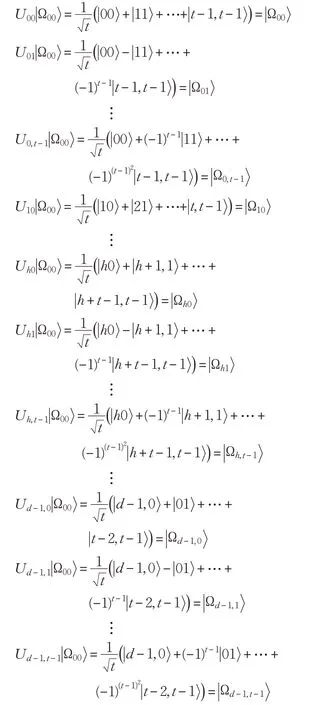
其中，k=0,1,…,d-1，l=0,1,…,t-1。

下面转到本文的方案上来，假设发送者Alice、接收者Bob和监控者Charlie事先分享如下所示的d-维量子态：

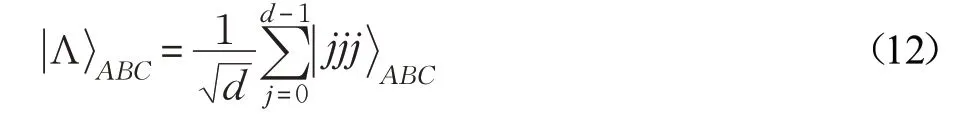
其中，粒子A B和C分别属于Alice、Bob和Charlie。假定Alice希望将如下一个t-维单粒子未知态传送给Bob：

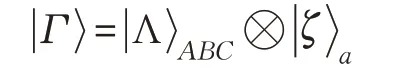
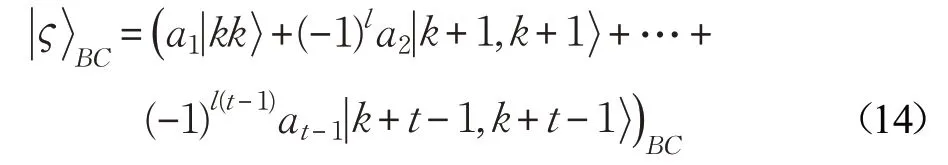
Charlie收到信息后，若他愿意合作完成任务，那么他用如下所示的基：

其中，r=0,1,…,d-1，对粒子C进行测量，并将测量结果通知Bob。如果测量为，则粒子B的态变为：

Bob根据Alice和Charlie的测量结果，并对粒子B执行如下所示的d-维酉变换

(s,t=0,1,…,d-1)中的适当变换Wr0，则变成：

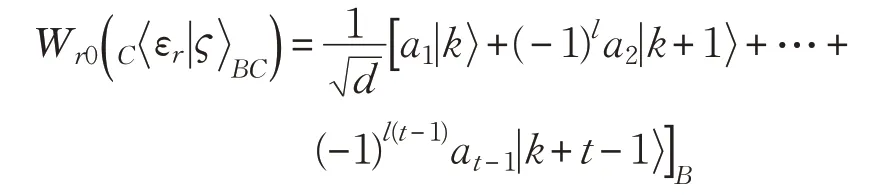
然后，对粒子B施行式（10）所示的单体变换Ud-k,0，有：

再对粒子B施行单体变换U0l，于是

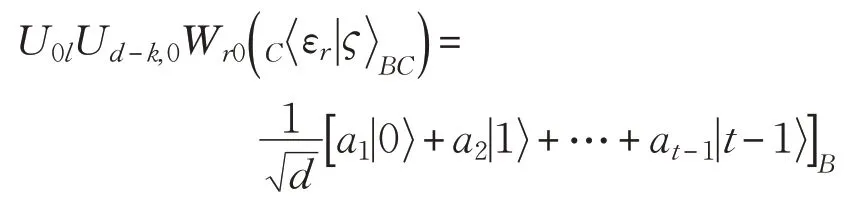
这表明Bob已经获得了Alice的原始秘密，从量子任务完成。

4 结论

在几乎所有的现有量子隐形传态协议中，发送者要传送粒子的系统Hilbert空间的维数等于发送者与接收者分享的量子信道的维数。然而，真实世界中量子通信的各方事先分享的量子态的维数不总是与所要传输的量子态的维数相同，特别是在某种紧急情景下，需传递特殊的量子信息时，这种维数的不一致是完全有可能出现的。从而，研究高维量子信道的隐形传态是有必要的。

为此，本文首先给出利用三维量子信道去传送二维单量子未知态的方案，该方案要求发送者Alice对她的粒子对进行非对称基测量，监控者Charlie对自己粒子广义单粒子投影测量，而接收者Bob需对其粒子执行三维酉变换和单体变换。此后，将上述方案进行了推广：把三维量子信道换成d-维量子信道，将二维单粒子未知态传输换成小于d的任意f-维单粒子未知态的传输，方案仍然能够以100%的概率成功实现。当然，上述两个方案的实现都离不开监察者的许可；否则，隐形传态任务失败。此外，利用单体变换构造了两组非对称正交测量基，它们是这些方案中的一个关键要素。局部高维酉变换、单体变换和经典通信也是本文方案要求的。由于受控隐形传态在网络量子信息处理和加密协议中非常有用[27]，因此本文的方案有助于拓展量子信息科学的隐形态领域。