基于 5 MW 风机模型的变初值模糊 PI 变桨控制技术研究

司荣国，贾成真，王灵梅，鲍玉涛，刘玉山，陈立明

（1.青海省绿色发电集团股份有限公司， 青海 西宁 810001； 2.山西大学 山西省风电机组监测与诊断工程技术研究中心， 山西 太原 030013； 3.阿尔斯特大学 计算机学院， 北爱尔兰 贝尔法斯特 BT370QB）

0 引言

随着能源危机的加剧， 风力发电在许多国家和地区呈现井喷式发展[1]， 从2007 年到2017年，风力发电的年增长率达到了49.18%[2]。由于风电机组正在向大型化发展，风电机组的非线性动态特性更加明显[3]。 作为风电机组的核心技术之一，当风电机组在额定风速以上运行时，先进的变桨控制算法对机组安全、稳定运行至关重要。

在额定风速以上，风电机组为了避免机组超速，通常采用调整桨距角的方式，改变气流对叶片的攻角使机组功率保持稳定[4]。 目前国内外风电机组大多采用PID 控制算法完成变桨距控制，但由于风速的随机性和机组的非线性， 线性的PID 控制算法不能取得满意的控制效果[5]。文献[6]针对300 kW 变桨距风电机组设计了基于风速的非线性前馈控制器，提出了前馈与模糊PID 相结合的变桨控制算法。文献[7]采用RBF 神经网络非线性算法，通过在线调整神经网络权值来改善风机变桨系统在运行区域内的动态性能。 文献[8]引入了平滑函数模型，避免了直接切换导致桨距角输出的不连续而带来的系统振荡问题。 文献[9]提出统一变桨距的双模糊控制算法， 与传统控制算法相比，降低了控制器参数调整的频率。 文献[10]为增强变桨系统的抗干扰能力， 提出了模糊自抗扰的变桨控制方案，实现了控制器参数的自整定。文献[11]利用T-S 模糊推理，完成了模糊控制、模糊自适应PID 控制和PI 控制的软切换，使风机的桨距角调节更平滑， 输出功率精度更高。 综上所述， 目前的变桨距控制算法主要是解决传统PID控制算法针对非线性变桨控制问题的缺陷。

本文以FAST 软件中5 MW 陆上风电机组的非线性模型为研究对象， 提出了变初值模糊变桨控制算法。 通过拟合曲线的方法设计了初值调整算法，选取了合适的模糊规则和量化、比例因子，在Matlab/Simulink 中建立了具体的控制算法模型。仿真结果表明，提出的控制算法能够有效地保证风电机组在额定风速以上运行时转速的稳定控制，在降低机组受力、力矩波动方面效果明显。

1 额定风速以上风电机组变桨数学模型

风电机组通过叶片吸收风能， 把风能转化成机械能，经过传动链驱动发电机进行发电。在搭建风电机组模型时， 常假设风轮前方风的空间分布是均匀的，用动量定理可求得风轮吸收的风能。

式中： Pm为风轮吸收的风能； ρ 为空气密度； R为风轮半径；ν 为风速；λ 为叶尖速比；β 为桨距角；w 为叶轮转速；Cp（λ，β）为风能利用系数。

本文在分析变桨过程动态特性时，从包含转速一个自由度的系统运动方程入手，在简化的过程中，采用一阶泰勒展开式在稳定点（P0，w0）进行了近似处理，具体为

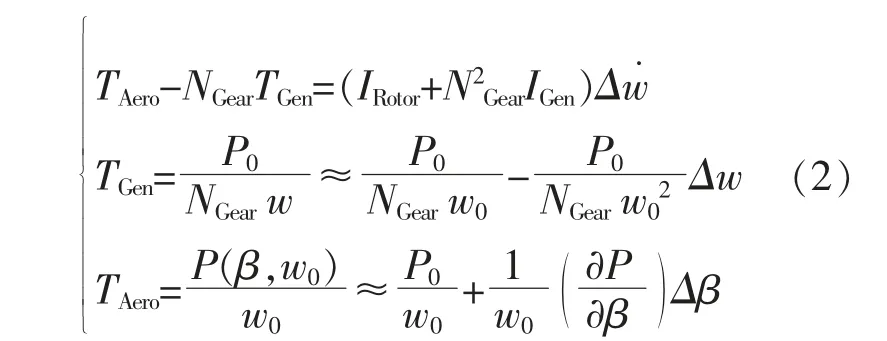
式中： TAero为叶轮的气动转矩； TGen为发电机转矩；NGeo为齿轮箱变速比；IRotor为叶轮转子惯性；IGen为发电机惯性；w0为叶轮的额定转速；Δw 为叶轮转速的微小扰动；Δw˙为叶轮的旋转加速度；P0为叶轮的额定机械功率。

当时间的变化量趋向无穷小时，w˙=Δw，则式（2）可以简化为

从式（3）可以看出，在额定风速以上运行时，风电机组变桨系统动态特性的非线性， 整个系统的输入是转速，输出是桨距角的变化量Δβ。

2 变初值模糊PI 变桨控制算法

2.1 变初值模糊PI 变桨控制算法结构

PID 控制算法的精髓是 “以误差反馈来消除误差”，直接取目标值与实际值之间的误差来消除误差的方式常常会造成系统响应“快速性”和“超调”之间的矛盾[12]，并且采用常规的PID 控制器对控制动态非线性对象往往达不到预期的效果。 传统的PI 变桨控制算法的原理为

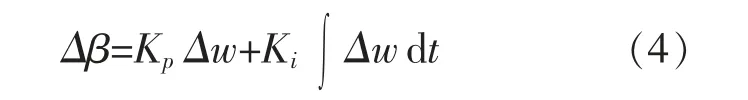
式中：Kp为PI 控制算法的比例系数；Ki为积分系数。

本文针对风电机组PI 变桨控制的缺陷，提出了变初值模糊PI 变桨智能控制算法，能够根据风速大小以及转速误差的大小、 转速误差的微分自动调节PI 控制器的控制参数，实现不同风况下的自适应优化控制。 算法的基本结构如图1 所示。

图1 变初值模糊PI 变桨控制算法结构图Fig.1 Structure diagram of Fuzzy-PI pitch control algorithm

由图1 可知：风力发电机的转速信号经过滤波算法与给定的额定转速作差，PI 控制算法把转速误差作为输入得出桨距角的变化量信号， 传输给风电机组的变桨执行机构； 模糊控制器通过实时计算转差和转差的微分，利用模糊规则，经过模糊化、去模糊得到PI 控制参数的变化量，另一方面，利用经过滤波的风速信号，通过变初值调整算法得到PI 控制算法不同工况下的PI 参数初值给定。整个控制算法能够实现不同工况下PI 控制算法参数的自动调节。

为了消除控制系统中风速和转速的高频激励， 通常采用一阶低通滤波算法对发电机转速和风速进行平滑处理，然后再引入变桨控制中。一阶低通滤波算法的原理为

式中：y（n）为滤波后第n 时刻的数值；x（n）为原始信号第n 时刻的数值；y（n-1） 为滤波后第n-1时刻的数值；α 为滤波系数，本文取0.99。

2.2 变初值模糊PI 变桨控制算法实现

变初值模糊PI 变桨控制算法主要通过制定合适的模糊规则和初值调整算法，实现对PI 参数的动态调节，具体原理为

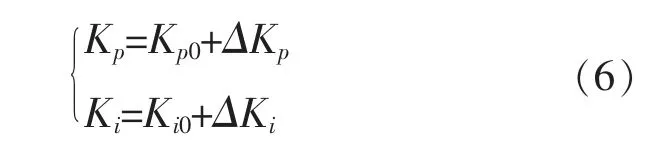
式中：Kp0，Ki0均为模糊PI 控制算法的初值， 根据风速的大小自动调整。

通过对转速误差和误差的微分进行模糊化，由模糊规则得出参数的变化量。

由于不同风速的变化会影响风电机组转速-桨距控制环的动态特性， 而控制器的控制参数直接影响控制效果的好坏。 通过对不同风况下控制器参数的调试，按照桨距角超调量小、响应快速的原则，PI 初值与风速的对应关系如表1 所示。

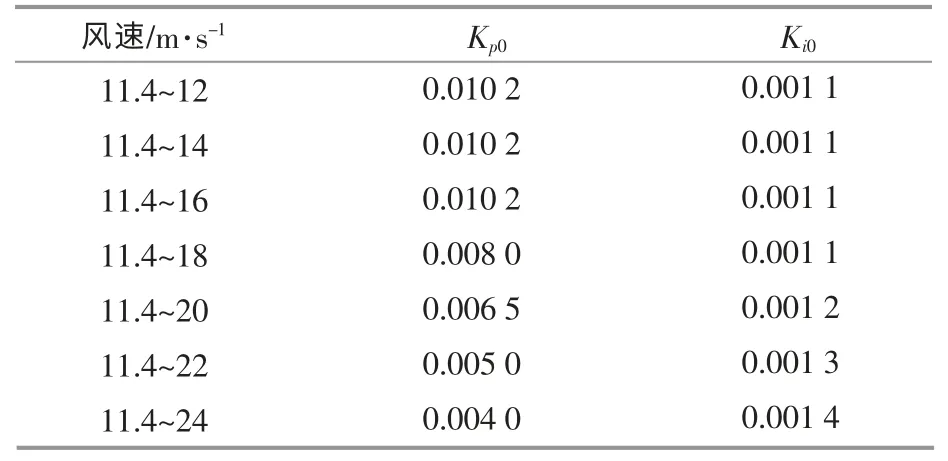
表1 PI 初值与风速的对应关系Table 1 The Corresponding relation between PI Initial value and wind speed

图2 为不同风速下变桨控制器对应的PI 参数初值的曲线图。 通过拟合曲线的方法得到了基于风速的初值整定算法。

图2 不同风速下PI 控制器的参数初值Fig.2 Initial parameters of PI controller at different wind speeds

风速达到24 m/s 时，已接近风电机组的切出风速， 所以在拟合时风速选择为11.4～24 m/s。经过分段拟合后，Kp0，Ki0的整定算法为

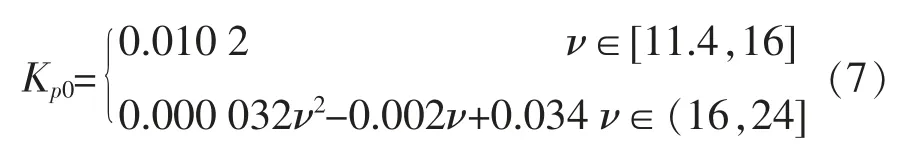
取模糊控制器的输入转速误差和误差变化率的基本论域为[-1，1]，因为转速误差的变化范围约为±100 rad/s，所以量化因子取0.01，输入输出的隶属度函数均采用变化平滑的正态分布函数，输入的模糊子集为{NB，NS，ZE，PS，PB}，NB，NS，ZE，PS，PB 分别表示负大、负小、零、正小、正大，输出量ΔKp的基本论域为[-1，1]， 比例因子为0.001，ΔKi的基本论域为 [-1，1]， 比例因子为0.000 1，输出的模糊子集为{NB，NS，ZE，PS，PB}。模糊规则见表2。

表2 模糊规则表Table 2 Fuzzy rule table

模糊规则的制定原则：当转速误差较大，误差的微分也较大时，尽量选择较大的ΔKp值，进而加快系统响应速度，适当选择负的较大的ΔKi值，防止系统出现超调； 当转速误差和误差的微分都较小时，ΔKp和ΔKi都选取较小的值。 采用重心法进行去模糊化，得到模糊控制器的输出。

3 仿真及结果分析

本文采用FAST 软件中5 MW 陆上风机非线性模型，FAST 风机模型计算的准确性获得了德国劳埃德船级社认证[13]，仿真的可信度较高，并且提供了接口文件，方便Simulink 调用。 为了便于比较，在Matlab/Simulink 中搭建了变增益变桨控制算法模型[14]和本文提出的基于风速的变初值模糊PI 变桨控制算法模型，风电机组模型的主要参数见表3。

表3 风电机组模型的主要参数Table 3 The parameters of wind turbine

续表3

增益PI 控制算法的Kp=0.018 8，Ki=0.008 06，模糊PI 控制算法的参数量化因子为0.01，比例因子分别为0.004，0.000 3，初值分别为0.008，0.001 1。

3.1 阶跃风速下控制性能仿真分析

为了验证控制策略的鲁棒性， 分别从额定风速11.4 m/s 变化到12，14，16，18，20，22 m/s 做阶跃风速仿真实验，比较了传统PI 控制策略、模糊PI 控制策略和变初值模糊PI 控制策略的控制效果（图3）。

图3 不同阶跃风速下的控制效果Fig.3 Control effect under different step wind speeds

由图3 可知，变初值模糊PI 变桨控制比传统的PI 控制提前了1～2 s。

通过对仿真数据的统计分析，得出3 种控制策略下桨距角和转速的对比效果（表4）。

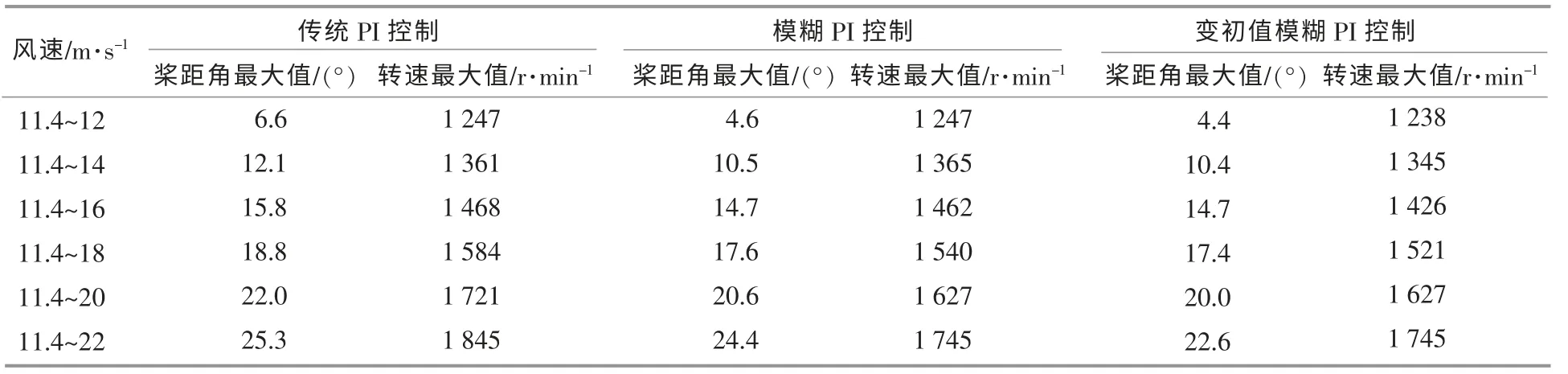
表4 控制效果对比Table 4 Contrast of control effect

由表4 可知，本文提出的控制算法比传统PI控制算法和模糊PI 控制效果好，尤其在低阶跃风速工况下，变初值模糊PI 控制算法能够保证桨距角和发电机转速更快地进入稳定状态。 由于风速信号的变化要超前于转速信号的变化， 在控制中引入了风速信号可以使变桨执行机构提前动作。

3.2 随机风速下控制性能仿真分析

采用IEC Kaimal 风速模型，在FAST 软件中生成轮毂高度平均风速为15 m/s 的风速数据（图4）。

图4 风速曲线Fig.4 Wind speed curve

在该风速下，针对3 种不同的控制策略，仿真得到风电机组桨距角和转速的响应曲线（图5）。

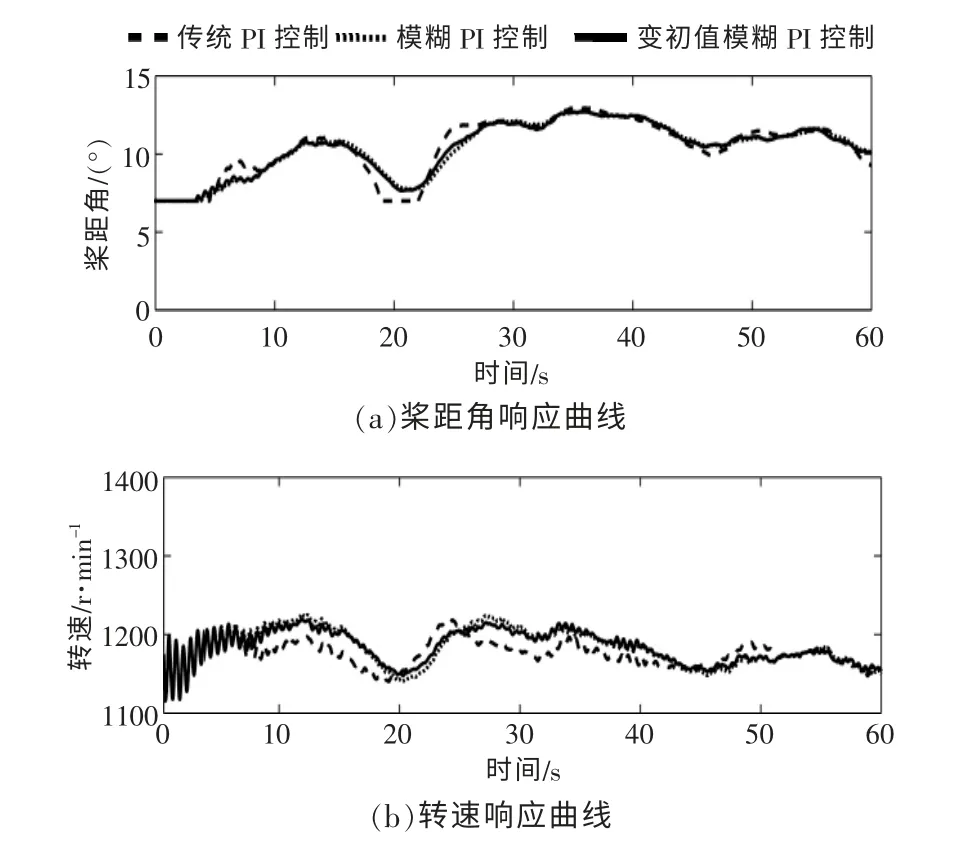
图5 桨距角和转速的响应曲线Fig.5 Comparison of pitch angle and speed response curves

由图5 可知： 根据统计分析， 变初值模糊PI控制的桨距角变化更平滑，标准方差为1.64，而传统PI 控制的桨距角变化的标准方差为1.78，模糊PI 控制的桨距角变化的标准方差为1.67；对转速的波动来说，变初值模糊PI 控制的方差为20.51，相比模糊PI 控制的23.4 下降了12%。 相比于传统PI 控制和模糊PI 控制， 本文提出的变初值模糊PI 控制具有明显的优势。

由于桨距角的变化会影响风电机组叶片和塔筒的受力，因此，本文也比较了3 种不同控制策略下的叶片和塔筒的受力力矩。对塔筒和叶片来说，力矩的波动越小越好。 力矩的大幅度波动不仅会影响机组的寿命，更会影响机组运行的安全。 图6为叶片和塔筒在迎风方向上的受力力矩曲线。

图6 叶片和塔筒受力曲线对比Fig.6 Comparison of blade and tower tube force curves

由图6 可知： 针对叶片根部的受力力矩数据， 在变初值模糊PI 控制下其变化波动的标准方差为1 266，相比模糊PI 控制下，其变化波动下降了2.5%， 相比传统PI 控制则下降了5.5%；针对塔基的受力力矩数据， 在变初值模糊PI 控制下，变化波动的标准方差为11 020，相比模糊PI 控制下变化波动下降了1%，相比传统PI 控制下降了6.3%。

4 结论

本文针对传统PI 控制器在控制非线性对象时鲁棒性差的问题， 提出了一种基于风速的变初值模糊PI 变桨控制算法，并从转速、叶片和塔基受力力矩波动的控制效果说明了该算法的优势，得到以下结论。

①分析了不同风速下变桨控制器对应的最优初值， 并通过曲线拟合的方法得到了变初值模糊PI 控制算法，实现了变桨PI 控制器参数的自适应调节，在变桨控制中引入了风速信号，能够使变桨机构提前动作。

②采用FAST 软件中多自由度非线性风机模型， 从抑制叶片和塔基受力力矩波动方面验证了本文提出的控制算法的优势。