美国AAR与LMA车轮踏面在CHN60上的动力学对比分析
邓会栓,殷玉枫,谢春风,高崇仁
(太原科技大学机械工程学院,太原030024)
近年来,随着我国经济的飞速发展,我国的高速铁路事业也取得了令世人骄傲的成绩,特别是我国高速铁路实施的“走出去”战略,中国高铁在国外市场越来越受欢迎,高铁作为中国走向世界的明信片已经相继走入欧、亚、非等国际市场。尤其是近几年国家“一带一路”战略的提出和实施,为我国高速铁路的快速发展和走向海外提供了更为有利的契机。然而由于每个国家不同的铁路标准,火车车轮踏面也各不相同。因此在与国外高铁合作项目中,会遇到由于轮轨匹配关系带来的诸多问题。因此,研究不同车轮踏面的动力学性能对于我国高速铁路的飞速发展具有十分重要的战略意义。尤其是随着不断提高的高速铁路车辆速度,对于车轮与轨道之间的匹配关系要求也越来越高。
车辆的动力学性能主要包括平稳性、安全性和车辆曲线通过能力三个方面。机车在运行过程中会受到轨道不平顺、线路不平顺、轨道曲线半径不标准、车辆或者机器装备自身所产生的激励、驱动以及制动时相邻两个车厢之间的相互作用力等方面的影响,这样对于车辆的平稳性的要求是非常不利的,使乘客乘坐车辆的舒适性降低;仿真车辆的安全性以及车辆的曲线通过能力所常用的动力学指标有车辆的脱轨系数、轮轨之间的作用力以及轮轴的横向力等参数。研究车轮踏面的主要的动力学性能对于未来中国铁路技术在世界上的地位是十分重要的。
本文应用专业的铁路分析软件SIMPACK分别建立了LMA和美国AAR两种车轮踏面车辆,在同一条件下去做仿真,对比分析两种踏面的车辆运行时的主要动力学性能:车辆运行时的平稳性、安全性以及车辆运行时通过曲线能力的能力。
1 模型的建立
SIMPACK多体动力学分析软件是德国INTEC Gmbh公司针对机电、机械系统运动学、动力学做仿真分析而开发的多体动力学分析软件包。SIMPACK轮轨模块是SIMPACK软件中的一个专业模块,包含了铁路行业全部相关的动力学分析,是非常专业的铁路仿真软件[1]。
1.1 轮轨踏面模型
1.1.1 LMA踏面
LMA型车轮踏面[2]是我国自主设计磨耗型车轮踏面,目前LMA型车轮踏面目前广泛应用于CRH1、CRH2、CRH3高速动车组上,其基本尺寸如图1所示:

图1 LMA车轮踏面外形
1.1.2 AAR型踏面
AAR型车轮踏面[3]是美国的宽车轮踏面模型,是目前美国应用的踏面模型,其基本尺寸如图2所示:

图2 AAR车轮踏面模型
1.1.3 踏面的形成
应用AutoCAD软件实现LMA和AAR两种车轮踏面的数值离散化,编写成SIMPACK能识别的.prr格式来进行轮轨外形的拟合。
1.2 钢轨模型的建立
建立的钢轨是目前高铁用的最多的CHN60钢轨,其中钢轨的横截面是工字型,由轨头、轨腰和轨底等主要部件组成。它是按照车辆运行后,钢轨磨损后的形状设计的,其主要尺寸如图3所示:

图3 CHN60钢轨外形
轨道不平顺是车辆在运行过程中产生振动以及动力学的主要原因,描述的是车辆随机产生振动的特性,因为是随机产生的,所以很难用具体的函数来进行表达,一般选择功率谱密度来进行表达,相对来说,美国和德国在轨道谱的研究上比较成熟,所以在仿真中选择了德国的低干扰谱来作为轨道不平顺的模型。

图4 德国低干扰谱
在曲线通过能力和脱轨性分析时,本次所采用的线路几何模型:半径为800 m的曲线,其中200 m为直线,100 m为缓和曲线,150 m为圆曲线,70 mm为超高,车速为200 km/h.
1.3 车辆模型的建立
设置的车辆模型的质量、转动惯量以及外形结构尺寸,运用SIMPACK软件建立输入函数、力元、铰接和约束等,车辆模型如图5所示:

图5 车辆模型
2 曲线通过能力
车辆的曲线通过性能指的是车辆以一定的速度通过带有激励的曲线路线,然后分析车辆的轮轨接触力。由于车辆在高速运行过程中会导致轮轨之间在作用力急剧增大,加剧了钢轨、扣件、枕轨等部件之间的破坏程度,因此需要严格的控制高速铁路轮轨之间的作用力。主要是分析轮轨之间的横向力和轮轨之间的垂向力。
2.1 轮轨之间的垂向力
日本在既有线提速试验中,对车轮重量做出了非常明确的规定:轮轮重量最大值必须小于轨道部件的设计载荷,一般情况下,轮重的设计载荷是静载荷的3倍[4]。
英国铁路规定了车辆通过钢轨接头等瞬间冲击作用时的轮轨垂向力P1、P2的限制标准,即
P1≤400 kN
(1)
P2≤250 kN
(2)
P1+P2≤600 kN
(3)
德国联邦铁路对于车辆力的规定:车辆的轮轨垂向力的极限值不能超过170 kN.我国颁布的《高速动车组整车试验规范》标准规定[5],车辆在运行过程中,轮轨垂向力的最大值不能超过170kN[5].
2.2 轮轨横向力
在铁路轨道上横向力不具有垂直方向上的强度,几乎都是依靠经验来定横向强度的值。当车辆线路是不良的状态时,车辆就会因为轮轨横向力的过大而导致轨道和扣件的损坏,严重时会导致脱轨现象的发生。因此对于轮轨横向力的大小,不同轨道有不同的限定标准:木枕受到道钉所承受的横向力的限制;高速铁路由钢轨弹性和扣件的设计载荷来确定。日本对轮轨横向力的极限方面做出的研究[6],如表1所示:

表1 JR道钉挤压及拔起时横向力限定标准
如表1所示,第一限度为理论上不能超过的值,第二限度是在现实中采取相应措施的极限值。
欧美和日本一般取0.4倍轴重作为横向力的允许限度,即:
Q≤0.4(Pst1+Pst2)
其中,Pst1——左轮静载荷(kN)
Pst2——右轮静载荷(kN)
我国的高速铁路基本上都采用弹性扣件的轨道,因此,轮轨横向力不能超过钢轨弹性和扣件的设计载荷,参考欧美标准。
2.3 AAR和LMA踏面车轮的左右横向力
在图6、图7中,实线表示右轮的横向力,虚线表示左轮的横向力。当车辆以200 km/h行驶时,两种车轮踏面的车辆的横向力相差不大,没有超过表1中的第一限度值和道钉拔起横向力的值,满足轮轨横向力的设计标准。

图6 AAR车轮横向力

图7 LMA车轮横向力
两种踏面的车辆在轨道上受到的激励是相同的,因此在车辆行驶过程中受到的轮轨横向力也不会相差很大。
2.4 AAR和LMA踏面的轮轨垂向力

图8 AAR左右垂向力

图9 LMA左右垂向力
在图8、图9中,虚线表示右轮的垂向力,实线表示左轮的垂向力。当车辆以200 km/h行驶时,由图所知,两种车轮踏面右轮受到的垂向力最大,并且两者的变化规律基本上是一致的。当车轮垂向力达到最大值为55 kN时,也都远远小于我国的最低标准值170 kN,所以在考虑车轮踏面垂向力时,AAR踏面车轮的车辆的运行安全是完全符合条件的。
3 脱轨性能的定义
车辆在运行过程中,会受到车辆自身以及轨道不平顺等各种因素的影响可能使车辆发生脱轨的现象。车辆的脱轨性用脱轨系数来表示,脱轨系数的大小决定这脱轨可能性的大小,脱轨系数越大则表示铁路车辆脱轨的可能性也就越大。脱轨系数是用来评价车轮脱轨稳定性能的指标,它指的是在某一时间作用在车辆车轮上的横向力与垂直力之间的比值(Q/P)。车轮上横向力和垂向力的选取规则:假设车轮和钢轨接触点位于轮对中心线垂直平面内,分析车轮与轨道接触的具体受力情况,从而得到车轮脱轨时临界状态的受力分析示意图,如图10所示。
由图10中各个作用力分别向轮轨接触点A的切线方向和发现方向投影后,得到的关系式:
N=Pcosα+Qsinα
(4)
T=Psinα-Qcosα
(5)
由上述两式联立得:
(6)
其中,Q——轮缘上的横向力;
P——车轮上的垂向力;
N——钢轨对车轮的法向反力;
T——钢轨对车轮的切向反力;
α——车轮轮缘角。

图10 车轮脱轨临界状态作用力关系
在车轮的不断运行过程中,车轮与轨道之间会产生“儒滑力”,理论上来说,“儒滑力”的大小不超过车轮与轨道之间的摩擦力μN。通过式(6)可以获得Q/P的值,切向力T达到摩擦力μN时取最小值,即在此极限状态下,T=μN,和式(6)联立可以得到脱轨系数的临界值为:
(7)
由式子(7)可知,脱轨系数的大小与轮缘角α和轮轨之间的摩擦系数μ有直接的关系。
我们国家出台的《铁道车辆动力学性能评定和试验鉴定规范》(GB5599-85)标准规定[7],为了防止脱轨事故的发生,铁路车辆的脱轨系数应当满足的条件条件为:
同时,根据国际铁路联盟UIC标准,铁路车辆的脱轨安全值为Q/P≤1.2.
我国铁路行业标准《铁道机车动力学性能试验鉴定方法及评定标准》(TB/T2360-93)[8]规定的机车脱轨系数界限值如表2所示。

表2 我国TB/T2360-93规定的机车脱轨系数界限值
3.1 LMA踏面和AAR踏面的车辆以200 km/h通过曲线时的仿真结果
不同踏面的轮对与钢轨接触形成不同的轮对接触关系,从而得到他们不同的脱轨性能,两种车轮踏面的脱轨系数图分别如图11、图12所示。

图11 AAR车轮脱轨系数图

图12 LMA车轮脱轨系数图
在图11和图12两个图中,实线表示铁路车辆右侧车轮的脱轨系数,虚线表示铁路车辆左侧车轮的脱轨系数。
由以上两个图可知:
(1)当车辆以200 km/h的速度通过圆弧曲线时,LMA踏面的车轮和AAR踏面的车辆的脱轨系数相差还是很大的,LMA踏面的车辆的左右脱轨系数都小于0.6,根据我国铁路行业标准对车辆的评价等级属于优这个级别,AAR踏面的车轮在整体上还是好的,根据我们国家出台的《铁道机车动力学性能试验鉴定方法及评价标准》来看,两种车轮踏面的车辆都在合格的范围,属于允许的限度,也符合国际铁路欧盟的标准。
(2)当轮对通过缓和曲线时,LMA踏面车轮的脱轨系数达到最大值,而AAR踏面的车轮则不然。
(3)两种踏面产生的脱轨系数不同原因:之所以两种车轮踏面差距这么大,主要和车轮踏面的外形有关,当车辆在弯曲的轨道轨道上行驶时,由于超高曲线的定义,车轮踏面会发生横向位移。由图1可知,LMA踏面的车轮在主要的接触面上有两个圆弧,当车轮发生横向位移时,左右轮都能和CHN60钢轨良好的匹配;而由图2可知,AAR踏面的车轮当车辆进去弯曲轨道时,由于踏面是一段1:20的斜度直线而不是LMA踏面的圆弧曲线,因此和CHN60车轮踏面匹配关系不是很好,会造成车轮横向力的增加,从而导致左侧车轮的脱轨系数增大,同时也会造成车轮踏面和钢轨的严重磨损。
4 舒适性
铁路车辆的运行平稳性反映的主要是车辆的振动程度。铁路车辆在轨道上运行时,车辆会产生各种各样的振动,包括车辆自身的振动以及各个部件的振动等都会影响乘客的舒适度。当乘客一直置身于振动的环境中时,不仅会使人产生疲劳感,还会使人体的内部的各个器官以及各个组织和车辆振动发生谐振[9-11],从而对人的身体造成严重的伤害。
评价旅客乘坐铁路车辆舒适性最直接的指标就是车辆在轨道上运动时,车体自身振动的加速度.为了更加精确评价乘客的舒适度,不仅要把铁路车辆轨道上运行时,车辆振动加速度大小考虑在内,还要考虑车辆的振动频率。当考虑使用车体加速度评价乘客舒适度时,每个国家都有自己的标准。例如美国的Janeway指标、日本的舒适度系数、欧洲使用的Sperling指标等。其中从大量实验数据得到的欧洲使用的Sperling指标被国际广泛认可,可以用来作为评定车辆运行时舒适度等级。其中车辆平稳性指标W的公式为:
运行品质的评价公式:
舒适度的评价公式:
其中,上式中:
a——振动加速度(cm/s2)
F——振动频率(Hz)
F(f)——与振动频率相关的修正参数。
在实际车辆运行中,车辆振动是没有规律性的,所以车辆的频率和加速度也是随着时间而不断的变化的,也需要按频率对振动波形进行分组,统计每一组中振动频率的所有加速度值,可以得到车辆的平稳性指标公式:
一般情况下,Sperling的平稳性分为五个等级的指标,Sperling的舒适度分为四个等级的指标。但是在这两个之间又可以细化。平稳性等级用W值来评定,如表3所示

表3 车辆运行平稳性及舒适度指标与等级
我国在评定车辆运行稳定性时有时也会采用Sperling指标,但是相对于Sperling指标来说,我国对车辆运行平稳性指标等级又做了简化,对于三种不同的车辆,又划分了三个不同的等级,如表4所示。

表4 车辆运行平稳性指标与等级
4.1 舒适性分析模型
本次仿真模型所采用的路线为:10 000 m的直线轨道,铁路车辆的速度为200 km/h,车辆模型如图13所示:

图13 车辆模型
4.2 AAR和LMA踏面车辆横向和垂向平稳指标
由图14-图17可知,两种踏面车辆以200 km/h在直线线路上运行时,车辆在横向和垂向方向的舒适度都相差不大,在横向方向上,车辆平稳性的最大指标在0.4附近,在垂向方向上,车辆平稳性的最大指标也就是在0.6~0.7之间,比Sperling指标和我国独有的平稳性指标2.5小的多,乘客的舒适度会很好。
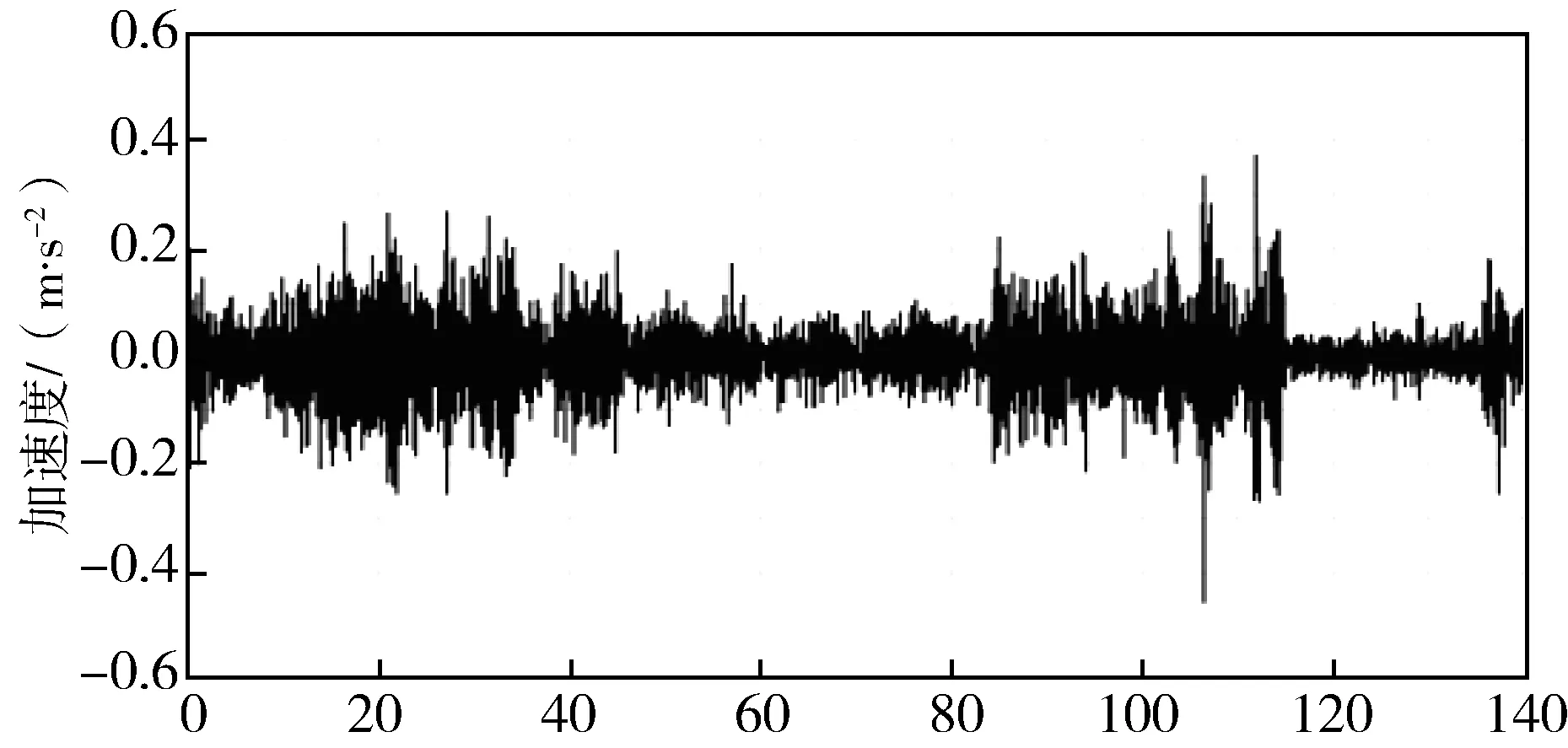
图14 AAR横向振动

图15 AAR垂向振动频率

图16 LMA横向振动频率
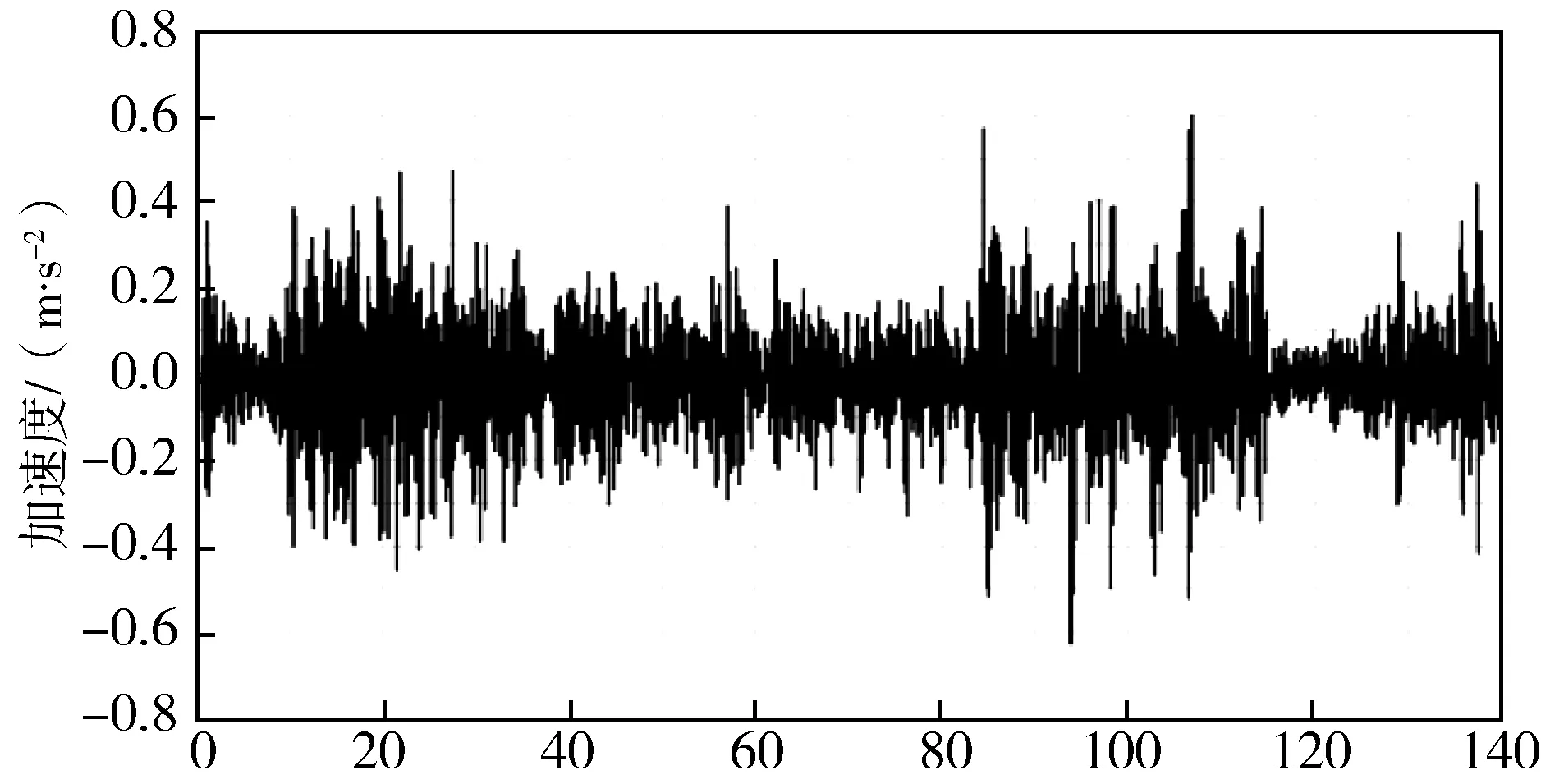
图17 LMA垂向振动频率
当铁路车辆在直线轨道上运行时,车轮不会出现横向移动的现象,所以这两种车轮踏面在直线上运行时,车辆的振动情况非常接近,两者的平稳性都满足要求。所以乘客不会长时间的感到不舒服。
5 结论
当不同的车轮踏面在轨道上运行时,两者性能有很大区别。当车辆通过曲线时,不同踏面车辆的横向和垂向轮轨力相差不大,都满足国家的标准;当考虑车辆的安全性能时,两者的差距还是比较大的,LMA踏面车轮的脱轨系数最大在0.6,而AAR踏面车轮的脱轨系数最大为1,虽然比国际的危险系数1.2小,但是出于安全性考虑,在考虑安全性问题时,踏面的设计应该考虑LMA踏面的参数;在考虑车辆运行时乘客的舒适性时,AAR车辆的横向振动小于LMA车辆的横向振动频率,在此方面考虑设计车轮踏面时,AAR参数可能更优。
通过对比分析车辆运行时的主要动力学性能,为以后设计不同车辆车轮踏面提供一个参考,更加有利于高铁国际化。

