基于改进狮群算法的主动配电网综合优化研究

张琼艺，刘立群，刘天保，刘春霞

(太原科技大学电子信息工程学院，太原 030024)

在主动配电网环境下，大量分布式电源并网，不仅对配电网潮流影响较大，还对系统的电能质量、损耗、可靠性等指标产生一定程度影响。如何在提升分布式电源消纳水平的前提下，实现对配电网的经济安全优化运行，具有重要的意义[1]。研究主动配电网的优化运行策略，在对可控分布式电源进行优化调度，不仅能够有效保障对可再生能源的消纳，还能够在保证电网供电的条件下最大限度提升配电网资产利用率并延缓投资改造进程[2]。

对于传统配电网来说，主要的系统优化措施通过网络结构重构与电容器配置优化来实现，不论是单一的优化措施还是多重优化措施，均取得了较好的优化效果，也形成了诸多研究成果[3-6]。随着主动配电网的研究进一步深入，对分布式电源的调度优化成为系统运行控制的重要对象。文献[7]提出了基于负荷控制的故障恢复重构策略，采用NSGA2算法进行了重构分析，给出了故障情况下的孤岛供电方案。文献[8]将分布式电源补偿与补偿电容器组投切作为统一的优化手段，以系统损耗以及电压偏移量最小为多目标，提出了包含自适应参数的多目标和声算法来求解最优的分布式电源出力与无功补偿容量。但两者均只是针对单一的配电网无功优化以及网络重构，并未涉及综合优化问题。文献[9]根据负荷变化问题，采取单调性初步分段方式对设备动作次数进行约束，将综合问题分解为网络重构与无功/电压优化控制两个单独问题，分别由精确矩法与粒子群优化算法交替求解。文献[10]基于无功优化策略对配电网的负面效应，排列了电容器无功补偿、变压器档位调整、分布式电源无功出力、网络结构调整等次序，形成了较为合理的主动配电网无功优化策略，但不足之处在于多目标权重系统选择主观性较突出。文献[11]构建了以无功优化、

分布式电源有功优化、网络重构为基础的综合优化运行模型，采用改进粒子群算法进行模型求解，以获取系统最佳运行方案，但编码方式效率仍有提升空间。文献[12]研究了可控调度机组参与的最优潮流运行调度问题，通过优化少环网的连枝上串联理想电压源于网络的近似等效变化方法，完成了重构、电容器投切、分布式电源出力的协同优化。

针对主动配电网的分布式电源接入问题，本文将配电网重构、电容器无功优化投切、分布式电源处理调整等进行组合编码，建立主动配电网综合优化数学模型，并提出改进的狮群算法进行模型优化求解。

1 主动配电网综合优化模型

根据主动配电网的经济运行目标，以系统有功损耗最小为目标来开展相应的综合优化分析，具体的数学表达式如式(1)所示。

(1)

Ploss为配电网的有功功率损耗，N为网络中的能够进行开断及联络的馈线开关总数，ki为开关i所处的状态，当该馈线开关处于断开时取值为0，该馈线开关闭合时取值为1；ri为馈线开关i所在线路的电阻；Pi为馈线开关i所在线路的有功功率，Qi为馈线开关i所在线路无功功率；|Vi|为馈线开关i所在线路末端节点电压幅值。进行综合优化时需要满足的约束条件有潮流方程、网络结构约束，以及线路带载、节点电压、分布式电源出力、补偿电容器容量等不等式约束。

对于配电网的安全可靠运行来说，不论分布式电源出力及无功补偿装置如何调整，系统结构如何变化，系统潮流应始终处于平衡状态，根据配电网的闭环设计、开环运行特点，在实施重构后必须满足辐射状供电结构要求，不能出现环网以及孤岛。

不等式约束如式(2)所示：

(2)

其中Si为馈线i上的视在功率，Simax为馈线i的视在功率限值，代表馈线段的带载限制，Nl为配电网中的馈线总数；Uimax、Uimin分别为负荷节点i的电压上下限范围，Nn为配电网中负荷节点总数；PDGi、PDGimax分别为第i处并网分布式电源的有功功率及有功功率最大值，QDGi、QDGimax分别为第i处并网分布式电源的无功功率及无功功率最大值；QCmin、QCmax分别为无功补偿电容的容量最小值与最大值。

目标函数以最小化为分析目标，为了更好地对应不同运行方式的优劣性，对目标函数进行适应度转换，同时对违反电压约束条件的个体进行惩罚处理，加入罚因子，适应度函数如式(3)所示。

(3)

上式中β为罚因子，Uimax、Uimin分别为节点i的电压上下限范围，ΔU为节点电压超出限定范围的具体偏差，其具体取值如式(4)所示：

(4)

2 改进的狮群算法

2.1 狮群算法原理及基本操作

群智能算法是智能优化方法的重要分支，通过模拟社会性昆虫及动物等群体的觅食行为，根据群体中个体信息交换及合作来实现对最终目标的搜索。典型的群智能算法有蚁群算法、人工鱼群算法、粒子群算法、萤火虫算法、蜂群算法、狼群算法等[13-15]。近年来，在对狮群捕猎行为特点分析的基础上，形成了全新的群智能算法——狮群算法，其全局收敛性能得到了有效验证并在实际工程中得到了较好的应用[16]。

在单个狮子群体中，主要由一定数量的雌狮、幼狮以及1只领头雄狮组成(更多情况下狮群中雄狮不止1只)，狮群的大小一般由栖息地块的食物状况来决定。雄狮游走范围决定了狮群栖息领地范围，而雌狮处于狮群的核心，是围捕食物的主要力量，幼狮的数量主要由领地中食物数量来进行控制。通过雌狮对猎物的包围，然后从各个方向向猎物靠拢，最终实现猎物获取。

在形成狮群算法时，食物源的位置代表着优化问题对应的一个可行解，位置优劣也就对应着具体的可行解个体适应度。幼狮、雌狮、雄狮在狮群中的数量按照比例进行分配，其中对应适应度较好的个体定义为雄狮，较差的定义为幼狮，其余部分定义为雌狮。

解的个数N等于全体狮子的个数。狮群算法随机生成含有N个解的初始种群，每个解xi用一个d维向量xi=(xi1,xi2,..,xid)来表示，d是待优化问题的维数。算法描述可由式(5)-(9)来表示：

(5)

xo(t+1)=(rand()-0.5)*r+xl(t)

(6)

xl(t+1)=xl(t)+rand()*(xl(t)-x(t))

l=1,2,…,nl

(7)

xs(t+1)=xs(t)+rand()*(xs(t)-xl(t))

s=1,2,…,ns

(8)

上式中ml为分布在第l只雄狮周围所聚集的幼狮数量，no、ns、nl分别代表着狮群中幼狮、雌狮、雄狮的数量，具体的数量在初始情况下按照给定的比例来分配。r为分布半径，rand()为随机数函数，代表[0,1]区间内的一个实数。xo(t)、xs(t)、xl(t)分别代表幼狮、雌狮、雄狮所处的位置，x(t)为狮群中随机选择的某个狮子所处位置。

针对给出的基本操作，狮群算法的核心原理可分为三个方面：一是幼狮分散在雄狮周围，主要完成算法的局部搜索；二是雌狮随机选择一个雄狮，瞄准雄狮位置并向其逐渐靠拢，进而完成一次自我的位置更新；三是在算法过程中，雄狮通过在领地范围内的随机游走，完成自我的位置更新。

2.2 基于免疫浓度选择的改进狮群算法

基本狮群算法虽然理论上能够实现全局收敛，但是由于算法结构简单、参数设置少等本质特征影响，在雌狮进行全局搜索过程中，对更新位置后的雄狮与雌狮个体主要通过竞标赛方法或者轮盘赌方法进行[17]，从而实现狮群的一次更新。该种做法在种群进化过程中，尤其是后期易造成个体高度集中，从而导致算法陷入局部收敛的不足。

本文根据人工免疫算法中浓度机制分析，通过个体浓度来进行复制选择，对于高浓度个体而言受到一定程度抑制，从而保证进化后期狮群始终处于一定的多样性，避免算法陷入局部最优。浓度选择采用基于矢量距的方法，首先用式(9)来表示个体适应度值f(xi)群体中的距离L(xi)[18]：

(9)

对于第i个个体的浓度Density(xi)，可用式(10)表示：

Density(xi)=

(10)

根据个体浓度，在执行选择操作时，按照式(11)计算出选择概率：

Ps(xi)=

(11)

根据上式可知，对于狮群种群而言，在进行一次进化操作过程后，雌狮、雄狮、幼狮个体位置均得到更新，与个体i信息相似的个体越多，则个体i被选择的概率就越小，相反，与个体i信息相似的个体越少，则其被选择的概率就越大。执行矢量距免疫浓度选择后，狮群中浓度过高个体得到有效抑制，但实质上适应值浓度较高的个体也能顺利进入到下一代狮群中，其优势在于能够使得含有部分优秀基因但整体适应度值较差的个体也能够进入到下一代种群中，狮群整体的多样性得到保证，从而避免过早陷入收敛。

2.3 改进狮群算法测试

为了验证本文所提的改进狮群算法的有效性，同时更好地对比算法的相关性能，选择文献[17]中的部分验证测试函数进行算法应用分析，分别采用基本狮群算法、粒子群算法、改进狮群算法进行函数仿真分析。对应的测试函数如式(12)所示，三个函数的全局最优值均为0.

(12)

针对三种算法的参数设置，基本狮群算法与改进狮群算法设置相同，狮群规模取值为50，狮群中雄狮、雌狮、幼狮的构成比例按照1:6:3来分配，分布半径为1，最大迭代代数为50代。粒子群算法中粒子群规模选择为50，学习因子C1与C2均取值为2，惯性权重系数采用照迭代搜索次数进行递减变化的方式[19]，惯性权重的最大值与最小值分别取为0.9、0.4.随机选择应用三种算法进行测试函数运算，将单次迭代搜索的收敛情况汇总如图1-图3所示。

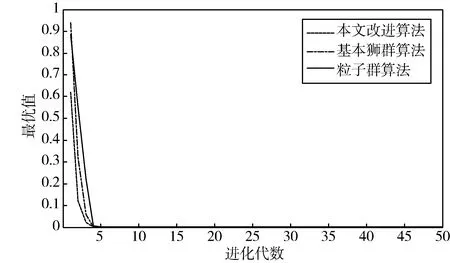
图1 函数f1(x)收敛结果

图2 函数f2(x)收敛结果

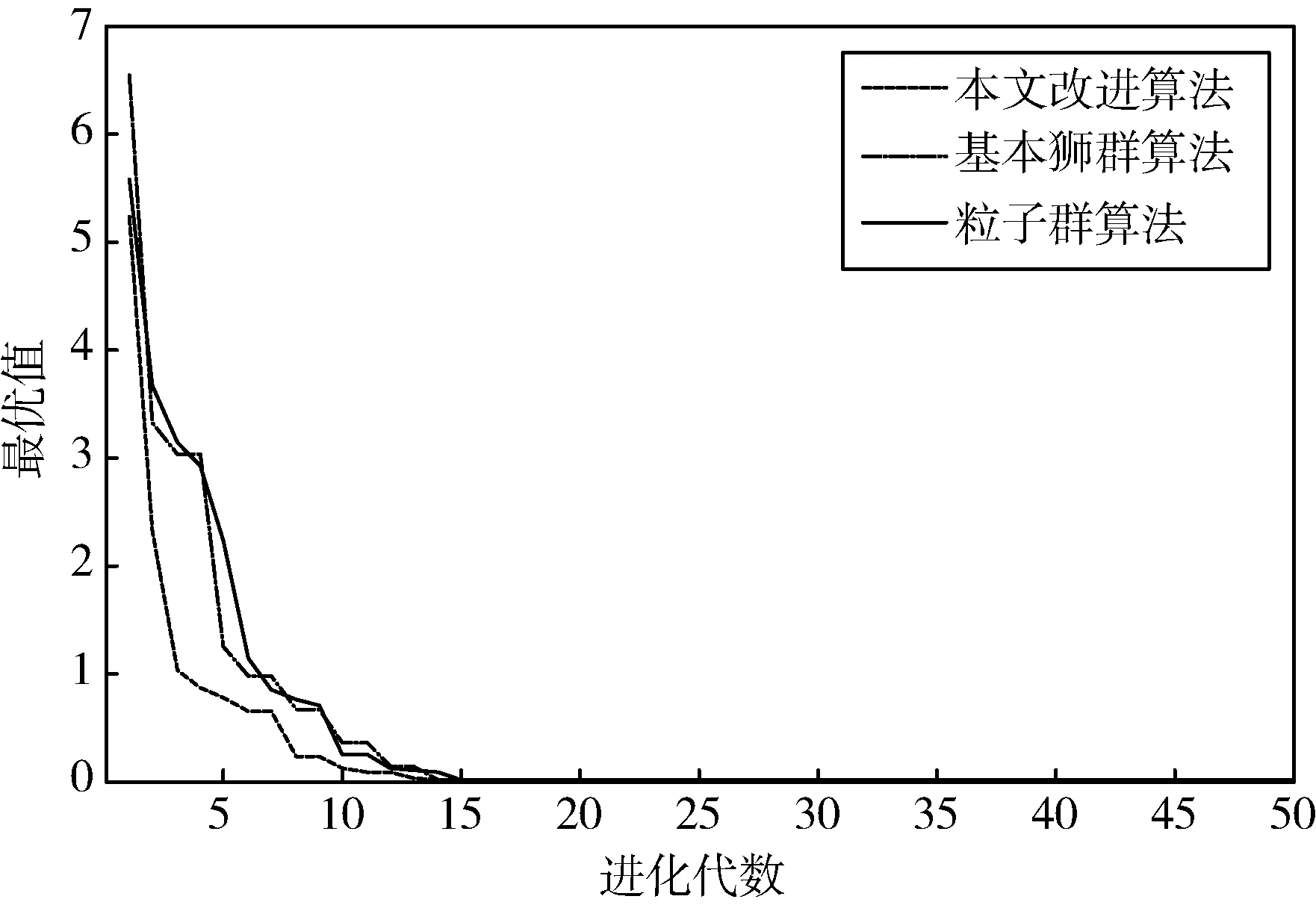
图3 函数f3(x)收敛结果

从图1-图3的收敛结果来看，本文的改进狮群算法均比基本狮群算法以及粒子群算法效果要好，最终得到的优化解处于全局最优解的极小范围内。选择针对函数f1(x)运行三种算法，将收敛代数的狮群中最优值、平均值汇总如表1所示。

表1 不同算法的搜索性能

从上表来看，改进狮群算法在第7次迭代时即寻找到最优解，而狮群算法以及粒子群算法所需的迭代次数均要多一些。根据狮群平均值的表现，由于迭代前期与迭代后期的量纲差距过大，无法在图中进行直观对比，表中给出的狮群平均值为收敛代数时狮群中个体的平均值。从该方面指标以及前述3个收敛图来看，由于改进算法中加入免疫选择操作，增强了狮群多样性，有效避免陷入局部最优的局面，能够取得较好的收敛性能。

3 基于改进狮群算法的综合优化

3.1 编码方法

在面对配电网综合优化应用时，交替迭代方法先进行配电网重构，然后在网络重构基础上进行无功优化，反复迭代操作直到优化结果无变化。其忽视了配电网重构与无功优化之间的内在联系，从而容易丢失全局最优的网络优化结构。为了在算法运用过程中得到较好的协同，本文选择将网络重构、电容器补偿、分布式电源出力控制三者进行组合编码的方式进行进化搜索。

针对粒子群子群与差分进化子群的特征，选用十进制实数编码，其中配电网重构部分的长度与网络中环路数量相同。对于无功补偿电容量来说，按组投切进行无功输出控制，在单组投切容量固定的情况下，其无功补偿容量本身就呈现出离散变化的特点。若单组投切电容器容量为C0时，补偿点i的电容器投切组数为Ci时，该补偿点处的总补偿容量QCi表达式如式(13)所示。

QCi=Ci×C0

(13)

为了将分布式电源与配电网联络开关进行组合编码，需要对分布式电源功率输出进行离散化处理。根据给定的分布式电源容量，设置一个功率步长λ，则容量的离散变量的取值范围应为(1，S/λ)的整数。构成的综合编码如式(14)所示：

[k1…ki…kNL|s1…sj…sMG|C1…Cl…CK]

(14)

针对解个体重构过程中随机选择联络开关断开易造成不可行解的情况，选择文献[19]中不可行解分析及处理办法。

3.2 分布式电源处理

而对于PI 节点、PV节点和PQ(V)节点的分布式电源来说，最终需要将非PQ节点转化为恒功率的节点进行迭代计算，为了简化计算，将分布式电源均看成是PQ节点来对待，在潮流计算过程中，将分布式电源节点等效成“负”的负荷节点[20]。

3.3 综合优化流程

在采用改进狮群算法进行主动配电网综合优化时，具体的步骤如下：

(1)狮群初始化，设定规模N，狮群比例等，读入配电网结构及参数；

(2)根据编码规则形成个体，按照给定比例分配雄狮、雌狮数量，根据式(5)计算分散在雄狮周围的幼狮数量；

(3)按照式(6)进行幼狮局部搜索，重新确定位置；

(4)按照式(7)、式(8)进行雄狮与雌狮位置更新；

(5)对更新后的雄狮雌狮位置与更新前的位置进行免疫浓度选择，组成新的狮群种群；

(6)找出当前狮群种群中的适应度最优个体；

(7)判断是否达到收敛条件，满足收敛则输出全局最优个体及其对应的运行方案，不满足则返回至步骤(2)，重新开始新的一次迭代进化。

针对前文提出的综合优化方案，其具体的实施步骤如图4所示。

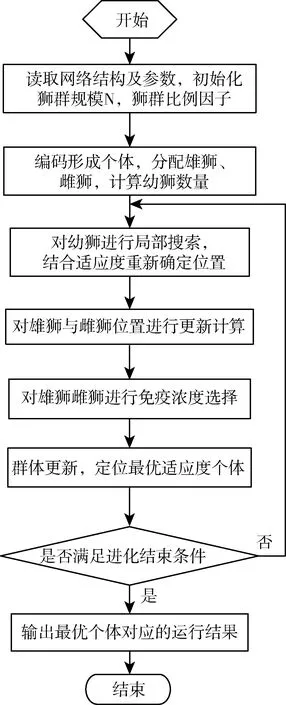
图4 综合优化流程图

4 算例分析

为了验证本文所提的改进狮群算法有效性，选择对IEEE 33节点系统进行验证分析，系统的初始数据来自文献[21]，包含33个节点，37条支路(联络支路5条)，总负荷为3 715 kW+j2 300 kVar，系统额定电压为12.66 kV，基准功率10 MVA.

为了体现分布式电源的接入，在系统内负荷节点4接入一组光伏发电机组、负荷节点31处接入一组风力发电机组，两处发电机组的有功功率输出上限为500 kW，无功输出范围为-100 kvar～300 kVar，在负荷节点15、27处分别接入无功补偿装置，补偿组数为10组，每组补偿容量为100 kVar，累计总容量上限为1 000 kVar，如图5所示。

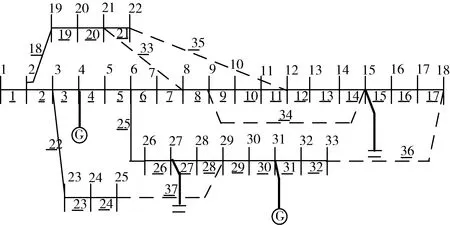
图5 改进的IEEE 33节点图

改进狮群算法中种群规模取值为50，个体编码维数为联络开关数量5，狮群中雄狮、雌狮、幼狮的构成比例按照1∶6∶3来分配，分布半径为1，最大迭代代数为100代。功率补偿λ为5 kW.在初始网络状态下，联络开关组合为8-21、9-15、12-22、18-33、25-29，系统损耗为203.06 kW，最低节点电压为负荷节点18处的0.913 0(标幺值)。将本文提出的改进狮群算法与基本狮群算法、粒子群算法进行综合优化对比分析，如表2所示。

表2 不同算法所得结果对比

从表2所给出的结果来看，分布式电源输出功率栏目中上层数据为并网点4处功率调度情况，下层数据为并网点31处功率调度情况；电容器投切栏目中上层数据为补偿点15处投切情况，下层数据为补偿点27处投切情况。基本狮群算法与粒子群算法均只能得到次优解，而本文改进狮群算法加入了免疫浓度选择操作，种群多样性得到保留，避免过早收敛到局部最优解，相应的优化目标值更优一些，在分布式最终得到的联络开关组合为8-21、14-15、9-10、17-18、24-25，系统损耗降低为62.587 kW，最低节点电压为0.951 6(标幺值)。

三种算法得到的优化结果中，虽然本文改进狮群算法最低节点电压指标要劣一些，主要是由于本文综合优化目标以系统网损最小为目标所致。对三种算法随机进行计算，记录群体中最优适应度值变化情况，统计如图6所示。从图中可看出，改进狮群算法具有良好的收敛性能，在第12代得到最优解，而基本狮群算法以及粒子群算法分别在第20代、24代取得次优解。将每一次迭代计算过程中的种群平均适应度值记录统计如图7所示，可看出，随着进化进程的推进，基本狮群算法与粒子群算法整个群体的平均适应度值处于逐步上升状态，在进化中期即使得种群陷入个体高度集中的单一局面。在结合免疫浓度选择的狮群算法下，经过初期搜索种群平均适应度上升，在中后期处于一个小范围内持续波动，种群多样性得到较好的保持，从而有效避免陷入局部最优的局面。

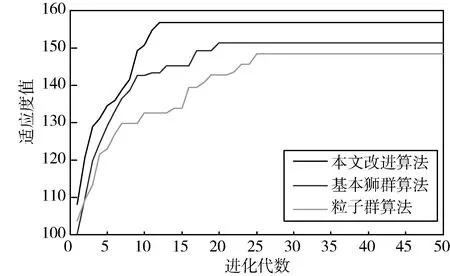
图6 单次计算群体收敛情况

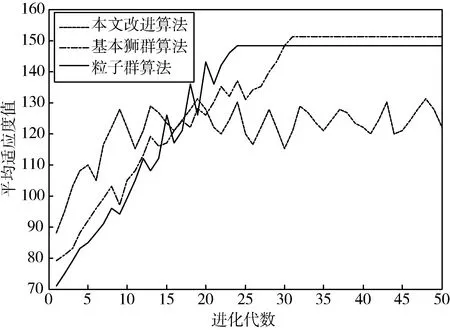
图7 群体平均适应度值变化情况

5 结论

在主动配电网环境下，可控分布式电源的并网运行对于配电网的经济安全运行带来较大影响，分析包含分布式电源出力控制时的综合优化运行具有较为重要的意义。提出了网络重构联络开关、电容器投切、分布式电源出力的组合编码，在群智能算法中基本狮群算法的基础上，根据轮盘赌选择易造成种群单一的不足，提出了基于免疫浓度选择的改进狮群算法。通过实际算例的综合优化分析，对狮群算法、粒子群算法、改进狮群算法进行了对比，结果显示改进算法的搜索效率以及种群多样性均较优，显示了其有效性与可行性。