基于优化的非等间距灰色模型对健康的预测

李 锐，李晓卉，李小钰，丁月民

(1.武汉科技大学信息科学与工程学院,湖北 武汉 430081； 2.华中科技大学同济医学院,湖北 武汉 430030；3.天津理工大学计算机科学与工程学院,天津 300384)

0 引 言

近年来，随着生活条件的提高，人们越来越重视自己和家人的健康问题，人们的思想也从最初的得病去医治转变为现在的以预防保健为主[1]。许多人不会在感到身体不适时才去医院治疗，而是越来越希望通过预测的方式来掌握自己或者家人的身体状况，以便提前做好应对措施，将意外风险降到最低[2]。因此，如何通过简单有效的方法实现对健康指标的预测便尤为重要[3]。对于健康预测，随着近年来的科技发展，学者们研究出许多类型的预测方案，有借助于大数据和云计算进行健康预测[4-5]；也有通过分析被监护者某些特别的健康指标是否异常来预测重大疾病发生的概率[6]；还有借助行为学来预测人们的健康情况[7]。然而，这些方法应用起来比较复杂且有相对严格的应用条件。在现实情况中，人们有时只搜集到某项健康指标的短期数据，并且这些短期数据很可能还不是等时间间隔的，若人们需要通过短期的不等时间间隔的有限数据来相对准确预测未来的健康情况，则会有一定的难度。

部分学者采用灰色一阶一元预测模型GM(1,1)来进行健康情况预测[8-9]。灰色预测模型具有样本数量要求低、原理简单、算法相对简便[10-11]、短期预测精度高、可进行检验等优点[12-15]。部分模型经过优化具有更高的精度，例如，舒服华等[16]是在灰色预测模型的基础上通过马尔科夫模型进行修正提高预测精度，然而，其是在等时间间隔数据的基础上进行预测的，即在利用传统的灰色预测模型进行预测时，其数据必须是等时间间距的数据[17]，如何找出最佳预测模型预测非等间隔的数据还需要进一步的研究。为解决采集数据时间不等间隔的问题，何敏藩等[18]采用了一种非等间距权重灰色预测模型来进行预测，实验表明其提出的模型具有有效性和可行性。为了进一步提高精度，许多学者还对非等间距灰色预测模型进行了优化，池其才等[19]是在此模型的基础之上对序列的初始条件进行二次优化；周春霖等[20]设计了一种非等间隔灰色预测模型，其是在灰色预测模型的基础上增加傅里叶残差修正以提高预测精度，然而此模型并没有寻找出非等间隔模型的最优权重系数，故还需要进一步优化模型。而在实际的健康预测中，一方面要考虑到采集到的原始健康数据可能会出现偏差和新加入的健康数据可能会发生突变；另一方面还要考虑到健康数据在一定范围波动的规律性和偶然性。因此，本文设计一种基于优化的非等间距灰色马尔科夫模型用于对健康指标的预测。在本文模型中，首先对原始数据进行预处理,优化预测流程并构建非等间距灰色预测模型；然后，设计非等间距灰色预测模型的最佳权重系数来优化模型；最后在得到预测结果后，考虑到预测残差的平滑性与随机性，采用灰色和马尔科夫修正相结合的策略对残差进行修正，从而使预测结果具有更高的精度。

1 模型构建

在使用模型进行预测时，预测的是数据发展变化的一种趋势，但若健康数据出现突变的现象，就会很大程度影响预测结果。为了提高预测的准确性，本文对原始数据进行预校检处理。若数据提供者的某项健康并无明显大的异常，则通常采集到的生理指标都是在一个正常范围之内。如果在对数据校检过程中，存在其中一个数据值突然偏离正常范围，而其前后数据都处在正常范围之内，即可认为此健康数据发生突变。若检测出数据突变，需要剔除突变数据，这样可以降低中间数据突变给预测结果造成的影响。

本文采用莱特检验法[21]对数据进行预校检，设由原始健康数据构成的m维时间序列x(0)=(x(0)(1),x(0)(2),x(0)(3),…,x(0)(m))，记录序列中每一个数据产生的时间t。

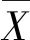
(1)

即认为x(0)(k)发生突变，需要将其剔除。式(1)中v为预检阈值倍数，根据不同生理指标其值也不同，通常设为1.5～3。若健康指标在正常健康范围波动越小，其值也越小。作预测之前，需与医学工作者根据不同健康指标及不同被监护人确定其数值。

对数列进行预校检剔除突变数据后即可得到新的n+1维时间序列X(0)=(X(0)(t1),X(0)(t2),…,X(0)(tn),X(0)(tn+1))。

序列X(0)中第k级与第k-1级的时间分别为tk和tk-1，则两者的时间间距为Δtk=tk-tk-1,，k=2，…,n。令Δt1=1。

接下来，需要构建累加数列。使用传统的非等间距灰色预测模型对X(0)构建累加数列如式(2):

X(1)(tk)=X(1)(tk-1)+X(0)(tk)Δtk

(2)

然而，通过实验验证，这样的方式并不能取得最佳的预测结果。原因在于健康指标并不一定会随着时间差变大而剧烈变动，因此在式(2)构建累加数列时将权重全部放在X(0)(tk)Δtk数据上必然会对预测造成偏差。

故可引入权重系数w，通过分配w的值可使累加数据更加平滑，如公式(3)：

(3)

对于最优的w值的确定，可以通过设定不同的w值构建模型，再通过各模型进行预测，预测结果精度最高的模型对应的w的值一般即最优值[13]。本文设计一种步进残差平方和寻优法来确定最佳权重系数，即令w=[0,0.5]，w初始值为0，步长为0.05，然后将w代入公式不断利用本模型做预测求得拟合值，若求得拟合值与实际值之差的平方和最小，则其对应的w值即为最优w值。即：

wbest=wmin={w1,…,wn}

(4)

另外，本模型在预测时，为保证预测的准确性，会不断将最新采集的数据加入到预测序列中。由于最新数据为最后一个序列，无法采用本文的莱特检验法判断是否为真的数据突变。为降低最新数据突变给预测结果造成的影响和保证预测数据起到预警作用，模型采用二次预测的方法对数据进行拟合，即：若样本有n+1个样本点，先取序列的前n个数据进行第一次预测；然后，再选取序列后n个数据进行第二次预测;最后,将二次预测的结果取平均值，作为最终的预测结果。

故对n+1维时间序列X(0)取其前n个数据累加，得到时间序列X(1)=(X(1)(t1),X(1)(t2),…,X(1)(tn))。

对X(1)建立灰色模型的一次微分方程，其方程如式(5)：

(5)

其中，α和μ为待定系数，α表示发展灰数，μ表示内生控制灰数。

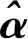
(6)

其中，Yn和B的计算分别如式(7)和式(8)：

(7)

(8)

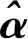
(9)

(10)

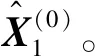
2 马尔科夫残差修正与模型检验

经过第1章的模型预测，可以得到健康指标残差数列，由于健康指标的残差具有规律性和随机性，因此为了提高预测结果的精度，本文采用灰色与马尔科夫相结合的方法对残差进行修正。

2.1 残差修正

根据第1章介绍的非等间距灰色预测模型特性可知，其对于小样本、非等间隔的和数值差不是太大的数据有较好的预测作用，而残差数列同样符合这样的特征，因此通过公式(11)取得残差数列之后，对其取绝对值进行一次本模型修正。在得到残差序列预测值后，再将其值还原到最终的预测结果当中，并在还原时，保证残差序列的正负号不变。

(11)

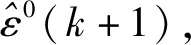
首先按照合适的标准将残差序列ε0划分为z种状态M=(M1,M2,…,Mz)。那么第f步的状态转移概率为：

(12)

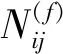
然后可得到状态转移矩阵为：

(13)

设各个状态区间首尾端的平均值为Ci，设通过f步转移预测，则模型会生成f个转移概率向量，预测未来时刻各状态的概率即为这f个概率向量的和。接下来从向量和中统计出各状态频数，即可得到残差修正预测值：

(14)

其中，xi为处于Mi状态的个数，Ci为Mi状态的中心值。

此时将马尔科夫预测值与灰色预测值取均值，即可得到最终的残差预测值，如式(15)：

(15)

最后将原始预测值与残差值相加，可得到经修正后的最终预测结果为：

(16)

2.2 模型检验

预测结果得到之后，需要检验模型的合理性，常用的检验方法有相对误差检验法、关联度检验法以及后验差检验法。相对误差检验法仅可检验预测结果偏差的多少，并未考虑预测结果的离散程度；关联度检验法通过计算关联系数来判断预测序列曲线与建模序列曲线的相似度，不能直观地看出检验结果精度等级。综合考虑，本文采用后验差检验法对组合预测模型进行精度检验，判定模型是否合理。

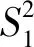
(17)

小误差概率p为：

(18)

本模型的精度由指标C、p共同划定，一般的模型级别取max{C的级别，p的级别}，精度参照表如表1所示。

表1 精度参照表

3 应用实例与分析

本文以某医院被监护者的胎心率为例，用优化的非等间距灰色预测模型来预测未来一段时间的胎心率情况。胎心率情况见表2，其中已怀孕天数为D，所测胎心率实际值为T。

表2 胎心率数据

由此可得到初始时间序列X(0)=(119, 135, 82, 125, 132, 136, 128, 132)，从医务工作者得到预检阈值倍数v为2.2，通过预校检得到新的时间序列X(0)=(119, 135, 125, 132, 136, 128, 132)。

先取前6个数据作预测，则X(0)=(119, 135, 125, 132, 136, 128)。借助本文模型，采用本文提出的步进残差平方和寻优法可以确定最优权重系数w，图1为第一次预测中采用不同权重系数预测得到的相应平方和值，从图1可知，最优权重系数w为0.3。

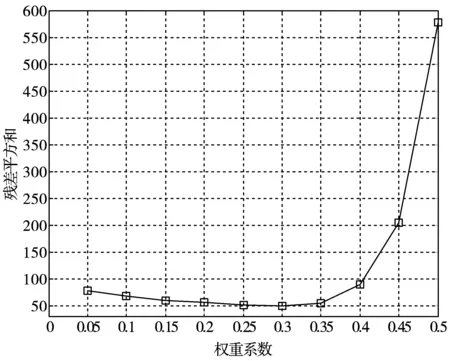
图1 第一次预测的步进残差平方和

则根据最优权重系数可得到拟合值以及预测出第81天及第83天的胎心率值为：

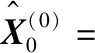
再取后6个数据X(0)=(135, 125, 132, 136, 128, 132)做步进残差平方和求最优权重系数，如图2所示。

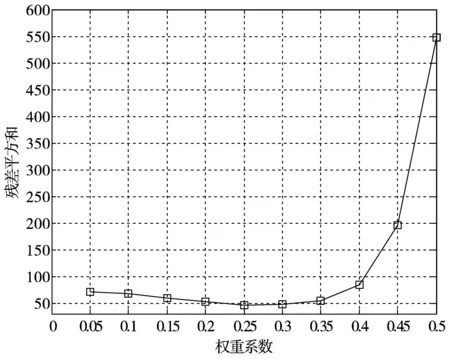
图2 第二次预测的步进残差平方和

可知最优权重系数w为0.25，则根据最优权重系数可得到拟合值以及预测出第83天的胎心率值为：

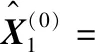
两组结果求平均值可得各天数胎心率的拟合值，如表3所示。其中拟合值以P表示，误差率以R表示。预测未来第83天的值为132.4。

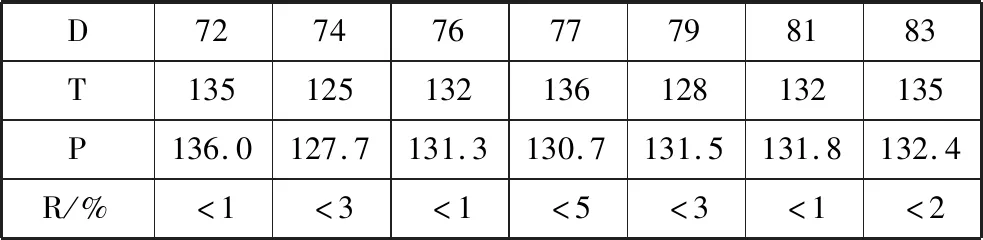
表3 胎心率修正前预测结果

为了进一步提高精度，对残差序列进行修正。先求出残差数列：

ε0=(-1.0, -2.7, 0.7, 5.3, -3.5, 0.2)

取绝对值，通过本GM(1,1)模型可得：

接下来进行马尔科夫修正，对残差序列ε0划分为3种状态M=(M1,M2,M3)，各状态值分别为[-3.5,-0.6]、[-0.6,2.4]、[2.4,5.3]。

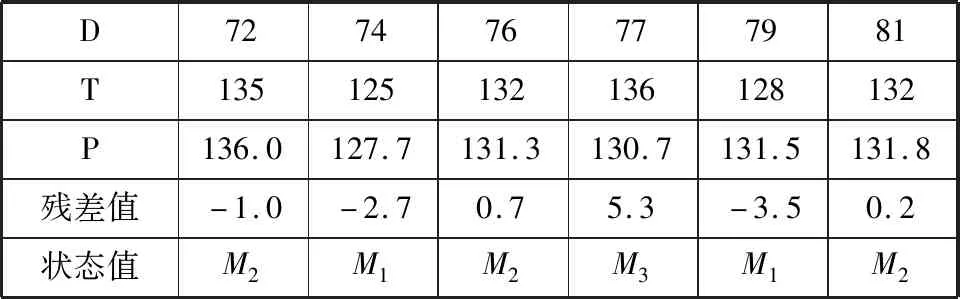
表4 残差序列预测状态表

则状态转移矩阵为：

根据状态转移矩阵，得出下一时间的状态转移概率表，如表5所示。

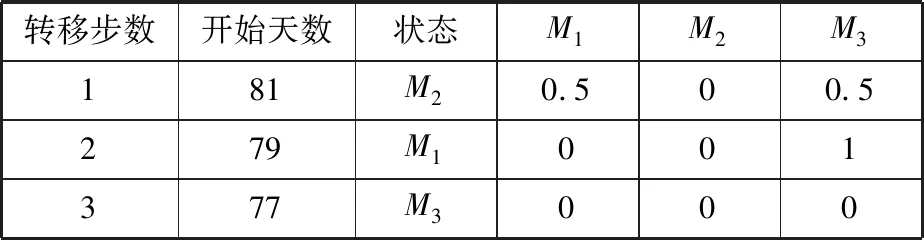
表5 下一时刻的状态转移概率表

根据各状态中心值C1=-2.1，C2=0.9，C3=3.9，可求得由马尔科夫预测的下一时刻的残差值：

根据公式(15)，可得到下一时刻的最终的残差预测值：

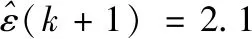
再由公式(16)将残差值与预测值相加得到最终第83天的预测值：

所有修正后的结果如表6所示。

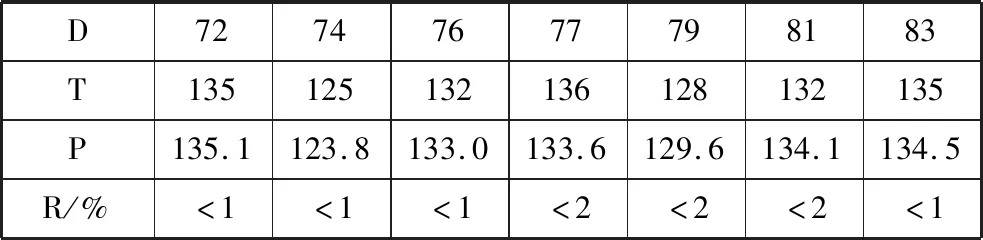
表6 经灰色马尔科夫残差修正后的预测结果

至此预测结束，经残差检验C=0.171，p=1，根据精度可知，本文预测模型后验差比C和小误差概率p这2个指标均在一级模型精度范围内，故精度等级检验为一级。因此，预测得到的第83天的胎心率具有较好的准确性，可以给被监护者带来有益的参考。

不考虑数据突变，分别采用传统非等间距GM(1,1)模型、文献[20]提出的单一因子优化模型和本文模型对胎心率情况作预测，得出的各模型数据拟合值如图3所示。从图3可看出，本文设计的预测方法具有更高的准确性。

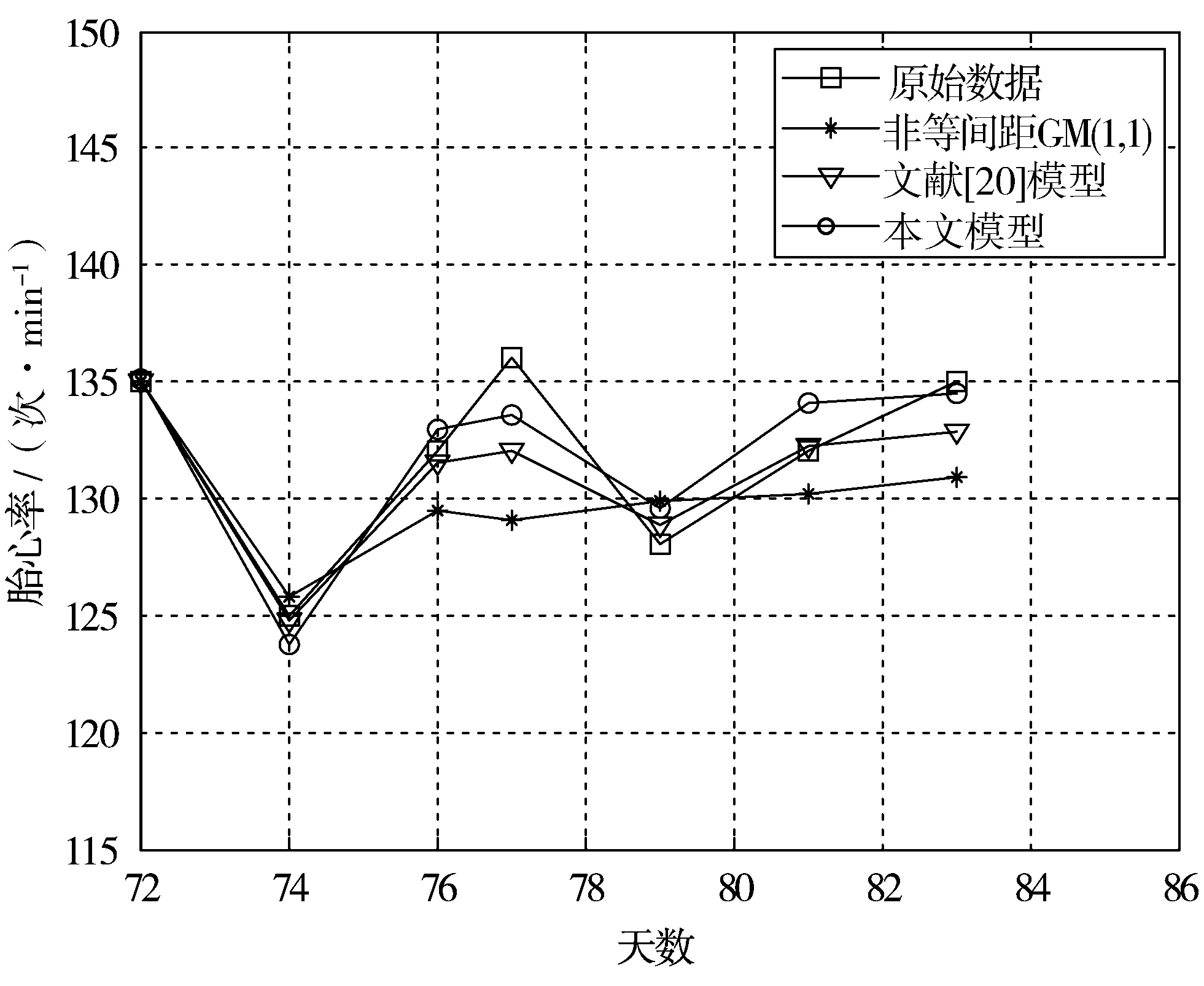
图3 3种预测模型对比图

表7为3种模型的后验差比C和平均相对误差E的值，从中也可看到，本文的预测模型具有更好的精度。

表7 3种模型后验差比C和平均相对误差E对比

4 结束语

本文提出了一种利用优化的非等间距灰色马尔科夫预测模型预测被监护者未来健康指标的方法。该方法在构建模型时采用对初始数据进行预校检和多次预测的策略降低了数据突变对预测结果的影响，并在非等间距灰色预测模型基础上设计了最佳权重系数来优化预测模型；另外为了进一步提高预测精度，在得到结果之后，本文采用灰色和马尔科夫相结合的策略进行残差修正。实例分析表明，该预测方法对预测短期健康指标情况比较准确，平均相对误差为1.037%，比传统的非等间距模型总体平均相对误差低约0.9个百分点，比单一的优化策略预测模型总体平均相对误差低约0.6个百分点，故能更好地帮助人们进行健康预测和管理。