云计算环境下的可修分布式系统可靠性分析方法

杨牧川，吕晓丹，蒋朝惠,2

(1.贵州大学计算机科学与技术学院,贵州 贵阳 550025； 2.贵州省公共大数据重点实验室,贵州 贵阳 550025)

0 引 言

分布式系统、集群计算和网格计算等技术是支撑云计算技术发展的关键技术[1]。随着用户数量的不断增加，数据中心的规模在迅速扩大，同时其架构变得日益复杂，导致云计算系统的运行故障频繁发生，造成了巨大的损失。因此，在规模巨大、架构复杂的云计算系统中，如何保障系统的可靠性已经成为一个极具挑战性的问题[2]。

目前，各种分布式系统在云计算平台中处于核心的地位。有基于MHA和Galera的数据库集群[3]，HDFS、Ceph、Swift等分布式存储系统；RabbitMQ、Kafka等分布式的高级消息队列协议实例；以及由httpd、nginx、haproxy、Varnish、Redis等技术构建的负载均衡和缓存集群。此外，还有确保各个服务高可用的corosync/pacemaker和keepalived高可用集群。因此，云计算平台的可靠性很大程度上取决于这些分布式系统的可靠性。

随着电子政务、电子商务、多媒体服务等进一步云化，这就要求系统故障在被用户感知之前得以预测和消除[4]。而现有针对云计算平台这样的含有大量可修分布式系统的研究大都是关于可靠性优化的调度算法和调度策略，缺乏对分布式系统可靠性本身的分析方法[5]，因而不能定量地衡量系统可靠性的高低。所以，研究可修分布式系统的可靠性分析方法是十分必要的。

1 相关研究

由于云计算平台大都是由大量廉价易失效的x86体系架构的服务器组成[6]，这些服务器构成的分布式系统中的每个节点通常都是可修复或可替换的。因此，对于这类集群数量动态变化且可修复的分布式系统而言，传统的框图分析法和故障树分析法等静态方法已经不再适用。

在可修复系统的相关研究中，由于马尔可夫模型能够很好地对这类状态经常变化的系统进行可靠性分析而被广泛地应用[7-10]。对于某些特定系统，由于其某些状态无法被确定，因此对此类系统的研究使用隐马尔可夫模型[11-12]。此外，对于某些特定系统而言，其运行期间的状态是历史相关的，针对此类系统，文献[13]给出了分析方法，文献[14-16]在其基础上做了进一步的研究。

对于分布式系统的可靠性研究，主要分为以用户为中心的方法、基于架构的方法和基于状态的方法[4]。在基于状态的方法中，文献[17]将各种错误分为不同的层次，并将这些层映射到不同的马尔可夫状态，通过排队论、图论和贝叶斯分析来预测系统的可靠性。文献[18]基于传输时间模型，评估程序在分布式系统中的执行时间，并结合时间约束信息定义相应的马尔可夫状态从而计算可靠性。文献[19]统筹考虑资源、元素、工作时间、节点和链路等因素来搜索最小资源生成树，并使用条件概率来计算系统的可靠性。

基于云的分布式应用程序的可靠性分析/建模和性能指标具有挑战性[4]，因为云系统中任何资源的故障都可能使在该环境下运行的整个应用程序崩溃。文献[20]对硬件故障特征进行了详细的分析并初步地分析了硬件故障预测指标。文献[21]提出了信任评估模型，可有效地重新配置各种云资源并将其分配给多个用户请求。文献[22]将错误归纳成8类，进而划归到服务请求和服务执行2个阶段，对这2个阶段进行建模以预测基于云的系统的可靠性。

2 基于马尔可夫模型的可修分布式系统可靠性分析方法

2.1 方法概述

本文提出的分析方法分为3个部分：

1)失效过程：通过对集群中节点的运行指标进行采样，分析这些指标，计算出集群的节点平均失效率，并通过节点平均失效率计算集群的失效概率序列。

2)修复过程：通过对特定集群中节点的修复时间进行统计分析，找出其修复时间服从的概率分布，并根据该分布得到集群的修复概率序列。

3)稳态分析：从失效概率序列和修复概率序列计算集群的Markov状态转移矩阵以及矩阵对应的单位稳态向量，结合特定分布式系统的特性对该稳态向量作进一步的分析。

2.2 状态空间的定义

对于一个具有n个节点的分布式系统，定义其状态空间S={0,1,2,…,n}，其中n为集群中的节点数量。对于任意时刻t，集群在该时刻的状态s(t)∈S表示在该时刻集群中正常工作的节点数量。

2.3 失效过程

对分布式集群中节点失效过程的分析基于以下假设：

1)集群通常能容忍部分硬件失效，在短期内其提供服务的可用性主要与其相关性能指标有关。

2)集群中每个节点的相关性能指标都差不多，即集群能保证负载的均衡性。

3)短期内节点间的失效是独立的。

对于单个节点，其可靠性相关指标可以分为2类：突变型与渐变型。

突变型指标值的变动通常不会对节点可靠性造成影响，然而一旦该指标值超过某个阈值，节点立即处于不可用状态，例如节点的套接字个数与文件描述符，在Linux系统中通常它们的最大值为65535，一旦达到该值，则节点无法接受新的TCP连接以及打开新的文件，在这种情况下直接将该节点标记为不可用。

渐变型指标通常是与节点负载相关的指标，例如CPU、内存、磁盘或网卡的利用率。随着指标值的增加，节点的可用资源会逐步减少，在请求节点资源时通常会导致较高的延迟甚至资源请求失败。因此，定义渐变型指标的失效概率函数如下：

(1)

其中，x为当前时刻测量指标所占其阈值的比例，x∈[0,1]。Δx为指标当前时刻与上一时刻测量值的差值，Δx∈[-1,1]。a是一个常数，表示失效概率对负载的敏感程度，a越大越敏感，a∈(0,∞)。该函数的值表明在下一个采样周期内节点可能失效的概率。当然，也可以针对不同分布式系统本身的特性来定义不同的失效概率函数，或者基于系统的历史统计数据给出其在给定指标值下的瞬时失效率。

在相关研究中，通常认为节点正常工作的时长服从指数分布[23-24]。在本文中，由于一个采样周期通常较短，因而可以认为在该采样周期内的节点失效率是恒定的，即节点的失效概率满足无后效性，服从指数分布。则由指数分布的概率密度函数可知：

(2)

其中，λe表示节点的瞬时失效率，T表示采样周期的时长，由此可计算得出节点在该采样周期内的瞬时失效率为：

(3)

在节点数n较大而节点平均失效率较小的情况下，节点失效的过程为一个泊松过程是一种合理的假设[25]，则单位时间内失效的节点个数λ=n(1-e-λe)。若s(0)=m,m≤n,对于给定的时间t，集群截止到t时刻失效k个节点的概率为：

(4)

由于该状态下的集群不可能失效超过m个节点，超过的情况等价于失效m个节点。因此，对于节点数为n的分布式集群，在s(0)=m的情况下可得在给定时间t内的失效概率序列fm(k)，如表1所示。

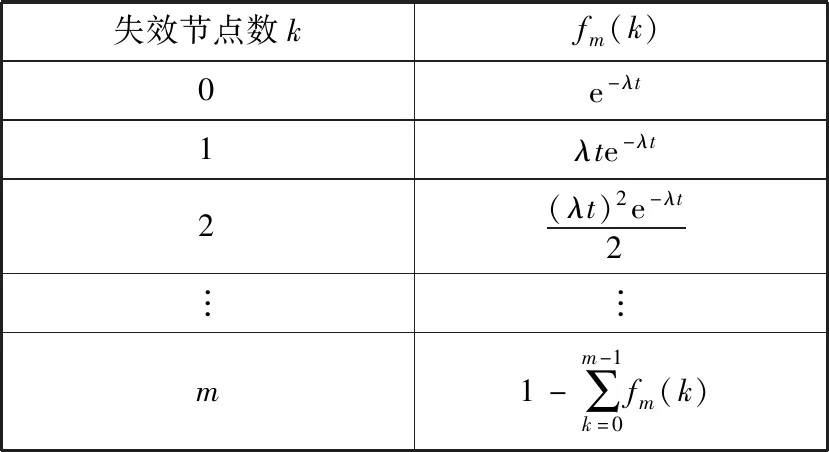
表1 失效概率序列

为了计算上的方便，对于表中未列出的情况，定义其失效概率为0。

2.4 修复过程

针对节点失效后的修复，一般情况下可以认为是对组成该节点的各个成分进行重新部署，例如：更换硬件服务器、重新安装操作系统、重新安装软件、配置应用软件等。

如果将上述每个过程中所耗费的时间用随机变量Z1，Z2，…，Zn表示，则根据李雅普诺夫中心极限定理，修复单个节点耗费的总时间Y=Z1+Z2+…+Zn在修复流程较多时是趋近于正态分布的。

若维修第k个节点所需要的时间为随机变量Xk,Xk～N(μ,σ2)，其中μ和σ分别为实验测量所得到的修复时间的均值和标准差。

由于维修每台服务器的过程是一致的，则在节点硬件条件一样的情况下，每台服务器的修复时间是独立同分布的。因而由中心极限定理可知：

(5)

因此，对于节点数为n的分布式集群，在s(0)=m,m≤n的情况下可得在给定时间t内的修复概率序列rm(k)，其对应的事件如表2所示。

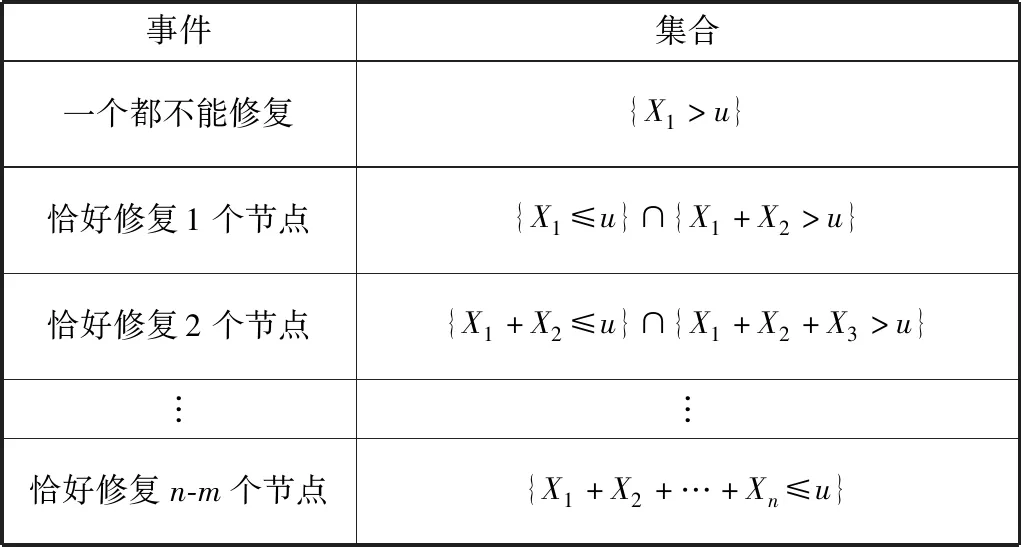
表2 维修事件

修复概率序列rm(k)对应的概率如表3所示。

表3 修复概率序列

为了计算上的方便，对于表中未列出的情况，定义其修复概率为0。

2.5 可靠性分析

对于s(0)=m,m≤n，可以得到2个序列fm(k)与rm(k)。由此，可以得到一个以s(0)=m为初始条件的到t时刻的状态转移序列wm(τ),-m≤τ≤n-m:

(6)

其中，rm(k)与fm(k)可从表1与表3得到。针对每一个不同的初始状态，可以构造整个分布式集群的Markov状态转移矩阵为：

(7)

其中，Mij=wi(j)表示从集群当前状态s(0)=i一步转移到状态s(t)=j的概率。

下面给出一个4节点的分布式系统状态转移矩阵的求法示例。通过对该系统的指标进行采样，若当前存活节点数为2，则由失效过程和修复过程的分析可得其失效概率序列f2(k)与修复概率序列r2(k)，假设它们的取值为表4中的值。

表4 示例概率序列

由式(6)可得系统从当前状态s(0)=2的状态转移序列：

(8)

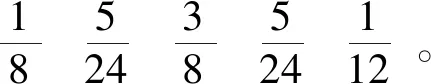
在集群的失效和修复过程中，其中间的每个状态都是可达的，即该Markov矩阵是不可约的，因此该矩阵必定存在一个特征值为1的特征向量。求该特征向量，并将其单位化，即可得系统可能长期处于各个状态的稳态概率向量，用veig表示。

对于分布式系统来说，仅能容忍部分节点失效。针对不同分布式系统本身的特性，可以选取一个加权向量vw，则该分布式系统的可靠性可定义为：

r=vwT·veig

(9)

3 实验与结果分析

3.1 实验拓扑

实验对一个Ceph分布式存储系统做了可靠性分析，实验拓扑如图1所示。

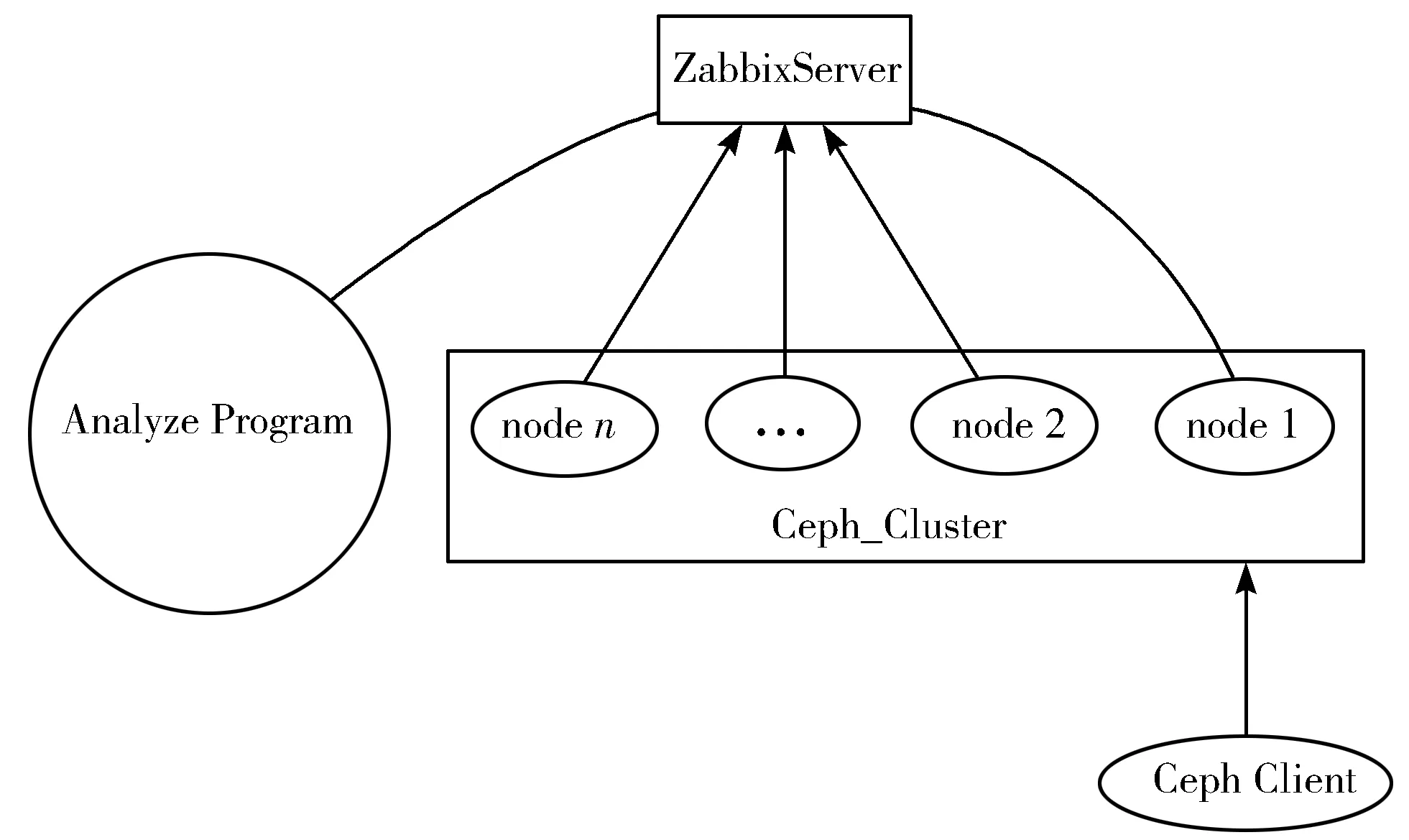
图1 实验拓扑

通过Zabbix对该集群的软硬件情况加以监控，分析程序通过Zabbix API获取这些数据并计算出该系统的可靠性指标。真实情况下的存储服务可用性则由Ceph Client的I/O失效率给出。

3.2 节点修复时间的正态性检验

针对Ceph集群中存储节点的修复时间，实验采集了40个节点的修复时间，它们的高斯核密度估计函数如图2所示。

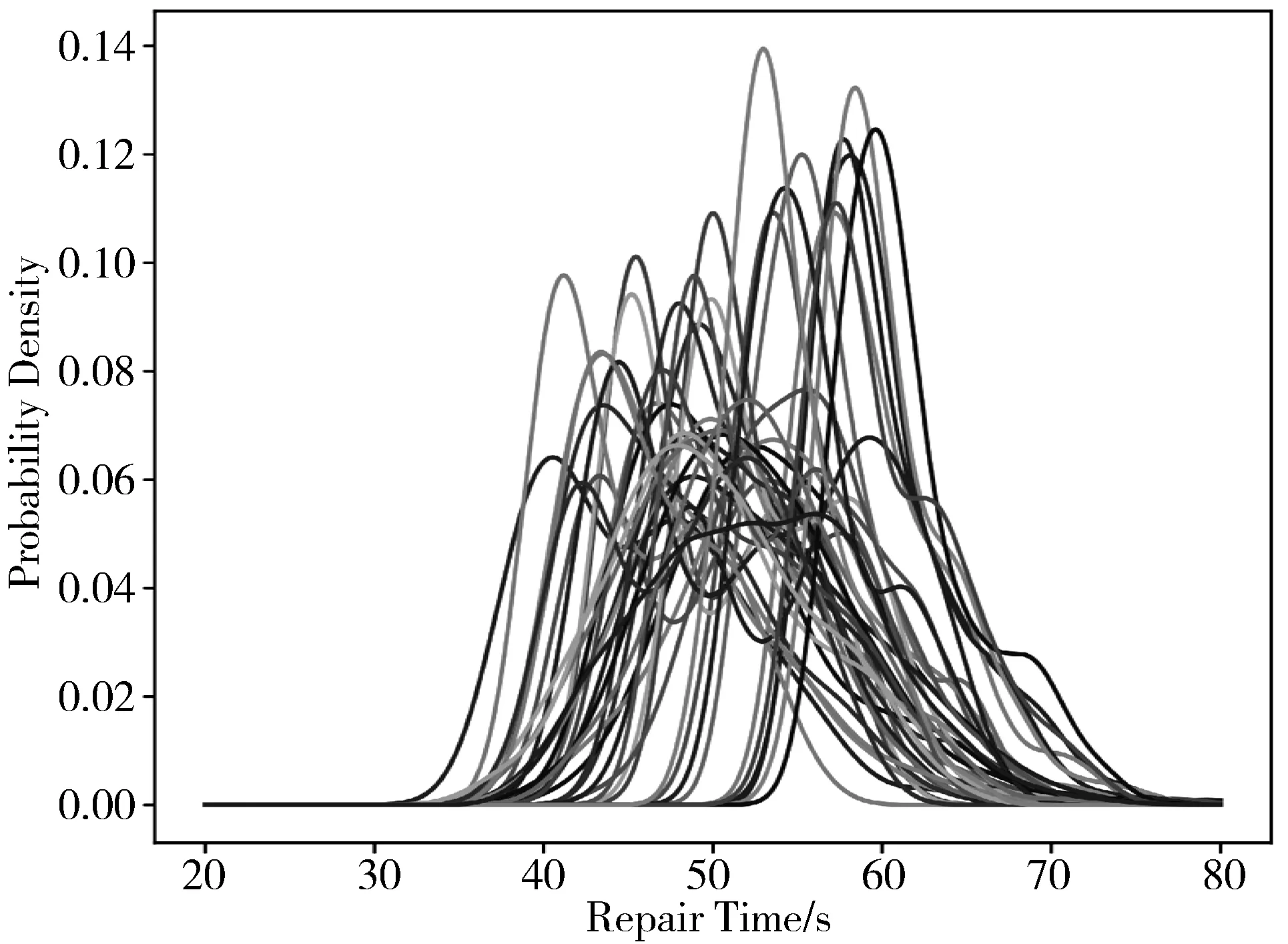
图2 节点修复时间核密度估计

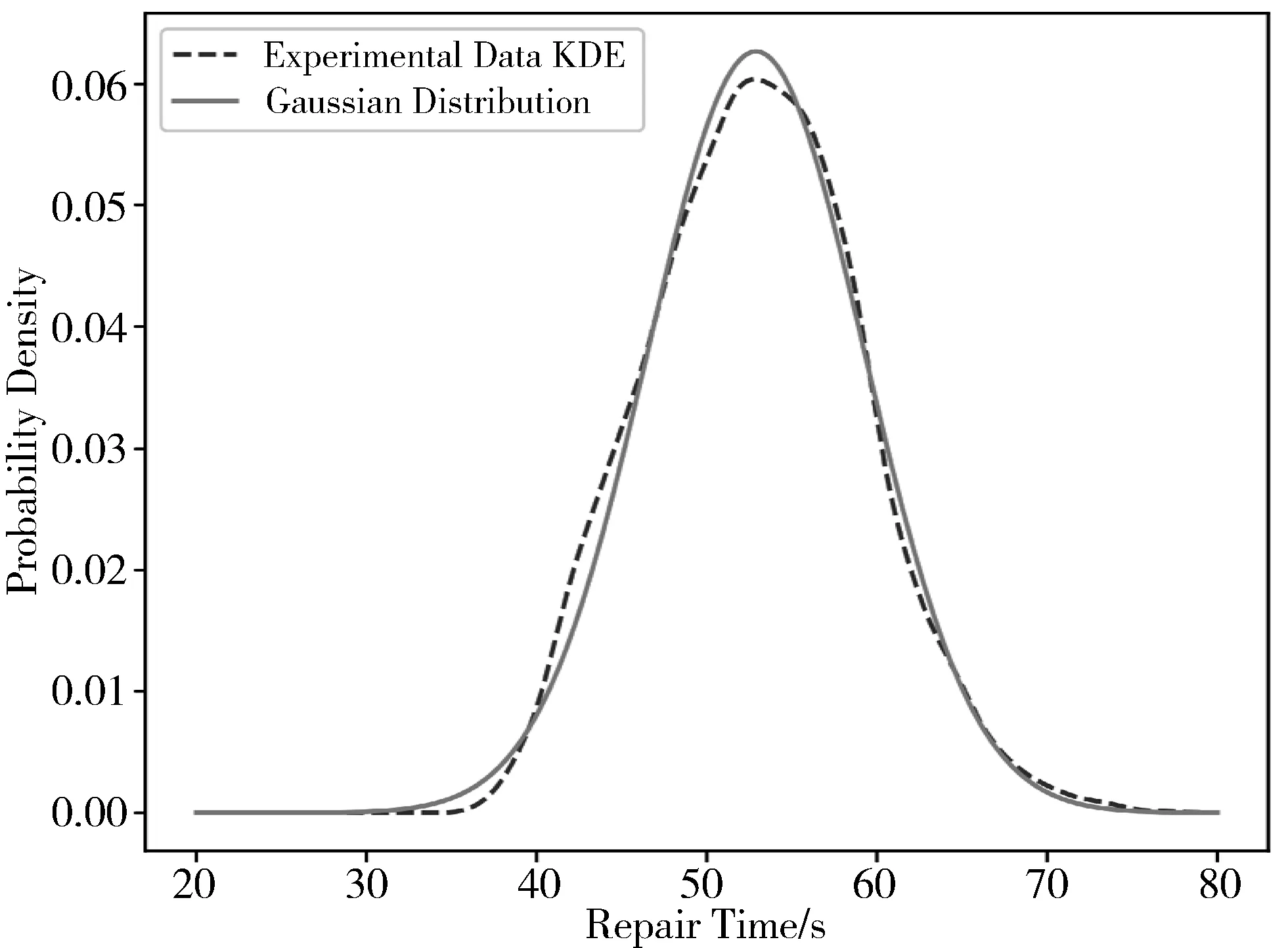
图3 总体修复时间核密度估计

使用Kolmogorov-Smirnov检验方法对实验数据的分布进行正态性检验，得到D=0.0135,P=0.0755，因此可以认为节点的修复时间服从正态分布，从实验上验证了2.4节中的假设。

3.3 用户请求质量与系统可靠性对比

由于Ceph本身特性[26]，其OSD存储进程会缓存用户的读取数据，为了更加真实地测量其I/O性能，选取写操作作为用户的请求方式，块大小设为大部分操作系统默认的4 kB。随着对Ceph集群负载的逐步提升，其用户的4 kB写延迟与单个服务节点的平均写带宽如图4所示。

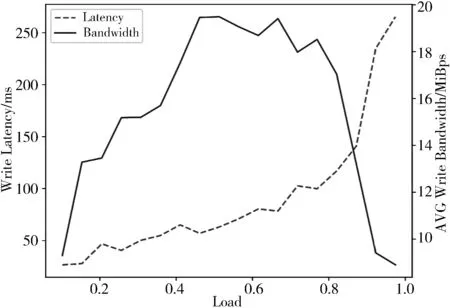
图4 用户写延迟-节点平均写带宽

从图4可以看出，随着用户写请求的负载升高，单个服务节点向外提供的写入速率逐渐上升，并于50%负载左右达到其服务能力的最大值，并在该负载区间附近能稳定地向外提供服务。在此区间内，由于需要为越来越多的用户提供服务，用户的写请求需排队等待服务，用户的写入延迟近似地呈线性增加。随着用户请求负载越来越高，单个节点的服务能力会随着网络、磁盘等硬件资源的耗尽而逐步下降，写延迟继续上升。当负载超过80%后，系统会由于用户的大量请求而产生资源争用的情况，在这种情况下，单个节点向外提供的写能力急剧下降，且由于请求用户众多，平均分配给每个用户的可用写带宽就不足以满足用户的需求，同时此阶段内用户的写延迟急剧上升，也不足以满足用户对正常写操作的延迟要求。

为了分析用户I/O请求的质量，通过在多个客户节点上运行I/O进程，测试它们在不同集群负载情况下I/O的延迟和可用带宽的质量等级占比。大量重复实验表明：在集群正常负载的所有的测试结果中，延迟小于200 ms的请求占总请求数量的81%，延迟大于200 ms同时小于400 ms的请求占总请求数量的14.1%，因此以200 ms和400 ms为界限将用户的请求分类为“良好”“可用”和“失效”3个部分，其中可用的部分包含良好。同理，根据用户可用带宽将其请求也分为这3个部分，它们在不同负载情况下占总请求数量的比例如表5所示。

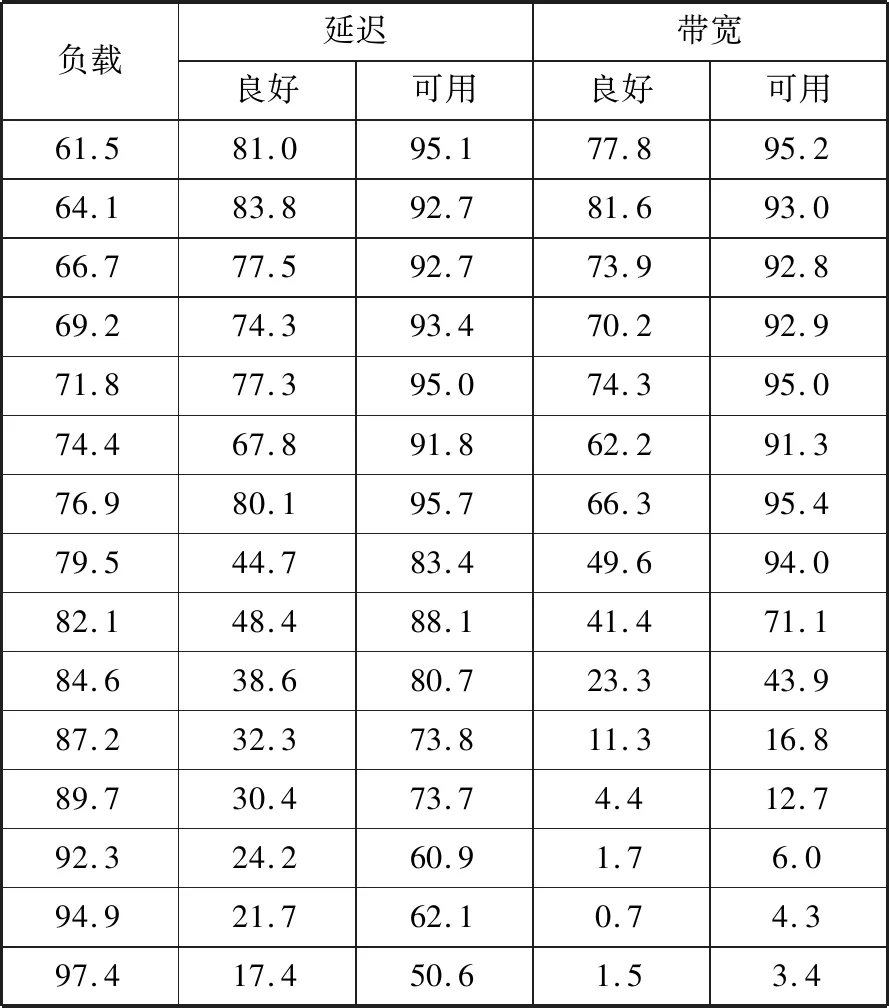
表5 延迟-带宽质量等级占比 单位：%

综合考虑延迟与带宽在不同等级中的比例，并以较低的值为准，它们与本文方法计算所得的可靠性的对比如图5所示。其中本文方法计算可靠性的步骤如下：

1)将3.2节中得到的样本均值和样本标准差代入表3可得系统的修复概率序列。

2)式(1)中取a=5，结合系统运行期间Zabbix采集到的数据，根据表1可得系统的失效概率序列。

3)将步骤1与步骤2中的结果代入式(6)，可得系统的马尔可夫状态转移矩阵，并可计算出对应的稳态向量veig。

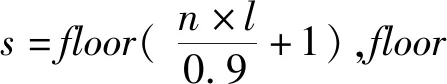
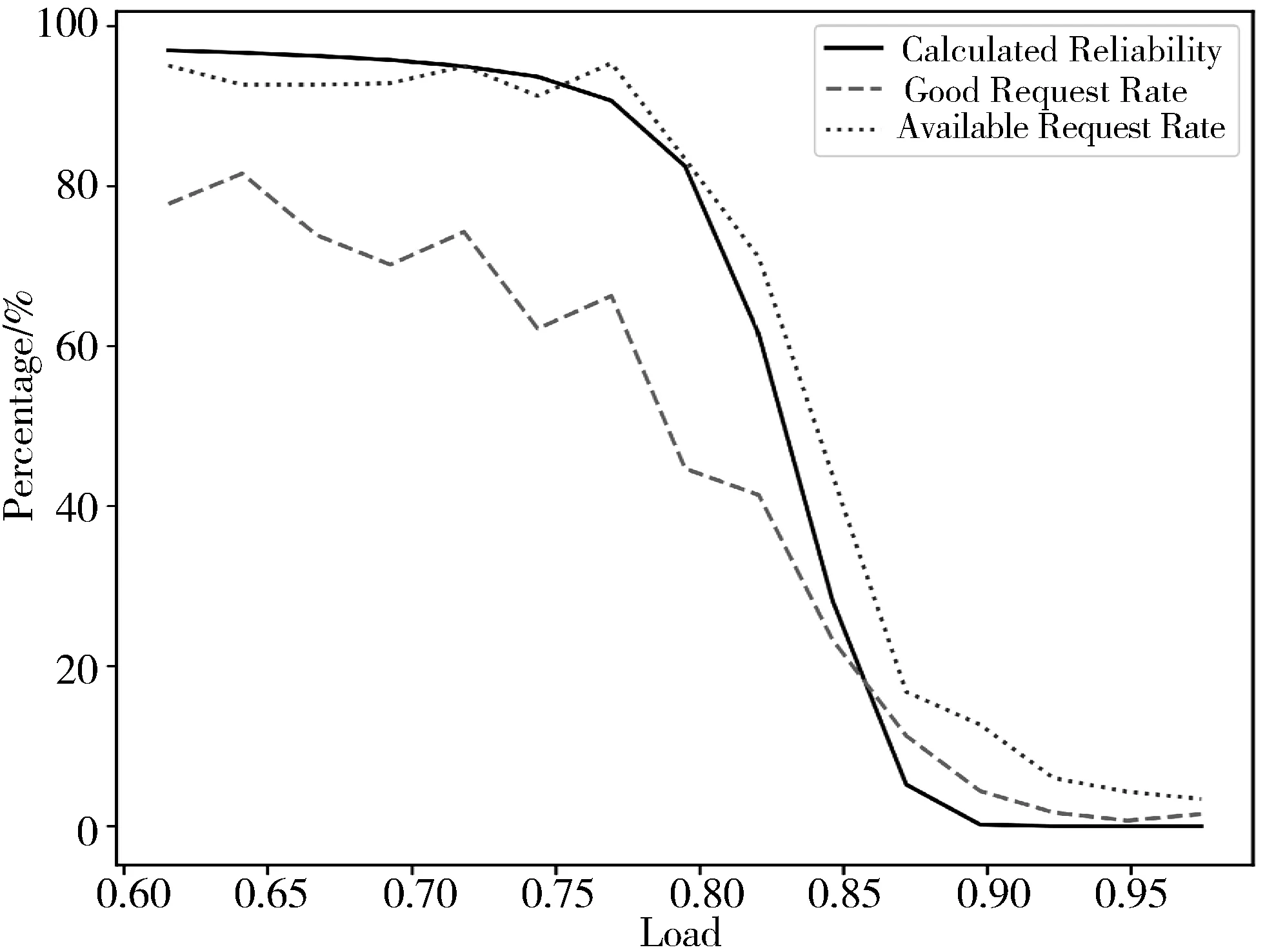
图5 I/O质量等级占比与可靠性的对比

从图5中可以看出，本文方法计算所得的可靠性指标的理论值大部分都位于请求质量等级“良好”与“可用”附近和它们之间的区域内。而对于极高负载区间内理论值小于实验测量值的情况，这主要是因为Ceph节点处磁盘调度算法导致的，为了最大化磁盘的吞吐量和降低平均寻道时间，通常驱动程序会将多个I/O请求统筹考虑，选择开销最小的读写方式，而这可能会导致用户后提交的I/O请求反而先被响应。因而在所有的用户请求中，始终会有极小的一部分I/O请求被很快地响应，这也就解释了在极高负载区域内仍然存在一小部分“良好”与“可用”等级的I/O请求这一现象。然而对于单个用户而言，其多个请求都被快速响应的可能性极小，因此，在集群负载极高时从单个用户的角度来看系统是不可用的。由此可见本文方法计算所得出的可靠性指标能较好地反映系统的真实情况。

与传统的方法相比，本文方法通过对系统的失效过程与修复过程进行分析，简化了系统的状态空间，解决了传统方法在系统规模较大时因状态空间爆炸而导致的求解困难问题，扩展了传统马尔可夫模型方法的适用条件，使其可用于规模较大的分布式系统。此外，传统方法通常假定节点的失效概率服从某一特定分布，未考虑系统在运行期间的具体状态，本文方法在系统运行期间动态获取其软硬件状态，并及时地更新系统的状态转移矩阵和可靠性指标，相对于传统方法能更加准确地反映系统的真实情况。

4 结束语

本文基于马尔可夫模型，针对云计算环境下的可修分布式系统，研究了它的失效过程和修复过程，并通过这2个过程得到的失效概率序列与修复概率序列计算系统的马尔可夫状态转移矩阵以及稳态向量，然后通过这个稳态向量对系统的可靠性做分析。最后对一个分布式存储系统进行了可靠性建模，用实验验证了本文方法的可用性和有效性。

在未来的工作中，笔者将针对云计算环境中含有大量异构设备的分布式系统进行研究，使得本文的方法能够更加准确地反映这类系统的实际部署情况。