基于自步数据重构正则化的模糊C均值聚类算法改进

陈怡君，曹逻炜，杜玉倩

(1.西安航空学院，陕西 西安 710077； 2.中国特种设备检测研究院，北京 100029；3.西安交通大学数学与统计学院，陕西 西安 710049)

0 引 言

聚类分析是模式识别和知识发现中一个极为重要的技术，其目标是将一组具有未知分布的数据划分聚集，从而使得具有相同性质的数据归并为同一类或簇，具有不同性质的数据点划分为不同的类或簇[1-2]。因其可从观测数据集中发现不同的结构信息，自20世纪60年代以来一直受到各个领域专家的普遍重视，并被广泛应用于工程、生物、心理、计算机视觉、图像处理等领域[3-7]。在众多聚类算法中，C均值算法因其简单、易于理解且能对大型数据集进行高效分类，常常被用于聚类任务[8]。在C均值算法中，每个数据点只能属于一个类，并通过“类内距离平方和最小化”准则来实现对数据点的划分。C均值算法对数据的归属是一种硬性的划分。然而，现实中对数据的归属并不是界限分明的，因此模糊划分的概念被引入到聚类分析当中。为了实现模糊聚类，Bezdek[9]将C均值算法进行推广，提出了模糊C均值算法。模糊C均值算法假定隶属度(即：反映数据点隶属于某个类的程度)不仅可以取值0或者1，而是可以取到0～1之间的任何数，并且通过“类内加权距离平方和最小化”准则来实现对隶属度的模糊化。另一种对隶属度的模糊化方式就是对C均值算法的目标函数进行正则化加权，Miyamoto等人[10]提出了一种熵正则化模糊C均值算法，Miyamoto等人[11]进一步提出了一种二次项正则化模糊C均值算法。这些方法在改善模糊C均值算法性能方面有了较大提升[12-15]，但仍存在对初值敏感、易陷入局部收敛等问题。

本文提出一种自步数据重构正则化模糊C均值算法(Self-paced Data reconstruction Regularized Fuzzy C-Means, SDRFCM)。假定类中心不仅能反映每簇数据的共性特征，而且能够近似线性重构部分数据点，本文提出的SDRFCM将数据重构约束作为正则化来实现对隶属度的模糊化。此外，鉴于部分数据具有噪声或无法线性重构，在SDRFCM中以自步学习的方式来逐步实现数据点的模糊聚类。在模拟数据、实际数据、图像分割上的实验进一步验证了本文算法的有效性。

1 模糊C均值及其模糊正则化

1.1 C均值和模糊C均值

设数据集D中含有m维空间的n个数据点，分别记为：

xi=(xi1,xi2,…,xim)T,i=1,…,n

(1)

C均值(C-Means, CM)聚类的目标是寻找c个聚类中心：

vj=(vj1,vj2,…,vjm)T,j=1,…,c

(2)

并估计每个数据点xi隶属于哪个类。记uij为第i个数据点xi隶属于第j个类的指示函数(或称为隶属度函数)，则C均值算法通过最小化类内距离平方和：

(3)

来估计聚类中心vj和隶属度uij，其中：

(4)

且满足约束：

(5)

C均值通过交替更新隶属度uij和聚类中心vj来使得评价函数Jcm最小。

C均值聚类是一种对数据的硬聚类，它要求隶属度uij取值为0或1。然而，在现实世界中，数据样本的类属不是界限明确的，具有某种不确定性。因此，在模糊C均值(Fuzzy C-Means， FCM)算法中，隶属度uij可以是[0,1]区间中的任何一个值，其大小表示数据点xi隶属于第j类的程度。这种取值空间的变化可视为对隶属度的模糊化。FCM通过在标准C均值算法的目标函数中引入对隶属度uij的指数加权来实现，即最小化加权类内距离平方和：

(6)

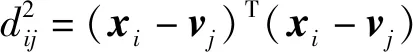
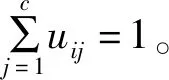
步骤2根据下述公式更新聚类中心vj：

步骤3根据下述公式更新隶属度uij：

i=1,2,…,n;j=1,2,…,c

步骤4停机检验：如果目标函数不再发生变化或变化较小，或者达到预先设定的最大迭代，则算法停机并输出隶属度uij和聚类中心vj；否则，转步骤2。

1.2 隶属度的模糊正则化

标准的模糊C均值算法通过对硬分类C均值目标函数中的隶属度uij进行指数加权对其进行模糊化。另一种对隶属度uij模糊化的方式是对C均值的目标函数Jcm进行正则化。例如：文献[6]提出了熵正则化模糊C均值算法，其目标函数为：

(7)

其中，λ为正则化参数，用于调节隶属度uij的模糊程度。熵正则化模糊C均值算法和标准模糊C均值算法流程一样，所不同的是对隶属度uij的更新变为：

(8)

与标准模糊C均值算法的指数加权作用相似，熵正则化项的引入使得隶属度uij由原来的硬性分类变为模糊化分类。

同样从信息论的角度出发，Ichihashi等人[16]利用隶属度的K-L信息来取代熵对其进行正则化，提出了K-L信息正则化模糊C均值算法，其目标函数如下：

(9)

其中，πj为第j类的先验概率，∑j为第j类的方差。

文献[10]利用隶属度uij的二次函数对C均值算法进行加权，得到如下目标函数：

(10)

研究文献[13-17]发现，通过在标准C均值算法中添加正则化项，可以对隶属度进行模糊化，从而提升聚类算法的性能，改善聚类的效果。

2 自步数据重构约束模糊C均值聚类

2.1 数据重构

对数据进行聚类，除了能够得到每个数据点的隶属度uij以外，还可以得到每类的类中心向量vj。一般来讲，类中心向量vj对聚类结果影响严重，好的聚类中心应能够尽量代表数据点。从数据表示的观点出发，类中心向量vj应具有代表性，其所构成的空间可以表示大部分数据点且表示系数和每个数据点的隶属度uij相关。因此，假定数据点xi可以由类中心向量vj和它的隶属度uij表示，并能够通过极小化以下重构误差平方和来得到类中心和隶属度，即：

(11)

其中，fi为xi的重构函数。考虑到问题的可解性，假设重构函数fi是线性的，即：数据点xi可由类中心向量v1,…,vc近似线性表示：

(12)

其中，V=[v1,…,vc]为类中心向量组成的矩阵。将上述近似线性表示关系式代入式(11)，重构误差平方和变为：

(13)

2.2 自步学习

上述重构误差平方和R假定类中心向量v1,…,vc不仅能反映每簇数据的共性特征，而且能够线性表示数据点。但是，并不是所有的数据点xi都可以由类中心向量v1,…,vc线性表示的，例如：噪声数据点、异常值以及部分数据点是无法用类中心向量v1,…,vc线性表示的。为此，本文引入了对数据点xi的自适应选择策略——自步学习(Self-paced Learning)。

受人类学习过程的启发，Bengio等人[18]提出了课程学习(Curriculum Learning)的概念，并认为模型的学习应该是一个样本从“易”到“难”逐步引入的训练过程。此处的“易”是指样本的质量较好，“难”是指那些数据质量相对较差的数据点，比如含噪声的或异常的数据点等。然而，要区分数据的难易并不是一件简单的事情。为此，Kumar等人[19]把课程学习理论归结为一个简洁的优化模型，并将这一模型称之为自步学习。

自步学习模型包含2项：损失项和对权重的正则化项。损失项是对所有样本的加权损失度量，正则化项是对样本损失权重的先验正则。自步学习逐步调节自步参数来自适应地选取质量较好的样本，对模型的训练可通过最小化以下目标函数来实现[20-21]：

(14)

其中，li为样本xi的损失度量函数；w为模型参数；si为指示样本xi难易程度的权重，且si取值为0或1；τ称为年龄参数，用于控制学习的节奏；f(s;τ)称为自步学习正则化项，它可以取不同的形式，一般可令：

(15)

2.3 自步数据重构正则化模糊C均值

依据上述分析，假定类中心向量v1,…,vc能够近似线性重构部分数据点xi，且可以通过自步学习的方式逐步对这些数据点进行筛选，本文提出一种新的模糊C均值聚类算法，称之为自步数据重构正则化模糊C均值(Self-paced Data reconstruction Regularized Fuzzy C-Means, SDRFCM)。其目标函数定义为：

(16)

其中，α为数据重构误差项的正则化参数，用于调节可重构的数据点的多少。此外，隶属度uij和si还应满足以下约束:

(17)

在满足上述约束的条件下，对SDRFCM的目标函数进行极小化的问题可以分解为以下n个子问题：

(18)

其中，ui=(ui1,ui2,…,uic)T为数据点xi的隶属度向量。易求得，上述子问题关于优化变量si的最优解为：

(19)

1)当si=0时，上述极小化子问题变为：

(20)

其中，di=(di1,di2,…,dic)T为数据点xi到类中心的距离向量，容易求解其最优解为：

(21)

2)当si=1时，上述极小化子问题变为：

(22)

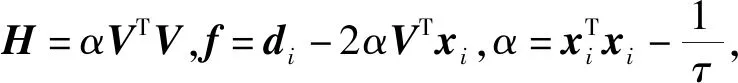
(23)

此二次规划问题可以采用经典的优化方法，如：内点法、有效集法等，对其进行求解。

在隶属度uij和自步学习变量si确定以后，为了得到类中心向量v1,…,vc，需要最小化以下目标函数：

(24)

为方便计算，先引入以下记号：记V=[v1,v2,…,vc]，U=[u1,u2,…,un]，X=[x1,x2,…,xn]，

(25)

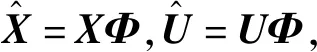
(26)

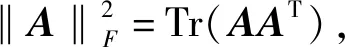
20世纪50年代末，美国语言学家约瑟夫·H·格林伯格打开了语言学研究的一个新的领域——语言类型学。该理论主要的观点是在对人类语言的机制和规则进行概括总结时，必须要进行跨语言验证，而要研究任何一种语言的特点都离不开跨语言比较出的共性和类型分类的基础。我国著名英语学者许国璋也提出：“过去的研究太过于强调汉语和欧洲语言之间的差异，而忽视了两者之间的相同点。”[1]近年来，语言类型学逐渐风靡，挖掘汉语和英语之间的共性和差异，掌握两者之间的普遍特征成为潮流。

(27)

利用公式：

得到函数J关于变量V的偏导数为：

(28)

此外，利用关系式：

(29)

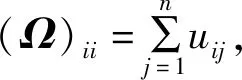
(30)

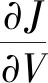
(31)

综上，可以得到有关隶属度矩阵U和类中心矩阵V的迭代更新公式，并利用此公式替换上述模糊C均值算法流程中的有关隶属度和类中心向量的更新部分，则可以得到所提出的自步数据重构正则化模糊C均值算法。

3 数值实验

为了验证算法的有效性，本文分别采用模拟数据、真实的Iris分类数据以及图像数据进行实验，并与标准的模糊C均值算法(FCM)[13]、基于K-L信息的FCM算法(FCMKL)[22]、概率C均值算法(PCM)[23]、模糊概率C均值算法(FPCM)进行比较。此外，本文利用分类精度(Classification Accuracy, CA)来度量算法。为了减少模拟实验随机性对算法性能的影响，各个算法对每一数据集独立运行20次，并分析它们的统计特征值(均值：Average；最好结果：Best；最坏结果：Worst)。

3.1 模拟数据实验

本次实验产生3类数据，每类数据含有100个二维样本点，这3类数据点分别产生于服从不同均值和方差的高斯分布，即：

μ1=(1,2)T,μ2=(-1,-2)T,μ3=(-3,5)T,

(32)

所产生的数据点如图1所示。

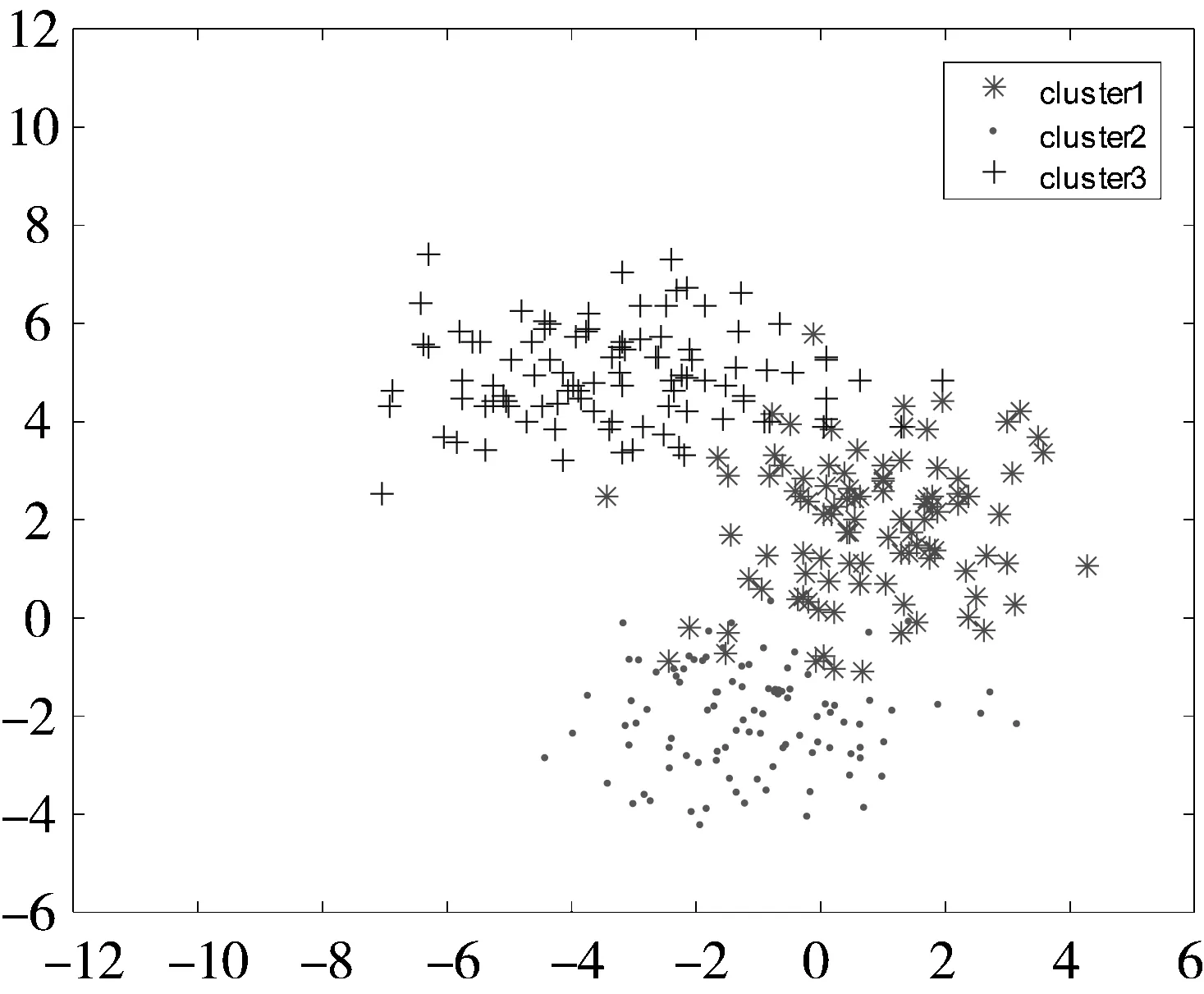
图1 基于不同高斯分布所产生的300个数据点

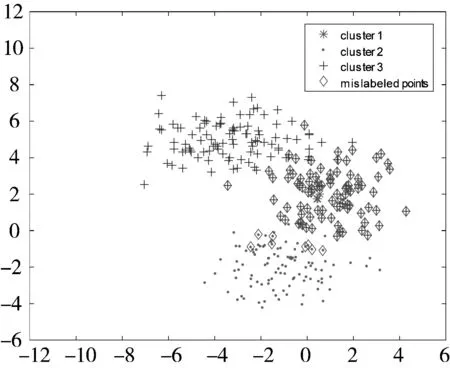
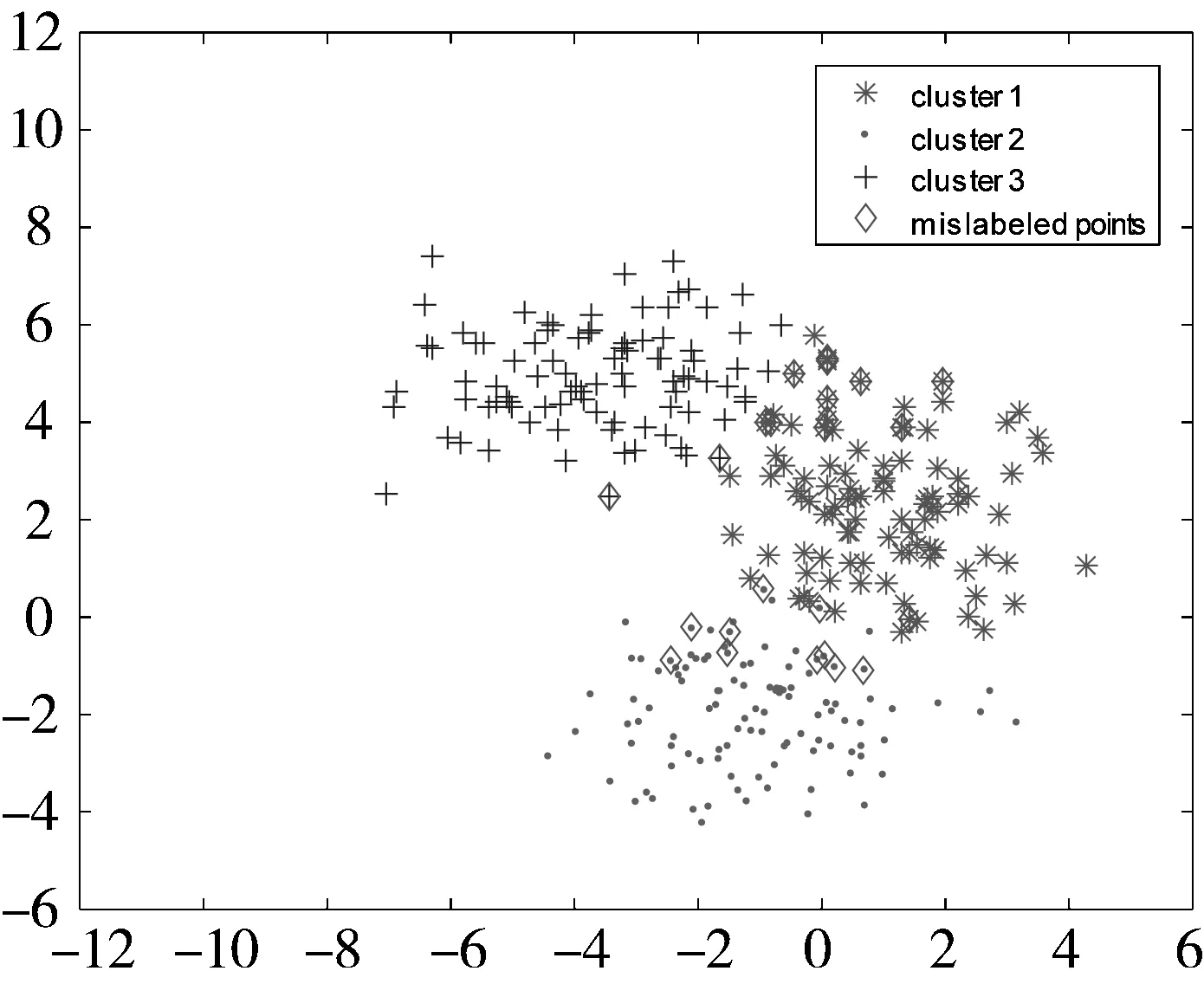
5种聚类算法得到的结果如表1所示。从表1可以发现，虽然几种算法得到的最优聚类精度均为96.67%，但是本文提出的SDRFCM在20次实验中无论平均精度还是最坏精度都优于其他4种算法。图2给出了5种聚类算法在某次实验中的聚类结果可视化比较。

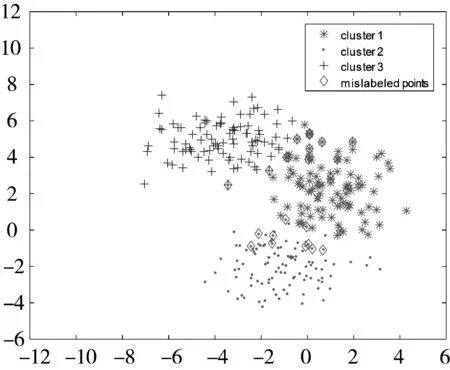
(a) FCM (CA=92.00%)

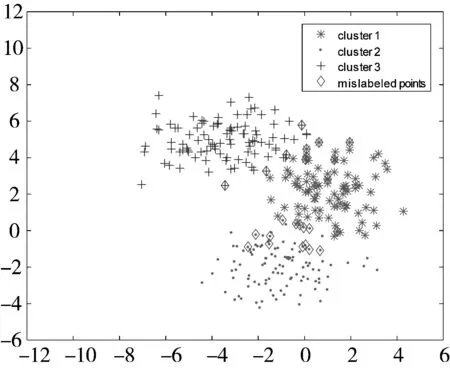
(b) FCMKL (CA=92.00%)

(c) PCM (CA=67.67%)

(d) FPCM (CA=92.00%)

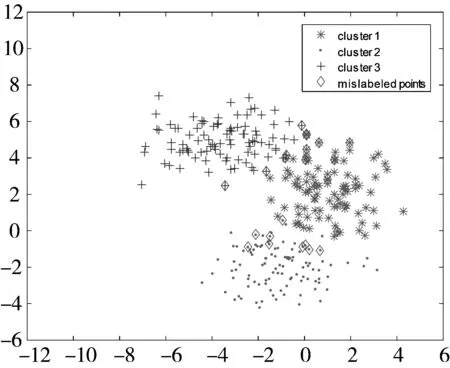
(e) SDRFCM (CA=92.00%)

表1 模拟数据实验中5种聚类算法得到的聚类精度比较

此外，为了进一步比较算法的性能，本文还产生了具有相同方差：

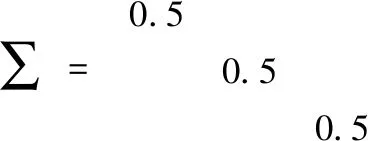
(33)

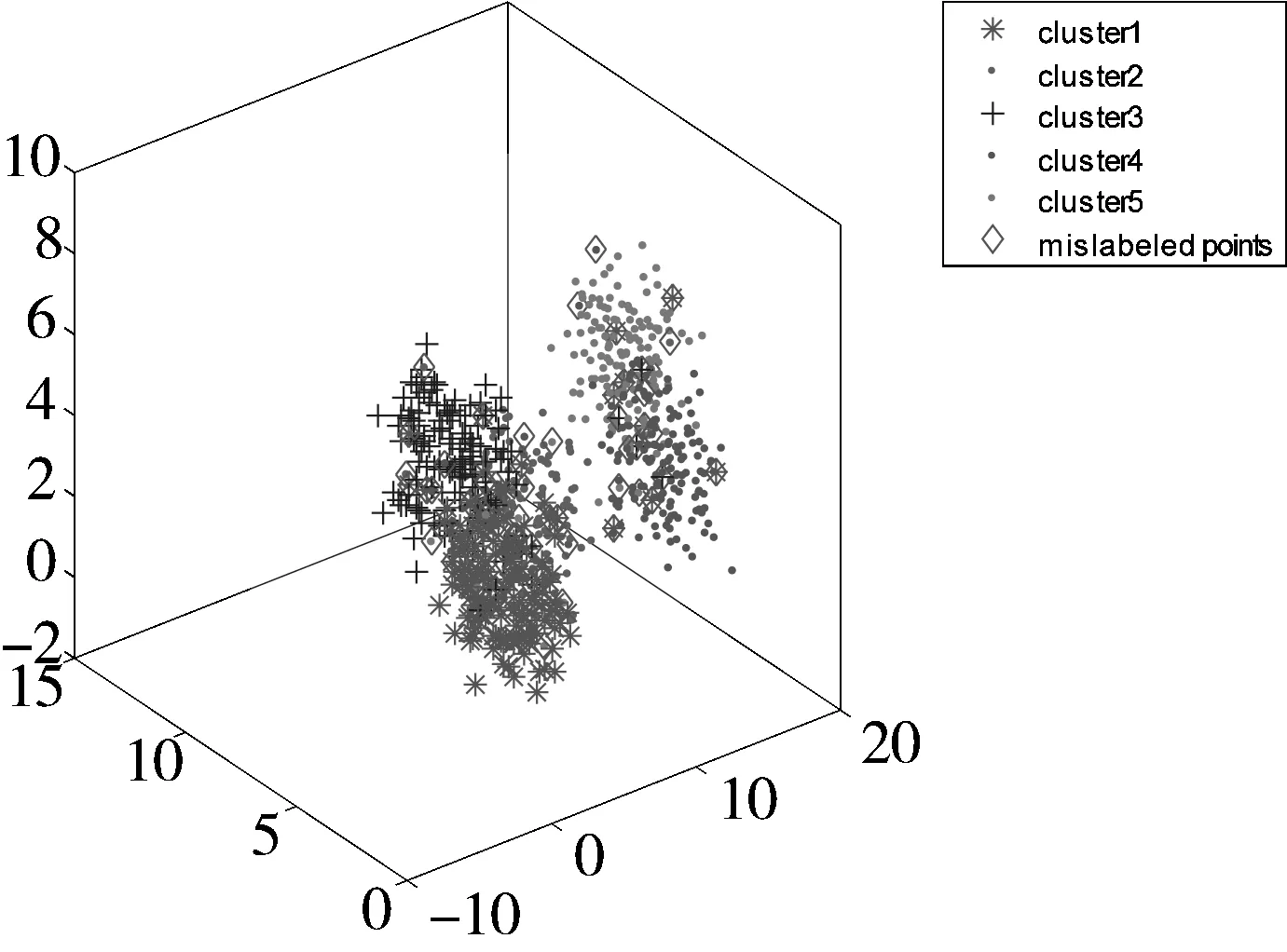
不同均值的、服从高斯分布的5类数据，其中每类包含了150个数据点，共产生了750个数据点，并加入了一定的白噪声，其三维分布如图3所示。与上述实验相似，为了减少随机因素的影响，本文分别进行了20次实验。利用本文提出的SDRFCM以及其他4种算法对其进行聚类，结果如表2所示。从表2可以看出，本文提出的SDRFCM算法略优于PCM算法，但明显较其他3种算法FCM、FCMKL以及FPCM精度更高。图4给出了5种聚类算法在某次实验中的聚类结果可视化比较。

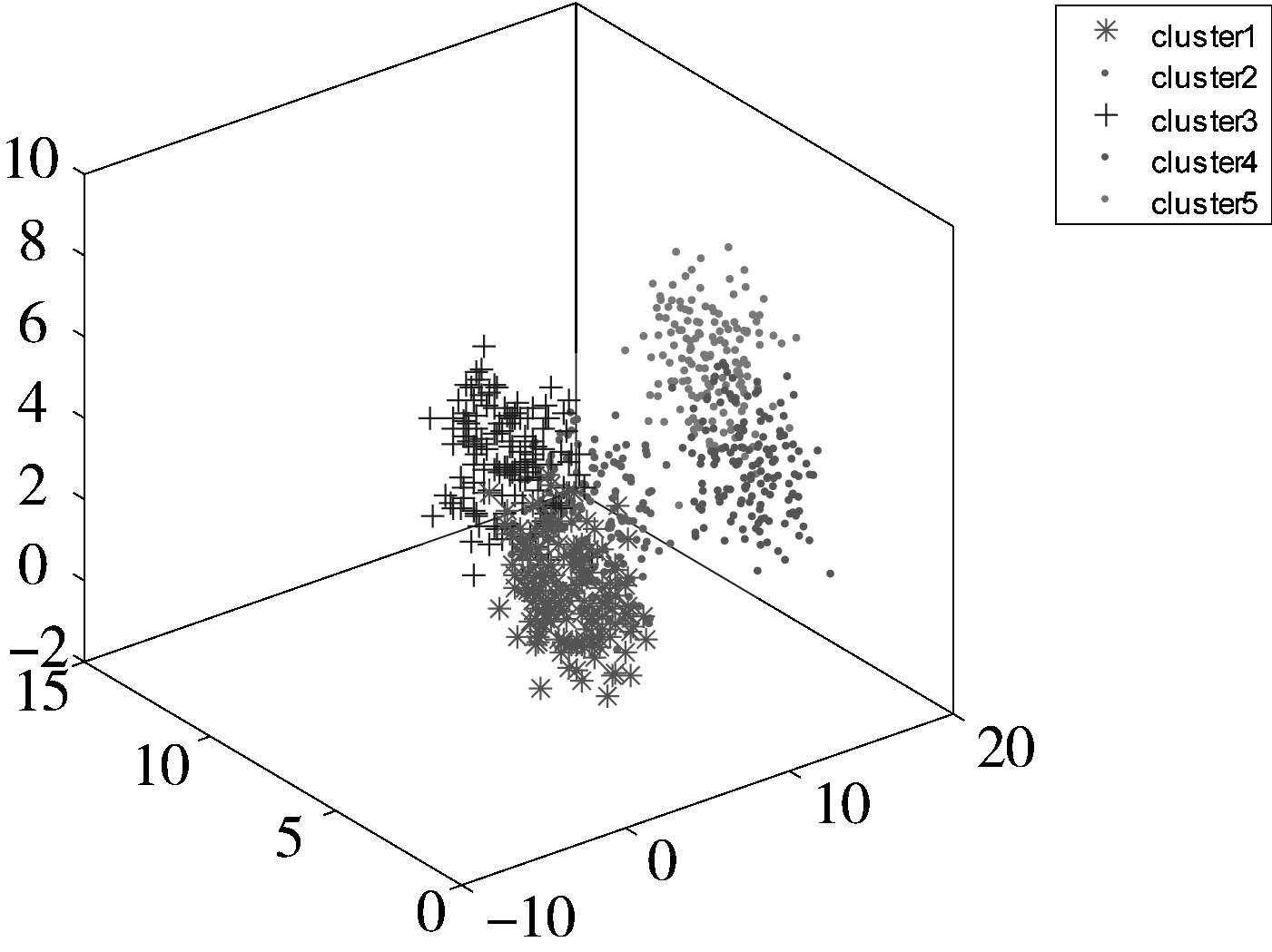
图3 5类模拟数据的空间分布图

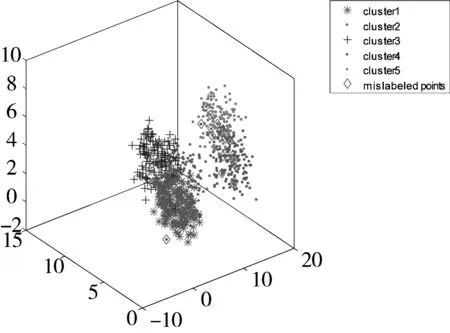
(a) FCM (CA=94.53%)

(b) PCM (CA=92.27%)

(c) FPCM (CA=97.73%)

(d) FCMKL (CA=97.47%)

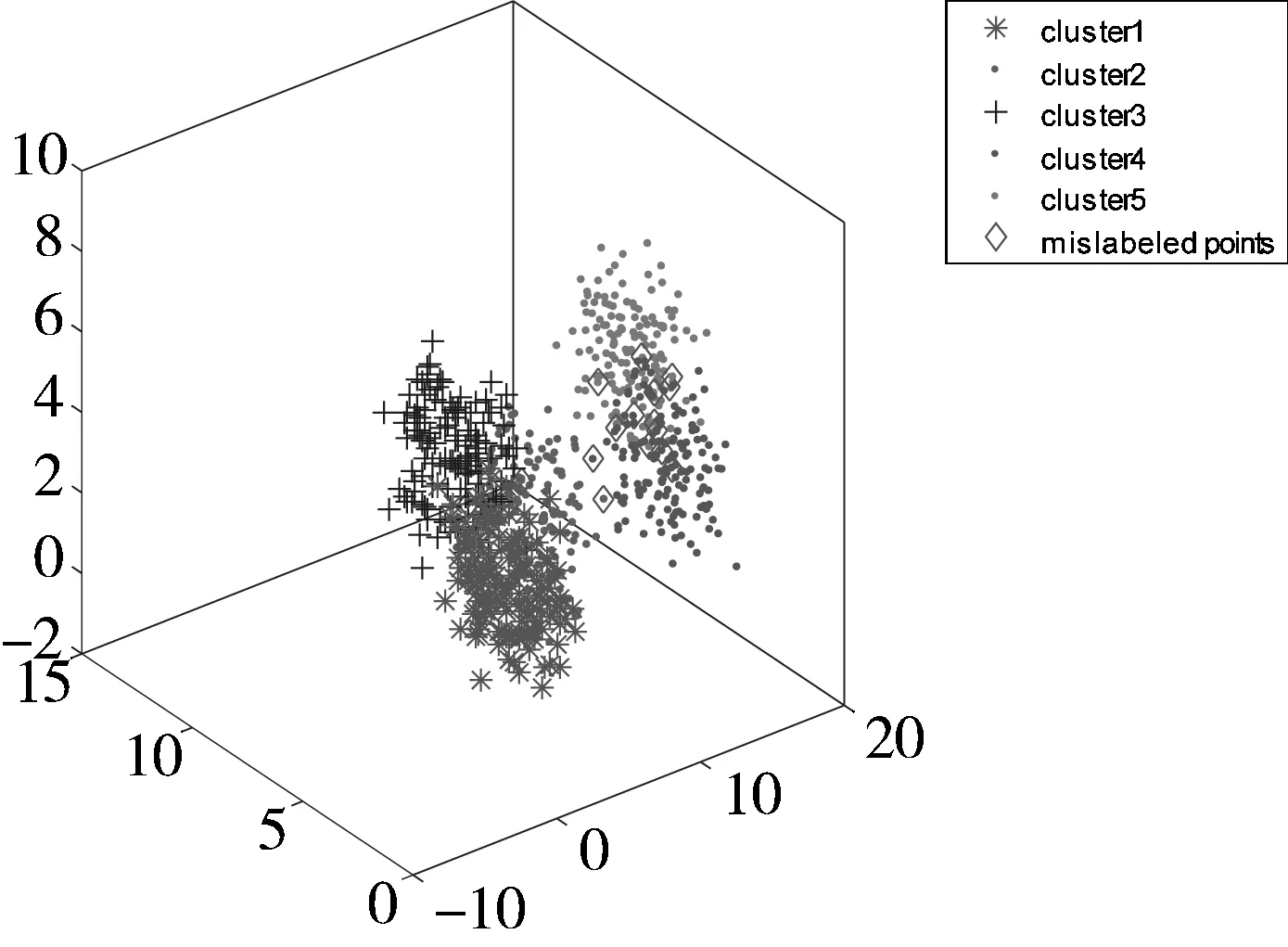
(e) SDRFCM (CA=97.73%)

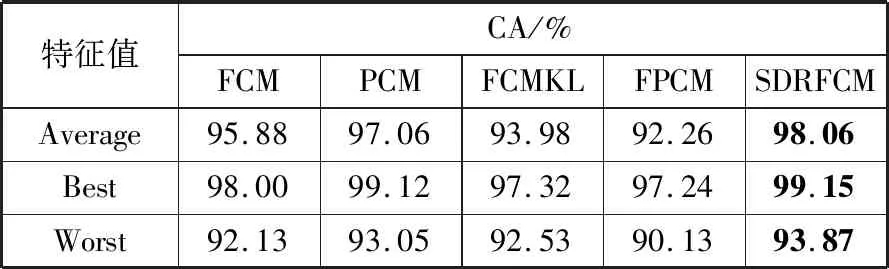
表2 5类模拟数据实验中各个算法得到的聚类精度比较

3.2 Iris数据实验

本次实验采用Iris数据集来进一步测试算法性能。Iris数据集是由著名统计学家Fisher于1936收集整理得到的。它包含了3类鸢尾花卉：Versicolour、Setosa、Virginica，每一类花卉采集有50个样本点，4个属性：花萼长度(Sepal Length)、花萼宽度(Sepal Width)、花瓣长度(Petal Length)、花瓣宽度(Petal Width)。图5给出了3类数据在以花萼长度、花萼宽度、花瓣长度为坐标轴的数据点的分布图。从图5中可以看出，Virginica和Versicolour这2类数据较难完全分开。

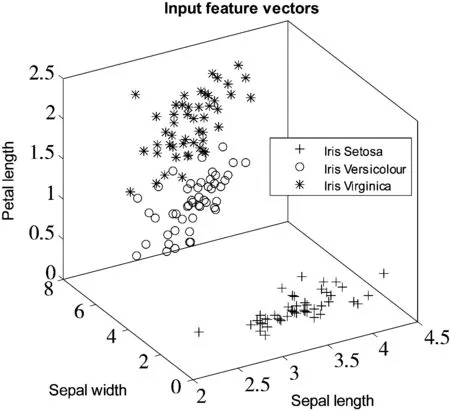
图5 Iris数据点的空间分布图

由于随机初始化聚类中心使得聚类结果不稳定，因此针对此数据集重复进行了20次实验。表3给出了针对Iris数据集的聚类精度对比，其结果进一步验证了本文提出的SDRFCM算法的有效性。

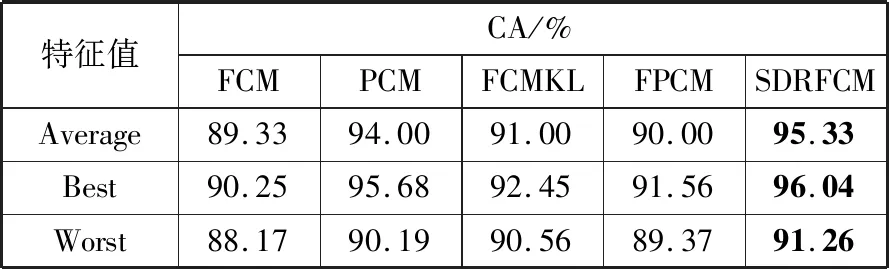
表3 Iris数据集中5种算法的聚类精度比较

3.3 图像分割实验

图像分割是计算机视觉领域一个相对较新的应用方向。基于聚类的分割方法是一类很重要的图像分割方法。因此，本实验利用所提出的方法来分割如图6(a)所示的图像，并显示图像中主要目标物——花瓣，进而分析不同算法分割图像的效果。5种算法对图像的分割效果如图6(b)～图6(f)所示。从图6可以看出，本文提出的SDRFCM方法能较好地把花瓣分割出来，分类精度更高，视觉效果也较其他几个聚类算法更好，而其他4种算法的分割结果都存在“过分割”或“欠分割”现象。

(a) 原始图像 (b) FCM分割结果 (c) PCM分割结果

(d) FPCM分割结果 (e) FCMKL分割结果 (f) SDRFCM分割结果

4 结束语

聚类分析在数据挖掘、机器学习、图像处理等领域有着极为广泛的应用和研究价值，本文在C均值算法的基础上，引入了一种新的可用于模糊隶属度的正则化项，并针对传统聚类算法受异常点和噪声点影响严重的问题，给出了一种自动筛选样本点的策略，推导了算法的迭代公式。最后，通过模拟数据、实际数据以及在图像分割中的应用实验进一步验证了所提算法的有效性、准确性，其良好的聚类效果可进一步地推广到更多的领域中去进行知识的发现。