瓦斯抽采数据预处理技术及达标评判应用

吴克介,许 金，陈 清，张 翼

(中煤科工集团重庆研究院有限公司,重庆 400039)

0 引 言

矿井瓦斯安全事故严重影响和危害煤矿工作人员的生命安全，近年在贵州、四川和福建等地发生多起因抽采达标评判不符合规定擅自开采而引起的瓦斯事故。瓦斯抽采评判是预防矿井瓦斯安全事故的有效途径[1]，瓦斯抽采效果直接影响着矿井煤矿与瓦斯突出、瓦斯异常涌出、瓦斯爆炸等事故是否发生，应抽未抽或抽采效果不好都会导致发生事故的概率增大[2]。建立合理、完善的瓦斯抽采评判体系已成为当今煤矿企业加强瓦斯抽采力度，落实瓦斯抽采工作的重要途径[3-4]。

现阶段瓦斯抽采主要以人工评判为主，瓦斯抽采数据来源于人工测定与在线监测。人工测定的瓦斯抽采数据测定周期长，严重影响瓦斯抽采达标评判的准确性。在线监测设备没有应对因故障、断电等因素导致数据缺失问题的有效手段[5-7]。此外，人工评判存在程序复杂、计算繁琐、评判易出错等问题，导致评判结果不准确，产生潜在的安全隐患[8-10]。为了解决以上问题，部分学者研究瓦斯抽采评判系统[10-12]，以达到减少人力投入，提高工作效率的目的，如利用GIS技术实现煤矿瓦斯抽采过程的空间信息化管理，并通过分析抽采钻孔影响范围、钻孔瓦斯抽采量、钻孔影响参数范围内瓦斯参数、瓦斯抽采时间等多个参数变化规律，研究构建瓦斯抽采达标预测模型，对煤层残余瓦斯含量进行预测[13];利用瓦斯抽采数据、钻孔信息、瓦斯地址信息，对不同区段单位钻尺量的瓦斯抽采规律进行分析，通过选择邻近区域的瓦斯抽采规律，为决策者提供预评价区段的瓦斯储量、煤炭储量、预警施工钻尺量和抽采达标时间，实现抽采效果达标过程化管控[14]。这些系统在一定程度上提高了矿井瓦斯抽采达标评判工作效率，但未对评判数据源的数据质量进行校验，导致评判结果可靠性不高。

针对上述问题，本文研究瓦斯抽采时长与抽采累计量的关系，以《煤矿瓦斯抽采达标暂行规定》为理论依据，建立瓦斯抽采达标评判系统，对落实瓦斯抽采方案、简化人力投入、达到瓦斯预抽目的，具有非常重要的作用。

1 矿井现场情况分析

矿井工作面安装瓦斯抽采在线监测装置，与矿井监测系统联网，实时监控计量点的瓦斯抽采数据。

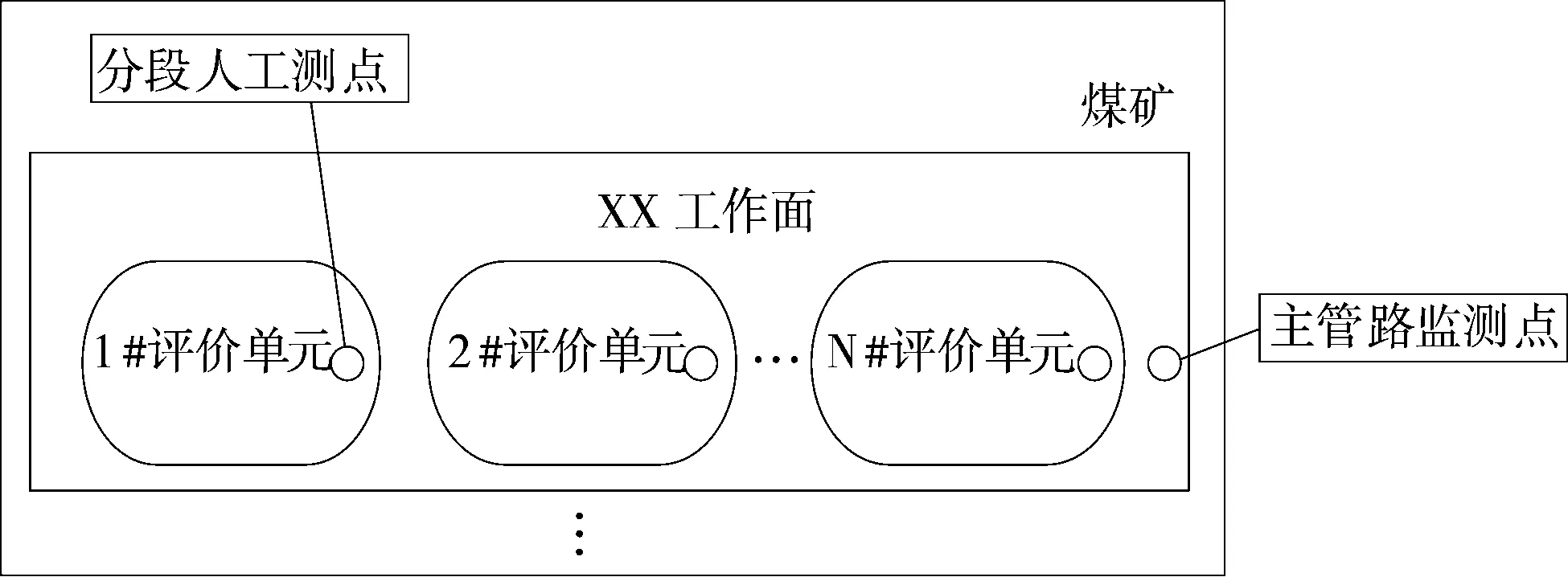
图1 瓦斯抽采达标评判工作面示意图

如图1所示，在煤矿的某个工作面上划分1#～N#评价单元，每个评价单元有矿井自主划分的分段人工测点，由测流员定期前往测定抽采纯量、抽采负压等信息，在工作面主管路上安装在线测流装置，实时监测工作面的总抽放量。

人工测量的瓦斯抽采数据周期长，无法为达标评判提供准确的数据源，影响评判结果的可靠性。在线计量装置能够提供准确、实时的瓦斯抽采数据，但无法应对断电、故障等非自然因素导致的数据缺失问题。

为了保障达标评判结果的可靠性，需要对达标评判的数据源进行预处理，主要解决以下问题：

1)人工测量数据粒度大，数据质量低。

2)在线计量数据缺失，不连续。

2 基于数据拟合的井下管道瓦斯监测值非连续采样插值方法

人工测量的井下管道瓦斯抽采数据准确性与真实数据之间的误差较小，可以将其看作不连续时间序列。以瓦斯抽采时长为自变量，累计瓦斯抽采量为因变量，某评价单元一段时间内的抽采时长与抽采累计量的关系如图2所示。

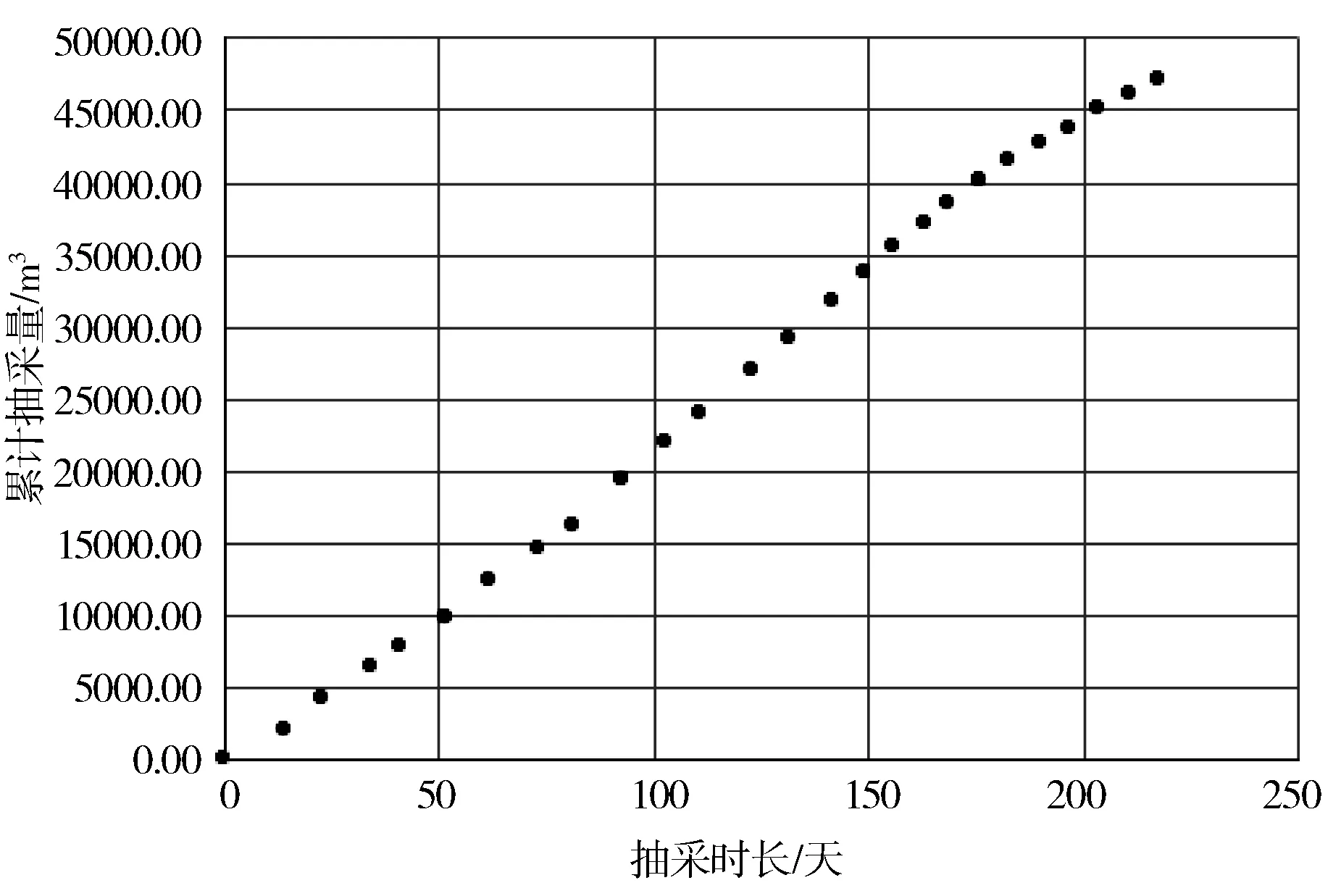
图2 抽采时长与抽采累计量的关系

由图2可知，抽采累计量与抽采时长成正比，二者之间是非线性关系，抽采时长与抽采累计量的关系可以用二维非线性函数关系式表述，求解抽采时长与抽采累计量的关系是非线性数据拟合问题。非线性拟合问题的核心是通过多次迭代获得最优的拟合参数，常用的最优化算法包括牛顿法、高斯牛顿法、Levenberg-Marquardt算法[15-16]。

根据人工测量的瓦斯抽采数据，可以构造n组抽采时长x(x1,x2,…,xn)与累计抽采量y(y1,y2,…,yn)组成的观测数据。

设工作面某评价单元的抽采时长x与抽采累计量y的非线性函数关系为:

y=f(x,b)+ε

(1)

其中，f为已知的非线性函数关系式，b为拟合公式的待定系数，由m个待估参数b1,b2, …,bm组成，ε为观测样本的测量误差。

将f(x,b)按照泰勒公式展开，略去二阶以上的无穷小：

f(x,b)=f(x,b0)+f′(x,b0)(x-b0)

(2)

f′(x,b)、f″(x,b)可以用雅可比矩阵与海森表示：

(3)

(4)

令f′(x,b)=0，则牛顿法的数据拟合迭代公式为：

(5)

非线性最小二乘法以估计值与实际值之间误差的平方和最小为准则来求解非线性方程中的参数估计问题。将式(2)作为最小二乘法的目标函数，记残差为：

ri(b)=yi-fi(x,b)

(6)

则最小二乘目标函数为:

(7)

令Q分别对b1,b2, …,bm求一阶偏导，可得：

(8)

将雅可比矩阵代入上式，则：

(9)

其中，bk代表第k个待估参数，bk为参数b的k次偏导数。

即：

(10)

则高斯牛顿法的迭代公式为：

bk+1=bk-(J(xi,bk)TJ(xi,bk))-1J(xi,bk)Tri(bk)

(11)

当J(xi,bk)TJ(xi,bk)奇异时高斯牛顿法无法继续迭代，莱文贝格-马夸特方法(Levenberg-Marquardt algorithm， LM)在高斯牛顿法的基础上添加了阻尼因子λ，将线性最小二乘问题转换为约束线性最小二乘问题[6]。

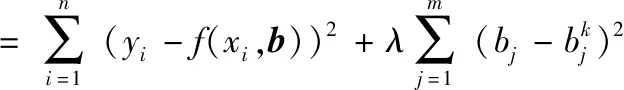
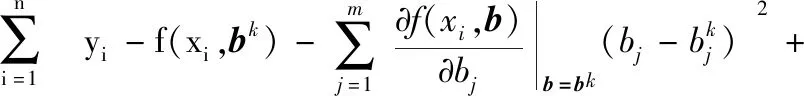
(12)

其中，λ≥0，为阻尼因子。

Q分别对b1,b2, …,bm求一阶偏导，可得：

(13)

将雅克比矩阵与海森矩阵代入上式，迭代公式为：

bk+1=bk+[H(x,bk)+λE]-1JT(x,bk)[y-f(x,bk)]

(14)

决定系数是衡量拟合效果优劣的指标，决定系数越大拟合效果越好：

(15)

基于数据拟合的井下管道瓦斯检测值非连续采样插值方法采用不同数据拟合算法对样本数据进行拟合，得出最优的抽采时间与抽采累计量的拟合函数，根据拟合函数对人工测量数据进行插值，具体步骤如下：

1)设置拟合算法最大迭代数、误差值、插值间隔等基本参数。

2)采用牛顿法、高斯牛顿法、Levenberg-Marquardt算法结合非线性拟合公式对观测数据进行拟合，选取决定系数最大的拟合公式作为抽采时间与抽采累计量的关系式。

3)根据抽采时间与抽采累计量的拟合关系式，按照插值间隔对观测数据进行插值。

3 在线计量瓦斯监测数据缺失值修补方法

在线计量瓦斯抽采数据缺失分为单点缺失与连续缺失2种情况。

针对在线瓦斯计量装置单点缺失问题，缺失数据点周围的数据完整性较好，采用滑动平均窗口法[17-19]修补缺失数据。假设观测数据为T{ti，i=1,2,…，n}，滑动窗口长度为H，缺失点tm的累计瓦斯抽采量修复值f(tm)为：

(16)

若瓦斯抽采数据存在连续多个抽采数据缺失点且时间跨度较大，数据的完整性较差，则无法直接通过数据拟合方法获得与瓦斯抽采数据相符的拟合曲线。

EM算法[20-23]是一种迭代优化策略，解决数据缺失情况下的参数估计问题，包括期望步(E步)和极大步(M步)。记Z为观测数据T中的缺失数据，则待估参数b的对数似然函数为：

L(b)=lnP(T,Z|b)

(17)

E步：根据观测数据T与待估参数初值bk，计算缺失数据Z的条件期望：

(18)

其中，P(Z|T，bk)是在观测数据X与参数估计bk下隐变量Z的条件概率分布。

M步：求使Q(b|bk)极大化的b确定第k+1次迭代的参数估计值：

bk+1=arg maxbQ(b,bk)

(19)

其中，Q函数指完全数据的对数似然函数lnP(T，Z|B)。

在线计量瓦斯监测数据缺失值修补方法步骤如下：

1)设置滑动窗口阈值、EM算法迭代参数初值、连续缺失长度阈值等基本参数。

2)以连续缺失长度阈值判断缺失数据的缺失类型，若为单点缺失，采用滑动平均窗口法修复缺失值。

3)若缺失数据为连续缺失，将未缺失的数据作为观测数据，采用EM算法对观测数据进行拟合，计算抽采时长与抽采累计量的关系模型。

4)根据第3步计算出的关系模型对连续缺失数据进行修补。

4 抽采达标评判系统

瓦斯抽采达标评判系统采用模块化开发，实现瓦斯抽采数字化管理与抽采达标在线过程化评判。系统面向煤监局与煤矿，采用矿端评判、局端监察评判结果的模式，在提高矿井瓦斯抽采达标评判效率的同时加强煤监局对煤矿瓦斯抽采达标评判工作的监督监察力度。抽采达标评判系统的功能结构如图3所示。

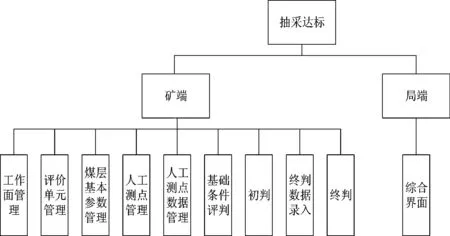
图3 抽采达标评判系统功能结构图

评判数据源由煤矿安装的在线测流装置与便携式测量仪自动采集，经过数据预处理后接入系统。系统以《煤矿瓦斯抽采达标暂行规定》为理论依据，自动对评价单元的划分合理性、抽放泵站装机能力、残余瓦斯含量、残余瓦斯压力、瓦斯抽采率、风速、回风流瓦斯浓度等指标进行评判。具体评判流程如图4所示。

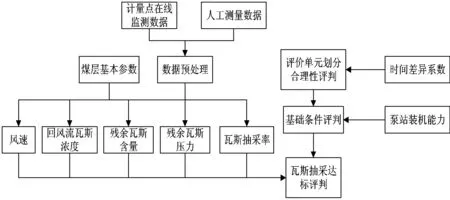
图4 抽采达标评判系统评判流程

5 工程应用及效果检验

5.1 矿井概况

重庆渝新能源公司石壕煤矿位于重庆市綦江区石壕镇，待评价工作面为N1633工作面，属于M6-3煤层，灰黑色，半亮型煤，金刚光泽，性脆，易成鳞片状及粉末状，含黄铁矿。煤厚0.81～1.05 m,平均为0.93 m，原始瓦斯含量为12.56 m3/t，大于8 m3/t，有突出危险。矿井瓦斯抽采计量采用在线智能监控计量和人工皮托管计量2种方式，在线监测数据与人工测流数据作为抽采达标评判的基础数据。

5.2 人工测量数据拟合效果检验

N1633工作面北回风巷分为3段，第一段含有34个抽采钻孔，第二段含有15个抽采钻孔，第三段含有33个抽采钻孔。采用牛顿法、高斯牛顿法、Levenberg-Marquardt算法对N1633工作面第一段2019年1月-2019年6月的人工测量数据进行拟合，根据决定系数衡量拟合算法，拟合结果如表1所示。

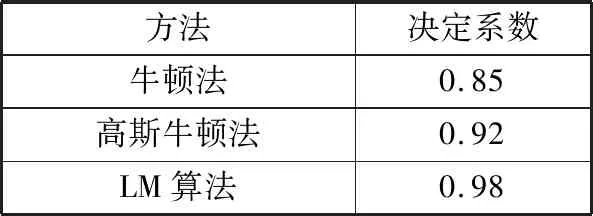
表1 数据拟合决定系数对比

由表1可知，LM算法拟合的决定系数较高斯牛顿法提高0.06，较牛顿法提高0.13，下面阐述这3种算法的具体拟合曲线表达式及拟合参数，拟合曲线如图5～图7所示。

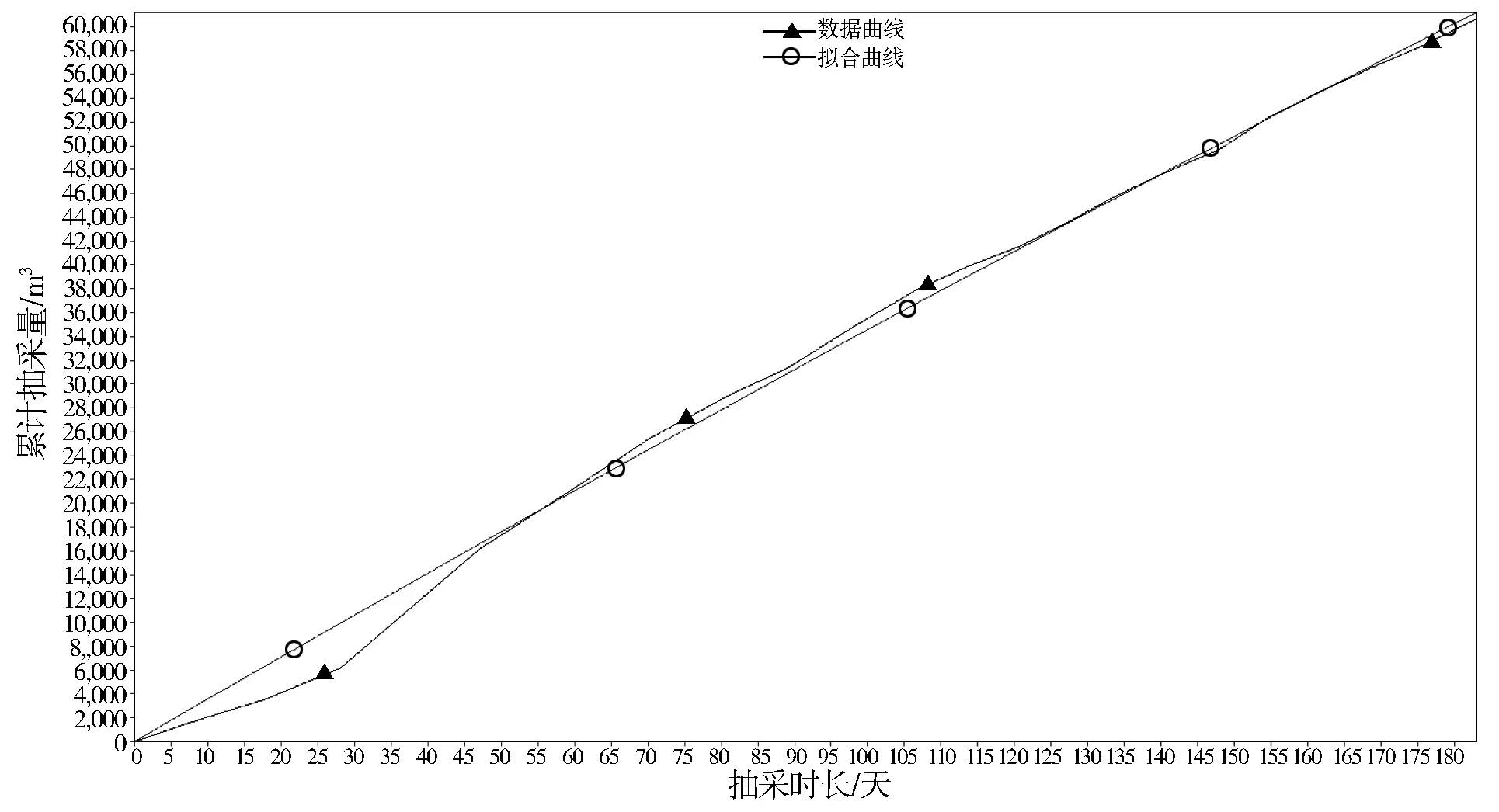
图5 牛顿法拟合曲线

牛顿法拟合曲线表达式及参数如下：

(20)

其中，p1=399900，p2=-402028，p3=986。

图6 高斯牛顿法拟合曲线

高斯牛顿法拟合曲线表达式及参数如下：

(21)

其中，p1=1.15×10-6，p2=0.0027。

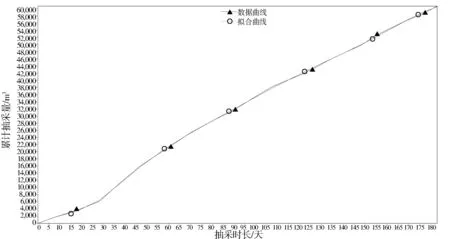
图7 Levenberg-Marquardt算法拟合曲线

Levenberg-Marquardt算法拟合曲线表达式及参数如下：

(22)

其中，p1=-789.92，p2=3097.82，p3=-3228.2，p4=1591.89，p5=-442.17，p6=75.8，p7=-8.34，p8=0.59，p9=-0.02，p10=6.5×10-4，p11=-7.18×10-6。

5.3 在线计量数据修复效果检验

采用N1633主干网在线计量设备2019年1月-2019年3月的瓦斯抽采数据作为实验数据，对数据按0.05、0.1、0.2、0.4的缺失比例进行随机缺失，采用滑动窗口算法、EM算法、滑动窗口算法与EM算法相结合的算法分别对缺失数据进行修复，通过均方根误差RMSE(Root Mean Square Error)、修复时间2个指标衡量算法的修复效果。

(23)

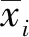
记滑动窗口法、EM法、滑动窗口+EM算法对数据修复的均方根误差分别为RMSE1、RMSE2、RMSE3，修复时间分别为t1、t2、t3，数据修复结果如表2所示，修复时间对比结果如表3所示。

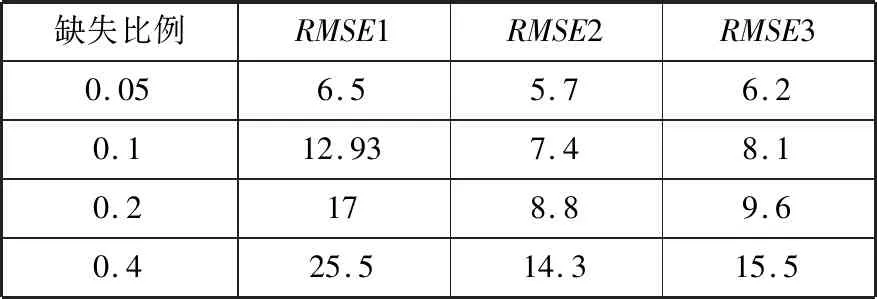
表2 数据修复均方误差对比 单位：%

表3 数据修复时间对比 单位：s

由表2可知，3种算法的均方误差由低到高依次为EM算法、EM算法与滑动窗口法相结合的算法、滑动窗口算法。EM算法修复数据的均方误差均值较EM算法与滑动窗口法相结合的算法均方误差均值降低3.9%，较滑动窗口法均方误差均值降低26.43%。

由表3可知，3种算法的运行时间由高到低依次为EM算法、EM算法与滑动窗口法相结合的算法、滑动窗口算法。滑动窗口算法平均修复时间较EM算法与滑动窗口法相结合的算法平均修复时间降低25%，较EM算法平均修复时间降低74%。

综合考虑修复结果的RMSE与修复时间，EM算法与滑动窗口性能最佳，能够在较短的时间内修复瓦斯监测缺失值。

5.4 达标评判效果检验

N1633工作面的具体参数如表4所示。

表4 工作面参数

根据《煤矿瓦斯抽采达标暂行规定》，待评判工作面的残余瓦斯含量小于8 m3/t或者残余瓦斯压力小于0.74 MPa，风速与回风流瓦斯浓度分别小于4 m/s、1%时，该工作面瓦斯抽采达标。N1633工作面的评判结果如表5所示。

表5 N1633工作面评判结果

综合以上所有评判结果可得出，石壕煤矿N1633工作面瓦斯抽采的评判结果为达标，可以安全进行下一步工作。

6 结束语

本文通过研究瓦斯抽采时长与抽采累计量的关系，解决了人工测量数据质量低、在线计量点瓦斯抽采数据缺失的问题。在此基础上设计并实现了瓦斯抽采达标评判系统，实现了抽采数字化管理与在线过程化评判，提高了矿井瓦斯抽采评判效率，降低了人工评判不准确的潜在风险。工程应用结果表明，系统评判结果与实际相符。由此可见，瓦斯抽采评判系统在一定程度上减少了人力、物力、财力的投入，具有较好的推广前景。