快速挖掘最大频繁项集算法在图书馆管理中的应用
于海洋
(核工业理化工程研究院,天津 300180)
0 引 言
图书馆作为高校师生情报数据库的第一手来源,珍藏着涉及广泛学科的丰富图书,并且每年都会购进新书,这使得图书馆馆藏图书的规模也越发庞大。截止2018年,清华大学图书馆馆藏图书共525.5万册;北京大学图书馆馆藏图书共1100余万册;浙江大学图书馆馆藏图书共623.5万册[1]。为大学老师和学生从成千上万的藏书中找到他们所期待的图书成为一项艰巨的任务。随着高校图书馆数字资源的存储海量化,数据类型非结构化,读者访问持续性、高并发性以及云计算与云存储、大数据等新技术在高校图书馆中逐步应用,庞大的存储量对于发现其内在的规则也是一个巨大的挑战。因此,如何对库存图书的结构进行准确而有效的优化,对于教师和学生的学习和研究具有重要的意义。
用户对图书馆的需求不同,加之各种现代化技术的进步使得用户个性化需求变得更加明显,图书馆要满足用户日益凸显的个性化需求,必须转变服务方式。转变图书馆的服务方式主要是转变基于信息用户的信息使用方式,通过挖掘用户的搜索数据,找出用户感兴趣的图书及内在的关联规则[2],有目的、有针对性地订制图书,可以有效缓解供需矛盾的现状。挖掘频繁项集是数据挖掘中的重要且基本的问题,通过计算事务数据库中称为项目集子组的出现来查找频繁的项目集。由于频繁项目集中包含的项目同时发生的可能性很高,因此可以从频繁项目集中了解项目之间的关系。从该技术获得的知识已广泛用于数据分析,例如传感器网络、网络流量、股票市场和欺诈检测的分析。挖掘频繁项集[3-4]和关联规则是在大型数据库中发现变量之间有趣关系的一种流行的、经过深入研究的方法。
1 方法简介
1.1 频繁项集、超集、最大频繁项集与直接真包含
项的集合称为项集,包含k个项的项集称为k-项集。项集的出现频率是包含项集的事务数,简称为项集的频率,用支持度计数。项集出现的频率称为相对支持度。设I为一个项集,若I的相对支持度满足预定义的最小支持度阈值,则I为频繁项集。
若一个集合S2中的每一个元素都在集合S1中,且集合S1中可能包含S2中没有的元素,则集合S1就是S2的一个超集。S1是S2的超集,则S2是S1的真子集,反之亦然。
设X为一个频繁项集,如果X的任意一个超集都是非频繁的,则称X是最大频繁项集,记为MFI(Maximal Frequent Itemsets)。
设t是属性A上的事务集,对t的直接真包含实子集中的一个子集,如果该子集的元素在属性ai上的子集均为t在属性ai上的子集的真子集,且t的直接真包含子集所有具有该性质的元素均在该子集中,则称该子集为t在属性ai上的直接真包含子集。
推论1 如果X不是频繁项集,则X的所有超集都不是频繁项集;类似地,如果X是频繁项集,则X的全部非空子集都是频繁项集。
推论2 在布尔矩阵中,如果行向量中1的个数小于最小支持度,则此行可删除。
证明:根据频繁项集的推论可知:频繁项集的全部非空子集都是频繁项集。在布尔矩阵中,1代表该事务中存在该项,1的个数则表示该事务中包含的项数。在求k-项集时,由于1的个数k小于最小支持度min_sup,得出的项是非频繁项集,与频繁项集无关,故此行可以删除。
1.2 关联规则
关联规则需要同时满足最小支持[5-7]和最小置信约束。在中等或较低的支持值下,数据库中通常会发现大量的频繁项集。然而,由于支持的定义强制要求频繁项集的所有子集也必须是频繁的,因此只挖掘所有最大频繁项集就足够了,频繁项集不是任何其他频繁项集的子集。另一种减少挖掘项集数量的方法是只挖掘频繁闭项集。如果在包含itemset的每个事务中不包含itemset的适当超集,则关闭itemset。频繁闭项集是最大频繁项集的超集。它们相对于最大频繁项集的优势在于,除了生成所有频繁项集之外,还保存了所有频繁项集的支持信息,这些信息对于挖掘过程结束后计算额外的兴趣度量是非常重要的。
设I={i1,i2,…,im}是项的集合,D是数据库事务的集合,其中每个事务T是项的集合,使得T为I的子集。每一个事务有一个标识符,称作TID。设A是一个项集,事务T包含A当且仅当A是T的子集。关联规则形式是:A⟹B,其中A、B是I的真子集,并且A∩B=∅。规则A⟹B在事务集D中成立,是指其支持度S不小于给定的最小支持度,其中支持度S是D中包含A∪B的事务数与D中事务数之比。规则A⟹B在事务集D中具有置信度C,指D中包含A∪B的事务数与D中包含A的事务数之比。
支持度:如果事务集D中数据同时满足A和B的百分比为S,则称规则A⟹B具有支持度(Support)S。
计算公式:
(1)
置信度:如果事务集D中满足A的数据中有百分比为C的数据同时满足B,则称规则A⟹B在数据库D中的置信度(Confidence)为C。
计算公式:
(2)
1.3 挖掘算法
图书馆的图书种类是一个多维数据,根据《中国图书馆分类》的22大类中的英文字母表示,如F表示经济类,H表示语言、文字类,I表示文学类,K表示历史、地理类,T表示工业技术类,Z表示综合图书等,在挖掘中,可以将每一个类当做一个维度。在每一个维度内,又包含很多的分类,这些分类在本文中不作考虑。在对图书种类进行挖掘时,要考虑到维内与维间[8-9]2个方面。
利用ILASii系统从图书馆管理系统中获取用户的借阅记录及图书信息等数据,将这些数据存储在数据仓库中,结合联机分析处理技术形成多维数据立方体[5]。
1.3.1 DS-Eclat算法
DS-Eclat算法[10-12]是一种基于深度优先算法的垂直数据表示方法。DS-Eclat算法是在Eclat算法基础之上,将事务集映射到布尔矩阵中,根据布尔矩阵[13-16]中的标志位得到事务项的支持度数,进而对数据库根据支持度的大小进行分割,优先选择对支持度大的项目集进行运算,减少无用数据对挖掘效率的影响,该算法使用回写集和深度搜索最长项集2项新技术,在每次迭代中,无须扫描整个图书馆数据库,对于(K+1)项集的搜索仅依赖于K项集,并生成K项回写集,下一次迭代时吸取这些回写集,减少了交运算的次数,提高了算法的执行效率。
传统的Eclat算法没有实现关联算法的先验性质[17-18],也就是说,任何频繁项集的所有非空子集也必须是频繁项集,而任何不频繁项集的父类也是不频繁项集。本文对Eclat算法的改进主要是通过减少自连接交叉口频繁项集生成的候选集数量来减少运算时间。DS-Eclat算法由广度优先(BFS)改进而成,类似于层次遍历。广度优先算法是一种图形搜索算法,从根节点开始,根据层次结构逐层访问其他节点。首先,访问根节点到K的所有邻居,并标记访问权限,然后继续访问与这些邻居距离(K+1)的其他节点,以此类推,直到找到目标为止,算法结束。与使用循环的depthfirst实现相比,DS-Eclat算法可优先使用队列,减少了操作时间,并且提高了操作效率。
1.3.2 频繁项算法模型
在数据模型中,定义(K,τ)为频繁项,D为数据库。若元素i是频繁项,则i必将满足公式(3)。在公式(3)中,W为符合数据库D的所有实例构成的集合,K是数量阈值,mi是元素i出现的次数,τ为概率阈值。
(3)
数据库D中的频繁项的确定需要将数据库中的所有可能实例进行检测,通过公式(3)进行计算,可能实例检测元素的数量呈指数级增长,具有不可行性,需要进一步过滤处理以减少检测次数[19]。
数据流可以分成数据流和不确定数据2个部分,不确定数据在连续、无限的数据流中并不是均匀分布的,不确定数据会影响挖掘的结果,它会随着时间的推进而变化,这为数据频繁项集挖掘提出了巨大的挑战。并且由于数据流的流速快、数据量大,传统上在运行数据频繁项集挖掘算法时,容易造成内存空间占用过大,系统出现卡顿现象,降低挖掘性能,因此通过加入深度玻尔兹曼机,可以提高挖掘效率,减少内存中的维护频繁项集数[20-23]。
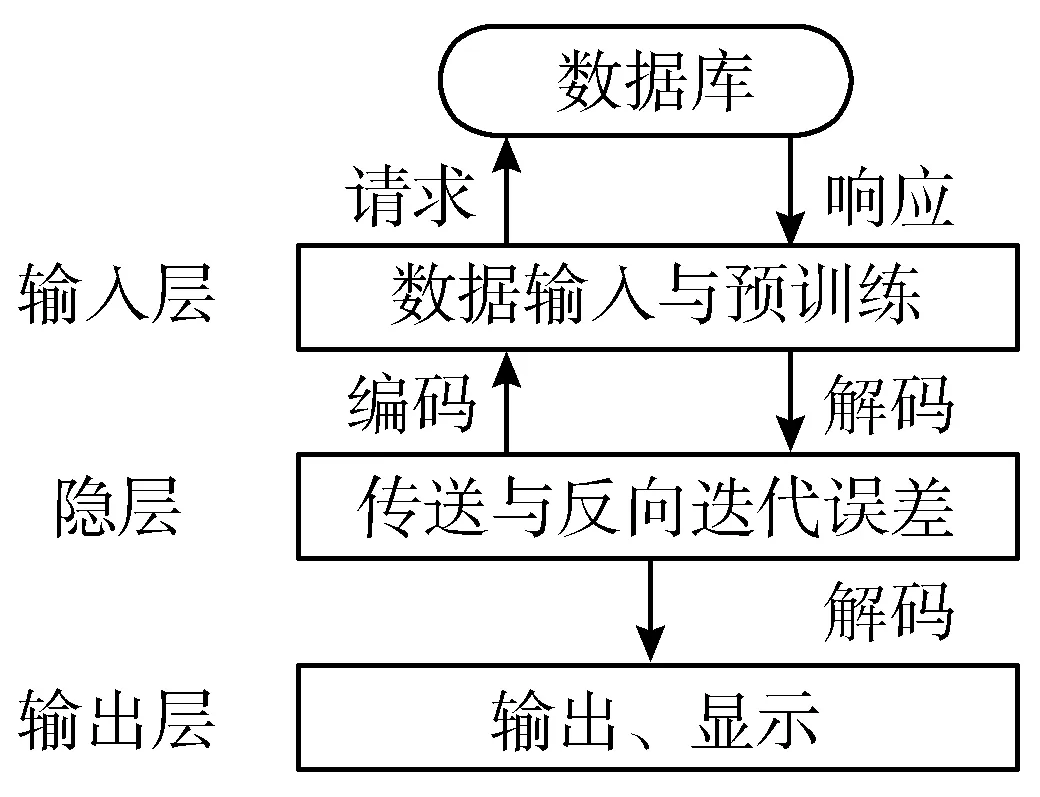
图1 频繁项算法流程图
如图1所示,将每层的输入信号与权值进行计算生成进一步信号传递到下一层,将信号再次与权重进行计算,将生成的重构信号进行映射,传回输入层,与原始信号进行比较,分析并减少误差,达到训练每层网络的目的。在预训练完成过程中完成对信号的编解码重建过程,反向迭代误差提高系统的精密度。
2 DS-Eclat算法设计与分析
2.1 DS-Eclat算法流程设计
1)从数据立方体中选定一个维,将这些数据映射到布尔矩阵Di×(j+1)中,其中第(j+1)列为标志位,初始均置为0。循环遍历,对标志位Di,j+1进行加运算。当Di,k=1时,Di,j+1=Di,j+1++,该行遍历结束时,Di,j+1为该行1的个数。
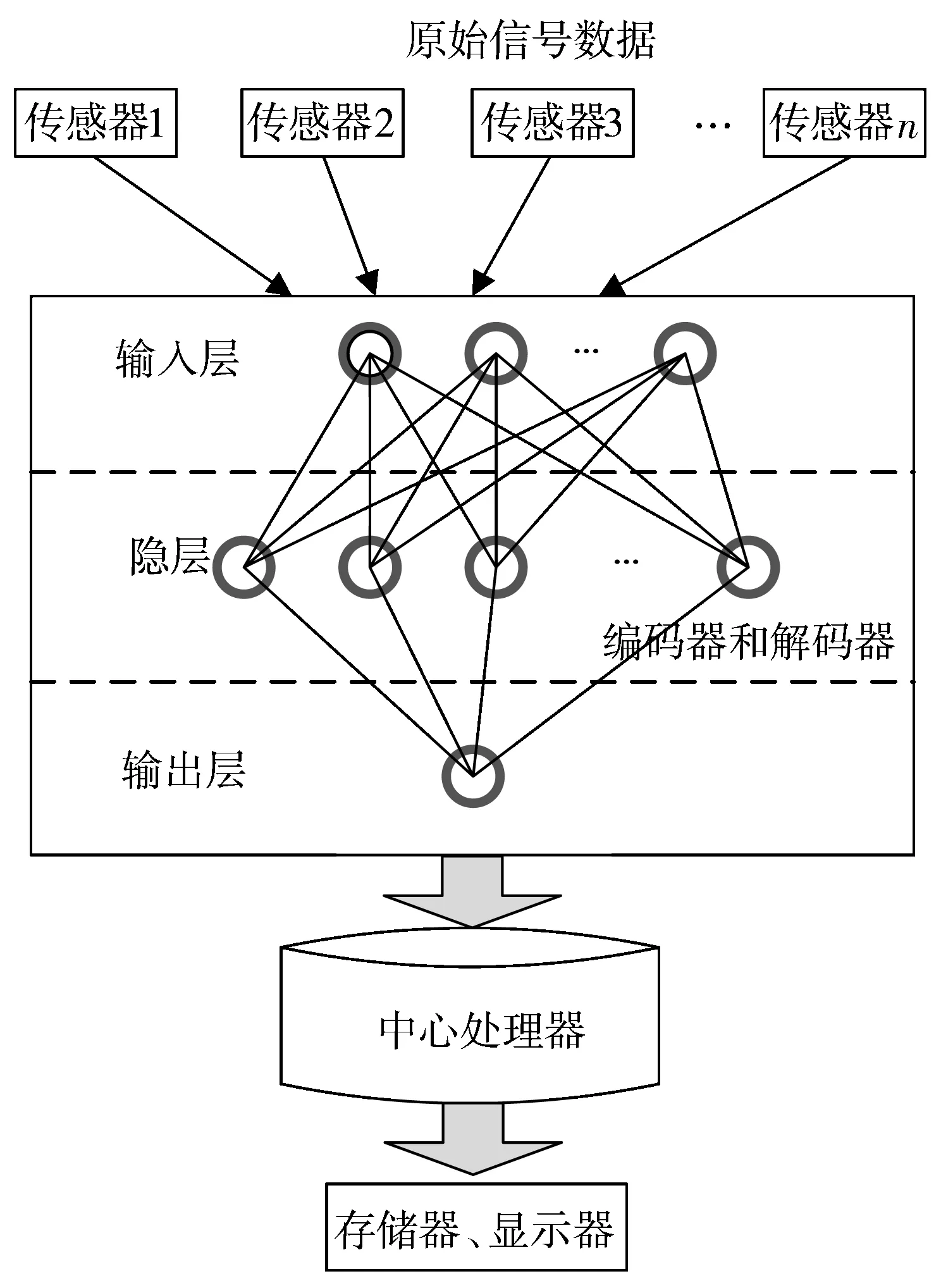
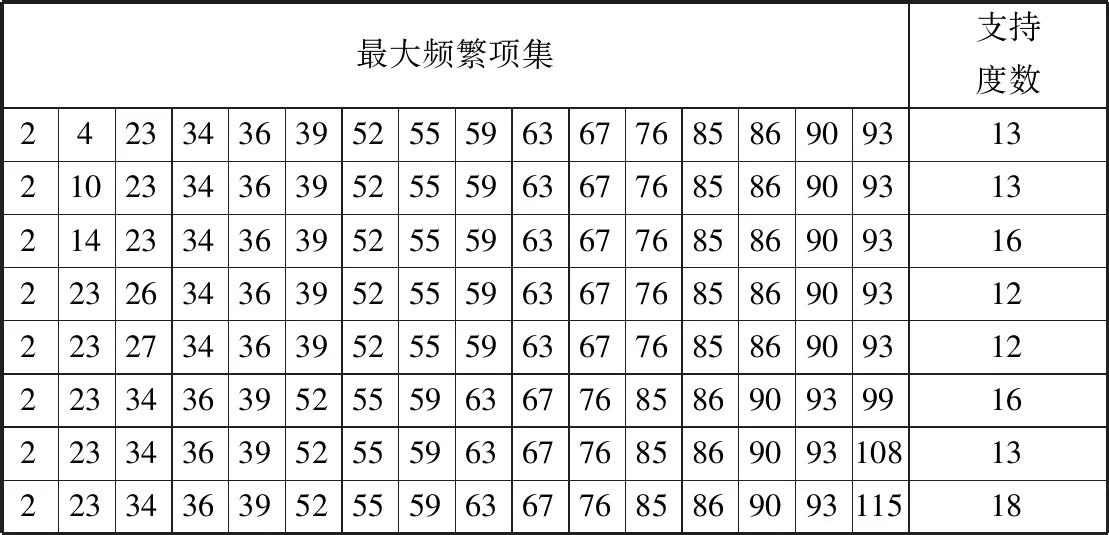
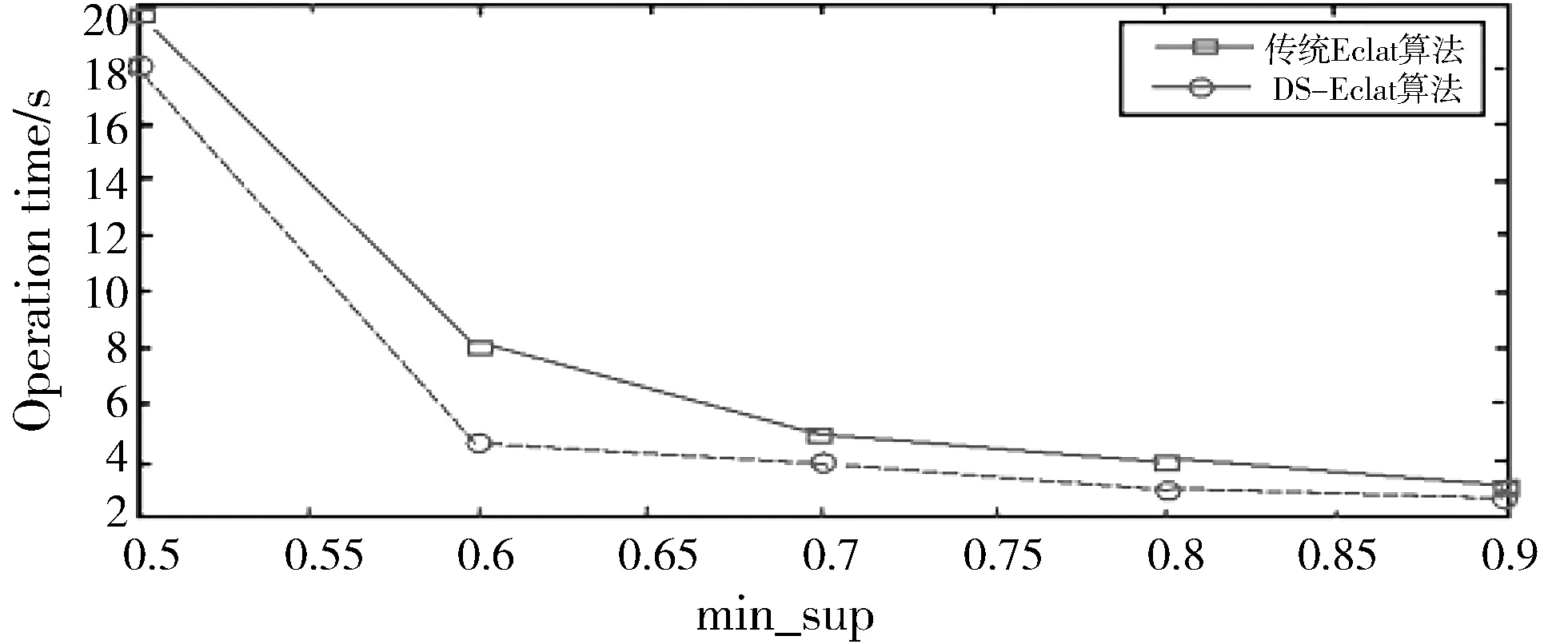
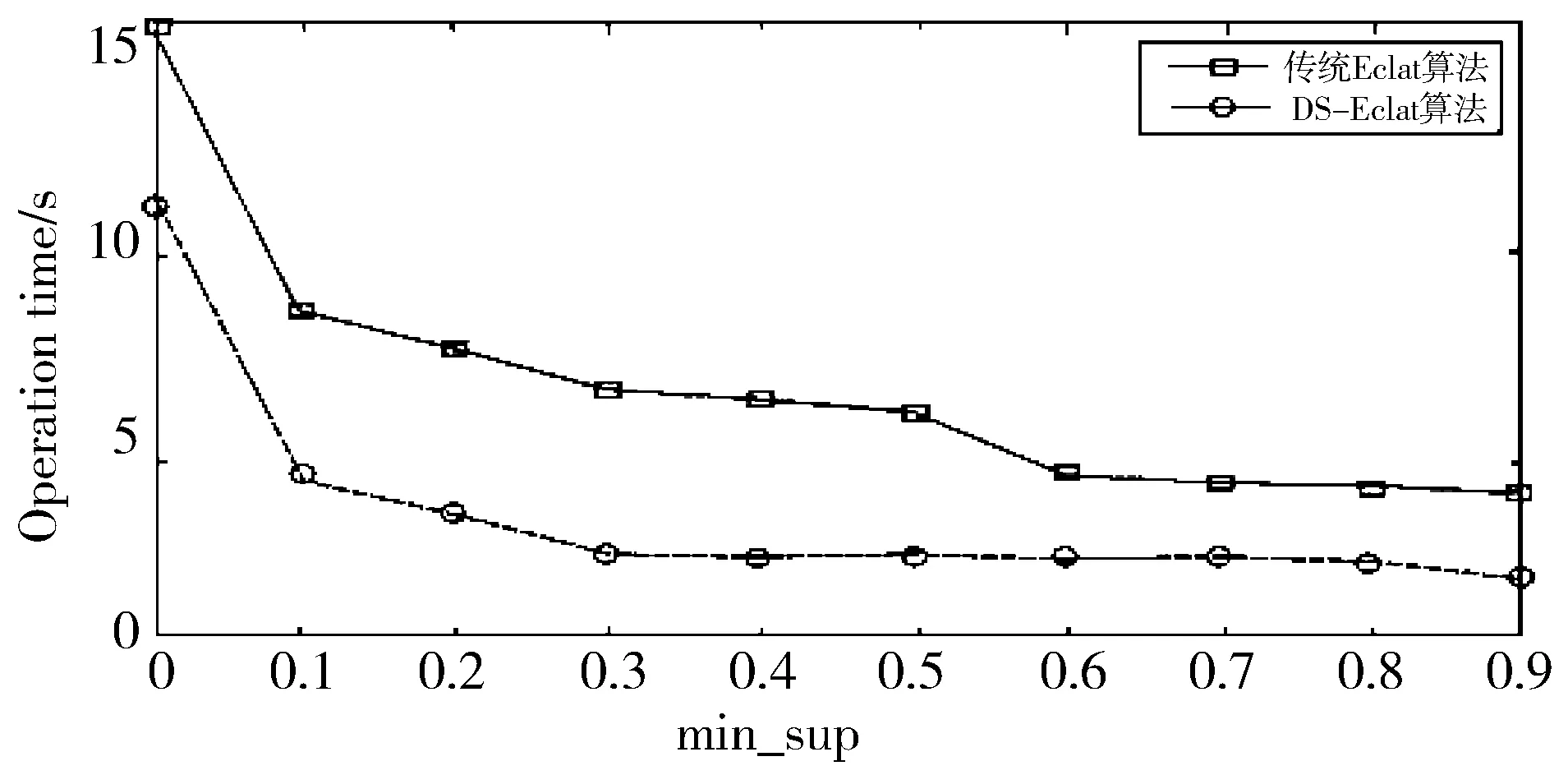
2)根据标志位对数据集进行重新排列,按降序排列,根据推论2,删除Di,j+1 3)对D′ij进行分割。根据候选最大频繁项集和事务集的大小来选定参与计算的对象。通过仿真验证得出,选取对象为D′ij的总行数的1/7。在验证试验中,以1/7为数据分割点得到的最大频繁项集的准确度为96.5%。因此,可以将33%作为数据集的分割点,即D′ij被分为d1,d2,…,d6,d7共7个部分。 4)根据设定的最小支持度,来判断运算结果是否满足最小支持度。若d1的运算结果满足条件,则运算结果记为l1,l′1=0,否则,l′1=l1,l1置0;然后顺次对d2,d3,…,d6,d7进行计算,运算结果记为l2,l3,…,l6,l7及l′2,l′3,…,l′6,l′7;若l1,l2,…,l6,l7均为0,那么最终结果L′=l′1∪l′2∪…∪l′6∪l′7;否则最终结果为L=l1∪l2∪…∪l6∪l7。 算法流程图如图2所示。 图2 DS-Eclat算法流程图 图3 快速挖掘最大频繁项集系统硬件设计 如图3所示,用多个传感器针对不同类型的数据集进行采集,将收集到的数据经由深度学习神经网络,按照每一项集的概率不同将不确定数据库分裂为多个概率项集,完成对数据的预处理、分类、再经由中心处理器将不确定数据频繁项集进行挖掘。 最后出现外部设备存储器和显示器将所有流数据和最终挖掘到的精确的不确定数据频繁项集进行存储和显示。在系统进行频繁项集挖掘过程中,计数和交集操作是计算项集支持度的主要方法,支持度的计算关系到系统的实际工作效率,各项的预期支持度应介于0~1之间。 多维数据的挖掘主要分为维内挖掘与维间挖掘[24],本文主要讨论维内挖掘。维内挖掘主要是针对在一特定维度内,数据间存在的关联规则。通过对维间关系的挖掘,找到其内在的关系,根据这些关系改善图书馆现在的服务方式,提高图书馆的运作效率。 维内挖掘主要是分析用户在一个维内对哪些东西感兴趣,挖掘出维内的关联规则,促进图书馆对特定种类的图书在结构上进行改进,同时促进图书馆服务方式的改变。 在仿真中,挖掘对象采用实验数据集来模拟图书馆用户的搜索信息。 DS-Eclat算法采用Java编程,仿真平台是联想G450,Win7系统,2.0 GHz CPU,2.0 GB的内存。仿真数值设定:S=0.25,C=0.5。Mushroom数据集为仿真对象,共采集500位用户的搜索信息,根据数据集,设定每人搜索了23本图书。 仿真结果如表1、表2所示。 表1 维内最大频繁项集及其支持度数 表2 维内1-项集统计 根据表1及表2可以得出,表2中的图书是这500名用户搜索的结果总计,根据图书名依次排列,表1是满足设定的支持度和置信度的图书,结合2个表可以发现,最大频繁项集中的各个元素都是在表2中支持度很高的元素,图书馆可以根据这一挖掘结果调整图书订制结构,适度增加相应图书的购买量。同时,根据表1,最大频繁项集中的各个元素彼此之间有较强的关联规则,根据最大频繁项集可以更好地分析用户的兴趣、习惯及特点,跟踪用户的兴趣变化模式,发现用户的最新需要;根据用户的兴趣,提供相应的预测报告、动态分析等。这有利于图书馆的服务模式由被动转为主动,图书馆可以根据用户的需求,主动地提供个性化的服务,从而提高图书馆服务用户的能力,也有利于提高用户的积极性。 通过比较传统的Eclat算法与DS-Eclat算法,验证DS-Eclat算法的有效性。由于实验的需要,数据集分为2类:密集数据集和稀疏数据集。其中,密集数据集包含某高校2013-2017年图书馆科技类图书的借阅信息,稀疏数据集包含2016-2017年科技类图书的借阅信息。实验平台为PC(Intel i3, CPU 2.30 GHz,内存4 GB),操作系统为Win7 Ultimate。在实验操作的过程中,结果显示一定程度的偏差,为了避免非过程化因素对实验结果的干扰,这个实验需要一些实验操作的平均值作为算法运行时间。由于集合数据集的密度不同,选择相应的支持阈值进行实验,便于比较实验操作。图4、图5分别为密集数据集和稀疏数据集的比较实验。 图4 密集数据集实验对比图 图4显示了支持阈值为50%~90%的实验对比图。结果表明,当支持度较大时,2种算法的运行时间趋于接近;当支持度较小时,2种算法的运行时间差较大,当min_sup为0.6时,DS-Eclat算法比传统Eclat算法运行时间减少10.6个百分点;当min_sup为0.8时,DS-Eclat算法比传统Eclat算法运行时间降低2.4个百分点。 图5 稀疏数据集实验对比图 图5显示了支持阈值为0~90%的实验对比图。结果表明,DS-Eclat算法运行时间短,速度快。当min_sup为0.5时,改进的DS-Eclat算法运行时间比原算法至少减少了12.5个百分点。从图5的实验结果来看,DS-Eclat算法的运行效率略优于Eclat算法。特别是当数据集较松散,支持度较低时,DS-Eclat算法更有效。 随着信息时代的到来,图书馆的传统服务方式日益跟不上用户的需求,个性化的信息服务愈发显得重要。本文提出了快速挖掘最大频繁项集的算法,并将其应用于图书馆管理,使用DS-Eclat算法的维内挖掘技术,分析用户的兴趣、习惯及特点。通过与传统的Eclat算法相比较,验证了DS-Eclat算法的有效性。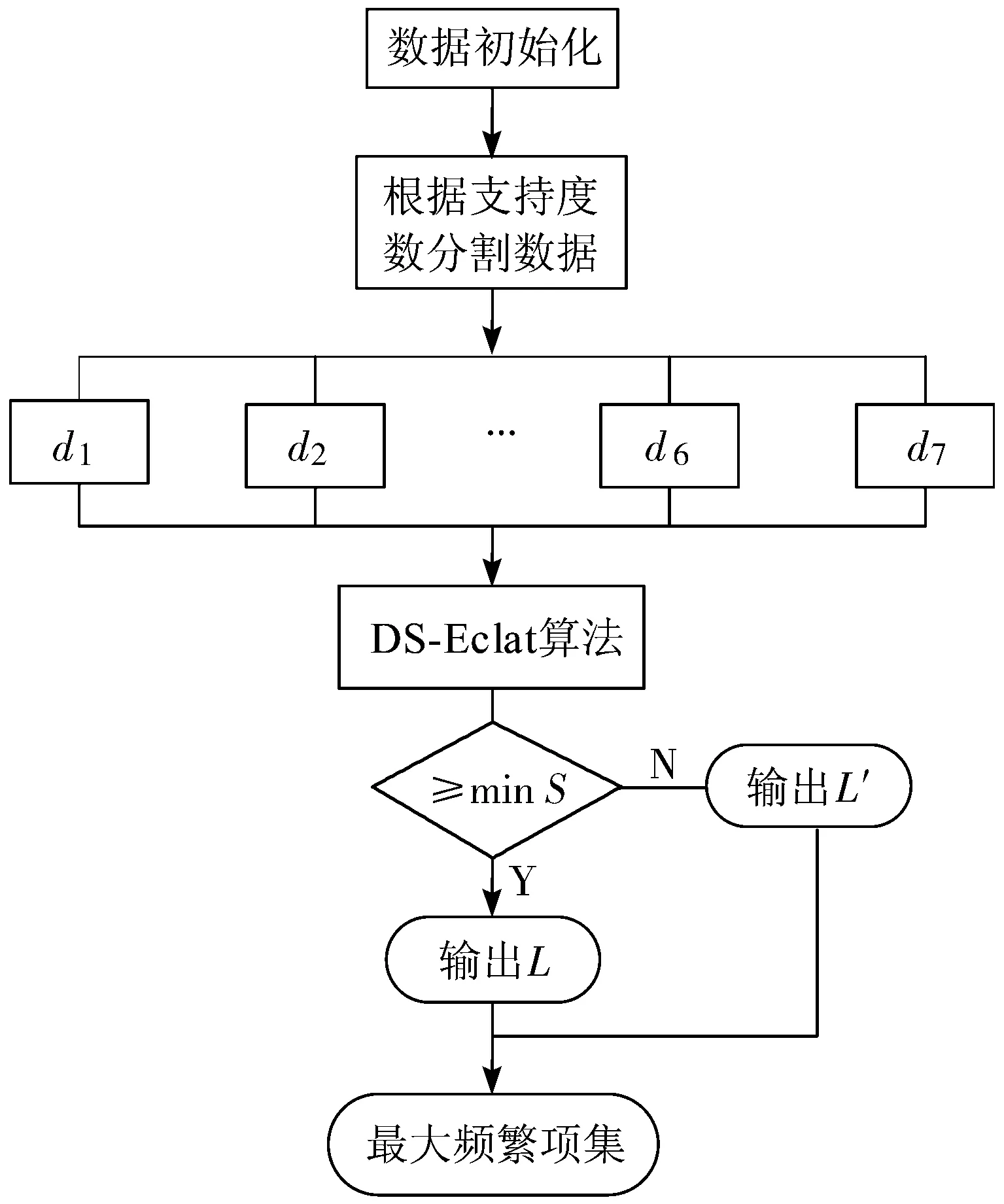
2.2 硬件设计
2.3 维内挖掘分析及仿真

3 实验验证
4 结束语

