基于模块化多尺度算法的通信重叠社区检测

蒋智恩

(福建信息职业技术学院 商贸管理系，福建 福州 350003)

一般认为，社区是一些连接更为紧密的节点集合。现实世界中许多网络都具有社区特性，比如通信网络、社会网络、计算机网络、神经网络、蛋白质网络等。为了分析这些复杂网络的拓扑特性及结构功能，对其进行社区检测很有必要。

实际网络中更为常见的是社区重叠的情况，即一个节点同时被多个社区共享。近年来学者们提出一系列相应的启发式算法。Palla提出了CPM算法[1]，算法认为一个社区内节点间的边可形成全联通图(clique)，通过相互连通的k-团来发现社区结构。Lancichinetti[2]提出了LFM算法，该算法的基本思想是通过目标函数的直方图峰值区分社区。Steve等人[3]在GN算法的基础上提出了CONGA算法，该算法将部分节点分裂成多个子节点，之后利用GN算法来处理，但其时间复杂度很高。基于矩阵因式分解的方法也可用于重叠社区检测，并扩展出很多新算法，例如Psorakis等[4]和Wang等[5]提出的NMF算法，但是NMF所涉及的数据矩阵通常存在缺失值。目前关于社区结构的多尺度特征研究还很少，陈东等[6]基于结构相似度提出了多尺度局部社区发现算法，引入尺度分子来定义结构模块度，在局部社区检测中得到了良好的效果。郭玉泉等[7]则将谱分析与启发式遗传算法相结合，提出多尺度社区检测算法HGASA。

基于以上研究，尝试提出一种模块化多尺度通信重叠社区检测算法，从单个节点、单个社区以及整个网络的尺度上，量化各种尺度下社区结构特征，合并在一起组成算法内容。最后通过实验验证不同尺度下各类参数对检测效果的影响，并在现实世界网络中检验算法有效性和准确性。

1 模块化多尺度算法

为了完整描述社区特性，需要解决社区定义的多尺度问题：单个节点的尺度、单个社区的尺度、整个网络的尺度。算法功能：针对社会网络中社区重叠问题，尝试从尺度特征出发提出合理的解决方法。对于一个给定的待检社区，根据每种尺度的社区结构调整具体的量化模块，因此，提出的方法是高度模块化的。这种方法为探索社区检测算法提供了一种新思路，符合目标社区检测要求。多尺度社区结构反映了在传播过程中的网络动力学特征，可以有效地揭示出网络的社区结构。

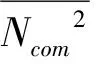
输入：网络的邻接矩阵

算法：

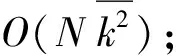
③ 如果社区中有节点未被聚类，将它们添加到与他们连接最频繁的社区。成本：可忽略；

④ 剔除检测出的更小的社区，规定所有的节点至少属于一个社区，描述方法见1.3节。

输出：网络中节点集组成的社区。

1.1 社区结构的节点尺度特征

由于算法的出发点是从边的排列中识别社区，这里把描述社区结构的节点集称为边缘描述符集。一个节点所属的连通图都可由边缘描述符集产生。

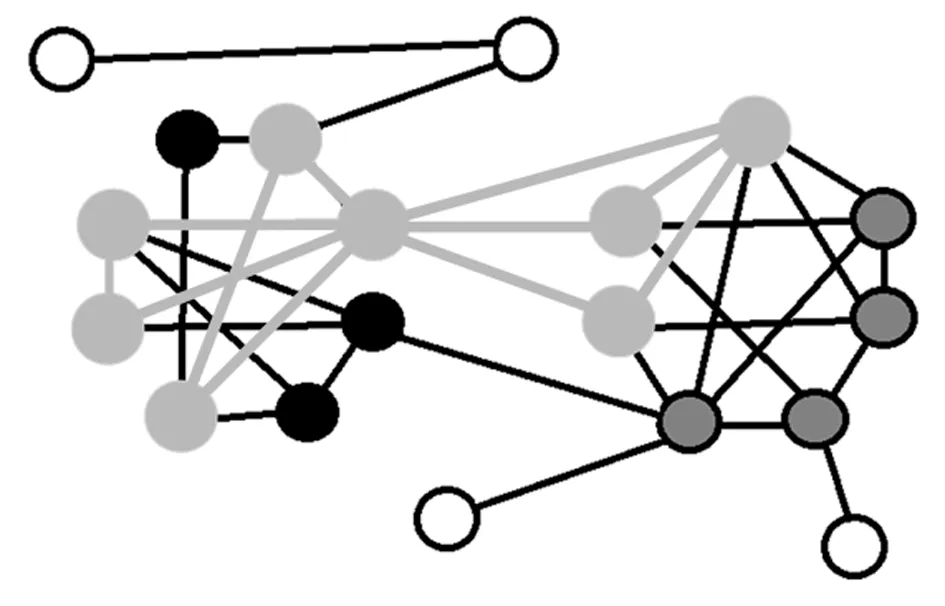
图1 网络中星标节点的自我中心网

假设一个节点与某个社区内其他节点有更密切的联系，那它属于这个社区的可能性就更大，这说明同一社区内节点间的边连接更加密集。因此，一个由边集合组成的连通图可看作是一种边聚类的原型。同时，当一个节点属于几个相对较大且不相交的连通图时，这个节点可认为是多个社区间的交点。在以上社区形成规则的基础上，提出提取边集的方法，其中，这些边集不仅连接紧密，而且大部分彼此不相交，每个节点的自我中心网(egonet)可认为是该节点的边缘描述符集，如图1所示，所有的浅灰和浅灰边都属于星标节点的自我中心网。每个集合可看作是社区结构小尺度特征的一组编码。

1.2 社区结构的社区尺度特征

边缘描述符集被提取出来后，需要一种集中现有局部特征共同形成社区的方式。为此，使用和社区尺度相关的量化特征来聚类这些边集。

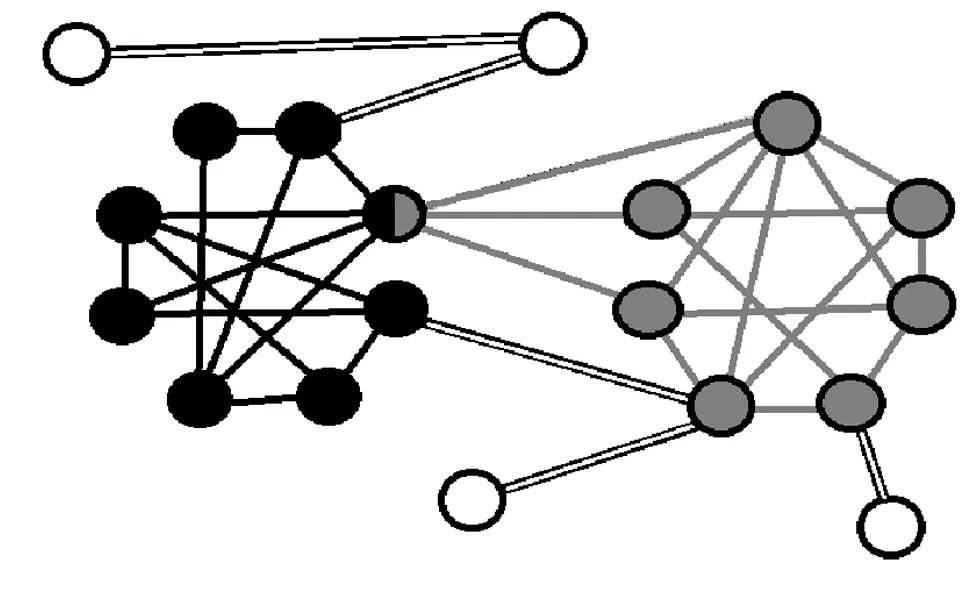
图2 黑色社区、灰色社区的分布

一个待检测社区拥有的总体量化特征，就是它们具有比整个网络更高的边密度，这一特点也可以在单个节点的边缘描述符集上清楚地显现出来。网络示例如图2中所示。对于黑色和灰色社区，需要将黑边集合及灰边集合与白边集合区分开。从社区的角度看，目的就是寻找形成社区的边缘描述符集的集合。

为解释聚集边缘描述符集形成社区这种特性，采用了连接密度的说法。令C表示节点集组成的社区，E(C)表示C中所有成员两者之间的边集。即假定一个含有n个节点的集，则该连通图的边的最大数量为n(n-1)/2。定义边密度如下：

(1)

实现社区构成方法需满足ρ(C)=D的条件。其中，D表示给定的入链(内部连接)密度，取值为0≤D≤1，所涉及节点的数目|C|尽可能地大。作为输入量，D的合理取值取决于从网络中提取的结构尺度；阈值密度更低的对应于更稀疏的社区，阈值密度更高的对应更紧密的社区。

采取贪心算法扩展社区，如果它们将ρ降低到最小限度，但仍保持在给定的阈值以上，新的节点将被吸收到社区中，并连带产生新的边缘描述符集。从数学角度看，这不是最佳优化方法，但它保留了社区的直观形成过程，展示了社会网络的社区结构在各个角度的扩张过程，这和文献[8]中边缘描述符集的渗流法相似，也可看作是文献[9][10]的变体。社区扩展算法描述如下：

输入：网络中已经检测到的所有边缘描述符集

算法：

① 从最大的未聚类的边缘描述符集开始，以此作为社区基础；

② 为将形成的社区找到使入链密度降低到最低限度的边缘描述符集；

③ 如果入链密度保持在用户提供的密度阈值以上，添加边缘描述符到将要形成的社区中；

④ 重复步骤②和步骤③直到没有边缘描述符集满足密度约束条件；

⑤ 重复步骤①直到没有边缘描述符集保持未聚类。

输出：社区的初始集。

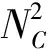
1.3 社区结构的网络尺度特性

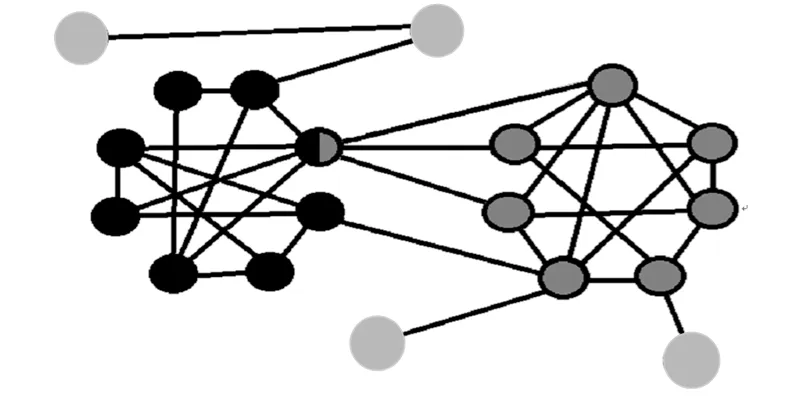
图3 社区网络节点聚类示意图

为最终实现网络中没有剩余的未聚类的节点，且社区个数为最少，还须挖掘出整个网络层面上的社区特性。这里采用常规启发式方法，保证了网络中的节点集有社区隶属关系。

对于图3中的网络，关键在于这些不确定属于任何社区的节点该如何处理。首先使用前面提到的方法形成社区的初始集合，强行要求所有节点至少属于一个社区。对于始终保持未聚类的节点，将其分配到与其连接最多的社区。如有必要，迭代此过程，直至没有未聚类点。从最大的社区开始作为集合中第一个元素，随后社区被成功地添加到该集合中，在已检测到的社区外建立一个保护层，该保护层和现有保护层有最低重叠比例。当多个社区被约束了最低比例，大社区的优先级将高于小社区。一直执行此过程，直到网络中每个节点至少属于一个社区。

2 实验结果与分析

采用人工合成网络和现实世界网络对模块化多尺度检测算法的性能进行测试。人工合成网络选用LFR基准测试，现实世界网络选用中学朋友圈网络[11-12]。使用标准社区作为检测社区的评价依据，采用精度、召回率、F分值来评定社区检测算法的有效性。几项评价指标由公式(2)到(4)定义。

(2)

(3)

(4)

当每个检测到的社区以最高的F分值和标准社区配对时，社区内节点代表每个集合的元素，精度和召回率是指平均的精度和召回率。利用这个度量评定算法的优势在于，精度直接反映了选择的边缘描述符集的质量，召回率反映了选择的社区组成和网络等级特性的质量。

为了测量在LFR基准测试和中学朋友圈网络中算法的性能，另外计算了两个社区标签集间的规范化互信息(NMI)的扩展概念[13-14]。受到文献[12]中用到的性能度量的启发，这些测试措施允许本算法和其他大量算法作比较。尽管NMI的扩展概念与所谓的标准NMI有稍微差异，但是为便于计算，在文中也称这个扩展版本为NMI。NMI分值为1，表示标签间有很好的关联；NMI分值为0，表示标签间没有关联。

2.1 LFR基准测试

设计这种测试的目的是构造内置社区结构的综合网络。LFR网络模型中的节点度不需要全都相同，社区也可为不同尺寸。在考虑边的权重和方向时，有很多常规的测试方法可供选择[15]，但是这里注重测试的扩展形式，这种形式允许节点同属多个社区，即重叠节点。设已知网络中重叠节点的总数记为On，重叠社区个数记为Om。

为便于将本算法和文献[12]中算法结果作比较，在实验中采用与之一样的参数。节点度和社区规模分别由幂律分布绘制，其中τ1=2,τ2=1，设每个节点的平均度kave=10，设一个节点的最大度kmax=50，剩余的参数根据测试而定。采用的社区规模为N∈{1000,5000}，社区规模在小区间s=(10,50)和大区间b=(20,100)之间浮动。社区内节点与其他社区间的少量连接记为混合参数μ。最后，为每组参数值随机生成了20个网络，计算其平均性能。

前4组实验中，设定重叠社区的最大个数为常数，Om=2。增加社区间边密度，参数μ从0.1以0.05的增量增加到0.3。On设定为网络中节点数的10%或50%，N和社区规模的参数值的所有可能组合都测试一遍。对于这组测试，考察了每组社区的精度、召回率、F分值和NMI的平均值。社区扩展的截止密度通过自我中心网平均密度进行(1-μ)倍增。

经测算，当社区的数量和规模增加时，算法的性能也在提高。同时，在低重叠的情况下，算法的F分值也随着混合参数值的增加而提高，这里的On等于节点总数的10%。这种情况可理解为，当增加μ时，社区内的边缘密度相对降低了。可以用一个更低的边缘密度阈值来合并连通图并发现社区，从而提高召回率。同时，由于On很小，社区始终保持分散状态，这时出链的增加对散乱连通图的产生无效。然而，对于高重叠的情况，发现增大混合参数的值将对召回率仅有微小的效果，但是却显著降低了精度。

测试的后4组中Om从2到8变化，N=5000，μ=0.3，On等于节点总数的10%。这组测试中算法的精度、召回率、F分值、NMI如图4和图5所示。结果表明，相较于其他算法，本算法的精度值更高。

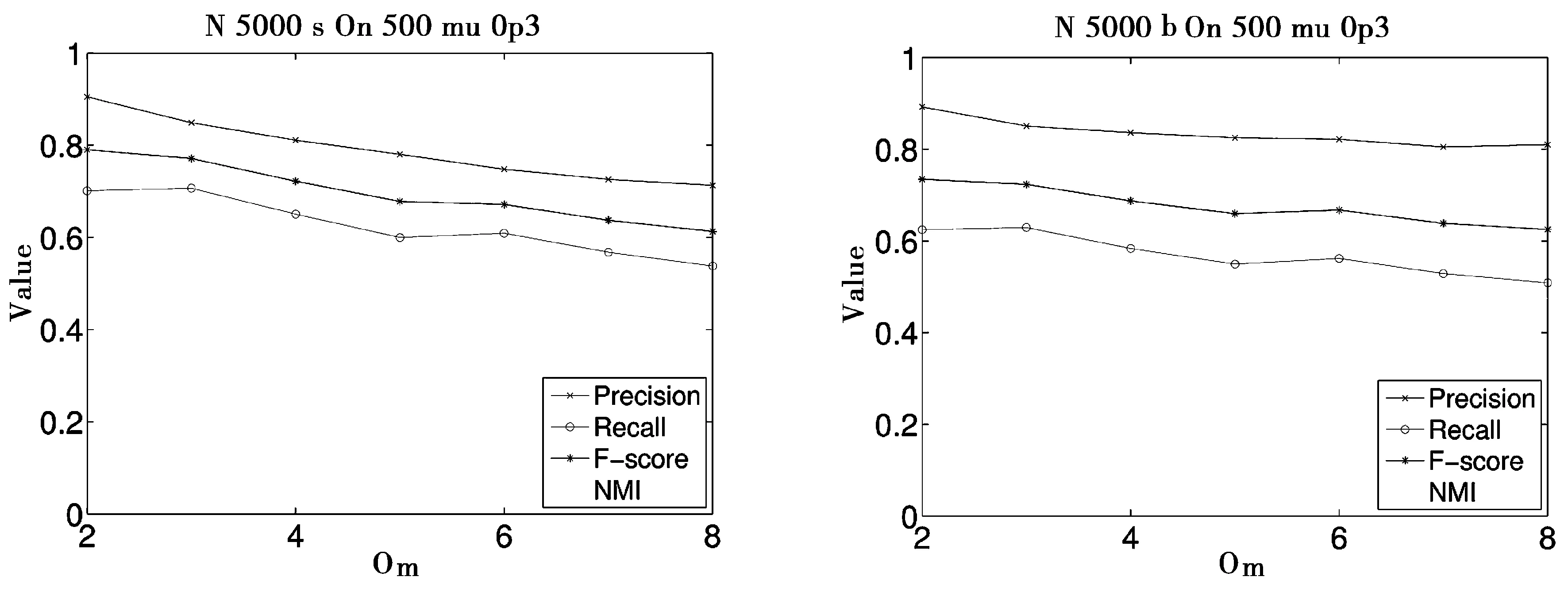
图4 使用小的社区规模范围时的算法性能 图5 使用大的社区规模范围时的算法性能

2.2 中学朋友圈网络

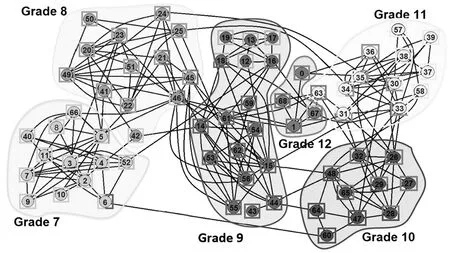
图6 中学朋友圈网络分组情况图

中学朋友圈网络的数据集是青少年到成人健康的国家纵向研究的一部分。这个现实世界网络经常被用在重叠社区检测算法评价中。该网络由中学生组成，学生间的连接指自发社交联系，网络的标准分区是学生所属的年级(假设分Grade7到Grade12，如图6)。尽管本来是6个社区，但是9年级的友谊连接显示，这个年级可以被分成两个不同子组，第一组由黑人学生组成，另一组由白人学生组成，图6中清楚地划分出学生的分组情况。

通过考察每个节点自我中心网的平均局部边密度，来估计期望的社区密度，并且把社区连接密度设为前者密度的3/4。对于中学朋友圈网络，经计算自我中心网的平均连接密度是67.0%，因此社区密度阈值设为50.3%。然后将社区形成后依然是未聚类的节点，安排它们属于与之连接最多的社区。本算法在该网络中的表现如表1所示。

表1 本算法在中学朋友圈网络中的表现

算法在紧密连接的几个年级中，精确地检测出了9年级的子划分，对朋友圈网络的检测结果也是合理的。由几项量化评价指标同样可以看出，算法准确性还是比较高的。

3 结语

利用社区结构的多尺度特征，设计了一种重叠社区检测算法。通过考察节点尺度、社区尺度以及网络尺度，分别量化每种尺度特征并结合在一起，建立了高度模块化的模型。可根据具体社区检测问题，对社区结构的数学模型作适配调整。LFR基准测试显示算法具有良好的综合性能。随着社区数量或者社会规模的增大，算法的性能也在提高。经现实世界网络验证，结果表明本算法可以较准确地检测重叠社区。