基于枚举法的应急物资储位优化研究——以我国新型冠状病毒肺炎疫情应急物资为例

刘倚玮，赵章荣 （北京物资学院 物流学院，北京101100）

2020 年新型冠状病毒肺炎突发时期，来自各地的救援物资源源不断的汇聚到武汉。然而，此次疫情防控尤其是在前期，面对大量的物资的聚集，应急物资调配混乱、不及时不准确的问题突出。其主要的原因就是此次疫情期间需要的应急物资流量相对于平常增长非常大，不易于进行管理，而且对应急物资的储备没有一个系统的规划，不利于疫情的及时防控。这些也是社会各界关注的焦点，疫情防控监督的重点。习近平总书记在统筹推进新冠肺炎疫情防控和经济社会发展工作部署会议上强调[1]：“要加强医用物资和生活必需品应急保供。打疫情防控阻击战，实际上也是打后勤保障战”。

1 应急物资储备理论研究

应急物资储备仓库是我国应急物资储备的主体，对应急物资储备的评价应以仓库为主体表现特征。应急物资的储备问题已经受到许多学者的关注，大部分学者对其研究都集中在应急物资储备中心选址的问题上，文献[2]中通过建立一个应急物资储备库和需求点之间需求量与运输距离乘积之和最小为优化目标的多目标选址优化模型，然后设计算法进行求解，提高了应急物资储备仓库选址的效率。文献[3]中构建了基于层次分析法的应急物流选址优化模型和应急物资配送路径优化模型，并结合实际案例进行了论证。文献[4]中奥地利学者考虑到灾难过后必须建立一个带有中间仓库的供应系统，以向受影响的人们提供救济品，从而提出了一种精确求解方法和一种“数学启发式”技术，该技术建立在具有启发式生成约束池的MILP 公式上，解决了多基地、多行程的团队定向问题。文献[5]中提出一个称为“预防可靠性”的新概念对仓库位置的可靠性问题进行了建模，最后应用到了德黑兰救济领域仓库的实际案例中。还有的研究人员对国内外的应急储备体系进行了优化，文献[6]中对协调优化应急物资储备体系的概念和因素进行分析，建立了基于协调优化的区域应急物资储备体系。文献[7]中采用需求理论、库存理论和多目标决策等理论分析了物资需求情况，奠定了建立“情景—应对”型应急物资储备体系的基础。此外，还有文献从应急物资的调度方面进行研究，文献[8]中提出了基于混沌粒子群算法的应急物资调度模型，然后对设计算法进行求解，其结果有效解决了物资调度问题。文献[9]中在阐述人道主义物理概念和应急物资类别的基础上对应急物资调度研究进行了综述和思考。

文献[10]以立体仓储系统为研究对象，对目前较流行的遗传算法和枚举法货位优化算法进行比较与分析，仿真及优化结果表明，枚举法的优化结果优于遗传算法，因此本文将采用枚举法来解决应急物资储备库的储位优化问题。

通过上述的文献研究发现，现在学术界对应急物资储备的研究还不够深入，并没有形成一定的体系，还可以看出我国对应急物资储位优化方案方面的学术研究相对较少，缺少具有实践意义的方法，与实际的应急物资分配工作相脱节。因此，本文的研究结果可以优化应急物资储备仓库中应急物资的储位摆放，具有很强的实际意义。

2 新冠肺炎疫情中的应急物资储备现状

当疫情突发时，需要大量的医用应急物资，而且物资的种类多种多样。应急物资储备库中主要的医用应急防护物资有：医用外科口罩、防护服、护目镜、速干手消毒剂、N95 口罩、医用手套、测温枪、一次性鞋套、84 消毒液、医用酒精等。为满足疫区的紧急需要，这些医用防控物资统一进行筹措，然后集中运送到应急物资储备库，再由相关志愿者负责仓库运维和调运分发。

我国应急物资储备库目前存在的主要问题是除了代储点少和分布不合理，储备库的硬件设施还不够完善，仓储管理方面也存在很大的问题，仓储管理中最重要的问题之一就是储位规划的优化问题。应急储备中心要求在时间短、成本低、效率高进行物资配送。

应急储备库内医用防护物资种类繁多，当需要配送应急物资时，都是依靠志愿者进行拣选和作业，物资的摆放位置大多是随意进行摆放的，哪里有空缺储位就摆放在哪里，并不能多方面考虑各单位的多种需求。应急物资的需求量基本上都很大，从而导致供货不足，响应不及时和应急物资丢失等问题。

我国初期是新冠状肺炎疫情最严重的国家。大部分应急物资储备库缺少必要的仓储设备和设施，都是由志愿者人工进行搬运，大大降低了应急物资装卸和搬运的响应速度，不利于对疫情进行及时的防控。对此，本文将对应急物资储备物流系统建立数学模型，基于枚举法进行多变量储位优化研究。应急物资合理的储位摆放，不仅可以降低成本，而且还能够保证提供应急物资的时效性，它直接影响应急保障的效率和效果[11]。

3 模型建立

3.1 模型条件假设

应急物资具有自己独特的特点，因此模型的构建将不同于一般的物资假设，即提出一系列假设的前提，使研究的目的更加明确。

本应急物资储备系统的假设条件为：

（1） 该应急物资储备系统属于单元货格式存储形式，现有堆垛机和货架。

（2） 货架为矩形，总共有i层，j列，长度是L，高度是H。

（3） 包含众多应急物资，货架上全部尺寸相同，且任何储位都随意摆放。

（4） 系统中对不同应急物资的需求相对清楚，且不会改变，不同物资没有关联。

（5） 堆垛机可以在两个方向，即水平和垂直方向上同时进行运动，本文假设水平和垂直方向上的最大速度分别为Vx和Vy。

（6） 应急物资为通用物资。

3.2 模型建立

对应急物资储备库进行优化，主要是解决多目标函数的优化问题，因此，用权重系数法把多目标问题转为单目标问题是解决储位优化问题的一种方法，本文仅考虑应急物资的出库率和物资重量这两个关键的要素在储位分配优化上产生的影响。

（1） 应急物资储备库基本参数（如表1 所示）

表1 应急物资储备库基本参数

为了减小篇幅，货架取5 层10 列。

（2） 目标函数

基于堆垛起重机运行时间最少的原则，所以，堆垛起重机的运行时间和物资的出库率相乘之和最小时，可以得到第一个优化目标条件：

式中：tij为堆垛起重机运行到第i列第j层储位时运行时间；fij为第i列第j层储位对应的出库频率。

基于上轻下重的原则，设地面底层为第1 层，离出库口最近的列为第1 列，当每个物资的所在层与其质量的乘积之和最小时，得到第二个优化目标条件：

式中：Wij为第i列第j层储位对应的物资重量。

通过上述这些优化函数可以看出，在进行储位优化时，既要考虑货架是否稳定，也要考虑应急物资存取效率如何，这是把多个目标组合起来进行优化的问题。

在解决多目标函数问题转化成单目标函数问题时，可以运用权重系数法。假设，a和b为两个函数的权重系数，然后分别对两个系数a和b进行赋值，即令a+b=1，得所求的单目标函数公式为：

以5 层10 列的货架为例，计算堆垛起重机运行到第i列第j层储位时运行时间，公式为：

通过上述式子可以得出堆垛起重机从进出库站台到所有储位的单层运行时间tij（s）。

4 应急物资储位优化仿真实现

假定应急物资储备库内部存放10 类应急物资（医用外科口罩、防护服、护目镜、速干手消毒剂、N95 口罩、医用手套、测温枪、一次性鞋套、84 消毒液、医用酒精） 依次用数字1-10 表示，有关应急物资出库率以及重量数据如表2 所示。

表2 不同种类应急物资出库率和重量对应表

假设所有储位的使用率是80%，参考实际系统以往的数据，明确不同类型应急物资的预估最高存储量，把全部应急物资随意放置在库中，未放置应急物资的则是空储位。储位分配优化以前具体分布情况如表3 所示。表3 中数字主要代表不同应急物资的编号，数字0 代表储位没有放置物资。

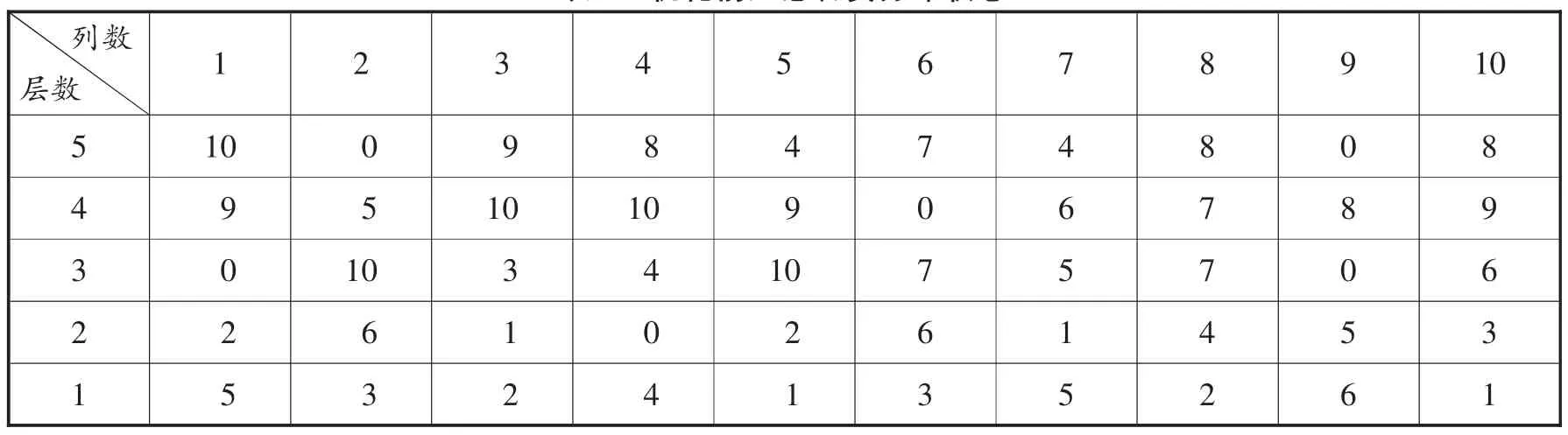
表3 优化前应急物资分布状态

4.1 算例实现

应用在应急物资储备库储位优化上的主要思路是对储位交换的条件进行判断，首先任意选取货架上第i列第j层应急物资，假设已知其出库频率为fij，其对应的重量为Wij，利用该货物与第m列第n层应急物资进行比较，同样已知第m列第n层应急物资对应的周转频率为fmn，重量为Wij。计算两个储位对应应急物资的目标函数值的和P1：

然后再把货架上第i列第j层应急物资与第m列第n层应急物资进行交换，并通过求和计算P2值得到式（6）：

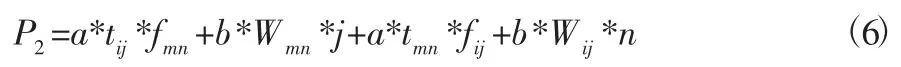
图1 50 次迭代搜索过程

把P1的值和P2的值进行比较，如果P1的值大于P2的值，则第i列第j层应急物资与第m列第n层应急物资进行交换；反之，不进行交换。通过逐一比较，从而获得一个比较合理的储位分配方案。

4.2 利用Matlab 求解

将原始数据代入Matlab 软件中进行仿真计算，求解初始数据，为得到更接近最优解的数据，对其迭代50 次，仿真结果如图1 所示。

每次迭代，都会产生不同的结果，影响储位的分布和拣选的效率。根据数据和以往经验的判断，当迭代的次数达到一定时，所得结果可以当作是最优解。

优化前的总目标函数的目标函数值为15 080，优化后的总目标函数的目标函数值为10 920。

进行储位分配优化后，优化后的仓库应急物资分布如表4 所示。

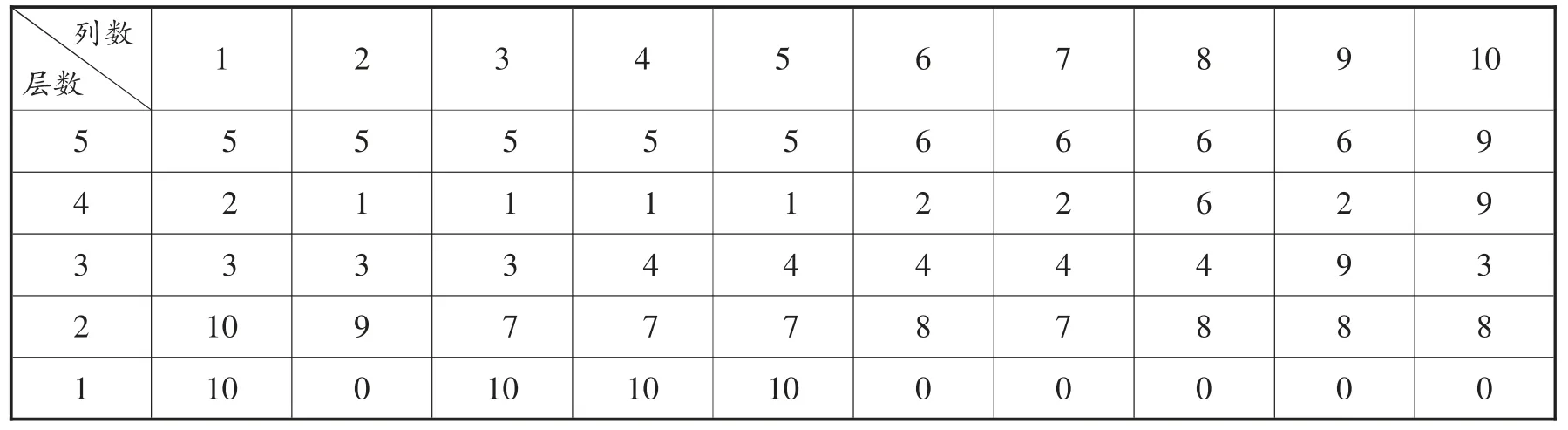
表4 优化后应急物资分布

从优化结果可以看出，基于考虑应急物资重量和使用率的优化模型进行优化，较重的应急物资应该放置到货架的底部，较轻的应急物资应尽量放置到货架的上部，应急物资使用率高的被分配到了离出库口近的地方，使用率低的被分配到了离出货口远的地方，从而保证货架的稳定性。

4.3 结果分析

通过对相同目标函数的不同方法计算，表明不同目标函数都可以得到全面的优化。在进行优化之后，使用率高的应急物资被储存到接近出货口的储位，重量大的应急物资则普遍存放于货架底层储位，提高了拣货的效率。经过对比，得出结论如表5所示。

表5 优化前后目标函数值对比表

5 结论和展望

新型冠状病毒肺炎疫情形势十分严峻，面对此类重大突发公共卫生事件，应急物资的及时供应显得十分的重要。防疫物资是疫情防控工作的生命线，也是保障抗疫战士生命健康的关键[12]。本文以立体仓库为研究对象，建立了储位优化的模型，并利用枚举法进行了求解，通过仿真实验验证了模型的可行性和合理性。本文研究以期能够加快应急物资出库响应速度，降低库存成本，为疫情防护工作做出贡献。本文在研究应急物资储位摆放时，并没有考虑物资本身具有的易燃性和腐蚀性等特点，后续可结合实际情况进行研究和改进。