制造商再制造技术视角下闭环供应链定价和协调策略研究

刘 旭 （江苏大学 管理学院，江苏 镇江212013）

0 引 言

近年来，环境保护和可持续发展逐渐进入人们的视角，很多企业也开始利用废旧产品进行产品的再制造。施乐（Xerox）通过回收废旧的打印机和复印机用于产品的再制造过程，每年可为企业节约两亿美元的制造成本；惠普的计算机和外围设备通过利用直接渠道进行回收；Canon 将直接回收渠道用于回收打印墨盒；伊思曼—柯达公司通过和零售商合作来回收一次性照相机，并且利用回收的纸板制作胶片盒，在一定程度上为公司节约了制造成本[1]。我国在废旧品的回收再制造上面起步较晚，同时企业在再制造时对于废旧品也存在利用率低的问题，导致从事废旧品再制造的企业不能很好地利用废旧品的价值，这和企业再制造的技术有直接联系。所以，在回收废旧品并利用其进行再制造时，考虑企业再制造技术这一因素尤为重要。

国内外有关闭环供应链的研究较为丰富。主要集中在以下几个方面：（1） 考虑质量不稳定性方面的研究：刘家国[2]基于不同的产品质量，分析了不同策略下的闭环供应链定价问题，研究发现分散决策下的销售价和回收价较高，利润则较低，并提出了基于差额利润的共享机制以提高链条效率。邹清明等[3]研究产品设计可回收利用部件的不同比例以及回收产品质量差异引起的再制造成本随机变化时闭环供应链的定价与协调；Huang M 等[4]结合工程机械再制造领域的一个实际案例，在博弈论的框架下，考虑了闭环供应链的多维逆向渠道并构建了模型，基于不确定性的废旧产品质量对回收价和再制造成本的影响，分析了动态定价和回收策略。（2） 闭环供应链双渠道定价协调研究方面：Wang K 等[5]针对再制造服装产品如何选择渠道结构的问题进行了研究。政府为再制造厂商提供补贴，以激励再制造厂商。结果发现：无论再制造厂商如何选择渠道，补贴都能够对再制造活动起积极作用。此时，随着消费者对再制造产品的认可度提高，再制造厂商和制造商的竞争力也会进一步提高。然而，从社会福利和环境保护的角度来看，再制造企业的最佳渠道选择可能效率低下。Shu-San 等[6]研究了单一渠道销售和混合渠道销售的闭环供应链定价决策问题，在单一渠道中，新产品和再制品一起销售；在混合渠道中，新产品通过常规的销售方式进行销售，再制品通过厂家直销的方式销售，结果发现混合销售渠道的最优定价决策优于单一销售渠道，且供应链的整体效益也高于单一销售渠道。（3） 渠道冲突环境研究方面：Nikunja 等[7]基于闭环供应链渠道冲突背景下研究回收质量对于回收价格和回收数量的影响，并设计出一种均衡定价策略来解决渠道冲突的问题，闭环供应链由此可以得到协调；彭志强等[8]基于两种不同的政府补贴模式，分别建立了不同的闭环供应链模型，并提出一种数量折扣—收益共享契约来解决分散模式下出现的双重边际化问题；Padhi S 等[9]研究政府激励对三级再制造系统经营决策的影响，结果表明，在完全竞争条件下，随着政府激励的增加，回报率和渠道利润也会随之增加。（4） 随机需求研究方面：He[10]构建了分散决策和集中决策两种决策模型，考虑了不确定性需求对闭环供应链的最优决策以及效益的影响，并提出协调策略来提高供应链的效率；Gao 和Wang 等[11]构建双渠道回收下需求不确定性的博弈模型，分析比较分散模式下三种不同回收情形的最优决策，结果发现随着需求不确定的增加，零售价格和利润均下降，但是最优回收价格和最优收购价格却不受需求的影响。

这些文献主要都是研究闭环供应链的定价策略问题，但是很少从制造商再制造技术这一视角来研究闭环供应链成员最优定价策略和经济效益。本文将考虑制造商回收、零售商回收和第三方回收三种模式，基于此分别构建集中决策和分散决策博弈模型，并对比在这几种情形下的最优定价策略和供应链效益，探讨再制造技术对它们的影响。然后通过简单的算例分析更加直观地看出再制造技术对于闭环供应链的影响，最后提出一种差额利润共享契约来提高供应链的效率。

1 问题描述

本文的研究对象是制造商、零售商和回收商构成的闭环供应链，制造商回收产品，可以直接回收，也可以通过零售商或第三方间接回收。假设回收的废旧品质量没有差异，新产品和再制造品性能完全相同，制造商以相同的价格将新产品和再制品批发给零售商，零售商然后以相同的零售价格销售给顾客。

参数设定：

p为单位产品销售价格。

ω 为单位产品批发价格。

t为单位废旧产品的技术研发投入。

r为再制品利用废旧品的比重，r∈（0,1），r与t之间是正比关系，单位产品的技术研发投入越大，则对于废旧品的利用比重r越大，即r=k1t；k1为利用比重r对于单位产品的技术研发投入t的敏感系数，为一个定值，可根据行业特征对其进行界定。

ch为环保成本，废旧品未利用部分会对环境造成一定危害，需要对其处理所产生的费用。ch=F-k2t，F是在制造商未对废旧品进行技术投入时所需要处理危害品的成本，且为定值，V是单位废旧品总价值，这里假设每个废旧品的总价值相同，且V＞F，也就是说，废旧品的剩余价值大于环保成本，否则制造商拒绝回收。k2是环保成本ch对于技术投入费用t的敏感系数，为一个定值，可根据行业特征对其进行界定。

cn为新产品的制造成本。

cr为再制品的制造成本，由两个部分构成：一部分是利用废旧品的残余价值，一部分是购买新产品材料的成本，即cr=rV+（1-r）Cn。

c为产品单位制造成本，c=（1-ρ）cn+ρcr，ρ 为回收商的产品回收率。

H为回收渠道固定成本，废旧品的回收率与其投入成本正相关[12]。h为规模系数，则可得回收渠道固定成本为H=hρ2。

A为回收商付给消费者的单位回收价格。

B为制造商付给回收商的单位回收价格，且A＜B。

Vs为未利用的废旧品价值，由于技术限制，废旧品部分材料不能利用，但是可以经过简单的处理转售给别的制造商，从而获取利益，Vs=（ 1-r） V。

D为市场需求，D=a-bp，a为市场总需求，b为市场需求对销售价格的敏感系数。

2 模型的构建和求解

2.1 集中式决策模型（模型C）

在集中决策模式下，闭环供应链中的每个节点企业作为一个整体，制造商是唯一的决策者，决策变量为：零售价p、回收率ρ。

此时整条闭环供应链的利润：

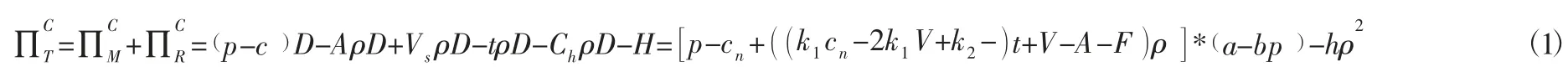
对式（1） 分别求p和ρ 的一阶偏导数，为方便计算，令X=k1cn-2k1V+k2-1，联立可得最优零售价格和回收率：

此时整个闭环供应链的利润为：

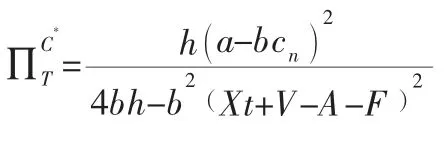
2.2 制造商回收模型（模型M）

在制造商回收模型中，制造商首先决定批发价格ω 和回收率ρ，然后零售商根据制造商的决定确定自己的销售价格p。制造商和零售商的利润为：

采用逆向归纳法求出模型的最优解为：

2.3 零售商回收模型（模型R）

零售商作为回收商时，首先由制造商决定批发价格ω；其次零售商决定销售价格p以及回收率ρ。此时制造商和零售商的利润为：

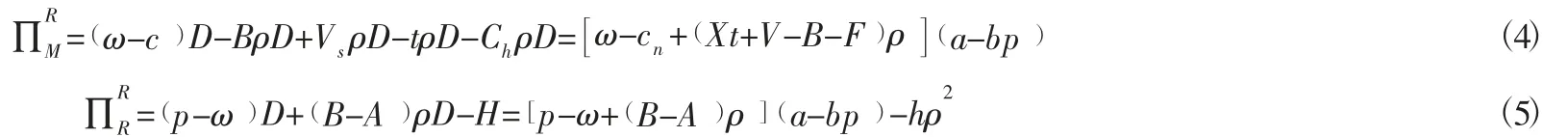
同上利用逆向归纳法求得模型最优解为：

2.4 制造商委托第三方回收模型（模型3P）

制造商首先决定批发价格ω；零售商根据制造商的决策来确定销售价格p；最后再由第三方回收商根据批发价格和零售价格来确定回收率ρ。

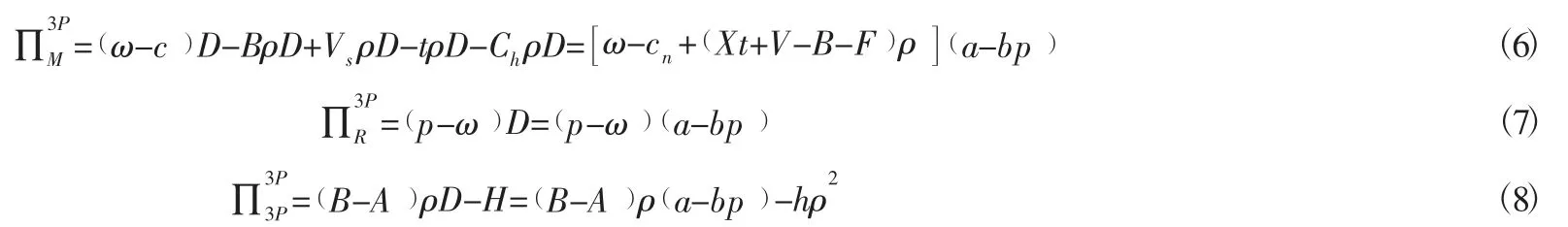
同样利用逆向归纳法解得模型最优解为：

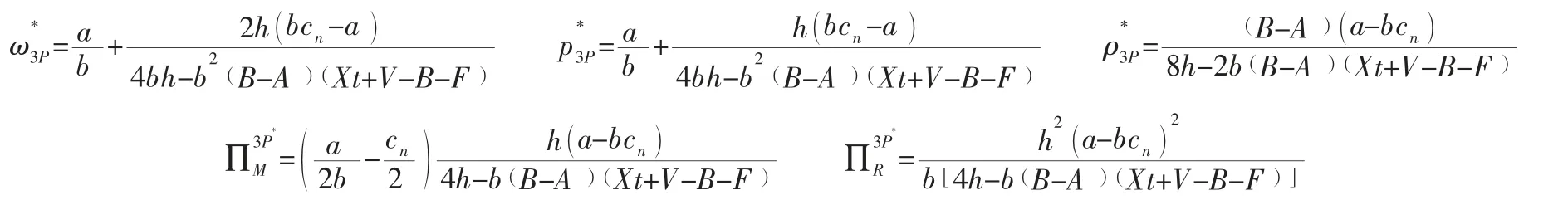
3 四种情况下最优解比较分析

本节将对比分析四种不同回收情形下的最优解，并且探讨单位废旧产品技术投入对于系统最优解以及供应链各成员效益的影响。

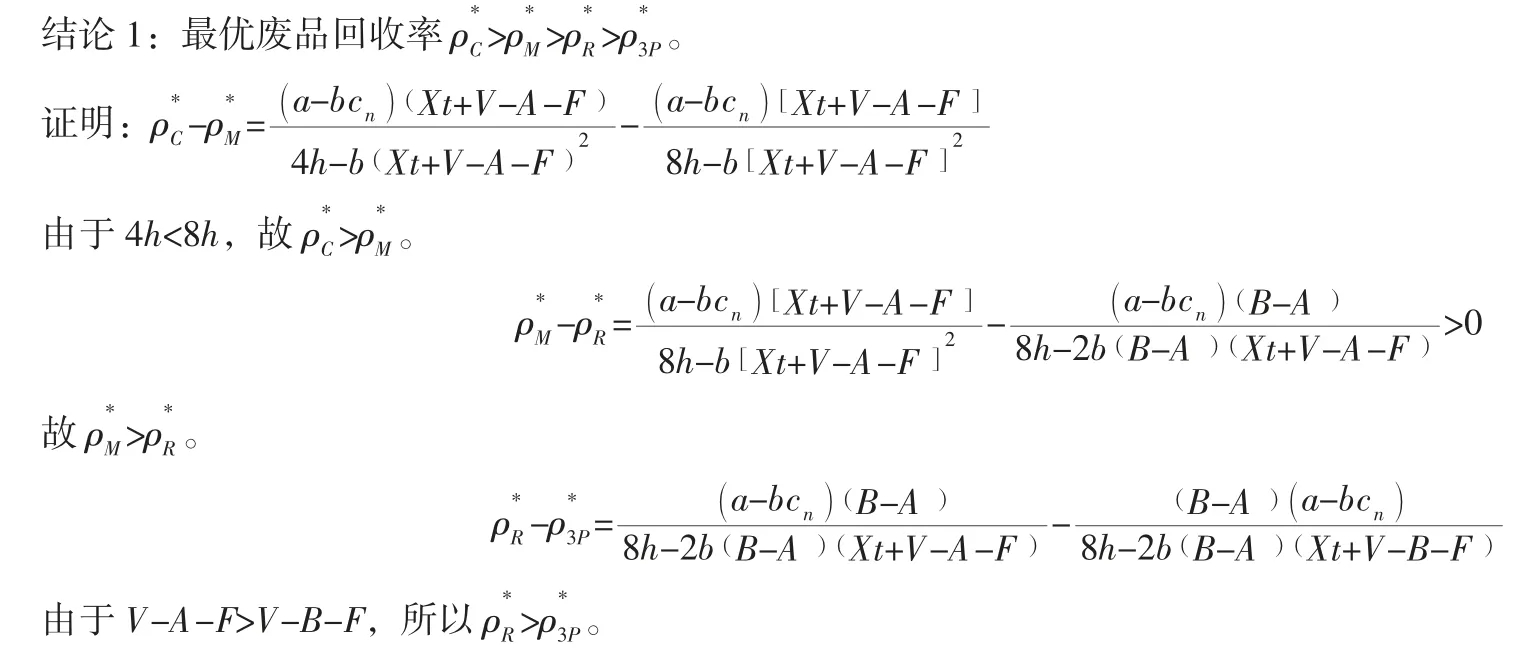
即得结论1。

一般认为回收人员的回收率与其距离消费者市场的距离呈正向关系[13]。但是，在考虑企业再制造技术因素时，制造商的回收率最高，第三方回收商的回收率最低。随着回收率的提高，制造商在分散模式的三种情形下获得更多的效益，此时零售商和第三方回收商不愿投入过多的精力去回收产品，导致其回收数量较少，从而回收率也较低。

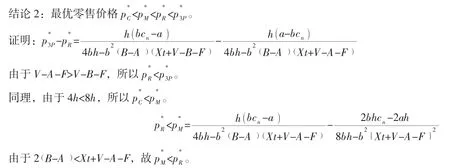
即得结论2。

由结论1 和结论2 可知，回收率在分散决策时较高，而零售价格在集中决策时较高，说明分散模式降低了供应链的效率，这就需要一个相应的协调机制来提高供应链的效率以及提高消费者的效用。

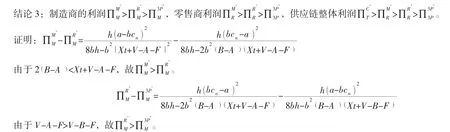
其余两种情形同理可由简单的代数运算来证明。

结论3：在分散决策下的三种回收情形中，制造商和零售商以及供应链的整体效益在制造商回收时最大，说明制造商作为回收商时，可以为系统带来更多的效益。

结论4：在闭环供应链中，无论采取何种回收方式，企业对废旧产品的技术投入加大都将会提高废旧品的回收率，并降低产品的零售价格和批发价格。

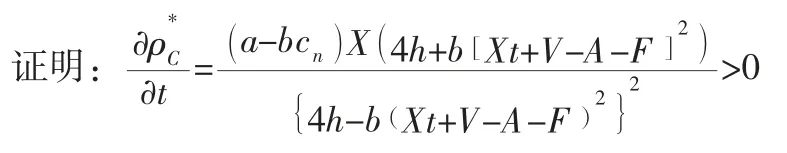
故回收率随着t的增大而增大。

其他两种情形同理可证。

结论5：当企业再制造技术提高时即对废旧产品的技术投入提高时，无论是哪种回收情形，闭环供应链上各节点企业的效益以及整体效益都会增加。

证明：

其他三种情形同理可得证明。

结论4 和结论5 表明，随着企业增加对单位废旧产品技术的资金投入，废旧品的回收率将会增加，相应的企业对废旧品的利用率也会增加，获得了更多的残值效益，导致了企业生产的单位产品成本减少，批发价格也降低，同时顾客获得了更多的产品效用。虽然价格降低了，但是市场需求却随着销售价格的降低而提高，这就导致闭环供应链上各组成成分的利润不但没有降低，反而提高了。企业因此也有更大的动力来加大对废旧产品利用技术的投入，以此来获得更大的经济效益。

4 数值模拟

为了更好地理解制造企业再制造技术对闭环供应链最优决策的影响，通过数值模拟的方式更为直观地来对比几种不同的回收情形。首先计算出再制造技术投入为定值时系统中各决策变量和各成员的利润，并考察不同回收模式下的各参数随技术投入变化而变化的情况，取初始参数，b=10、cn=80、k1=0.02、F=20、V=40、h=2 000、A=10、B=15、t=5、a=1 000。结果如表1 和表2 所示。

表1 技术投入为定值时四种情形下最优解

表2 三种回收模式下再制造技术对闭环供应链的影响

从表1 中可以看出：当企业的再制造水平为一定值时即企业对废旧产品的投入为定值时，集中模式下的各成员利润最高，并且产品的零售价格最低、废旧品的回收率最高。在分散模式决策的三种情形下，批发价格和零售价格在制造商回收时最低，回收率在制造商回收时最高，在第三方回收时最低；在利润方面，制造商回收时可以带来更高的利润，渠道中的各个成员利润都比在另外两种回收情形下的要高。

从表2 中可以看出：随着再制造技术的不断提高即技术投入的不断增加，不管在哪种回收情形下，废旧产品的回收率都是提高的；产品的批发价格ω 和零售价格p都降低，这是因为虽然技术投入费用增加，但随着技术投入的增加，企业对于废旧品利用率也会提高，即可以利用更多的废旧品残值并降低单位环保成本，从而抵消了单位废旧产品的技术研发投入，进而为企业带来更多的经济效益，所以制造成本降低，产品的批发价格和零售价格也随之降低；闭环供应链的整体效益以及各成员效益都会增加。虽然零售价格和批发价格降低，但是需求的扩大不仅弥补了因价格降低而减少的利润，而且还带来了更多的效益，所以利润是提高的。因此，企业在发展时应当提高对废旧产品的单位研发投入对于整个闭环供应链以及各组成成员都是有益的。

5 协调策略

在分散决策下，闭环供应链上每个节点企业以自身利益最大化为目标，这不仅降低了闭环供应链的整体效益以及各成员的效益，而且还降低了消费者的效用。面对这种情况，供应链上的制造商、零售商和回收商就有了合作的动力，他们的目标是追求集中决策和分散决策的差额利润。

在三种不同的回收模式下，制造商作为回收商时，闭环供应链各组成成员的效益以及整体效益都优于其他两种回收模式下的效益。因此，这里的差额利润是链条的整体利润分别在集中决策和制造商作为回收商之间的差额。

在此基础上，本文设计了一个差额利润分享契约来提高分散模式下供应链的总利润以及各成员的利润。假设差额利润分享比例为λ，即制造商保留λ 的差额利润，零售商分享到1-λ 的差额利润。

通过这个契约，制造商和零售商的效益都得到增加，并且增加的利润和差额利润与分享系数λ 直接相关，同时λ 的大小也反映了制造商在这一过程中的强势程度或者是付出的努力程度。

6 结束语

本文引入制造商再制造这一因素，分析了闭环供应链集中决策以及分散决策中三种不同的回收模式下产品的定价决策以及协调问题。结果表明，分散决策的效率较低；在分散模式下制造商作为回收商时系统达到最优；相反，在第三方作为回收商时最低。随着再制造技术的不断改善即技术投入不断增加，同时废旧品的利用率也不断提高，从而产品的制造成本降低，零售价格及批发价格也随之降低，销售数量得到提高，供应链上各成员效益及整体效益也随之增加。因此，制造商加大技术投入时将有利于其自身和闭环供应链整体。企业在发展时，应注重这方面资金的投入，引进技术人才，注重与高校进行技术学术交流，通过这些措施来支持技术创新，从而不断提高对废旧品的利用率。这样不仅可以获得更多经济效益，而且也为环境保护做出了贡献。本文还提出了差额利润协调策略来提高供应链的效率，在这一过程中引入了利润分享系数，它在一定程度上说明了制造商在这一过程中的强势程度或者付出的努力程度。

本文还有很多研究上的不足，单位废旧产品技术投入对利用比重以及环保成本的影响只考虑了简单的线性关系，在现实中它们的关系并没有那么简单。此外，还有众多影响闭环供应链运作结果的因素，如消费者环保意识，所以在以后的研究中将考虑单位废旧产品技术投入与利用比重以及环保成本之间更为复杂的非线性关系，并结合消费者环保意识这一因素来研究闭环供应链，从而获得更切合实际的结论。