随机风况下风力机翼型结冰对气动特性的影响研究*

（华北电力大学 电站能量传递转化与系统教育部重点实验室）

0 引言

风力机的工作环境复杂。例如，高原、寒冷地区以及山脊、山顶处的风资源通常较为丰富，具有很好的开发价值。然而这些地方海拔高、温度低、湿度大。工作在这些地区的风力机很容易遇到含有过冷液态水滴的空气或是雨雪天气，最终致使叶片出现覆冰现象。覆冰会改变叶片的几何形状，可能会降低叶片的气动性能，导致风力机组出力下降。其次，覆冰会增加叶片的质量，改变叶片的载荷分布，对机组的安全运行造成严重危害甚至出现运营事故[1]。因此，研究风力机结冰问题对寒冷、潮湿地区的风力机设计具有重要的意义。

结冰过程与叶片的迎风面积，以及空气温度、风速、空气中水含量和液滴直径有关，涉及到多相流与传热，过程复杂。实验是研究风力机叶片结冰问题的直接手段。结冰的实验研究通常采用自然环境下的外场实验或者特殊的冰风洞实验。Bose对某小型风力机在自然环境下的结冰过程进行了研究，获得了冰型轮廓和质量，并分析了其对风力机性能的影响[2]。Jasinski等采用低温风洞研究了结冰对S908翼型段气动性能的影响，发现不同的冰型对风力机的功率的影响有明显不同[3]。Hochart等人采用风洞实验研究了气象条件对风力机叶片结冰的影响，同时也研究了结冰对风力机的气动性能的影响[4]。国内的结冰风洞较少，仅有空气动力研究中心、东北农业大学、南航等几家单位建设有结冰风洞[5-6]，因此，相关的实验研究很少。东北农业大学的李岩教授团队利用冬季的自然条件，采用开口式风洞，开展了垂直轴风力机[7]与旋转叶片结冰的风洞实验[8]。

相比受制于风洞条件的试验研究，翼型和叶片结冰的数值模拟方法应用更为广泛。从上世纪50年代开始，国外研究者采用数值模拟方法对风力机翼型结冰问题进行了研究。Messinger[9]将结冰表面的传热过程假定为准定常过程，基于能量守恒，建立了计算结冰成长率的Messinger模型。该模型在飞机机翼的结冰研究中得到了广泛使用。MacArthur[10]建立了计算二维翼型的数值方法。他将模拟过程分为流场求解、水滴运动轨迹求解和结冰热力学模型求解三个步骤，在三个步骤之间进行迭代求解。这一思路将流场计算、水滴运动和传热进行了解耦，简化了求解过程，被当前的结冰模拟软件和程序所广泛使用，例如NASA的LEWICE程序。Kwon和Sankar将上述方法扩展到了三维，并在计算中考虑了三维真实冰型[11]。Homola和Nicklasson[12]等利用CFD方法模拟了NREL 5MW风力机叶片表面的结冰过程。Alberts的研究发现湿度大、温度低于零摄氏度时，风力机叶片结冰的概率会增大[13]。我国研究人员在翼型结冰的数值模拟研究也取得了很多成果。朱程香等人和胡良权等人采用RANS模拟分别研究了NACA63618翼型与S809翼型表面的结冰情况。易贤和王开春等针对过冷水滴在风力机叶片表面撞击并结冰的现象，建立了适用于风力机叶片结冰过程中水滴收集率计算的三维数值计算方法，并开发了计算程序[14]。蒋维等人利用商用CFD软件对风力机叶片和风轮的结冰过程进行了数值模拟[15-16]。

以上的风力机叶片翼型结冰的相关研究中，并没有考虑风力机工作的来流条件具有一定的随机性。其来流风速和风向等参数均是服从一定概率分布的随机变量，如高斯分布和Weibull分布。由于结冰的冰型与来流条件直接相关，结冰后叶片或翼型的几何表面的变化具有一定的不确定性，进而对其气动特性的影响也具有不确定性。在风力机气动性能处于敏感区间时，例如在翼型失速点附近，结冰对风力机气动性能影响会有显著的变化。

因此，本文对考虑来流风况随机变化情况下风力机翼型的结冰过程进行模拟，并研究这种不确定性在流场中的传播，以及翼型气动特性的响应变化。由于传统的采样法，如蒙特卡洛法，需要大量的样本，计算量大，效率低。因此本文采用基于谱展开的多项式混沌法。根据与CFD模拟耦合方式的不同，多项式混沌方法分为嵌入式和非嵌入式方法[17]。王晓东等采用概率配点法(NIPRCM，Non-intrusiveProbabilistic Collocation method)构造多项式混沌，研究了在工作条件含有不确定性参数时翼型和转子气动特性的变化，以及不确定性扰动在流场中的传播[18-19]。研究结果显示该方法可以在保证计算精度一定的情况下大大减少确定性计算点的数量，从而提高了计算效率。

本文首先对确定性来流参数下翼型结冰进行了模拟，获得确定性参数下的冰型和翼型气动参数的变化。在此基础上，采用概率配点法结合CFD方法模拟了来流风速和攻角发生随机波动时，翼型结冰冰型的变化和统计特性，及翼型气动特性对此不确定性参数的响应特性。

1 翼型结冰过程的确定性CFD模拟

本文研究的模型为NREL S825翼型，其型线如图1所示，图中x，y为型线坐标，c为弦长，在本文研究中，弦长设置为1m。

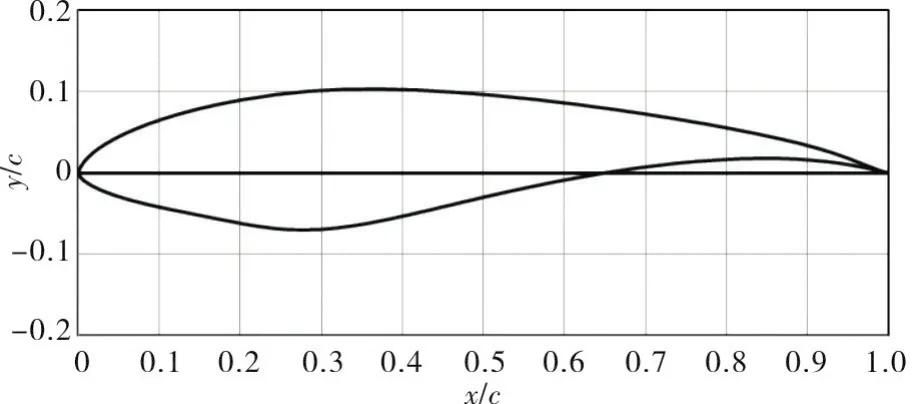
图1 S825翼型几何型线Fig.1 Geometry profile of S825 airfoil

1.1 结冰模拟计算设置

采用FENSAP求解器求解定常雷诺平均N-S方程，离散方法采用中心差分格式，湍流模型为Spalart-Allmaras方程模型。给定来流风速为28.6m/s，大气压力，气温为-10.3℃，给定空气中液态水含量（LWC）为7.5×10-4kg/m3，水滴直径20μm，密度为1 000kg/m3。翼型表面所结冰的温度为-5℃，结冰时间设为420s。给定翼型壁面为绝热无滑移条件。

1.2 不同攻角下冰型

图2给出了420s后，0°～12°攻角下翼型表面结冰后的廓线，图中AoA表示攻角，clean airfoil表示没有结冰的翼型，iced表示结冰的翼型，0deg表示0度攻角，其他数字以此类推。从图2可看出在其他各个参数相同的条件下，结冰现象主要出现在翼型前缘处，并且结冰形状多带有棱角状，因此可以断定所结冰为明冰。

图2 不同攻角下翼型结冰冰型Fig.2 Icing profiles of airfoil under different angles of attack

随攻角的不同，引起翼型表面结冰的形状、位置也有所不同。当攻角为0°时，水滴撞击到翼型后，没有被立刻冻结，由于翼型前缘的“阻挡”，水滴会分别沿着翼型上、下表面继续向后流动，因此翼型吸力面和压力面都有冰层的分布，形状接近对称。当攻角为2°时，没有被冻结的水滴沿着翼型吸力面继续向后流动，结冰分布主要集中在翼型上表面。但是随着攻角的继续增大，翼型前缘与压力面成为水滴主要撞击的位置，冰层的位置向前缘和压力面移动。由于压力面前缘附近存在逆压梯度，没有冻结的水滴无法沿着压力面继续流动，因此翼型压力面前缘附近出现了较厚的冰层。

2 结冰对翼型气动力的影响

2.1 计算设置

结冰模拟提供了结冰后翼型的几何。为了研究结冰对翼型气动力的影响，采用CFD对结冰后翼型的绕流场进行模拟。NUMECA的AutoGrid5模块生成结构化网格，每个攻角的网格均采用相同的拓扑结构，网格总数均为14万左右。计算采用FINETM/TURBO求解器求解定常雷诺平均N-S方程，采用二阶中心差分格式，湍流模型为Spalart-Allmaras方程模型。计算域外边界设置为远场条件，给定来流速度、静压和静温等，壁面为绝热无滑移条件。计算全局残差下降6个量级以上为收敛。图3分别给出了2°，5°，8°和12°攻角下前缘的冰型翼型与网格局部放大图。

图3 翼型前缘冰型与网格局部放大图Fig.3 Ice profile and closed view of the mesh close to leading edge

2.2 升阻力系数分析

图4 翼型结冰对气动力影响Fig.4 Influence of Ice accretion of airfoil on the aerodynamic coefficients

图4给出了翼型表面结冰后升阻力系数的变化比较，图中横坐标。对比看出，结冰问题显著降低了该翼型的气动性能。结冰后，各个攻角下的升力系数明显下降，在11°攻角附近最大下降40%左右。阻力系数则有明显增加，最大差别也出现在11°攻角左右。但翼型结冰后，失速点略微后移，在12°攻角时，升力系数达到最大。这是因为由于不光顺冰型，使得翼型吸力面前缘附近就发生了流动分离。图5给出了5°攻角与12°攻角下，压力系数的分布云图，cp表示压力系数。可以看到，随着攻角的增大，分离区的范围扩大。攻角达到12°时，分离区扩展到吸力面三分之一弦长处。而在洁净翼型的分离流动从吸力面尾缘处开始。在12°攻角时分离流覆盖了吸力面后半部分。

图5 前缘附近压力系数云图Fig.5 Contours of pressure coefficient close to leading edge

3 考虑攻角和风速不确定性的CFD模拟

本节采用概率配置点法来研究当攻角和来流风速发生不确定性波动时，对结冰形成的影响以及结冰对气动性能影响，有关非嵌入式概率配点法的详细介绍可以参考文献[19-21]。

3.1 计算设置

仍选取5°和12°攻角为研究工况，分别假设来流风速、攻角分别为服从高斯分布的单个不确定性变量，且风速和攻角同时为服从高斯分布的变量。高斯分布的统计均值与确定性算例的值一致，标准差为设置为均值的10%，计算采用二阶概率配置点法，配置点见表1。

表1 不确定性计算参数设置Tab.1 Settings of stochastic calculations

3.2 计算结果及分析

1）速度不确定性计算结果

图6 速度不确定性对翼型结冰冰型的影响Fig.6 Influence of uncertainty of wind speed on the ice profile of airfoil

图6给出了Case 1和Case 2两个工况下，即存在速度不确定性时翼型前缘结冰冰型的变化。图中给出了三个配置点的计算结果与统计均值的结果，mean value表示统计均值。可以发现，其中从图中可以看出在小攻角下，当来流风速发生波动时，结冰的位置和形状变化不大，但冰层的厚度随着来流风速的增加而明显增大。统计均值的结果与确定性计算的结果几乎完全重合，介于大风速和小风速情况之间。在12°攻角下，结冰的位置变化不大，但是冰型有了一定的变化。大风速下冰层更向压力面侧堆积，前缘处的冰层与其他风速下的冰层厚度基本相同。因此，在大攻角下，冰型对来流速度的随机变化更敏感。

图7给出了5°和12°两个特征工况下升阻力系数的统计均值及置信度为99%的置信区间。图中deterministic表示确定性计算，non-deterministic表示不确定性计算。两个特征工况下升力系数的统计均值与确定性结果基本重合，置信区间关于均值对称。5°攻角下，升力系数的置信区间上下变化约在0.08。随着风速的攻角的增加，上下变化达到0.14。而阻力系数的统计均值略高于确定性结果，置信区间关于均值基本对称。5°攻角下，置信区间上下变化约在0.008。12°攻角时，置信区间上下变化达到了0.012。

图7 速度不确定性对升阻力特性的影响（99%置信区间）Fig.7 Influence of uncertainty of wind speed on the lift and drag coefficients(99%confidence interval)

2）攻角不确定性计算结果

图8给出了5°和12°工况下攻角不确定性对翼型结冰状况的影响。从图中可以看出当攻角发生波动时，即使在小攻角下，翼型上结冰的位置和冰型明显发生了变化。结冰几何外形的不确定性计算统计均值与确定性计算也不再重合，产生了一定的偏差。在下攻角下，冰型的偏差主要体现在最大厚度位置逐渐向翼型压力面移动。在大攻角下，冰型的偏差主要体现在冰层覆盖面积。随着攻角增大，冰层厚度变化趋于平缓。

图8 攻角不确定性对翼型结冰冰型的影响Fig.8 Influence of uncertainty of angle of attack on ice profile of airfoil

图9给出了来流攻角具有不确定性时两个特征工况下升阻力系数的统计均值及99%置信区间。从图中可以看出，在5°攻角下，升力系数的统计均值与确定性计算结果基本重合，其置信区间关于均值对称，上下变化范围约在0.04，明显小于Case 1的情况。而在12°攻角下，统计均值比确定性计算结果低约0.06，置信区间不再关于均值对称，置信区间的上限略大于确定性计算结果，而下限比确定性计算降低了约0.23，有明显的降低。因此，在接近失速的大攻角下，确定性计算低估了结冰对翼型升力的影响。确定性计算结果已表明在给定来流风速的条件下，在12°攻角时翼型升力系数已接近最大（结合图4），来流攻角发生微小波动都会造成升力系数的下降。这与图7的置信区间变化有明显不同，这是因为在Case 1中，随着来流风速不同，升力曲线不再是28.6m/s来流对应的升力曲线。而来流一定的情况下（图8），升力曲线只有一条。从图8(b)中可以看到，攻角的不确定性波动对阻力系数影响较小。大攻角下阻力系数的置信区间的变化大于小攻角下的置信区间的变化。

图9 攻角不确定性对升阻力特性的影响（99%置信区间）Fig.9 Influence of uncertainty of angle of attack on the lift and drag coefficients(99%confidence interval)

3）速度和攻角同为不确定性变量的计算结果

Case 3主要比较同时存在多个独立的随机变量时，各变量的作用是否存在相互影响。图10比较了单个不确定量作用结果线性叠加后与两个不确定性量同时作用的结果下升力系数和阻力系数的标准差。由图可见，两个不确定性量的同时作用的结果略小于直接线性叠加的结果。这说明速度和攻角虽然是独立的随机变量，但二者之间存在物理的耦合作用，削弱了不确定性对翼型气动特性结果的影响。

图10 不确定性量独立作用与同时作用影响比较Fig.10 Comparison of effects of individual and multi-uncertainties

4 结论

本文采用CFD模拟研究了S825翼型结冰对翼型升阻力特性的影响，采用研究了来流风速和攻角的随机变化对翼型表面结冰形状以及结冰后翼型的气动性能的影响。结果表明：

1）与未结冰的洁净翼型相比，结冰后的翼型气动性能严重下降。大攻角下，结冰更容易在叶片前缘与压力面前缘堆积。

2）在来流风速存在随机变化时，冰型的位置和形状变化不大。来流攻角发生变化时，冰型的位置和形状会发生明显变化。

3）大攻角下，来流风速的不确定波动对结冰后翼型的气动性能影响比来流攻角的不确定性波动影响大。在大攻角下，确定性计算会低估攻角对结冰的影响，进而低估对升力系数的影响。风速和攻角的耦合作用削弱了不确定性对翼型气动特性的影响。