复杂建筑火灾中的人员疏散路径多目标规划

张丽杰, 刘建昌, 谭树彬

(1.东北大学 信息科学与工程学院， 辽宁 沈阳 110819； 2. 宁夏理工学院 继续教育学院， 宁夏 石嘴山 753000)

公共场所火灾中的群体性疏散的关键在于路径规划,而复杂建筑路径规划又是多目标优化问题[1].针对不同的路径规划目标,学者们将路径规划问题抽象为一类具有时间约束的网络流问题.Li等[2]提出时延疏散网络路径规划算法.Shen等[3]基于网络流算法构建了宏观疏散路径模型.Li等[4]提出启发式融合算法的网络疏散路径优化模型.Osman等[5]提出集中式混合方法解决网络中的最优路径规划问题.网络流研究多基于疏散网络中每个路段的移动速度不变的假设.很少有研究考虑突发火灾对网络路段通行能力的实时影响.且有研究表明,火灾疏散中,烟雾、气体或热辐射的扩散随时间而动态发展[6].这些动态变化影响疏散人员速度和路段通行能力.文献[7]考虑到各路段受灾害影响,提出基于多目标路径规划模型.文献[8]提出危险预测数据模型来规划建筑发生火灾时最优路径.因此,优化灾害场景的动态路径,实时更新路径选择策略具有重要的意义.本文结合网络流优化和群智能方法,研究了多目标路径优化策略.

1 复杂建筑火灾疏散路径多目标建模

复杂建筑火灾疏散路径优化目标包括空间疏散距离、疏散时间、疏散效率.路径规划需要考虑多个目标的一致性来决策.

1.1 建筑火灾疏散网络问题描述

基于语义特征的网络模化方法,建立面向室内火灾动态多属性特征的疏散网络G(W,E,Te,T,Cw,Ce).疏散网络由节点wi∈W，(i=1,2,…，j)和从节点wi到wj表示的边eij∈E组成,各节点和通道具有多个处于动态变化的属性特征,如边e的疏散时间Te、总疏散时间T、节点w容量Cw、边e的容量Ce等疏散网络特征属性.各节点和通道上的属性特征值随火烟动态表现为时间函数.网络节点特征定义为Wi(wi(xi,yi),ρwi(t),fwi(t)).人员所在位置Wi坐标wi(xi,yi);ρwi(t)为wi在t时刻的人员密度;fwi(t)为wi在t时刻的火烟风险值.边的特征定义为Eij(eij(wi,wj),Teij,dij,fij(t),ρij(t)),在此dij为边eij的当量距离;fij(t)为eij在t时刻的火烟风险值；ρij(t)为t时刻eij上的疏散人员密度.从任意源点S={Sa|a=1,2,…,A}至出口D={Do|o=1,2,…,O}的通道表达为路径集esd∈R.网络中任意的边eij均与建筑空间中具体的疏散路径相对应.

在火灾疏散过程中,个体的运动速度与人员密度和火烟的扩散有密切关系.将火灾产生的有害物质用温度热辐射量、有毒气体扩散度、烟雾能见度标定,建立火烟发展规律和危害物质特征参数关联公式,得到由热量r辐射值FEDr、毒性气体g扩散值FEDg、烟雾s能见度值FEVs构成的火烟风险模型FDSfire.

人员对热辐射的忍受能力主要由周围环境温度决定.整个过程中热量发散值的计算式为

(1)

其中：tIr-k和tIc-k分别为第k个方向上使人员丧失运动能力的热辐射及对流时间;Kr为基准材料燃烧的热量值;α为散布热量的比例系数.其中FEDr在[0,1]范围内取值,当FEDr值不变时,意味着人员已经丧失了逃生能力.

毒性气体对人体的危害取决于燃烧材料散发出的有毒气体的类别、体积浓度和接触时间,燃烧过程中产生毒性气体的计算式为

(2)

其中:Ci为有毒气体i在Δt时间段内的平均体积浓度;(C×t)i为在单位时间t内有毒气体i使人丧失运动行为的体积浓度值;m为有毒的气体种类;Kg为基准材料产生的气体值;α为有毒气体的比例系数.

烟雾中大量的颗粒物质吸收了散射光,能见度受到严重影响.烟雾散布值的计算式为

FEVs=1-Sd/5+Ks.

(3)

其中:Ks为不可见的系数;Sd为单位的可见距离,单位为m.当FEVs大于阈值时,能见度较低,几乎看不清楚周围事物,人员移动速度几乎为0.

建筑物火灾产生的火烟风险对路径的通行能力和人员疏散行为的影响直接体现在走行速度上.受火烟风险影响的通道上的人员移动速度为

FDSfire=FEDr+FEDg+FEVs,

(4)

vij=(1-FDSfire)×vmax.

(5)

其中：vmax为正常疏散时人员在路径上的最大速度;vij为灾害情况下人员在路径eij的走行速度.

受到火烟影响导致通道人流量增加,当人员密度接近通道的瓶颈密度ρc时,移动速度vij为

vij=(1-FDSfire)×vmax×μij,

(6)

μij=[1-αiln(ρi/ρc)] .

(7)

其中:ρi为第i条通道人流密度;αi为第i条通道系数;μij为通道eij流通系数.

1.2 建筑火灾中的疏散路径多目标模型

考虑建筑火灾疏散中的火烟扩散和人员分布等不确定因素,建立最短时间、最低风险和最大疏散容量路径模型,构建疏散路径多目标优化模型为

(8)

其中:N为总疏散人数;F(X)为路径优化目标函数;CT为最小时间T目标函数;Cr为最小风险r目标函数;Cc为最大疏散容量c目标函数.

最短疏散时间路径目标函数为

(9)

最小风险路径目标函数为

(10)

最大容量疏散路径目标函数为

(11)

(12)

满足目标函数的约束条件如下.

疏散网络节点初始状态为

yi(0)=0,∀i∈N.

(13)

疏散网络边的初始状态为

xij(0)=0,∀i,j∈N.

(14)

从源点处疏散的总人数为

(15)

到达目标区域的总人数为

(16)

疏散时间tij的递归方程为

(17)

节点在t时刻的人员容量为

(18)

边在t时刻的人员容量为

(19)

进出疏散网络的人员数量恒定,表达为

(20)

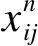
2 基于果蝇算法的多目标路径优化

动态网络路径优化是由最后阶段的路径状态取其最优决策开始计算,直到初始路径达到最优状态为止,即每一步最优解的汇总.路径状态最优方程为

fk+1(i)=min{ck+1(i,j)+fk(i)} .

(21)

其中:fk+1(i)为人员第k+1步从节点wi到目标出口的最小费用;ck+1(i,j)为第k+1步从节点wi到出口wj的费用;fk(i)为第k步从源点到节点wi的费用.

果蝇优化算法(fruit fly optimization algorithm, FOA)中,个体搜索总是跟踪当前种群最优和目前个体最优的解空间寻优,适合解决较大规模网络优化问题.文中将受火烟风险影响的个体移动速度引入疏散模型中,以人员疏散时间、路径风险水平和路径容量为目标,提出改进的自适应果蝇算法(modified adaptive fruit fly optimization algorithm, MAFOA)优化的多目标模型,规划复杂建筑疏散路径.

2.1 多目标果蝇算法设计

果蝇优化算法是基于果蝇觅食行为提出的全局寻优群智能算法[9-11],已被广泛用于解决多目标优化问题.本文利用果蝇算法解决离散问题的特征,研究动态疏散网络路径多目标优化问题,引入速度变量,提出了MAFOA算法.算法如下.

1) 速度和位置更新.MAFOA算法基于二维空间的模型设计,根据果蝇群目标,同一目标区域的群体属于同一子群,将种群分为m个子群.在当前迭代中,人员密度、当前位置和风险水平的不断更新,人员的速度会根据网络参数动态变化而变化.根据人员流动特征,在算法中增加速度调节步长,改进后的速度和位置更新方程为

(22)

(23)

速度分量表达式为

(24)

2) 决策变量.基于MAFOA算法研究疏散问题,将果蝇在疏散网络中的位置表示为二维空间中的变量[12].果蝇代表疏散者,人员的疏散行为是由个体果蝇和果蝇种群来模仿.决策变量的向量X=[x1,x2,…,xn]T表示一群果蝇占据的位置,其维度为人员的数量,向量X即为每个人员的一条路径构成的组合.xi∈Ri,Ri={ri1,ri2,…,rik},i=1,2,…,g.Ri表示第i个待疏散人员可选的g条路径的集合.建筑火灾路径规划属于多目标离散优化问题,在求解路径问题时要把解空间对应到网络路径,即把果蝇种群或个体i在t时刻的位置xt表示为路径集合中的一条可行路径编码.果蝇位置移动对应路径编码变化.

3) 视觉搜索.MAFOA算法视觉搜索用Pareto 解集非支配等级排序方法,优选出果蝇种群所有位置中的两个目标的适宜度值,按照Pareto 解集排序规则分为不同非支配解等级,选择解集中排序等级较低的解,将与之对应的中选个体的位置储存下来逐级迭代.

2.2 疏散过程流程

1) 随机产生疏散人员数量、位置和速度.初始化形成疏散数据网络图G(W,E,Te,T,Cw,Ce),获取节点及边的容量、旅行时间、待疏散人数、起火位置信息,采用Dijkstra算法生成g条路径集合.测定g条路径风险水平和通行容量,与路径疏散时间合并,获得所有人员的可行路径集合.

2) 判断人员是否疏散完毕,如果疏散完毕,更新网络;否则,转到3)进行路径选择.

3) 判断是否分配到新的疏散路径,依据最优路径算法计算路径集,并分配给人员;否则,按照上一步得到的路径方向更新其速度和位置.

4) 根据人员位置判断其疏散状态,如果已经疏散到出口,则n=N-1.

5) 更新未疏散人数系统时间和网络状态,如果n>0,转到2),否则疏散结束.

3 模型应用分析

分别将模型应用于学校综合楼和超市的火灾疏散模拟场景测试.将火灾场景的参数创建为文本文件提供给FDS模型软件,FDS采用直接数值模拟方法,将火灾场景的参数求解后获得的风险值导入仿真系统中.系统从测试对象中提取320个节点和290条边构成疏散网络.人员的初始速度取值为1.3 m/s,每层出口的有效宽度为2 m,出口及走廊人流流通率为1.5人/(m·s-1),出口的通行能力为3.56人/s.算法的参数设置:种群数量为100,子群划分为4组,最大迭代次数200.将文中所建多目标路径规划模型用于不同规模的仿真场景,验证模型的性能.

3.1 算法效率的实现与比较

针对5种规模的网络进行测试,生成60～300个节点的网络数据,对文中提出的MAFOA算法效率与果蝇算法(FOA)、粒子群算法(PSO)、自适应粒子群算法(APSO)进行比较,每组数据运行30次求平均值得到结果见表1.结果表明，MAFOA求解的平均运行时间比其他几类算法的时间少,验证了MAFOA算法在改善建筑火灾疏散性能方面具有可行性.

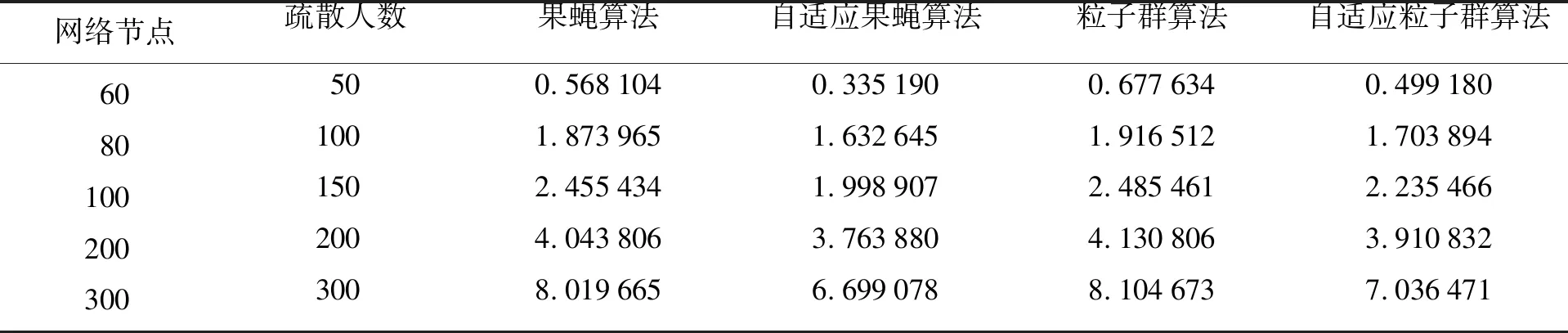
表1 算法运行效率的实现与比较

3.2 目标优化效果分析

算法对160个节点的网络进行单目标和多目标路径规划模型测试,得到路径如表2所示.如果仅考虑最短时间的单目标模型,仅对于疏散人员个体所用的疏散时间是最少的,但是对于整体疏散可能会造成效率下降.多目标路径模型是以整体疏散人员作为考虑对象,虽然在个别情况下结果没有单目标的时间更优,但是从整体疏散效率上达到最优.

表2 两种目标优化出的路径

将单目标优化的最短距离模型、混合模型(最短时间、最短距离)和多目标模型用于相同火灾场景测试总疏散时间,疏散时间如图1所示.结果表明,人流密度比率低于0.4时,最短距离模型的疏散效率较高;当达到0.6的瓶颈密度后,多目标模型的时间最短,单目标最短距离模型在临界密度状态下基本不起作用.反映了多目标模型在环境复杂的较大规模疏散中具有优势.

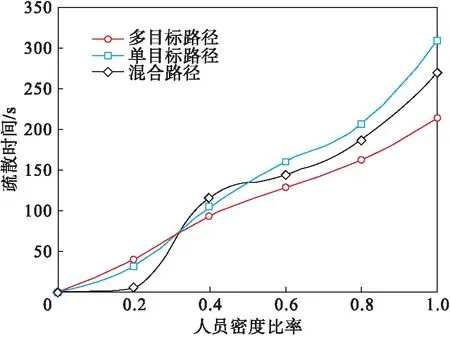
图1 不同路径模型的疏散时间

3.3 疏散过程仿真分析

将模型用于3 500 m2一层布局的超市模拟疏散过程,出口1，6为2 m,其余4个出口5 m.场所内随机分布为1 700人.起火点1位于中心位置,起火点2位于靠近出口6的位置.疏散过程如图2所示,反映了系统时间为35，70，90，115 s场景中人员疏散状态,体现了多目标路径规划与实际疏散目标的一致性.过程中合理利用了场景可用资源,实时跟踪疏散环境数据,动态调整路径利用率.验证了复杂建筑火灾中疏散路径多目标优化策略的合理性.

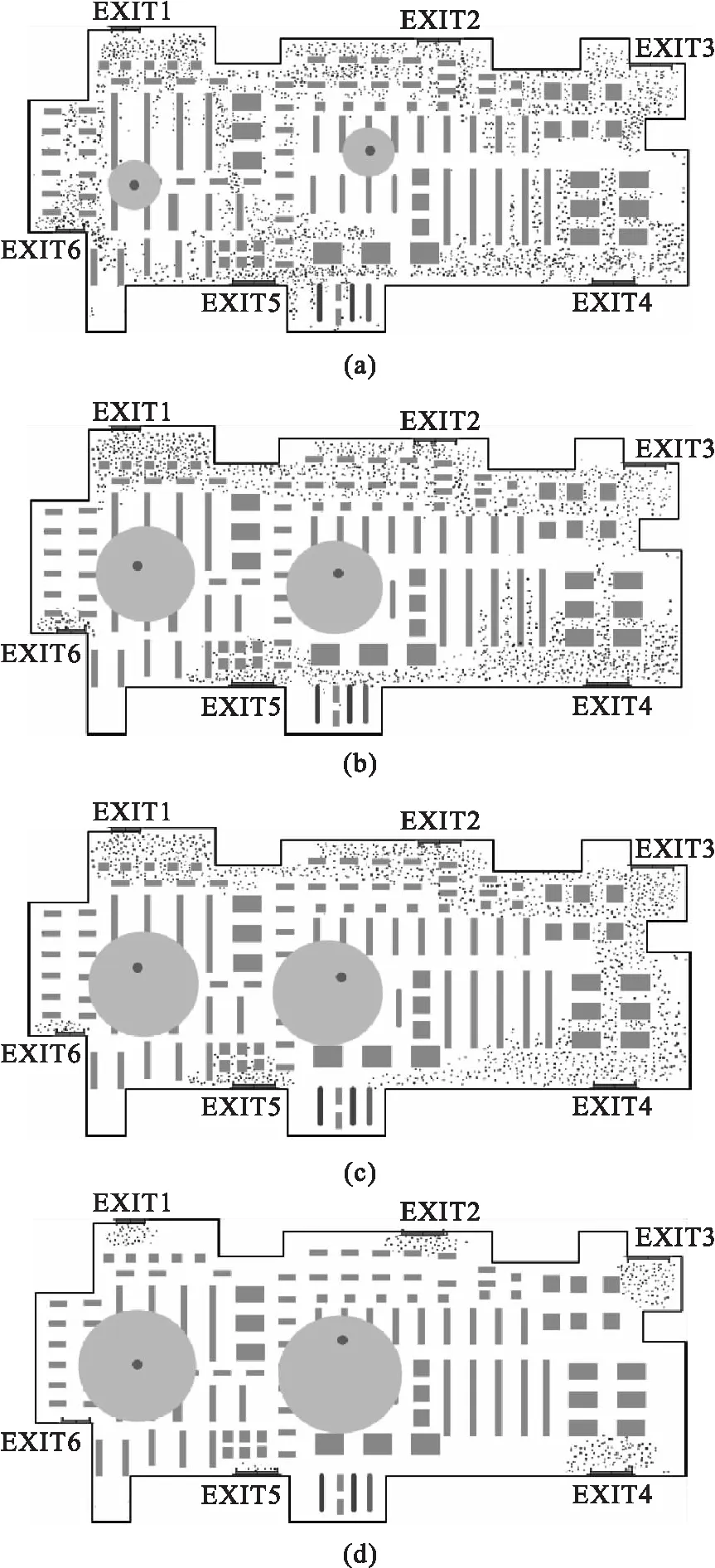
图2 疏散过程

4 结 论

1) 验证了基于MAFOA多目标路径规划处理较大规模的建筑火灾疏散问题具有一定优势;多目标路径规划适用于环境复杂的疏散场景.

2) 揭示了复杂建筑火灾中的人员疏散行为机理和路径选择过程.