SSA:一种面向CQF模型的TSN资源调度算法
姜旭艳, 严锦立, 全 巍, 孙志刚
(国防科技大学 计算机学院, 湖南 长沙 410073)
工业控制网络和5G网络中包括时间敏感流、带宽约束型流量和Best-Effort流量,其中优先级最高的时间敏感流通常具有周期性的特点,对端到端延迟和抖动有着严格的要求,延迟通常在毫秒级别[1].例如在能源开采应用中,网络时延在250 μs~1 ms之间,抖动不能超过1μs.如果不能保证服务质量(quality of service,QoS),整个生产过程就会失败,甚至导致系统瘫痪.因此,保证时间敏感流量的服务质量对系统的安全稳定运行至关重要[2].
标准以太网是竞争性网络,数据传输由于排队等因素具有不确定性,只能提供尽力而为的服务,无法保证时间敏感流的服务质量[3].IEEE 802.1时间敏感网络任务组提出的实时以太网技术——时间敏感网络(TSN),利用全局时间同步、确定性分组转发、帧复制及冗余消除等技术为时间敏感流提供低延迟、低抖动的确定性传输服务[4],目前已经逐渐应用到工业控制领域和5G网络中.保证TSN性能的关键在于时间同步和资源调度,时间同步是保证服务质量的前提,资源调度是实现确定性传输的关键.目前时间同步已有详细的标准及算法,而资源调度在不同的调度模型和应用中存在很大差异.随着网络规模不断增长、应用需求愈发复杂,研究高效的TSN资源调度算法对TSN的大规模应用具有重要意义.
资源调度主要包括数据平面的调度模型和控制平面的调度算法,调度算法根据约束条件将调度模型的资源(如队列资源、时隙资源、带宽资源等)合理分配给网络中的时间敏感流和其他类型的流量,同时要最大化网络资源利用率.资源调度问题可以归纳为一个装箱问题,即从时间和空间两个维度上合理地为报文分配链路资源,因此是一个NP完全问题[5].
现有的资源调度模型主要包括TTTech公司提出的时间触发以太网(time-triggered Ethernet,TTEthernet)中的交换模型和TSN中的时间感知的整形器(time aware shaper,TAS).TTEthernet根据静态的调度表(schedule table)对时间敏感流进行逐跳的转发控制.TAS的原理类似于TTEthernet中的调度表,但TTEthernet调度的粒度是数据流,而TAS调度的粒度则是队列.控制平面的调度算法包括SMT Solver、OMT Solver、ILP Solver和禁忌搜索算法等[6-8],这些算法虽然能够得到可行的调度方案,但是逐跳地分配链路资源的计算复杂度通常较高.为了降低复杂度,通过对TAS进行简单配置,提出了循环队列转发模型CQF.CQF根据奇偶时隙进行队列切换,每个时隙只有一个队列能够传输报文,另一个队列用于接收报文.目前缺乏基于CQF模型的资源调度算法.
1 相关研究
工业控制网络中的实时数据交换从基于总线的交换向以太网交换演进,标准的以太网技术无法满足实时系统的要求,在标准以太网的基础上发展起来的时间敏感网络TSN和时间触发网络TTEthernet能够为系统中的时间敏感流提供低延迟、低抖动的传输服务.
在TSN和TTEthernet中,关于资源调度问题的研究主要从数据平面的调度模型和控制平面的调度算法两个方面展开.调度模型实现确定性转发机制,向控制平面提供可配置的资源.控制平面则根据流量及调度模型的特征构建约束条件,使用调度算法求解可行的调度方案,根据调度方案对数据平面进行配置.文献[5,8-10]采用SMT为TTEthernet中的时间敏感流寻找满足约束条件的可行解,文献[11]则采用Tabu搜索算法寻找最优的调度方案.所有流量特征是预知的,离线地计算满足网络约束(链路资源、交换机资源、端到端延迟等)和应用约束(发送依赖等)的调度方案,为每个数据帧规划沿路由路径的每个交换机上的发送时刻.
TSN的TAS调度模型对应的调度算法是在满足约束条件的前提下配置控制每个队列传输开关的时间门控表.文献[6]发现TAS中存在输出端帧交错的问题,需要增加队列隔离、流隔离等方式解决,并采用SMT找到满足约束的可行解.除此之外还提出使用OMT,通过设定最优化目标,求解满足约束条件的最优解.文献[1,7]则使用ILP建模求解调度问题.除此之外,为了解决大规模网络下的调度问题,文献[7]提出基于Tabu的启发式算法以降低计算开销.上述这些方法都是基于TAS模型提出的调度方案,而对于CQF模型,目前缺乏相应的资源调度算法.本文将CQF模型中的调度问题抽象为多约束条件下的资源规划最大化问题,提出了一种基于起始时隙分配的轻量级的资源调度算法SSA.SSA借鉴了贪心算法的思想,与TAS中使用启发式方法的调度算法相比,计算开销低.除了贪心算法之外,也可以使用其他方法,例如Tabu搜索算法、SMT等工具求解本文提出的多约束条件下的资源最大化问题.
TSN和TTEthernet中不同调度模型所对应的调度算法的特点及解决方案如表1所示.
2 研究动机
IEEE 802.1Qch提出的循环队列转发模型是对IEEE 802.1Qci per-stream filtering and policing(PSFP)和IEEE 802.1Qbv time aware shaper(TAS)的一种简单配置,它通过流量整形为关键数据流提供确定且易于计算的延迟服务[7].PSFP提供过滤、分类和流量监管功能;TAS提出了门控机制,队列后面的门结构根据门控列表(gate control list)指定的时隙来改变状态.
CQF由一个循环定时器(cycle timer)和两个传输队列构成.在CQF模型中,全局时间被划分为等长的时隙,数据传输需要遵循以下两条规则:1)上游交换机传输报文的时隙与下游的邻居交换机接收报文的时隙相同;2)交换机在某个时隙内接收的报文一定会在下一个时隙传输出去.基于上述两条规则,奇数时隙,队列Q7保存输入端口接收的帧(接收模式,不发送帧),同时队列Q6发送在上一个偶数时隙缓存的数据帧(发送模式,不接收帧),如图1a所示;偶数时隙,操作相反,如图1b所示.
基于上述传输方式,CQF可以确定报文的延迟范围.假定时隙长度为d,链路速率足够大,交换机SWi要将报文msg传输给下游的邻居交换机SWj.在最坏情况下,若SWi在时隙slotk的开始时刻将报文msg传输到SWj,SWj在时隙slotk+1的结束时刻将msg传输出去,那么msg在这两个交换机之间的延迟就是2d;在最好情况下,若SWi在时隙slotk的结束时刻将msg传输到SWj,SWj在时隙slotk+1的开始时刻(即时隙slotk的结束时刻)将msg传输出去,那么msg在这两个交换机之间的延迟就是0.将上述情况一般化,假定h为跳数(路由路径上的交换机的数目),那么一个帧的最大延迟maxDelay和最小延迟minDelay即
maxDelay=(h+1)d,
(1)
minDelay=(h-1)d.
(2)
换言之,一个帧的端到端延迟范围由时隙长度和跳数确定.
图2a所示TSN网络中包含三个终端host1、host2和host3以及一台交换机SW1.假定时隙长度为150 μs,交换机的输出端口中每个CQF队列的长度均为3.2 kB.网络中有f1,f2,f3三条时间敏感流,流的信息如图2b所示,假定三条数据流均从0时刻开始传输.
若不采用任何调度策略,将三条流的传输用甘特图表示,如图3a所示.根据CQF的传输规则(1)和传输规则(2),上游交换机在时隙sloti内发送的帧会在相同的时隙内,即时隙sloti内被相邻的下游交换机接收,下游的邻居交换机在时隙sloti+1将该帧传输出去.数据流f3第0个周期的报文f3,0在host2的第0个时隙slot0送往SW1,SW1本应该在时隙slot0将f3,0缓存到CQF队列,并在第1个时隙将f3,0发往host3.但在SW1的时隙slot0内,报文f1,0和f2,0已经占用了1000 Bytes+1200 Bytes=2200 Bytes的队列资源,SW1在时隙slot0上可用的队列资源即3200-2200 Bytes=1000 Bytes,小于f3,0的帧长1500 Bytes,SW1只能丢弃f3,0,所以f3,0无法在时隙1传输到host3.

图2 简单网络拓扑及流实例
虽然SW1在slot0内的队列资源有限,但在slot1内队列资源充足,因此,可以将f3,0的发送时间往后偏移一个时隙,从而提高资源利用率.如果f3,0能够在slot0被SW1缓存,并在时隙slot1被SW1送往host3,根据CQF的最大延迟计算公式(1),其最大的端到端延迟为(1+1)×150 μs=300 μs.那么将f3,0往后偏移一个时隙后,其最大的端到端延迟即300 μs+150 μs=450 μs,小于其允许的最大端到端延迟750 μs,因此将f3,0的发送时间往后偏移一个时隙是可行的.将三条流的传输用甘特图表示,如图3b所示.值得注意的是,f3,0偏移发送时间后的最大端到端延迟变成了450 μs,但f3其余报文的最大端到端延迟为300 μs,会在host3上造成抖动,所以将f3所有报文的发送时间都往后偏移一个时隙.
综上所述,合理地在源端偏移时间敏感流的发送时隙,可以提高网络资源的利用率.本文根据以上发现,设计基于起始时隙分配的资源调度算法,从而最大化能够成功调度的流的数量.
3 系统模型
本文将TSN网络的拓扑抽象为无向图,用G表示网络拓扑,G={V,E}.V表示网络节点的集合,V=SW∪H,其中SW表示交换机的集合,H表示终端的集合.E表示连接两个网络节点的边的集合.交换机的每个输出端口包含8个队列,其中优先级最高的两个队列用作CQF队列,用于缓存时间敏感流,其余队列缓存低优先级的流量.本文只讨论时间敏感流的调度,所以只对CQF队列资源的调度进行讨论.图4所示的Q7和Q6即交

图3 TSN调度传输示意图
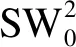
终端是数据流的来源及目的地,它对每条流报文的发送时隙进行配置,调度器Scheduler根据配置信息和全局时钟调度缓存队列Buffer中的报文,如图4中的终端H0所示.终端也能够对数据流进行准入控制,数据流被标记为无法调度时,调度器不会调度属于该数据流的帧.如果属于同一条流的数据帧的偏移量不同,那么它们的端到端延迟也不同,从而产生抖动,因此本文假定数据同一数据流的所有数据帧在源端的发送偏移量相同.交换机和终端均使用IEEE 1588 Precision Time Protocol(PTP)进行全局的时间同步,时隙的长度是相同的,并且是固定的.某个时隙内,终端H0和交换机SW0内的数据传输情况如图4所示.

图4 系统模型
时间敏感流是周期性的[6,12],属于同一条流的两个数据帧之间的最小发送间隔即为该流的周期,每个周期发送的数据量是固定的.假定流的信息是已知的,流在每个周期只发送一个报文,并且在0时刻就开始产生数据.用包含源端、目的端、发送周期、每个周期的数据量大小、传输路径和允许的最大端到端延迟的六元组来描述数据流:
fi={fi.src,fi.dest,fi.period,fi.size,fi.path,fi.deadline}.
(3)
fi∈F,用fi,j表示fi的第j个数据帧.由于属于一个数据流的所有数据帧在源端的偏移是相同的,因此用fi.offset表示数据帧从源端发送时对应的时隙.本文的调度粒度是交换机输出端口上的CQF队列,因此在描述传输路径时需要携带传输端口.用fi传输经过的交换机端口来表示路径,那么路径的表达式如下:
(4)

根据CQF的传输规则,对时隙长度lenOfSlot进行分析.由于以时隙为基本单位对数据进行偏移,假定lenOfSlot能够整除所有数据流的周期.将所有数据流的周期记作P,P={f0.period,f1.period,…,fn.period},那么最大的时隙长度为
MAX(lenOfSlot)=GCD(P) .
(5)
即lenOfSlot的最大值为数据流周期的最大公约数.CQF规定,报文在相邻两个节点的发送时隙与接收时隙相同.那么,时隙的长度至少需要保证队列中的最后一个报文在相邻节点之间的发送时隙与接收时隙相同,因此最小的时隙长度为

(6)

4 问题描述
时间敏感流是周期性流量,正常情况下会循环往复地运行,直接计算出数据流在无限个时隙内的传输计划是不现实的.考虑到数据流的传输也是周期性的,因此在描述约束条件前,需要确定调度周期T.只要在T内数据流的传输符合约束条件,那么在整个过程中流的传输都符合约束条件.一般情况下,数据流周期的值是任意的,因此,将调度周期T设置为所有流的周期的最小公倍数,即T=LCM(P).这样,调度计划每隔T循环执行一次即可.在上述假设下,数据流的传输主要包括以下4个约束条件.
约束1:帧发送偏移
每个数据帧在源端的偏移量以时隙为单位.偏移量应不超过每个周期内时隙的数量,即
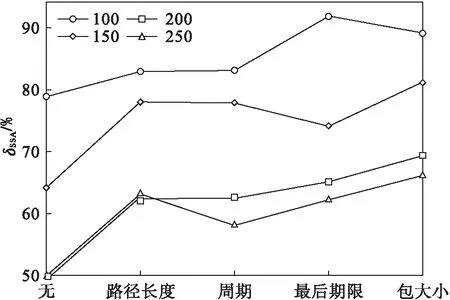
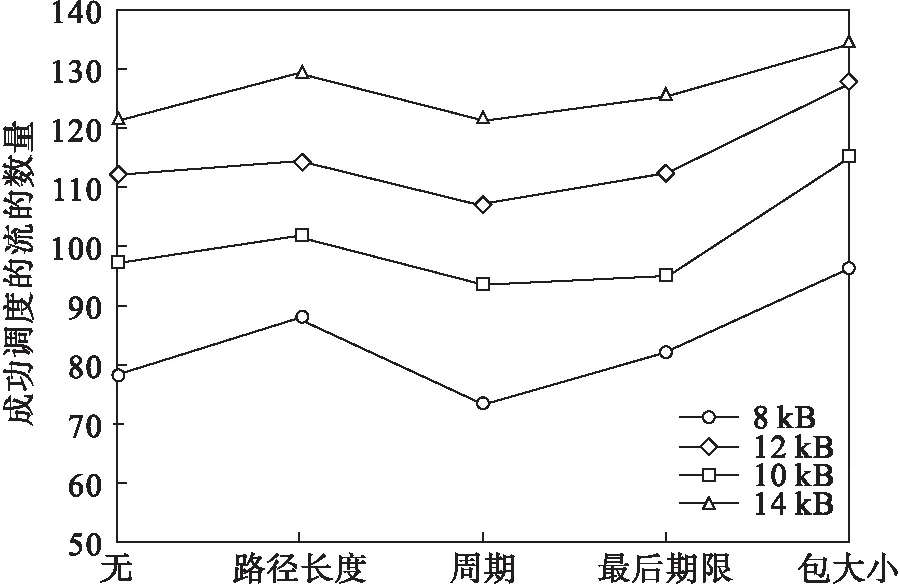
fi.offset (7) 在源端偏移时隙,可以提高资源利用率,但是,当偏移量过大时,下一个数据帧已产生,上一个数据帧却还未发送,终端上需要缓存大量的数据帧,耗费的存储开销大. 约束2:端到端延迟约束 TSN必须要保证服务质量.因此,在发送端偏移的时隙加上CQF模型最大的延迟不能超过该数据流允许的最大端到端延迟,即 fi.offset×lenOfSlot+(fi.hop+1)×lenOfSlot≤fi.deadline . (8) 其中,fi.hop为数据流从源端至发送端的总跳数. 约束3:接收窗口约束 根据描述的CQF传输规则(1),上游交换机发送报文的时隙应该和相邻下游交换机接收报文的时隙相同.满足CQF传输规则的最小的时隙可以保证该约束. 约束4:队列资源约束 交换机输出端口的缓存队列的资源是有限的.换言之,某段链路在一个时隙能够传输的时间敏感型数据帧的数量是有限的,在这个时隙内传输的数据的总长度不应该超过缓存队列的长度.若流fi的第j个报文在时隙t经过SWk的端口l,则O(i,j,k,l,t)=1,否则为0.队列资源约束的形式化描述如下: (9) t与i,j,k,l之间存在如下关系: 在满足上述约束条件的情况下,算法要使能够调度的流的数量最大化.因此,链路时隙分配问题实际上是一个优化问题. 根据资源调度模型和约束条件,提出了基于起始时隙分配的资源调度算法,如算法1所示. 算法1 SSA调度算法 输入:F,G 输出:F.OFFSET BEGIN 1T=compute_LCM(P); 2F=flow_sort(F); 3 FOREACHfiINFDO: 4 FOREACH offset IN[fi.period-1,0] DO: 5 latency=count_e2e_latency(fi,offset,slot_cycle); 6 IF latency 7fi.flag=sw_queue_constraint(fi,G,T); 8 IFfi.sched_flag==SUCCESS THEN: 9 update_global_resource(fi,G,T); 10 BREAK; 11 ELSE 12 CONTINUE; 13 END IF 14 ELSE 15fi.sched_flag=FAIL; 16 CONTINUE; 17 END IF 18 END FOR 19 END FOR END 首先,计算调度周期(第1行),调度周期T为所有时间敏感流的周期的最小公倍数,调度方案在这个周期内循环执行.接着,按照设定的参数(路径长度、报文大小、允许的最大端到端延迟、周期大小)进行排序(第2行),位置靠前的数据流优先分配资源.然后,按照既定的顺序为数据流分配资源(第3~19行).4个约束条件中,帧发送偏移约束对应第4行,端到端延迟约束对应第5行和第6行,队列资源约束则对应第7行.为了让CQF模型能够正常传输报文,用户设定的时隙一定大于允许的最小时隙长度,接收窗口约束得到满足. 算法借鉴了贪心算法的思想.对流进行排序时(第2行),优先映射占用资源较少的数据流,根据这一思想提出了4种贪心策略,即按照路径长度升序、报文大小升序、允许的最大端到端延迟升序、周期大小降序的方式调整流的顺序.以报文大小升序为例,排序后,每次映射时选择的总是当前尺寸最小的报文.在源端对时隙进行偏移时,采用偏移量递减的贪心策略,从最大的偏移量对数据流进行映射(第4行),为后映射的流保留位置相对靠前的时隙. 目前应用TSN的工业控制网络中,大多是环形拓扑,例如环形以太列车网络(Ethernet train bone,ETB).因此,本文模拟搭建了一个环形网络,如图5所示. 图5 环形网络拓扑 环形网络中包括7个支持CQF转发模型的TSN交换机,每个交换机连接的终端数量从集合{1,2,3}中随机选择,时隙长度设置为125 μs.网络中时间敏感流数量从集合{100,150,200,250}中选择.由于目前没有开源的支持TSN测试的数据集,文中的数据流为随机产生.每条数据流中每个周期产生的报文数量为1.数据流的周期长度为时隙的整数倍,周期范围为2~9个时隙,报文大小在64~1 500 Bytes之间,允许的最大端到端延迟至少要大于CQF的最大端到端延迟.在上述场景中运行SSA,为时间敏感流计算出调度计划,并根据调度成功率对算法的质量进行评估. 不在发送端控制帧的发送时隙,先映射的流先分配队列资源,队列资源不足时直接将流标记为不可调度,称这种调度方式为直接调度(direct scheduling,DS).接下来从不同的维度展示SSA的调度效果,并对实验结果进行分析. 将交换机CQF队列的长度均设置为15 kB,在上述实验场景中分别生成100,150,200,250条数据流,按照不同的参数对流进行排序(周期降序、数据帧大小升序、路径长度升序、允许的最大端到端延迟升序),使用SSA计算调度方案,统计调度成功率.同时,计算DS成功率,与SSA进行对比,如图6所示.不论使用何种排序方式,SSA的调度成功率均高于DS.计算得到,SSA能够使DS的调度成功率平均提高41.84%. 图6 SSA调度与DS调度的对比 在偏移源端的发送时隙时,采用了偏移量递减的贪心策略.为了验证这种方式的有效性,本文设计了偏移量递增的分配方式.在上述实验场景中生成了200条数据流,CQF队列长度同样为15 kB,分别运行两种算法,结果如图7所示.偏移量递减比偏移量递增的调度成功率平均高3.89%,偏移量递减的调度方式比不调整偏移量的调度方式的调度成功率平均高18.32%.与按照偏移量递增的方式相比,偏移量递减的方式能够为周期较小的报文留下调度周期中相对靠前的时隙,因此调度成功率比偏移量递增的方式高.在周期大小降序的流映射方式中,与偏移量递增相比,偏移量递减的方式能够将调度成功率提高9.65%.按周期大小排序,位置靠后的报文的周期小,可选择的偏移量的范围也小,周期大的报文占用了靠后的时隙,留下了相对靠前的时隙资源,因 图7 offset升序与降序的对比 此调度成功率得到明显提高. 为了研究队列资源对调度成功率的影响,本文调整队列长度,将CQF队列长度分别设置为8,10,12,14 kB,生成200条数据流,统计调度成功的流的数量,如图8所示.实验表明,随着队列资源的增多,调度成功率也随之提高.CQF队列长度相同时,4种排序方式之间进行对比,按照报文大小排序的调度成功率远大于其他4种方式,即报文大小对调度成功率的影响最大. 图8 队列长度对成功调度的流的数量影响 将队列长度分别设置为2,4,6,8,10,12,14,16,18,20 kB,采用包大小升序的排序方式、偏移量降序的调度方式,计算200条时间敏感流的成功调度的数量,实验结果如图9所示.本文设定时隙长度为125 μs,在千兆以太网中,一个时隙可以传输的最大的时间敏感流大小为15.625 kB.在时隙长度不变的情况下,当队列长度小于15.625 kB时,增长队列长度,相当于增加分配给时间敏感流的带宽,如图9中的理论带宽所示,那么能够成功调度的流的数量也随之增加.当CQF队列的长度超过15.625 kB时,由于链路速率的限制,即使再增加队列长度,调度成功率也不会继续增长. 图9 带宽资源对成功调度的流的数量影响 本文研究发现,在基于CQF模型的资源调度中,需要从时间维度上对资源进行分配.如果在端系统上直接发送数据流,某些时隙内的流量会超过队列长度,而在另一些时隙中存在大量的空闲队列资源.通过延迟端系统的发送时间,可以利用这些空闲资源,成功调度更多的流量.为此,本文将基于CQF模型的资源调度问题抽象为多约束条件下的资源规划最大化问题,将约束条件归纳为:1)帧发送偏移约束;2)接收窗口约束;3)端到端延迟约束;4)队列资源约束. 本文借鉴贪心算法思想,提出了基于起始时隙分配的资源调度算法(SSA),通过对端系统的时隙进行调度,提高队列资源利用率,以最大化成功调度的流的数量.本文分别从周期、报文大小、路径长度、允许的最大端到端延迟4个角度出发,提出了4种贪心策略,使占用资源少的报文能够被优先调度. 本文构建了工业控制网络中典型的环形网络拓扑对算法的有效性进行评估,通过与不控制发送时隙的分配策略相比,本文提出的SSA算法平均可以提高41.84%.通过对4种策略的对比结果发现,报文大小对资源调度的影响最大.
5 算法描述
6 实验评估
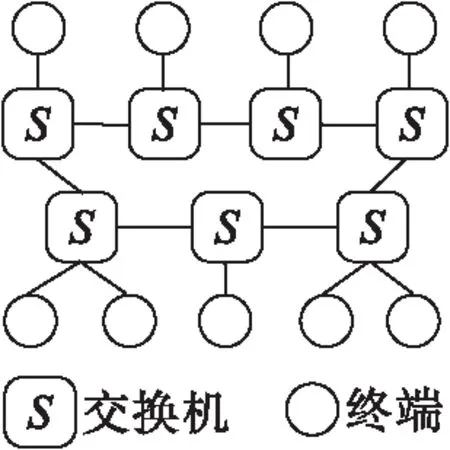
6.1 实验场景
6.2 实验对比与分析


7 结 语

