碳纤维丝缠绕无人机毁伤效能分析

马珊珊，张跃跃，张会锁

（中北大学机电工程学院， 太原 030051）

0 引言

随着科技的进步，旋翼类无人机的发展越来越快，随之带来的安全性问题也越来越多。此类无人机因其隐蔽性强、可获得性容易、升空突然、易操控、反射截面小，成为防控的重点和难点［1］。尤其是在城市作战环境下，人口密度大、建筑物密度高、电磁和交通等环境复杂，对于无人机的防范、处置十分困难，而传统的硬毁伤拦截无人机方式在城市环境中并不适用。

一些科研机构对此展开了研究。冯顺山等［2］提出了一种等待式拦截低空慢速小目标的方法，该方法在大型会场中可有效拦截旋翼类无人机。本文正是基于此拦截机理，针对碳纤维丝形状（横截面为矩形和圆形），对无人机螺旋桨缠绕性能进行仿真研究，所得结论可为反无人机毁伤元的选则提供依据。

1 碳纤维丝缠绕无人机毁伤机理

常规的反无人机方法有：摧毁发射平台、伪装欺骗、电磁干扰、直接火力打击、激光武器等［3］，但这些方法通常都伴随着附带损伤，在复杂的城市环境中并不适用。

利用碳纤维丝缠绕无人机的方法主要针对的是“低慢小”旋翼类飞行器，它是一种通过探测系统、指控系统、拦截系统来对目标进行拦截的软毁伤方式，在大型活动的安保工作中［4］或禁止飞行区域中可以有效地防御不明无人机的侵入，并可避免不必要的人员和财产等损失。

如图1所示，碳纤维丝软毁伤旋翼类无人机的原理与渔网或水草缠绕船舶螺旋桨的原理异曲同工。

图1 水草缠绕船舶螺旋桨Fig.1 Diagram of seaweed wrap ship propeller

当碳纤维弹飞至目标后，打出若干纤维丝团，丝团展开成若干排，形成拦截幕。向前飞行的无人机由于惯性力来不及调转方向而撞入拦截幕中，其螺旋桨此时很容易被纤维丝所缠绕。螺旋桨阻力矩将增大，从而造成发动机负荷增大，甚至超负荷工作，严重时可能造成轴系、螺旋桨蹩停，发生螺旋桨桨叶变形、损坏等故障，导致无人机失稳、运动轨迹改变甚至坠毁，进而达到防御无人机的目的。

由于无人机螺旋桨叶片形状的不规则性、碳纤维丝为柔性材料且表现为各向异性以及无人机在飞行过程中气流的复杂性，目前还未见关于对碳维丝缠绕无人机螺旋桨过程理论计算分析的相关文献报道。本文利用有限元分析软件，通过数值仿真的方法定性地分析了纤维丝对无人机的缠绕效果。由空气动力学可知，不同形状的物体在空气中运动时的空气阻力系数不同。与圆形纤维丝相比，在相同迎风面积下，矩形纤维丝阻力系数较大，减缓了纤维丝团的展开速度，且增加了其漂浮时间，延长了拦截时长。然而，二者对无人机的拦截效果尚未可知。故对两种形状的纤维丝缠绕无人机的过程进行数值仿真分析，以期选出更优的纤维丝形状。

2 数值仿真

2.1 模型建立

考虑到无人机螺旋桨叶片形状的不规则性及飞行环境的复杂性，对无人机模型及其环境进行简化：1）由于纤维丝主要缠绕毁伤无人机螺旋桨，故模型只取螺旋桨部分；2）假设碳纤维丝团已成展开状态，并忽略空气流动的影响。简化后的模型如图2所示。

图2 模型示意图Fig.2 Diagram of model

如图3、图4所示，为比较不同截面形状纤维丝对无人机螺旋桨的缠绕效果，分别建立了圆形和矩形截面的纤维丝（横截面积、长度、密度均相同）有限元几何模型，图5为螺旋桨有限元几何模型。

图3 圆形截面纤维丝有限元几何模型Fig.3 Finite element geometric model of circular section fiber wire

图4 矩形截面纤维丝有限元几何模型Fig.4 Finite element geometric model of rectangular section fiber wire

图5 螺旋桨有限元几何模型Fig.5 Finite element geometric model of propeller

2.2 材料属性

无人机螺旋桨比纤维丝刚度大很多，故简化模型将螺旋桨视为刚体。

在ABAQUS软件中，按照材料刚度与方向的关系将材料线弹性分为4类：各向同性、各向异性、正交各向异性、横观各向同性［5］。碳纤维丝为柔性体，且表现为各项异性，但考虑到本文仿真中碳纤维丝横截面为规则几何形状，故认为碳纤维丝为横观各向同性材料，并作以下假设［6-7］简化材料模型来确定纤维丝材料参数：

图6 0.3ms 时刻圆形纤维丝缠绕结果Fig.6 Winding results of circular fiber wire at 0.3ms

1）纤维丝各方向泊松比为0；

2）纤维丝各方向剪切模量均相等。

由此给出纤维丝材料参数［8-9］，如表1所示。

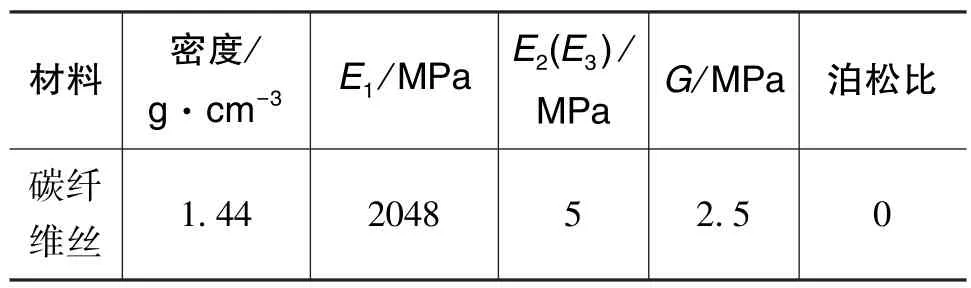
表1 纤维丝材料参数Table 1 Parameters of fiber wire material

2.3 边界条件

1）因缠绕过程时间很短，故视纤维丝处于静止状态。给予纤维丝自由态，不限制其任何自由度，来模拟纤维丝团展开后状态，即垂直摆成一排（为简化模型，将其假设为垂直状态）漂浮在无人机面前。

2）设置预定义场：赋予螺旋桨 830r/s（电机最大转速）的初始旋转速度以及15m/s（无人机最大速度）的前行速度，以此来模拟无人机的运动。

2.4 仿真结果及分析

经ABAQUS/Explicit显示积分求解器［10］求解，得出了不同时刻圆形纤维丝、矩形纤维丝缠绕螺旋桨的仿真结果。图6、图8、图10、图12分别为圆形纤维丝在0.3ms、1.2ms、3ms、10ms时刻缠绕无人机螺旋桨的结果，图7、图9、图11、图13分别为矩形纤维丝在上述不同时刻的缠绕结果。

图7 0.3ms 时刻矩形纤维丝缠绕结果Fig.7 Winding results of rectangular fiber wire at 0.3ms

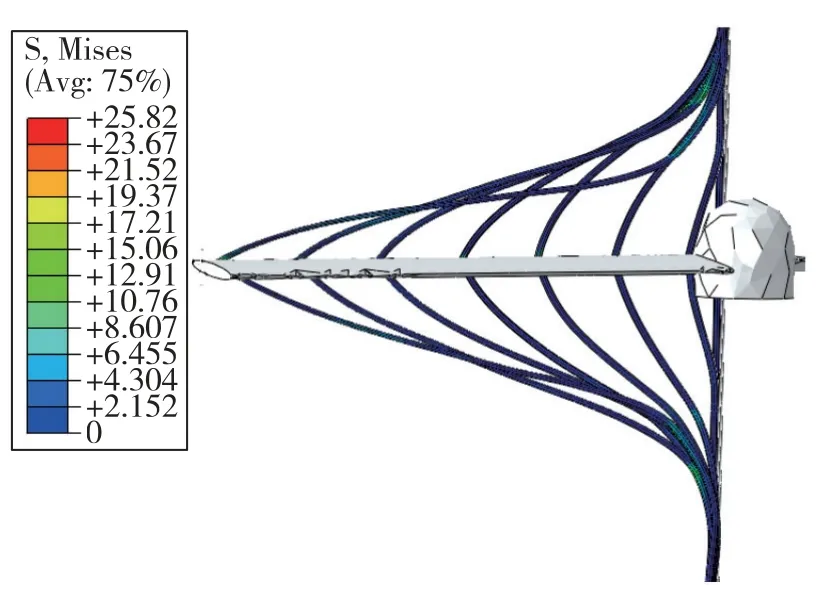
图8 1.2ms 时刻圆形纤维丝缠绕结果Fig.8 Winding results of circular fiber wire at 1.2ms

图9 1.2ms 时刻矩形纤维丝缠绕结果Fig.9 Winding results of rectangular fiber wire at 1.2ms

图10 3ms 时刻圆形纤维丝缠绕结果Fig.10 Winding results of circular fiber wire at 3ms

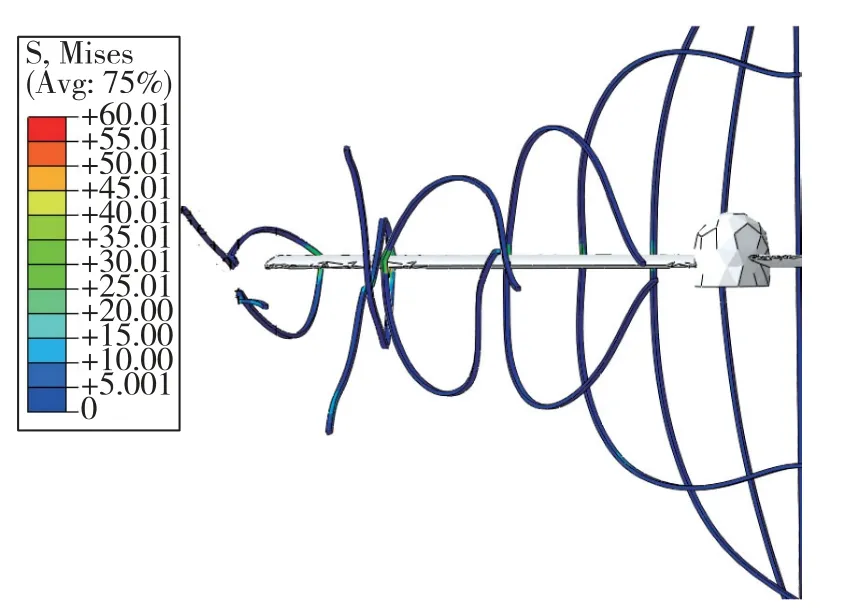
图11 3ms 时刻矩形纤维丝缠绕结果Fig.11 Winding results of rectangular fiber wire at 3ms

图12 10ms 时刻圆形纤维丝缠绕结果图Fig.12 Winding results of circular fiber wire at 10ms

图13 10ms 时刻矩形纤维丝缠绕结果图Fig.13 Winding results of rectangular fiber wire at 10ms

由图6～图13的等效应力图可知，圆形纤维丝与矩形纤维丝对螺旋桨均有缠绕效果，但是效果有所差别。在每个时刻，二者所受应力趋势一致，但是矩形纤维丝最大应力处所受应力大于圆形纤维丝最大应力处所受应力。由此，可得出矩形纤维丝给予无人机螺旋桨更大的反作用力。

螺旋桨旋转速度与前进速度随时间的变化曲线如图14、图15所示。

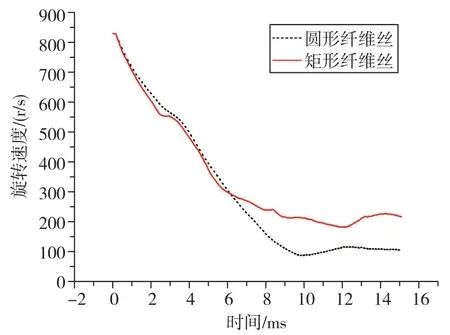
图14 旋转速度随时间变化曲线Fig.14 Curves of rotation speed with time

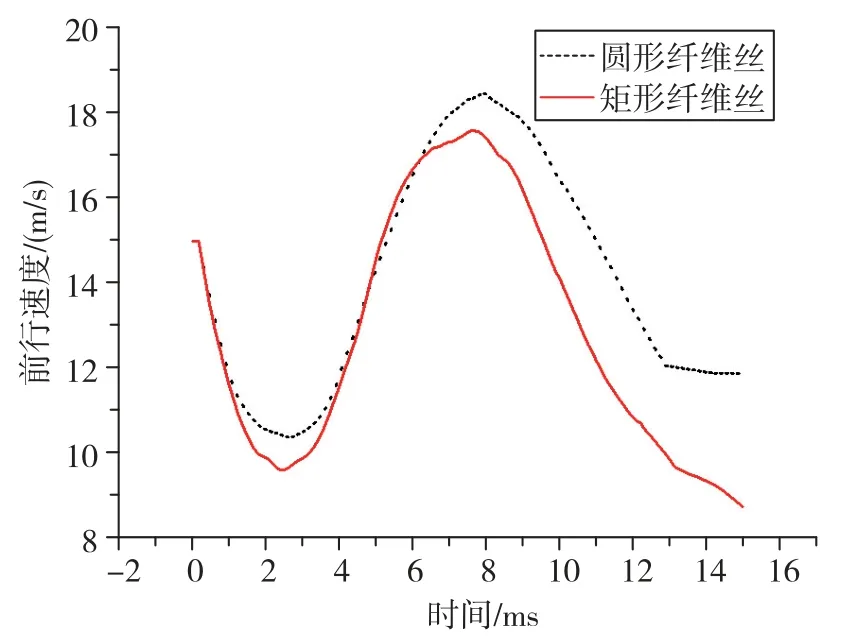
图15 前行速度随时间变化曲线Fig.15 Curves of forward speed with time

由图14可知，当螺旋桨与圆形纤维丝或矩形纤维丝撞上后，螺旋桨的旋转速度基本上都是呈线性下降的。矩形纤维丝缠绕效能在6ms时刻开始减弱，旋转速度逐渐趋于200r/s；而圆形纤维丝缠绕效能则是在9ms时刻开始减弱，旋转速度趋于100r/s。可见，从旋转速度下降效果来看，圆形纤维丝优于矩形纤维丝。

由图15可知，当螺旋桨与圆形纤维丝或矩形纤维丝撞上后，前行速度的下降趋势是一致的。一开始前行速度下降，之后由于受到纤维丝的反作用力，前行速度变大；随着螺旋桨旋转，后期又受到纤维丝的阻力，前行速度又下降。可见，从前行速度下降效果来看，矩形纤维丝对螺旋桨的影响较大。

3 结论

对“低慢小”的旋翼类飞行器所带来的安全隐患，选择用碳纤维丝缠绕毁伤无人机可以减小传统反无人机方法带来的附带损伤。

运用ABAQUS有限元仿真软件分析不同截面形状对螺旋桨的缠绕效果。从仿真结果可知，圆形纤维丝和矩形纤维丝对螺旋桨均有缠绕效果，但缠绕效果有所不同：1）对螺旋桨反作用力的影响，矩形截面纤维丝对其反作用力更大；2） 对螺旋桨旋转速度的影响，圆形截面纤维丝缠绕效能较优；3）对螺旋桨前行速度的影响，矩形截面纤维丝缠绕效能更优。