光纤陀螺热致漂移仿真分析及实验验证

佟向鹏

（海军驻北京地区第一军事代表室， 北京100854）

0 引言

光纤陀螺利用光纤线圈敏感角运动，在使用过程中会受到外界扰动因素的作用，从而影响陀螺的检测精度［1-3］，影响光纤陀螺性能的物理场包括温度、应力、磁场、辐照等［4］。为提高陀螺性能，研究人员从结构设计上降低每一种物理场的扰动，例如：用减震设计降低振动、冲击对光纤陀螺的影响，用铁镍合金材料对光纤环进行屏蔽以降低电磁场对光纤陀螺的影响等。在环境干扰诸因素中，温度变化是影响光纤陀螺输出信号精度的一个最重要因素［5］。光纤陀螺设计中，一般采用隔热材对光纤陀螺敏感线圈进行密封屏蔽的方法降低温度场对光纤陀螺的影响。然而，通过屏蔽方法完全避免温度场的影响是不可能的。为研制高精度光纤陀螺，必须在结构设计阶段对陀螺漂移进行估算。因此，对研究人员来说，使用准确的数学模型分析陀螺的热致漂移是迫切需要解决的问题。

在光纤陀螺中，温度对光纤环圈的影响可以分为两个方面。其一为温度的直接作用，主要因为光纤折射率对温度很敏感，从而导致环圈内部的非互易性。该热致漂移数学模型由Shupe首次提出［6］，模型考虑相向传播的光波相位差与石英光纤芯内温度变化速度的关系（热光效应），随后该模型被其他学者用于估计不同光纤缠绕方法下陀螺的漂移。其二为由温度诱导的应力作用，可看作是温度的二阶效应。在温度场作用下，光纤环圈各材料会产生热应力，热应力的存在引起了光纤长度及折射率的变化，从而改变光波的传输特性，该应力应变误差也是光纤陀螺温度误差的主要机理［7］。Mohr等［8］首次注意到应力应变对光纤陀螺漂移的影响，指出温度变化导致光纤中的弹性应变，从而给相位差带来附加的变化（弹光学效应）。Schadt［9］指出，由热光效应引起的漂移形状与由弹光性效应引起的漂移形状有很大的差别，它们的幅值与陀螺仪表内元件的几何形状和物理-机械特征有关。

本文对光纤陀螺热致漂移模型进行了深入探讨，在计算光纤陀螺热漂移时同时考虑了热光效应和热致弹光效应。随后，基于模型仿真计算并实验测试了环境温度变化下的陀螺漂移特性，实验结果与模型能较好地符合。

1 光纤中传输光的热致相位变化机理

保偏石英光纤由涂覆层、包层和纤芯组成，在光纤拉伸过程中形成应力场以保证在包层应力区两个相互正交的平面内产生折射系数的差别（双折射效应）。这样一来，该光纤就具有两个正交的极化平面：快速的XOZ平面和慢速的YOZ平面，光沿着其中一个平面传播。保偏光纤的结构如图1所示。

外界温度场变化对光纤中传输光相位的影响表现为两个方面，一是温度直接作用引起的光相位变化，二是热应力作用引起的光相位变化。

1.1 温度直接作用引起的光相位变化

如图1所示，光波在光纤芯内沿一个极化平面传播时，光相位可表示为

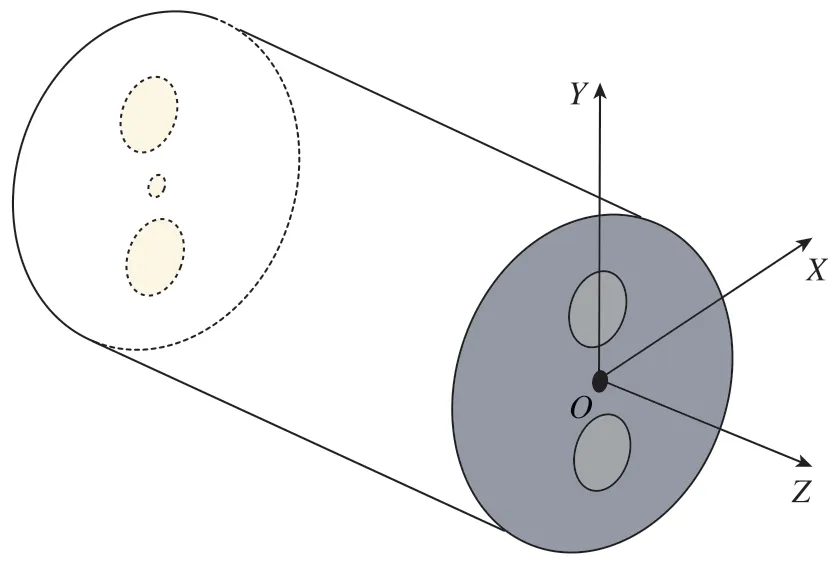
图1 保偏光纤结构示意图Fig.1 Structure diagram of polarization maintaining fiber

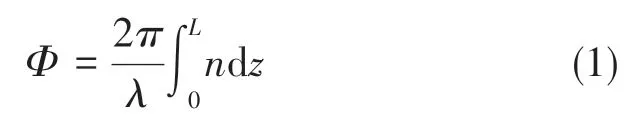
式（1）中，λ为光波波长，L为光纤长度，n为光纤折射率。

温度变化ΔT时，沿光纤传播的光波在温度场直接作用下引起的光相位变化可近似表示为［4，10-11］

1.2 热应力作用引起的光相位变化

光纤中纤芯、涂覆层、胶层材料均不同，这些材料具有不同的热膨胀系数。另外，受光纤陀螺结构限制，在任何温度场条件下，光纤环内部都会存在热应力，并且温度场变化时，光纤环内部热应力也会随之变化。

弹性应变Δε时，沿光纤传播的光波由应力变化引起的相位变化可表示为［12-13］

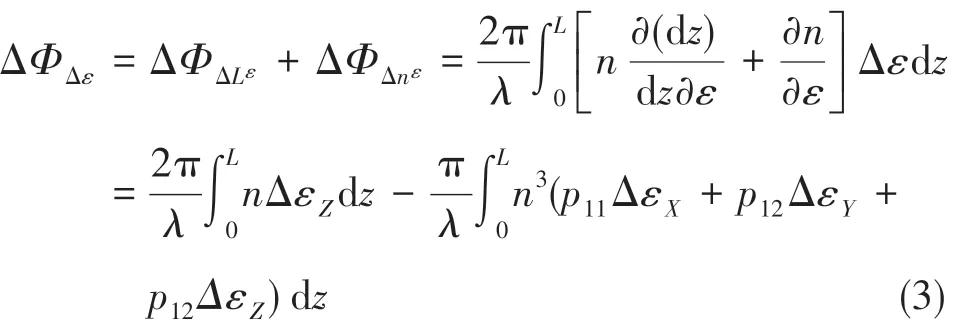
式（3）中，ΔΦΔLε为弹性应变作用下长度改变引起的光相位变化，ΔΦΔnε为弹性应变作用下折射率改变引起的光相位变化，p11、p12为光纤弹光系数，ΔεX、ΔεY、ΔεZ分别为光纤X轴、Y轴、Z轴方向上的微弹性应变。

2 光纤陀螺热致漂移模型及仿真研究

2.1 光纤陀螺热致漂移模型

考虑温度直接作用和热应力作用下的光相位变化，本文进一步推导光纤陀螺热致漂移模型。

根据目前中东等产油地区局势变化、国际原油市场价格走势，以及全球宏观经济形势发展和油气供需平衡等情况判断，年底前国际原油价格总体上将继续高位运行，波动幅度会较大，估计原油现货月均价可能在70美元/桶上下，涨势趋缓。近期，全球贸易摩擦继续升级，以及美国对伊朗的石油出口制裁日期临近，国际原油市场震荡将进一步加剧。

在Sagnac干涉仪中，假设光纤环长度为L，考虑距离光纤环一端z的一小段光纤dz，正反向传播的两束光波时间延迟为

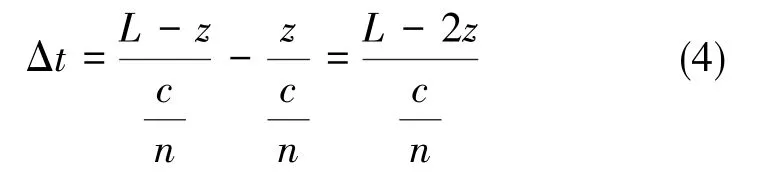
因此，在光束行程时间内的温度变化和弹性应变表示为

把式（5）带入式（2）、式（3）中，外界温度变化时热致总角速度可表示为

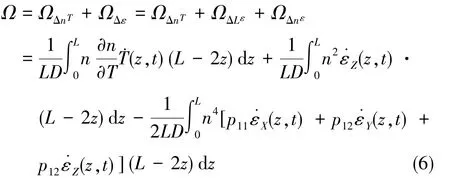
式（6）中，（z，t）为z处温度的时间导数，即温变速率；（z，t）、（z，t）、（z，t）分别为z处在X轴、Y轴、Z轴方向上弹性应变的时间导数；D为光纤环平均直径。

需要指出的是，包围光纤的涂覆层是可压缩的。在加热过程中，光纤截面上X轴和Y轴方向的应力σX和σY远小于Z轴方向的应力σZ。考虑到该边界条件，光纤上z处微应变可近似简化为，ν为泊松系数。则式（6）可简化为

由式（7）可知，根据光纤内参数温度变化率（z，t）及应变速率（z，t）的分布可计算出光纤陀螺的实时角速度。

2.2 光纤陀螺热致漂移仿真研究

为理论计算和实验测试光纤陀螺的热致漂移，本文设计实现了径向温度激励的无骨光纤环测试工装，如图2所示。

图2 光纤环测试工装Fig.2 Test fixture of fiber optical ring

无骨光纤环具有温度环境均匀、温度性能好等优点，是高精度光纤陀螺的首选光纤环。光纤环内外壁温度均可通过布置温度传感器测出，根据热量在均匀介质扩散的基本定律，可通过插值法计算出光纤环各个位置的温度信息。光纤环测试工装中，铝合金外骨架均匀粘贴加热片，用来提供稳定的热源。无骨光纤环外壁与铝合金外骨架距离1mm；光纤环上下盖用橡胶材料制成，对光纤环起支撑作用；光纤环外壁、空气、加热片间靠热对流传热。

仿真中，加热条件设置为：首先常温稳测1h，然后开启功率为3W的加热片，保持恒功率加热2h，之后关闭恒功率加热源，继续测试2h后结束。基于已知边界条件的光纤环内部温度建模方法，可得到5h内的光纤环内部温度分布，如图3所示。

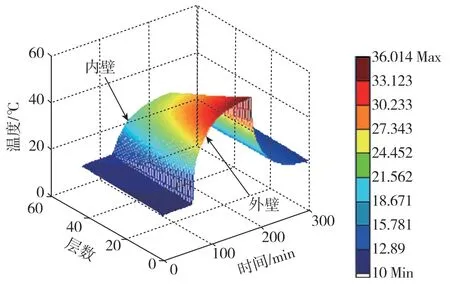
图3 光纤环内部温度分布Fig.3 Temperature distribution inside the fiber optical ring

图3中，外侧为光纤环外壁，即受热壁。可以看到，光纤环外壁相对于光纤环内壁有着更大的温变率。加热起始阶段的光纤环温变率较大，经测试瞬时温变率可达2℃/min，之后逐渐减小。关闭加热源后，保温起始阶段的光纤环温变率较大，之后逐渐减小。通过插值方法，求得该径向温度激励下的光纤环内部温度分布，然后根据每段光纤所在的空间位置，得到每段光纤的温度以及温度变化率，t）。

为得到环境温度变化下光纤环中的应力变化，建立了简化的力学模型，并采用弹性力学原理对模型进行应力分析。热应力仿真计算中，模型的主要参数设置如表1所示。

表1 仿真模型中的主要参数Table 1 Main parameters in simulation model

设置适当的边界条件，运用静力学求解器计算出5h实验过程中光纤Z轴方向的应力场分布，提取各t时刻计算得出的各点热应力值可计算得出应变速率（z，t）。之后，把温度变化率（z，t）及应变速率（z，t）带入式（7），可得到光纤陀螺热致角速度与时间的关系，如图4 所示。

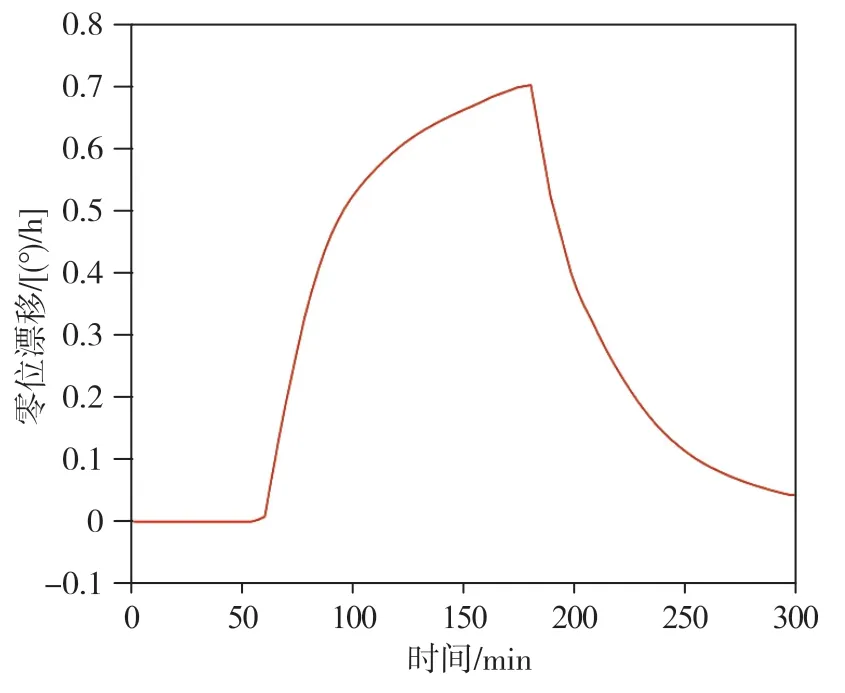
图4 热致漂移仿真曲线Fig.4 Simulation curve of thermal induced drift

由图4可知，整个热交换过程中，加热起始阶段陀螺的零偏变化较快，之后逐渐减慢。关闭加热源，保温起始阶段陀螺的零偏变化较快，之后逐渐减慢。仿真曲线的形状与图3中光纤环温度变化曲线的形状相似。

3 光纤陀螺热致漂移实验验证

为验证热致漂移模型的准确性，本文搭建了高精度光纤陀螺测试系统，如图5所示。测试系统包括：隔振地基、数据采集用计算机、陀螺信号处理电路和陀螺光学器件。光纤环测试工装位于隔热箱内，尽量减小外界环境因素对整个热交换测试过程的影响。

图5 光纤陀螺热致漂移测试系统Fig.5 Test system for thermal induced drift of FOG

实验中，选取3个光纤环依次安装在测试工装上，分别构成3个光纤陀螺系统FOG1、FOG2、FOG3。分别对3个陀螺系统设置与仿真过程相同的加热条件，扣除地球自转角速度分量后，热交换过程中各陀螺的零位变化如图6所示。

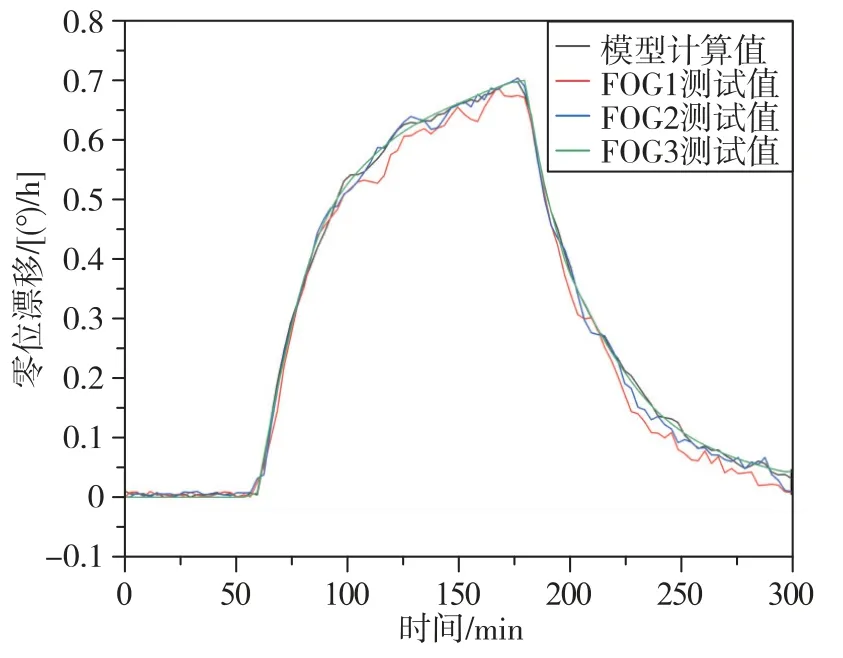
图6 光纤陀螺热致漂移测试结果Fig.6 Test results of FOG thermal induced drift

由图6可知，在整个热交换过程中，3个光纤陀螺零位变化趋势与仿真曲线能较好吻合。在加热起始阶段（60min～80min）及保温起始阶段（180min～200min），光纤环温度变化率较大，陀螺零偏测试值与模型计算值几乎完全重合。在加热持续阶段（80min～180min）及保温阶段（200min～300min），光纤环温变率逐渐减小，陀螺零偏测试值与模型计算值误差相对较大。为了定量评估热致漂移模型的可信度，使用式（8）计算热转换过程中零偏模型计算值与陀螺测试值之间的误差

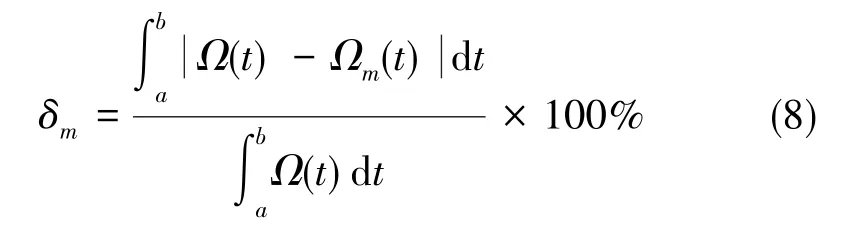
式（8）中，m为测试光纤陀螺的编号，Ω（t）为t时刻模型的计算值，Ωm（t）为t时刻的测试值，a为热交换实验起始时刻，b为热交换实验结束时刻。

热交换过程中（60min～300min），FOG1的测试值与模型计算值间的误差δ1为7.9%，FOG2的测试值与模型计算值间的误差δ2为2.8%，FOG3的测试值与模型计算值间的误差δ3为3.3%。由测试结果可知，热致漂移模型计算值与陀螺测试值之间的误差最大不超过8%，该模型能较好地反映陀螺实际热致漂移特性。

4 结论

为研制高精度光纤陀螺，需要在设计初始阶段对其热致漂移进行估算。因此，使用准确的数学模型分析陀螺的热致漂移特性是迫切需要解决的问题。本文考虑了光纤的热光效应和热致弹光效应，对光纤陀螺热致漂移模型进行了深入探讨。为验证模型准确性，基于模型理论计算并搭建了光纤陀螺系统，测试了环境温度变化下的陀螺漂移特性。测试结果表明，热致漂移模型零偏计算值与3只陀螺零偏测试值之间误差分别为7.9%、2.8%和3.3%，实验结果与模型能较好吻合。该研究成果对高精度光纤陀螺的设计具有重要指导意义。